فرادرسک م م یا کوچکترین مضرب مشترک چیست؟ — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
در آموزش‌های قبلی از مجموعه مطالب ریاضی مجله فرادرس، درباره تجزیه اعداد به عوامل اول بحث کردیم. بزرگترین مقسوم علیه مشترک یا ب م م و کوچکترین مضرب مشترک، از مباحث مهم و کاربردی برای تجزیه اعداد و ساده‌سازی کسرها هستند. در این آموزش از مجله فرادرس، مفهوم «کوچکترین مضرب مشترک» (Least Common Multiple) یا ک م م یا LCM و نحوه محاسبه آن را بررسی می‌کنیم.
مضرب چیست؟
اگر عددی را در یک عدد غیرصفر دیگر مانند 1، 2، 3، 4، 5 و... ضرب کنیم، مضرب آن به دست می‌آید.
برای مثال، مضارب اعداد ۴ و ۵ به‌صورت زیر هستند:
مضرب مشترک چیست؟
مضرب مشترک دو یا چند عدد، مضاربی هستند که بین آن اعداد مشترک باشند. در قسمت قبل، مضارب اعداد ۴ و ۵ را نوشتیم. مضارب مشترک این دو عدد، در زیر مشخص شده‌اند:
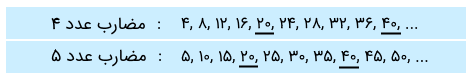
همان‌طور که می‌بینیم، اعداد ۲0، 40، 60 و... مضارب مشترک این دو عدد هستند.
کوچکترین مضرب مشترک چیست؟
ساده‌ترین راه برای محاسبه کوچکترین مضرب مشترک، نوشتن مضارب مشترک و انتخاب کوچکترین آن‌ها است. ک م م - همان‌گونه که از نامش پیداست - کوچکترین مضربی است که بین اعداد مورد نظر مشترک باشد. مثلاً برای اعداد ۴ و ۵ که در بالا به آن اشاره شد، اگر بخواهیم کوچکترین مضرب مشترک را از بین مضارب مشترک ۲0، 40، 60 و... تعیین کنیم، عدد 20 را در نظر می‌گیریم که از همه مضارب مشترک کوچکتر است.
روش اول یافتن ک م م
در روش اول برای یافتن کوچکترین مضرب مشترک چند عدد مختلف، ابتدا مضارب آن‌ها را از کوچک به بزرگ مینویسیم و اولین مضربی را که برای همه اعداد مشترک است، به عنوان کوچکترین مضرب مشترک مشخص می‌کنیم.
مثال ۱
ابتدا با مثال ساده یافتن کوچکترین مضرب مشترک دو عدد ۳ و ۵ شروع می‌کنیم. برای یافتن ک م م، مضارب هریک از این اعداد را مینویسیم:
- مضارب عدد ۳، اعداد ۳، ۶، ۹، 12، 15، 18 و... هستند.
- مضارب عدد 5، اعداد ۵، 10، 15، 20، 25 و... هستند.
از بین مضارب بالا، مضارب مشترک و کوچکترین آن‌ها را انتخاب می‌کنیم.
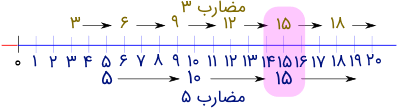
بنابراین، عدد ۱۵ کوچکترین مضرب مشترک اعداد ۳ و ۵ است.
مثال ۲
کوچکترین مضرب مشترک دو عدد ۴ و ۱۰ را به‌دست آورید.
مضارب هر دو عدد را به صورت زیر مینویسیم:
- مضرب‌های ۴: ۴، 8، 12، 16، 20 و...
- مضرب‌های 10: 10، 20، 30، 40 و...
همان‌طور که می‌بینیم، 20 اولین مضربی از دو عدد است که مشترک است.
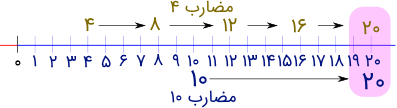
بنابراین، کوچکترین مضرب مشترک اعداد 4 و 10، عدد 20 است.
مثال ۳
می‌خواهیم کوچکترین مضرب مشترک دو عدد 6 و 15 را به دست آوریم. ابتدا مضارب هر دو عدد را به صورت زیر مینویسیم:
- مضارب ۶: 6، 12، 18، 24، 30 و...
- مضارب 15: 15، 30، 45، 60 و...
همان‌طور که می‌بینیم، اولین یا به عبارت بهتر، کوچکترین عددی که مضارب دو عدد در آن مشترک و برابر هستند، 30 است. بنابراین، ک م م دو عدد 6 و 15، عدد 30 است.
مثال ۴
در این مثال، به جای تعیین ک م م دو عدد، می‌خواهیم ک م م سه عدد ۴، ۶ و ۸ را محاسبه کنیم. برای انجام این کار، دقیقاً مشابه حالتی عمل می‌کنیم که دو عدد داریم. مانند مثال‌های قبل، ابتدا مضارب سه عدد را مینویسیم:
- مضارب عدد 4: ۴، 8، 12، 16، 20، 24، 28، 32، 36 و...
- مضارب عدد 6: ۶، 12، 18، 24، 30، 36 و...
- مضارب عدد 8: 8، 16، 24، 32، 40 و...
همان‌طور که می‌بینیم، عدد ۲۴، کوچکترین مضرب مشترک بین سه عدد است.
روش دوم یافتن ک م م
یک راه دیگر برای یافتن ک م م بین چند عدد، استفاده از عوامل اول آن‌ها است. در آموزش‌های قبلی، درباره تجزیه اعداد به عوامل اول بحث کردیم. برای درک بهتر روش دوم، آن را با یک مثال بیان می‌کنیم.
فرض کنید می‌خواهیم ک م م دو عدد ۱۲ و ۱۸ را به دست آوریم. در گام اول، دو عدد را به عوامل اول تجزیه می‌کنیم:
و
3 × ۳ × 2 = ۱۸
عوامل اول را به گونه‌ای می‌چینیم تا آن‌هایی که برابر هستند به صورت عمودی با هم منطبق شوند:
3 × 2 × 2 = 12
3 × 3 × 2 = ۱۸
اکنون عوامل اول هر ستون را مینویسیم و در یکدیگر ضرب می‌کنیم. توجه کنید که اگر عاملی در یک ستون چند بار تکرار شده باشد، آن را یک بار مینویسیم. بنابراین، داریم:
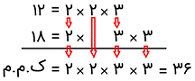
برای بیش از دو عدد نیز به همین صورت عمل کرده و به سادگی، کوچکترین مضرب مشترک را محاسبه می‌کنیم.
مثال ۵
می‌خواهیم با استفاده از تجزیه به عوامل اول، ک م م دو عدد ۱۵ و ۱۸ را محاسبه کنیم.
با توجه به روشی که گفته شد، عوامل اول دو عدد را به صورت زیر نوشته و ک م م را به دست می‌آوریم:
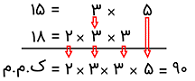
بنابرین، کوچکترین مضرب مشترک دو عدد ۱۵ و ۱۸، عدد ۹۰ است.
آزمون سنجش یادگیری ک م م
در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث ک م م را با طرح سوال‌های چندگزینه‌ای می‌سنجیم. پس از جواب دادن به تمام سوال‌ها، نتیجه آزمون برای شما به نمایش درمی‌آید.
کوچکترین مضرب مشترک بین اعداد 6 و 8 چیست؟
12
16
24
48
برای به دست آوردن کوچکترین مضرب مشترک یا همان ک م م دو عدد، ابتدا مضارب آن‌ها را تا ظاهر شدن اولین عدد مشترک مینویسیم. مضارب اعداد 6 و 8 عبارت هستند از:
- مضارب عدد 6: 6، 12، 18، 24، 30، ...
- مضارب عدد 8: 8، 16، 24، 32، ...
عدد 24، کوچکترین مضرب مشترک بین اعداد 6 و 8 است.
کوچکترین عدد بخش‌پذیر بر اعداد 9 و 12 چیست؟
36
45
60
72
کوچکترین عدد بخش‌پذیر بر چند عدد، همان کوچکترین مضرب مشترک یا ک م م آن‌ها است. بنابراین، برای به دست آوردن این عدد، مضارب اعداد را تا ظاهر شدن اولین عدد مشترک مینویسیم. مضارب اعداد 9 و 12 عبارت هستند از:
- مضارب عدد 9: 9، 18، 27، 36، 45، ...
- مضارب عدد 12: 12، 24، 36، 48، ...
عدد 36، کوچکترین مضرب مشترک بین اعداد 9 و 12 است.
ک م م اعداد 6، 8 و 9 کدام گزینه است؟
48
60
63
72
برای به دست آوردن ک م م سه عدد 6، 8 و 9، مضارب آن‌ها را مینویسیم:
- مضارب عدد 6: 6، 12، 18، 24، 30، 36، 42، 48، 54، 60، 66، 72، 78، ...
- مضارب عدد 8: 8، 16، 24، 32، 40، 48، 56، 64، 72، 80، ...
- مضارب 9: 9، 18، 27، 36، 45، 54، 63، 72، 81، ...
عدد 72، کوچکترین مضرب مشترک اعداد 6، 8 و 9 است.
کدامیک از گزینه‌های زیر، ک م م سه عدد 12، 15 و 18 را نمایش می‌دهد؟
108
144
180
216
به منظور تعیین ک م م اعداد 12، 15 و 18، مضارب آن‌ها را مینویسیم:
- مضارب 12: 12، 14، 24، 36، 48، 60، 72، 84، 96، 108، 120، 132، 144، 156، 168، 180، 192، ...
- مضارب 15: 15، 30، 45، 60، 75، 90، 105، 120، 135، 150، 165، 180، 195، ...
- مضارب 18: 18، 36، 54، 72، 90، 108، 126، 144، 162، 180، 198، ...
بنابراین، کوچکترین مضرب مشترک اعداد 12، 15 و 18، برابر با عدد 180 است.
کوچکترین مضرب مشترک اعداد 6، 9، 10 و 15 چه می‌شود؟
90
72
60
180
فیلم های آموزش ک م م یا کوچکترین مضرب مشترک چیست؟ — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
فیلم آموزشی مفهوم مضرب و مضرب مشترک
فیلم آموزشی روش اول یافتن ک م م
فیلم آموزشی روش دوم یافتن ک م م
عالی . عالی . توضیحات عالیب
عالی با این روش که گذاشتید راحت ک.م.م دو عدد را پیدا می کنم.
راحت ترین راه برای ب دست اوردن ک م م:
دو عدد رو در هم ضرب کنید سپس بر ب م م تقسیم کنید. به همین راحتی ک م م به دست میاد
سلام میخواستم بدونم که چجوری میتونم ک.م.م و ب.م.م ۶ تا عدد رو پیدا کنم
سلام کافیه همشون رو به عوامل اول تبدیل کنید و بعد برای ک م م باید همه اعداد رو در هم ضرب کنیو البته در قسمت عوامل اول مشترک باید اونی که بیشترین توان رو داره استفاده کنید بیاید با هم یه مثال بزنیم :
ک م م اعداد : ۱۴ ، ۷ ، ۳۲ ، ۱۲ ، ۹ ، ۱۰ را به دست بیاورید :
اول به عوامل اول تجزیه می‌کنیم :
۱۴ = ۲×۷
۷ = ۷
۳۲ = ۲×۲×۲×۲×۲
۱۲ = ۳×۲×۲
۹=۳×۳
۱۰=۲×۵
خب حالا برای ک م م باید عوامل اولی که مشترک هستند رو با توان بالاتر پیدا کنیم و ضرب در عواملی کنیم که مشترک نیستند از اونجایی که هیچ کدام از عوامل اولی که بعد از تجزیه اعداد فوق به دست آوردیم در همه اعداد مشترک نیستند پس ک م م این اعداد میشه ضرب تمام عوامل غیر مشترک که میشه: ۷×۳×۲×۵ = ۲۱۰ و اما برای ب م م باید عوامل مشترک رو با هم ضرب کنی از اونجایی عامل مشترکی وجود نداره پس ب م م هم برای این اعداد تعریف نمیشه
بسیار عالی بود ممنون مشکلم بر طرف شد
با تشکر اقای حمیدی
عالی بود ولی برای پیدا کردن ک م م چند تا روش دیگه هم هست اگه ممکنه اونا رو هم قرار بدید.
خیلی عالی بود ممنون.
عالی بود استاد
سلام خیلی ممنون از توضیحات خوب شما
اینجوری که اینجا گفته اشتباهه ک.م.م اعداد 15و 18 سه هست که در اینجا گفته 90
سلام.
عدد ۳ بزرگترین مقسوم‌علیه مشترک یا همان ب.م.م. دو عدد ۱۵ و ۱۸ است.
موفق باشید.
سلام و سپاس از همراهی‌تان با مجله فرادرس.
شاد باشید.
بسیار عالی و مفید
سلام من چجوری ک.م.م و ب.م.م چند تا عدد مثل ک.م.م عدد های 34 _67_87_84_25_65_65 رو بدست بیارم
سلام.
سپاس از همراهی‌تان با مجله فرادرس.
شاد و پیروز باشید.
واقعا عالی بود، خیلی خوب ب م م رو یاد گرفتم ممنون از شما آقای حمیدی .
عالی و مفید بود ممنونم??❤
سلام محمد عزیز.
سپاس از همراهی‌تان با مجله فرادرس.
شاد و پیروز باشید.
سلام.
خوشحالیم که این آموزش برایتان مفید بوده است.
سالم و شاد باشید.
خیلی متشکرم بابت مطالب و توضیحات ، ممنون از شما آقای حمیدی .
از شما خیلی ممنونم
خیلی خوب
خیلی عالی بود با تشکر از شما
عالی بود خیلی بهم کمک کرد
سلام پارسای عزیز.
از اینکه این آموزش برایتان مفید بوده، بسیار خوشحالیم.
سالم و سربلند باشید.
خیلی عالی بود ممنون
سلام.
خوشحالیم که این آموزش برایتان مفید بوده است.
سپاس از همراهی‌تان.
باید عارض بشم که در مضرب های 5و4 ک در اول ذکر شده
در مضرت 4 شما 38 رو اشتباه حساب کردید چون 38 کی مضرب 4 هستش؟
آیا ک م م عدد 15و 10
30,می شود
سلام.
اشتباه تایپی اصلاح شد.
از همراهی و بازخورد شما سپاسگزاریم.
سلام.خیلی ممنون از سایت خوبتون.
من یه سوال داشتم.ک.م.م رو باید بزاریم توی پرانتز یا توی کروشه
ک.م.م توی کروشه [ ]
ب.م.م توی پرانتز ()
سلام خسته نباشید
ک م م 1396و1397 رو میشه بگید
خب عزیز من ما گفتیم که دو عدد متوالی پشت سر هم ک.م.م میشه 1 این یه قانون هس
میشه حاصل ضربشون
خب ببین چون اعداد متولی هستن ب م م شون میشه 1
و
ک م م شون هم میشه ضربشون
عالیه???
واقعااا ممنونم از سایت خوبتون من ب.م.م و ک.م.م را خیللی خوب یاد گرفتم.
ممنون از زحمات شما
بسیار عالی بود اما میشه گویندتون رو عوض کنید سرم درد گرفت
فوق العاده بود ممنون از زحمات شما
برای ک.م.م کسر ها پاسخ alireza
به نظر من باید اول مضرباشو به دست بیاریم بعد هرکدوم از مضارب شبیه هم بودن رو مینویسیم البته ساده کردن کسر رو هم باید در نظر بگیریم
عالی عالی هست
سلام خسته نباشید عالی بود فقط یه سوال برای ک.م.م گرفتن چندتا
اعداد کسری چجوری باید عمل کنیم؟
درود و بسیار عالی
سلام
خسته نباشید ممنون از تدریس عالی و دقیق و کوتاه شما من اصلا ک م م و ب م م رو متوجه نشدم ولی الان خوب یاد گرفتم
مرسی واقعا ❤️
خیلی ممنون.هیچ کاری بهتر از کمک کردن به مردم اونم به صورت رایگان نیست.
درسته??
عالی
ممنون از فرادرس بهترین سایت آموزشی اینه
عالی بود
خیلی برام مفید بود
مرسی?
عالی،ممنون.
بسیاررررررررررررررررررررررررررررررررررررر عااااااااااااااااااااالی
عالی بود مرسی
عالی
عالیههههههههههههههههههههههههه ممنون
ولی روش نرده بانی هم هست من یادم رفته بود چطوری باید حلش کنم تا آخر دیدم ولی نبود
ولی عالیییی و دقیق گفتی درود بر تو
سلام خسته نباشید ممنون از شیوه بیانتون فوق العاده قابل فهم بود