تانژانت چیست و چگونه بدست می آید؟ + جدول تانژانت تمام زاویه ها

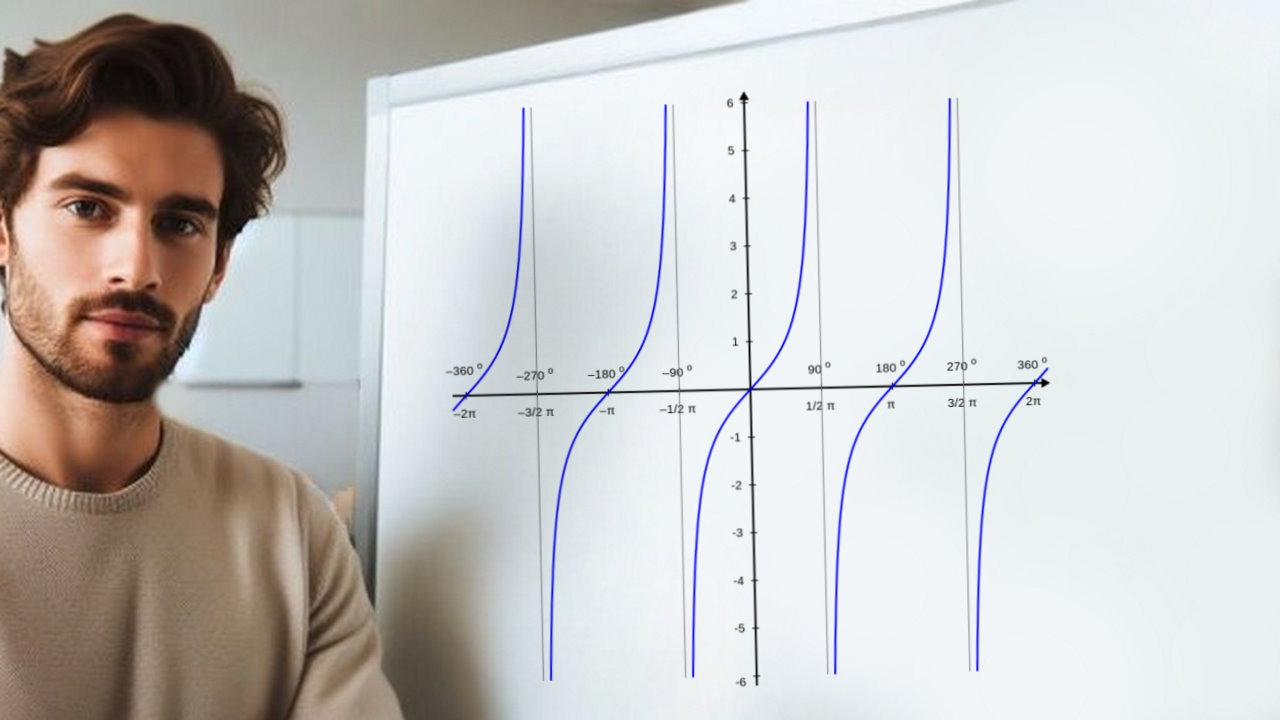
تانژانت یکی از توابع نسبت‌های اصلی مثلثاتی است و یک تابع بسیار رایج در مثلثات است. تابع تانژانت را می‌توان به صورت نسبت تابع سینوس و تابع کسینوس بیان کرد. در یک مثلث قائم‌الزاویه، فرمول تابع تانژانت به‌صورت نسبت ضلع مقابل به زاویه بر ضلع مجاور بیان می‌شود. همچنین می‌توان آن را به‌عنوان متقابل تابع کتانژانت بیان کرد. از نظر ریاضی، تابع تانژانت به صورت $$f(x) = \tan x $$ نوشته می‌شود. در این آموزش، به این پرسش پاسخ می‌دهیم که تانژانت چیست و با  نمودار تابع تانژانت، دامنه و برد آن، اتحادهای مثلثاتی تانژانت و... آشنا می‌شویم. همچنین چند مثال مربوط به تابع تانژانت را برای درک بهتر مفهوم آن حل خواهیم کرد.

تانژانت چیست ؟

تانژانت در اصل معادل کلمه فرانسوی tangente است.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

طبق تعریف، اگر زاویه‌ای در نظر بگیریم که رأس آن در مبدأ یک دستگاه مختصات قائم در صفحه و ضلع اول آن منطبق بر قسمت مثبت محور $$x$$ باشد، تانژانت آن زاویه عبارت است از عرض هر نقطه واقع بر ضلع دوم زاویه به‌جز رأس، تقسیم بر طولِ ناصفر آن نقطه.

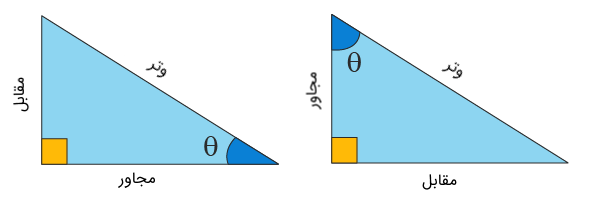
برای درک بهتر مفهوم تانژانت، ابتدا باید ببینیم منظور از ضلع مقابل و مجاور چیست. وقتی می‌گوییم ضلع مقابل، منظورمان آن ضلعی است که روبه‌روی زاویه مورد نظر قرار دارد و ضلعی غیر از وتر و ضلع دیگر تشکیل‌دهنده زاویه است. منظور از ضلع مجاور نیز آن ضلعی است که در کنار وتر زاویه مورد نظر را تشکیل می‌دهد. شکل زیر، اضلاع مقابل و مجاور را برای زاویه $$ \theta$$ در دو حالت مختلف نشان می‌دهد.

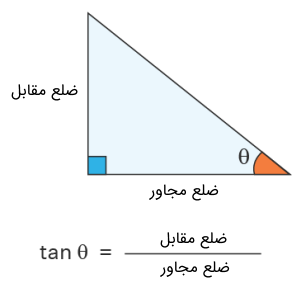
همان‌طور که گفتیم، تانژانت یک زاویه، با نسبت زاویه مقابل به زاویه مجاور آن زاویه تعریف می‌شود. شکل زیر این موضوع را به‌خوبی نشان می‌دهد.

دایره مثلثاتی و تانژانت

دایره مثلثاتی دایره‌ای است که مرکز آن روی مبدأ دستگاه مختصات و شعاع آن برابر با واحد (یک) است. زاویه‌های مختلف، از ۰ تا ۳۶۰ درجه، را می‌توان به‌سادگی روی محیط این دایره مشخص کرد. بدین صورت که یک نقطه را روی محیط دایره انتخاب می‌کنیم، سپس آن نقطه را به مبدأ مختصات وصل می‌کنیم. همچنین، یک عمود به محور افقی از آن نقطه رسم می‌کنیم. شکل زیر این موضوع را به‌خوبی نشان می‌دهد. تانژانت زاویه $$\theta $$ در شکل زیر، برابر خوهد بود با:

$$\large \tan \theta = \frac y x $$

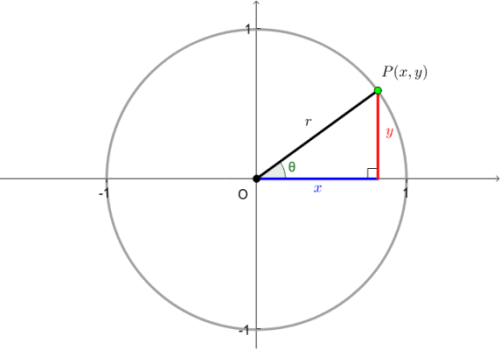
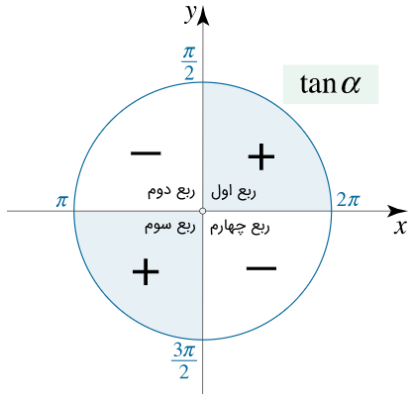
بسته به اینکه نقطه در کدام ربع باشد، تانژانت می‌تواند منفی یا مثبت شود. وقتی یکی از دو پارامتر $$x$$ و $$y$$ منفی باشند، آنگاه تانژانت نیز منفی خواهد بود. زیرا تانژانت برابر با نسبت $$ \frac y  x $$ است. شکل زیر نشان می‌دهد که تانژانت در کدام ربع‌ها مثبت و در کدام ربع‌ها منفی است.

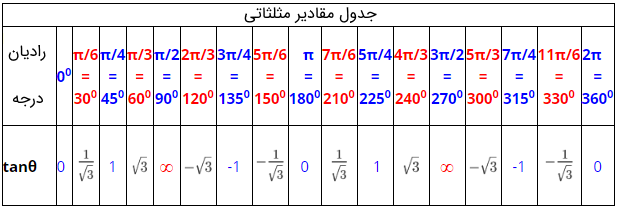
جدول تانژانت زاویه ها

برخی از زاویه‌های خاص هستند که از بر بودن تانژانت آن‌ها در بسیاری از مواقع که با مسائل ریاضی سر و کار داریم، کارساز خواهد بود. این زاویه‌ها ۰، ۳۰، ۴۵، ۶۰، ۹۰ و... هستند که در جدول زیر آورده شده‌اند.

رسم تابع تانژانت

دوره تناوب تابع تانژانت $$\pi$$ است، زیرا نمودار در فواصل $$kpi$$ که $$k$$ عددی ثابت است تکرار می‌شود. اگر تابع تانژانت از $$ − \frac { \pi } { 2 } $$ تا $$  \frac { \pi } { 2 } $$ را رسم کنیم، می‌توانیم رفتار آن را در یک دوره کامل ببینیم. اگر به هر بازه بزرگ‌تری نگاه کنیم، خواهیم دید که ویژگی‌های نمودار تکرار می‌شوند.

می‌توانیم رفتار گرافیکی تابع تانژانت را با بررسی مقادیر برخی از زوایای خاص، همان‌طور که در جدول بالا فهرست شده است، تحلیل کنیم. برای مثال، در نقطه $$x = \frac \pi 3 = \frac {3.14}{3} = 1.046$$ مقدار تابع برابر است با $$\sqrt 3 = 1.7 $$. دقت کنید که برای محاسبه، $$\pi $$ را همان مقدار معروف $$3.14$$ درنظر بگیرید.

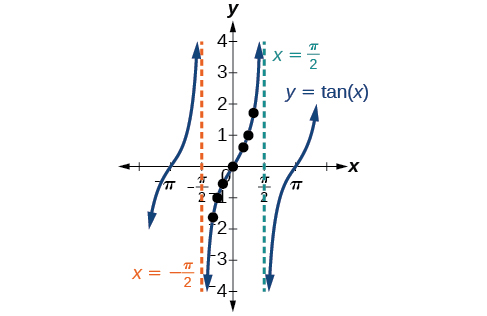
تابع تانژانت در نقاط $$x=\frac{(2k+1)\pi}{2}$$ دارای مجانب قائم است. یعنی تابع در این نقاط تعریف‌نشده است. برای آشنایی بیشتر با مجانب، به آموزش «مجانب تابع — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.

تانژانت فرد است یا زوج؟

با استفاده از تعریف تانژانت می‌توانیم تعیین کنیم که آیا تانژانت یک تابع فرد است یا زوج:

$$ \large \tan (-x ) = \frac {\sin (-x)}{\cos (-x)}=\frac {-sin x}{\cos x} = -frac{\sin x }{\cos x} =-tan x $$

بنابراین، تانژانت یک تابع فرد است.

این نکات به ما کمک می‌کنند تا نمودار را ترسیم کنیم، اما باید تعیین کنیم که نمودار در جایی که تعریف نشده است چگونه رفتار می‌کند.

دامنه و برد تابع تانژانت

همان‌طور که دیدیم، تابع تانژانت در مضرب‌های فرد $$ \frac \pi 2 $$ تعریف نمی‌شود، زیرا طبق تعریف هندسی، در این حالت، طول قاعده مثلث قائم الزاویه یا همتن ضلع مجاور صفر است و تعریف عدد بر صفر تعریف‌نشده است. بنابراین، دامنه $$\tan x $$ همه اعداد حقیقی هستند، جز مضرب‌های فرد $$\frac \pi 2 $$. اما، برد تابع تانژانت شامل تمام اعداد حقیقی است، زیرا مقدار $$\tan x $$ از منفی بی‌نهایت تا مثبت بی‌نهایت تغییر می‌کند. نمودر تانژانت نیز این موضوع را به‌خوبی نشان می‌دهد.

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

بنابراین، به‌طور خلاصه، می‌توان گفت:

• دامنه تابع تانژانت $$\mathbb{R} - {\frac{(2k+1)\pi}{2}}$$ است که در آن، $$k$$ یک عدد صحیح است.
• برد تابع تانژانت $$\mathbb{R}$$ است که در آن $$\mathbb{R}$$ مجموعه اعداد حقیقی است.

برای آشنایی بیشتر با دامنه و برد، به آموزش «دامنه و برد تابع — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.

مشتق تابع تانژانت

از آنجا که تابع تانژانت برابر با نسبت سینوس به کسینوس است، با استفاده از قاعده خارج قسمت به سادگی می‌توان مشتق آن را به دست آورد:‌

$$ \large \begin {align*} \left ( { \tan x } \right ) ^ \prime &\; = { { \left ( { \frac { {  \sin x }  } { { \cos x } }  } \right ) ^ \prime } } = { \frac { { { {  \left (  { \sin x }  \right ) } ^  \prime } \cos x – \sin x { {  \left (  { \cos x } \right ) } ^ \prime } } } {  { { {  \cos } ^ 2 }  x } }  } \ &\; = { \frac { { \cos x \cdot \cos x – \sin x \cdot \left ( { – \sin x }  \right ) } } {  { {  { \cos } ^ 2  } x }  }  } = { \frac { { { {  \cos } ^ 2 }  x + { { \sin }  ^  2 } x } } {    { {  { \cos } ^  2 } x } }   } = { \frac { 1  } { {  { {  \cos } ^ 2 } x } } . }  \end {align*} $$

فرمول‌های تانژانت

فرمول‌های تانژانت را می‌توان از فرمول‌های مشابه شامل سینوس و کسینوس استخراج کرد. در ادامه، مهم‌ترین این فرمول‌ها را معرفی می‌کنیم.

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

فرمول تانژانت جمع دو زاویه

فرمول تانژانت جمع دو زاویه به‌صورت زیر بیان می‌شود:

$$ \large
\begin {aligned}
\tan ( \alpha + \beta ) &\; = \frac { \sin ( \alpha + \beta ) } { \cos ( \alpha + \beta ) } \
&\; = \frac { \sin \alpha \cos \beta + \cos \alpha \sin \beta } { \cos \alpha \cos \beta-sin \alpha \sin \beta } \
&\; = \frac { \frac { \sin \alpha \cos \beta } { \cos \alpha \cos \beta } + \frac { \cos \alpha \sin \beta } { \cos \alpha \cos \beta } } { \frac { \cos \alpha \cos \beta } { \cos \alpha \cos \beta } -frac { \sin \alpha \sin \beta } { \cos \alpha \cos \beta } } \
&\; = \frac { \tan \alpha + \tan \beta } { 1 - \tan \alpha \tan \beta }
\end {aligned} $$

فرمول تانژانت تفاضل دو زاویه

برای تعیین فرمول تانژانت اختلاف دو زاویه، می‌توانیم از تساوی $$\tan (-beta) = - \tan (\beta)$$ استفاده کنیم:

$$ \large \begin {aligned}
&\; \tan ( \alpha - \beta ) = \tan [ \alpha + ( - \beta ) ] \
&\; \tan ( \alpha - \beta ) = \frac { \tan \alpha + \tan ( - \beta ) } { 1 - \tan \alpha \tan ( - \beta ) } \
&\; \tan ( \alpha - \beta ) = \frac { \tan \alpha - \tan \beta } { 1 + \tan \alpha \tan \beta }
\end {aligned} $$

فرمول تانژانت دو برابر زاویه

تانژانت دو برابر زاویه را می‌توان با استفاده از فرمول تانژانت مجموع دو زاویه به‌دست آورد:

$$ \large \begin {aligned}
&\; \tan ( 2 \alpha ) = \tan ( \alpha + \alpha ) \
&\; \tan ( 2 \alpha ) = \frac { \tan \alpha + \tan \alpha } { 1 - \tan \alpha \tan \alpha } \
&\; \tan ( 2 \alpha ) = \frac { 2 \tan \alpha } { 1 - \tan ^ { 2 } \alpha }
\end {aligned}
$$

فرمول تانژانت نصف زاویه

تانژانت نیم‌زاویه را می‌توان به سه شکل مختلف زیر نوشت:

$$ \large \begin {aligned}
&\; \tan \frac { \alpha } { 2 } = \pm \sqrt { \frac { 1 - \cos \alpha }{ 1 + \cos \alpha } } \
&\; \tan \frac { \alpha } { 2 } = \frac { \sin \alpha } { 1 + \cos \alpha } \
&\; \tan \frac { \alpha } { 2 } = \frac { 1 - \cos \alpha } { \sin \alpha }
\end {aligned}
$$

در شکل اول، علامت توسط ربعی که زاویه $$\frac \alpha 2 $$ در آن قرار دارد تعیین می‌شود.

مثال‌های تانژانت

در این بخش، مثال‌های متنوعی را درباره تانژنت حل می‌کنیم.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

مثال اول تانژانت

تساوی زیر را اثبات کنید:

$$ \large \tan \frac { \alpha } { 2 } = \pm \sqrt { \frac { 1 - \cos \alpha } { 1 + \cos \alpha } } $$

حل: از تعریف تانژانت استفاده می‌کنیم و خواهیم داشت:‌

$$ \large \begin {aligned}
\tan \frac { \alpha } { 2 } = &\; \frac { \sin \frac { \alpha }{ 2 } } { \cos \frac { \alpha } { 2 } } \
\tan \frac { \alpha } { 2 } = &\; \frac { \pm \sqrt { \frac { 1 - \cos \alpha } { 2 } } } { \pm \sqrt { \frac { 1 + \cos \alpha } { 2 } } } \
\tan \frac { \alpha } { 2 } = &\; \pm \frac { \sqrt { 1 - \cos \alpha } } { \sqrt { 1+ \cos \alpha } } \
\end {aligned} $$

مثال دوم تانژانت

تساوی $$ \tan (\alpha/2) = (1 − \cos \alpha)/sin \alpha $$ را اثبات کنید.

حل: از تعریف تانژانت کمک می‌گیریم و داریم:

$$ \large \begin {aligned}
&\; \tan \frac { \alpha } { 2 } = \frac { \sin \frac { \alpha } { 2 } } { \cos \frac { \alpha } { 2 } } \
&\; \tan \frac { \alpha } { 2 } = \left ( \frac { \sin \frac { \alpha }{ 2 } } { \cos \frac { \alpha } { 2 } } \right ) \left ( \frac { 2 \sin \frac { \alpha } { 2 } } { 2 \sin \frac { \alpha } { 2 } } \right ) \
&\; \tan \frac { \alpha } { 2 } = \frac { 2 \sin ^ { 2 } \frac { \alpha } { 2 } } { 2 \sin \frac { \alpha } { 2 } \cos \frac { \alpha } { 2 } } \
&\; \tan \frac { \alpha } { 2 } = \frac { 2 \left ( \frac { 1 - \cos \alpha } { 2 } \right ) } { \sin 2 \frac { \alpha } { 2 } } \
&\; \tan \frac { \alpha } { 2 } = \frac { 1 - \cos \alpha } { \sin \alpha }
\end {aligned}
$$

مثال سوم تانژانت

تساوی $$ \tan (\alpha − 2) = \sin \pi/(1 + \cos \alpha) $$ را اثبات کنید.

حل: از مثال قبل کمک می‌گیریم و می‌نویسیم:

$$ \large \begin {aligned}
&\; \tan \frac { \alpha } { 2 } = \frac { 1 - \cos \alpha } { \sin \alpha } \
&\; \tan \frac { \alpha } { 2 } = \left ( \frac { 1 - \cos \alpha }{ \sin \alpha } \right ) \left ( \frac { 1 + \cos \alpha } { 1 + \cos \alpha } \right ) \
&\; \tan \frac { \alpha } { 2 } = \frac { 1 - \cos ^ { 2 } \alpha }{ ( \sin \alpha ) ( 1 + \cos \alpha ) } \
&\; \tan \frac { \alpha } { 2 } = \frac { \sin ^ { 2 } \alpha } { ( \sin \alpha ) ( 1 + \cos \alpha ) } \
&\; \tan \frac { \alpha } { 2 } = \frac { \sin \alpha } { 1 + \cos \alpha }
\end {aligned} $$

مثال چهارم تانژانت

با استفاده از تانژانت نیم‌زاویه مقدار دقیق $$ \tan 15^circ $$ را پیدا کنید.

حل: این مقدار را می‌توانیم به دو صورت به‌دست آوریم.

روش اول:

$$ \large \begin {aligned}
&\; \tan 15 ^ { \circ } = \tan \frac { 30 ^ { \circ } } { 2 } \
&\; \tan 15 ^ { \circ } = \frac { 1 - \cos 30 ^ { \circ } } { \sin 30 ^ { \circ } } \
&\; \tan 15 ^ { \circ } = \frac { \left ( 1 - \frac { \sqrt { 3 } } { 2 } \right ) } { \left ( \frac { 1 } { 2 } \right ) } \
&\; \tan 15 ^ { \circ } = \left ( \frac { 2 + \sqrt { 3 } }{ 2 } \right ) \left ( \frac { 2 } { 1 } \right ) \
&\; \tan 15 ^ { \circ } = 2 - \sqrt { 3 }
\end {aligned} $$

روش دوم:

$$ \large \begin {aligned}
&\; \tan 15 ^ { \circ } = \tan \frac { 30 ^ { \circ } } { 2 } \
&\; \tan 15 ^ { \circ } = \frac { \sin 30 ^ { \circ } } { 1 + \cos 30 ^ { \circ } } \
&\; \tan 15 ^ { \circ } = \frac { \left ( \frac { 1} { 2 } \right ) }{ \left ( 1 + \frac { \sqrt { 3 } } { 2 } \right ) } \
&\; \tan 15 ^ { \circ } = \left ( \frac { 1 } { 2 } \right ) \left ( \frac { 2 } { 2 + \sqrt { 3 } } \right ) \
&\; \tan 15 ^ { \circ } = \frac {1 } { 2 + \sqrt { 3 } } \
&\; \tan 15 ^ { \circ } = \left ( \frac { 1 }{ 2 + \sqrt { 3 } } \right ) \left ( \frac { 2 - \sqrt { 3 } } { 2 - \sqrt { 3 } } \right ) \
&\; \tan 15 ^ { \circ } = 2 - \sqrt { 3 }
\end {aligned} $$

مثال پنجم تانژانت

مقدار دقیق زاویه $$75 ^circ $$ را تعیین کنید.

حل: از آنجا که $$75^circ = 45^ \circ + 30 ^ \circ $$، خواهیم داشت:

$$ \large \begin {aligned}
&\; \tan 75 ^ { \circ } = \frac { \tan 45 ^ { \circ } + \tan 3 0 ^ { \circ } } { 1 - \tan 45 ^ { \circ } \tan 30 ^ { \circ } } \
&\; \tan 75 ^ { \circ } = \frac { 1 + \frac { 1 } { \sqrt { 3 } } } { 1 - ( 1 ) \left ( \frac { 1 } { \sqrt { 3 } } \right ) } \
&\; \tan 75 ^ { \circ } = \frac { \left ( \frac { \sqrt { 3 } + 1 }{ \sqrt { 3 } } \right ) ( \sqrt { 3 } ) } { \left ( \frac { \sqrt { 3 } - 1 } { \sqrt { 3 } } \right ) ( \sqrt { 3 } ) }\
&\; \tan 75 ^ { \circ } = \frac { \sqrt { 3 } + 1} { \sqrt { 3 } - 1 } \
&\; \tan 75 ^ { \circ } = \left ( \frac { \sqrt { 3 } + 1 } { \sqrt { 3 } - 1 } \right ) \left ( \frac { \sqrt { 3 } + 1 }{ \sqrt { 3 } + 1 } \right ) \
&\; \tan 75 ^ { \circ } = \frac { 3 + 2 \sqrt { 3 } + 1 } { 3 - 1 } \
&\; \tan 75 ^ { \circ } = 2 + \sqrt { 3 }
\end {aligned}
$$

مثال ششم تانژانت

تساوی $$ \tan (180^circ − x) = −tan x $$ را اثبات کنید.

حل: با استفاده از فرمول تانژانت تفاضل دو زاویه، داریم:

$$ \large \begin {aligned}
&\; \tan \left ( 180 ^ { \circ } - x \right ) = \frac { \tan 180 ^ { \circ } - \tan x } { 1 + \tan 180 ^ { \circ } \tan x } \
&\; \tan \left ( 180 ^ { \circ } - x \right ) = \frac { 0 - \tan x } { 1 + ( 0 ) \tan x } \
&\; \tan \left ( 180 ^ { \circ } - x \right ) = - \tan x
\end{aligned}
$$

مثال هفتم تانژانت

تساوی $$ \tan (180^circ + x) = \tan x $$ را اثبات کنید.

حل: با استفاده از فرمول تانژانت مجموع دو زاویه، داریم:

$$ \large \begin {aligned}
&\; \tan \left ( 180 ^ { \circ } + x \right ) = \frac { \tan 180 ^ { \circ } + \tan x } { 1 - \tan 180 ^ { \circ } \tan x } \
&\; \tan \left ( 180 ^ { \circ } + x \right ) = \frac { 0 + \tan x } { 1 - ( 0 ) \tan x } \
&\; \tan \left ( 180 ^ { \circ } + x \right ) = \tan x
\end {aligned}
$$

مثال هشتم تانژانت

تساوی $$ \tan (360^circ − x) = −tan x $$ را اثبات کنید.

حل: با استفاده از فرمول تانژانت تفاضل دو زاویه، داریم:

$$ \large \begin {aligned}
&\; \tan \left ( 360 ^ { \circ } - x \right ) = \frac { \tan 360 ^ { \circ } + \tan x } { 1 + \tan 360 ^ { \circ } \tan x } \
&\; \tan \left ( 360 ^ { \circ } - x \right ) = \frac { 0 - \tan x } { 1 + ( 0 ) \tan x } \
&\; \tan \left ( 360 ^ { \circ } - x \right ) = - \tan x
\end {aligned}
$$

فرمول‌های مثال‌های قبلی در بازنویسی تانژانت‌های زوایایی که بزرگ‌تر از ۹۰ درجه‌اند، بسیار مفید هستند.