ساده کردن کسر ها — به زبان ساده + سوال با جواب

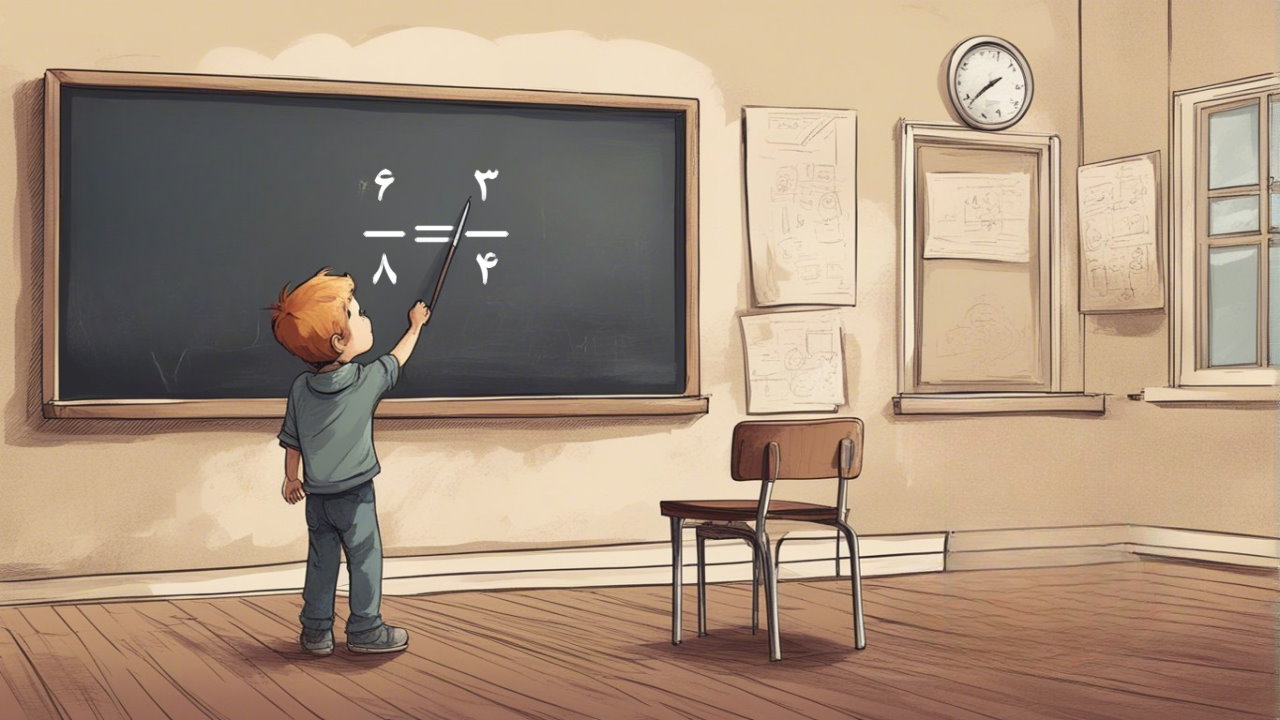
در آموزش‌های پیشین مجله فرادرس، با نسبت در ریاضی آشنا شدیم. دیدیم که یک نسبت را می‌توان به‌شکل یک کسر بیان و آن کسر را در حد امکان ساده کرد. ساده کردن کسر ها به معنای تقسیم صورت و مخرج آن‌ها بر یک عدد است، به‌گونه‌ای که صورت و مخرج هر دو اعدادی صحیح باشند و مقسوم‌علیه یا عامل مشترکی به غیر از عدد ۱ نداشته باشند. نکته مهم در ساده کردن کسر ها این است که اگرچه ما کسرها را ساده می کنیم، اما مقدار کسر بدون تغییر باقی می‌ماند. این بدان معنی است که کسر ساده شده و کسر واقعی یک جفت کسر یا نسبت مساوی را تشکیل می‌دهند. در این آموزش با چند روش آسان برای ساده کردن کسرها آشنا می‌شویم.

ساده کردن کسر چیست؟

ساده کردن یک کسر به معنای تبدیل یک کسر به شکلی است که صورت و مخرج آن عامل مشترکی جز ۱ نداشته باشند. به عبارت دیگر، کسری در صورتی ساده‌ترین شکل خود را دارد که صورت و مخرج آن نسبت به هم اول باشند که معادل با این گفته است که هیچ عامل مشترکی به جز ۱ نداشته باشند.

ساده‌ترین شکل کسر با کسری که آن را ساده کرده‌ایم مساوی یا معادل است. به عنوان مثال، کسر $$\frac 3 5$$ به ساده‌ترین شکل است، زیرا $$3$$ و $$5$$ هیچ عامل مشترکی به جز $$1$$ ندارند. در ادامه، با روش گام به گام ساده کردن کسرها می‌پردازیم.

ساده کردن کسر ها در پایه چهارم دبستان

در این بخش، به روش ساده کردن کسرها در پایه‌ چهارم با ذکر یک مثال می‌پردازیم. ساده کردن کسر یعنی تقسیم صورت بر مخرج. بنابراین، باید ببینیم چگونه می‌توانیم صورت و مخرج را با هم ساده کنیم.

فرض کنید کسر $$\frac {12}{15}$$ را داریم و می‌خواهیم آن را ساده کنیم. ابتدا صورت و مخرج را به‌صورت ضرب اعداد برای حالت‌های مختلف می‌نویسیم. این یعنی:

عدد ۱۲ را می‌توان به دو شکل زیر نوشت:

$$\begin {align} 12 & = 3 \times 4 \\ 12 & = 2 \times 6 \end {align}$$

همچنین، عدد ۱۵ به‌شکل زیر نوشته می‌شود:

$$15 = 3 \times 5$$

اکنون باید ببینیم دو عدد ۱۲ و ۱۵ چه عامل مشترکی دارند که هردو عدد را بر آن تقسیم کنیم. همان‌طور که می‌بینیم، عدد $$3$$ در هر دو عدد مشترک است. بنابراین، می‌توانیم هم صورت و هم مخرج را بر $$3$$ تقسیم کنیم:

$$\frac { 12 } { 15 } = \frac {12 \div 3 } { 15 \div 3 } = \frac { 4 } { 5 }$$

در ادامه، مثال‌های بیشتری را بررسی خواهیم کرد.

اگر می‌خواهید ساده کردن کسرها را به‌خوبی یاد بگیرید، پیشنهاد می‌کنیم روش‌های ساده دیگری را که در ادامه معرفی کرده‌ایم، مطالعه کنید.

ساده کردن کسر ها در پایه پنجم دبستان

در پایه پنجم دبستان، ساده کردن کسرها مربوط به ضرب و تقسیم آن‌هاست که برای یادگیری این مباحث، پیشنهاد می‌کنیم آموزش‌های زیر را مطالعه کنید:

• ضرب کسرها — به زبان ساده + حل تمرین و مثال
• تقسیم کسرها — به زبان ساده + حل تمرین و مثال

برای آشنایی با مباحث ریاضیات دبیرستان، پیشنهاد می‌کنیم به مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه فیلم‌های آموزش‌های دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.

ساده کردن کسرها با کمک عوامل اول

قبل از پرداختن به روش ساده کردن کسرها، بهتر است با مفهوم عامل یا مقسوم‌علیه آشنا شویم.

عامل یا مقسوم علیه چیست؟

مقسومٌ‌ علَیه یا عامل، در ریاضیات به معنای عددی است که عددی دیگر بر آن تقسیم شده است. به عبارت دیگر، عامل‌ها اعدادی هستند که می‌توان آن‌ها را در یکدیگر ضرب کرد و عدد دیگری را به‌ دست آورد. برای مثال، عامل‌های عدد ۶ به‌صورت زیر هستند:

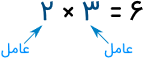
یا عدد ۵۰ را می‌توان این‌گونه نوشت:

$$50 = 2 \times 5 \times 5$$

برای نوشتن عامل‌های یک عدد، کافی است ببینیم آن عدد بر چه اعداد اولی بخش‌پذیر است. برای این کار، ابتدا از کوچک‌ترین عدد اول، یعنی ۲، شورع و عدد را بر آن تقسیم می‌کنیم. برای مثال، فرض کنید می‌خواهیم عدد ۲۴ را برحسب عوامل اول آن بنویسیم. بدین منظور، از ۲ شروع می‌کنیم و می‌بینیم ۲۴ بر ۲ بخش‌پذیر است:

$$24 = 2 \times 12$$

باز هم ادامه می‌دهیم و این بار ۱۲ بر ۲ بخش‌پذیر است (یعنی $$12 = 2 \times 6$$):

$$24 = 2 \times 2 \times 6$$

۶ را نیز می‌توان به‌صورت حاصل‌ضرب دو عدد ۲ و ۳ نوشت ($$6=2 \times 3$$). بنابراین، برای عدد ۲۴، داریم:

$$24 = 2 \times 2 \times 2\times 3$$

دقت کنید که عدد را برحسب مقسوم‌علیه‌های اول نوشتیم، در غیر این صورت می‌توانستیم آن را به‌صورت $$24 = 12 \times 2$$ نیز بنویسیم.

مراحل ساده کردن کسرها با کمک عوامل اول

روش گام به گام ساده کردن کسرها را با یک مثال بیان می‌کنیم. برای مثال، فرض کنید می‌خوهیم کسر $$\frac 8 {12}$$ را ساده کنیم. بنابراین، کسر $$\frac 8 { 12}$$ را در نظر بگیرید و مراحل زیر را دنبال کنید تا یاد بگیرید که چگونه یک کسر را ساده کنید.

مرحله ۱: عوامل (مقسوم‌علیه‌های) صورت و مخرج را بنویسید.

هر عدد، مقسوم علیه‌های مختلفی دارد. ما در اینجا مقسوم‌علیه‌های اول را در نظر می‌گیریم. یعنی مقسوم‌علیه‌هایی که فقط بر خودشان و ۱ بخش‌پذیرند. برای مثال، مقسوم علیه‌های عدد ۱۲، به‌صورت زیر هستند:

$$12 = 2 \times 2 \times 3$$

عدد ۱۲ را به‌صورت زیر نیز می‌توانیم بنویسیم،

$$6 × 2 = 12$$  یا  $$3 × 4 = 12$$  یا  $$12 × 1 = 12$$

اما برای یادگیری بهتر، فقط عوامل اول را در نظر می‌گیریم:

$$12 = 2 \times 2 \times 3$$

صورت کسر عدد ۸ و مخرج عدد ۱۲ است. بنابراین، باید عوامل ۸ و ۱۲ را باید بنویسیم. عوامل اول ۱۲ را تعیین کردیم. کافی است عوامل اول ۸ را تعیین کنیم:

$$8 = 2 \times 2 \times 2$$

بنابراین، عوامل به‌صورت زیر هستند:

• عوامل ۸: ۲ و ۲ و ۲
• عوامل ۱۲: ۲ و ۲ و ۳

مرحله ۲: صورت و مخرج را برحسب عوامل اول بنویسید:

$$\frac 8 { 12 } = \frac { 2 \times 2 \times 2 }{2 \times 2 \times 3 }$$

عوامل مشترک صورت و مخرج را با هم حذف کنید تا زمانی که هیچ عامل مشترکی به جز ۱ وجود نداشته باشد. کسری که به‌دست می‌آید به ساده‌ترین شکل ممکن است.

$$ \require {cancel} \frac 8 { 12 } = \frac { \cancel 2 \times \cancel 2 \times 2 }{ \cancel 2 \times \cancel 2 \times 3 } $$

بنابراین، $$\frac 23$$ ساده‌ترین شکل کسر $$\frac 8 { 12}$$ است.

ساده کردن کسر ها با کمک ب م م

حال، یک راه آسان دیگر را برای ساده کردن کسر ها معرفی می‌کنیم که مشابه این روش، اما سریع‌تر است و می‌توانیم با دنبال کردن فرایند ساده‌سازی کسر، یک کسر پیچیده را تا حد امکان ساده کنیم. شکل زیر را ببینید. در اینجا سه ششم پیتزا را نمایش داده‌ایم.

ساده کردن کسر به معنای ساده کردن آن تا حد امکان است. یک راه سریع برای یافتن ساده‌ترین شکل کسر این است که با بزرگ‌ترین مقسوم‌علیه مشترک کار کنید. برای یادگیری کوتاه‌ترین راه مراحل زیر را دنبال کنید.

مرحله ۱: عوامل یا مقسوم‌علیه‌های اول صورت و مخرج را بنویسید.

مرحله ۲: بزرگ‌ترین مقسوم‌علیه مشترک یا همان ب م م صورت و مخرج را تعیین کنید.

مرحله ۳: صورت و مخرج را بر ب م م تقسیم کنید. کسر به‌دست‌آمده در ساده‌ترین شکل ممکن است.

به‌عنوان مثال، کسر $$\frac 8 {24}$$ را در نظر بگیرید. ب م م دو عدد $$8$$ و $$24$$، عدد $$8$$ است. تقسیم صورت $$8$$ و مخرج $$24$$ بر $$8$$، مستقیماً ساده‌ترین شکل کسر، یعنی $$\frac 13$$ را به ما می‌دهد. بنابراین، کوتاه ترین راه برای نوشتن کسر به ساده‌ترین شکل آن، تقسیم صورت و مخرج بر ب م م آن‌هاست.

ساده کردن کسرهای دارای متغیر

اگر کسری در صورت و مخرج دارای متغیرهای مشترکی باشد، می‌توانیم آن را ساده کنیم. در این حالت، از شکل گسترش‌یافته یا همان بسط هر عبارت در صورت و مخرج استفاده می‌کنیم تا ساده کردن کسر با متغیرها آسان شود.

برای مثال، کسر $$\frac {x^2y} {xy}$$ را در نظر بگیرید.

صورت و مخرج را به‌صورت حاصل ضرب متغیرها بیان کنید.

$$\frac { x^2y} { x y } = \frac { x × x × y} { x × y }$$

متغیرهای مشترک را با هم حذف کنید.

$$\frac { x ^ 2 y } { x y } = \frac { x × x × y} { x × y} = x$$

ساده کردن کسرهای دارای توان

می‌توانیم کسرهای دارای توان در صورت و مخرج را نیز ساده کنیم. بدین منظور، از شکل بسط‌داده‌شده در صورت و مخرج استفاده می‌کنیم تا بتوانیم کسر دارای اعداد توان‌دار را ساده کنیم. برای سهولت خواندن اعداد، گاهی اوقات از نماها استفاده می‌کنیم.

فرض کنید کسر $$\frac { 3 ^ 5 } { 3 ^ 2}$$ را داریم. صورت و مخرج را به‌صورت حاصل‌ضرب اعداد بیان می‌کنیم و سپس اعداد مشترک را با هم حذف می‌کنیم.

$$\frac { 3 ^ 5 } { 3 ^ 2 } = \frac { 3 × 3 × 3 × 3 × 3 } {3 × 3} = 3 × 3 × 3 = 27$$

بنابراین، دیدیم که روش ساده کردن کسرها با اعداد توان‌‌دار بسیار ساده است.

ساده کردن کسرهای مخلوط

کسر مخلوط یا عدد مخلوط عددی است از یک عدد صحیح و یک کسر سره (کسری که قدر مطلق مخرج آن از قدر مطلق صورتش بزرگ‌تر است)‌ تشکیل شده است. برای ساده کردن یک کسر مخلوط، فقط باید قسمت کسری را ساده کنید. برای این کار، کافی است صورت و مخرج را به‌صورت ضرب عوامل بنویسید و سپس عوامل مشترک را حذف کنید. حاصل عدد جدید و مخرج جدید کسر مخلوط خواهد بود.

به عنوان مثال، کسر مخلوط زیر را ساده می‌کنیم:

$$3 \frac 4 { 10 }$$

برای ساده کردن کسر مخلوط $$3 \frac 4 { 10 }$$، کافی است فقط قسمت کسری را ساده کنیم. صورت و مخرج بخش کسری را به‌صورت ضرب عوامل می‌نویسیم و عوامل مشترک صورت و مخرج را حذف می‌کنیم.

$$\frac { 4 } {10} = \frac { 2 × 2 } { 2 × 5 } = \frac 2 5$$

بنابراین، کسر مخلوط $$3 \frac 4 { 10 }$$ را می‌توان به‌شکل ساده شده $$3 \frac 25$$ نوشت.

ساده کردن کسرهای ناسره

کسرهای ناسره کسرهایی هستند که صورت آن‌ها بزرگ‌تر یا مساوی مخرجشان باشد. برای ساده کردن کسرهای ناسره، مانند کسرهای عادی عمل می‌کنیم. مثلاً کسر $$\frac {15 } { 12}$$ را این‌گونه ساده می‌کنیم:

$$\frac {15 } { 12} = \frac {15 \div 3 } { 12 \div 3 } = \frac 54 = 1\frac 14$$

یک راه دیگر این است که اغین کسرها را ابتدا به کسرهای مخلوط تبدیل کنیم. برای این کار، باید صورت را بر مخرج تقسیم کنیم. سپس با قرار دادن ضریب به عنوان عدد کامل، باقیمانده به عنوان صورت و مقسوم‌علیه به عنوان مخرج، آن را به‌صورت اعداد مخلوط بنویسیم. مثال زیر را برای درک بهتر این موضوع مرور کنیم.

به عنوان مثال، برای ساده کردن کسر ناسره $$\frac {11} 4$$، باید $$11$$ را بر $$4$$ تقسیم کنیم و پس از انجام تقسیم، مقادیر ضریب و باقیمانده را به‌دست آوریم. وقتی $$\frac { 11 } 4$$ را تقسیم می‌کنیم، $$2$$ به‌عنوان ضریب و $$3$$ به‌عنوان باقیمانده به‌دست می‌آید. بنابراین، شکل ساده شده کسر ناسره $$\frac { 11 } 4$$، به‌صورت $$2 \frac 34$$ است.

مثال‌های ساده کردن کسر ها

در این بخش، مثال‌هایی را از ساده کردن کسرها بررسی می‌کنیم.

مثال اول ساده کردن کسر ها

کسر $$\frac  2 7$$ را ساده کنید.

حل: این کسر تا جایی که امکان داشته ساده شده و ساده‌تر از این نمی‌شود.

مثال دوم ساده کردن کسر ها

کسر $$\frac {16}{30}$$ را ساده کنید.

حل: ابتدا اعداد صورت و مخرج را به‌شکل ضرب عواملشان می‌نویسیم.

عدد $$16$$ را می‌توان به دو شکل زیر نوشت:

$$\begin {align} 16 & = 4 \times 4 \\ 16 & = 2 \times 8 \end {align}$$

عدد $$30$$ را نیز می‌توان این‌گونه نوشت:

$$\begin {align} 30 & = 5 \times 6 \\ 30 & = 2 \times 15 \end {align}$$

همان‌طور که مشخص است، دو عدد عامل مشترک $$2$$ را دارند. بنابراین، می‌توانیم صورت و مخرج را بر $$2$$ تقسیم کنیم و بنویسیم:

$$\frac { 16 } { 30 } = \frac {16 \div 2 } { 30 \div 2 } = \frac { 8 } { 15 }$$

مثال سوم ساده کردن کسر ها

کسر $$\frac 4 {20 }$$ را ساده کنید.

حل: عدد $$20$$ را می‌توانیم به شکل $$20=4\times 5$$ بنویسیم. صورت کسر نیز $$4 = 4 \times 1$$ است. بنابراین، به راحتی می‌توانیم صورت و مخرج را بر عدد $$4$$ تقسیم کنیم:

$$\frac 4 {20 } = \frac { 4 \div 4 } { 20 \div 4} = \frac 1 {5 }$$

می‌توانیم این‌گونه نیز بنویسیم:

$$ \require {cancel} \frac 4 {20 } = \frac { \cancel 4 \times 1 } { \cancel 4 \times 5 } = \frac 1 {5 } $$

مثال چهارم ساده کردن کسر ها

کسر $$\frac 4 { 100}$$ را ساده کنید.

حل: این بار از ب‌ م م استفاده می‌کنیم. ابتدا عوامل یا همان مقسوم‌علیه‌های دو عدد صورت و مخرج را می‌نویسیم:

• مقسوم‌علیه‌های عدد ۴: ۲ و ۴
• مقسوم‌علیه‌های عدد ۱۰۰: ۲ و ۴ و ۵ و ۱۰ و ۲۰ و ۵۰ و ۱۰۰

می‌بینیم که بزرگ‌ترین مقسوم‌علیه مشترک این دو عدد ۴ است. بنابراین، صورت و مخرج را بر ۴ تقسیم می‌کنیم:

$$ \require {cancel} \frac 4 {100 } = \frac { 4 \div 4 } { 100 \div 4 } = \frac 1 { 25} $$

مثال پنجم ساده کردن کسر ها

کسر $$\frac {36}{51}$$ را ساده کنید.

حل: با نگاهی به صورت و مخرج کسر، می‌بینیم که هر دو عدد بر ۳ بخش‌پذیر هستند، زیرا مجموع ارقام آن‌ها بر ۳ بخش‌پذیر است. بنابراین، می‌توانیم صورت و مخرج را بر ۳ تقسیم کنیم تا کسر ساده شود:

$$ \require {cancel} \frac {36}{51} = \frac {\cancel 3 \times 12} {\cancel 3 \times 17} = \frac {12} { 17 } $$

آزمون سنجش یادگیری ساده کردن کسر

در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث ساده کردن کسر را با طرح سوال‌های چندگزینه‌ای می‌سنجیم. پس از جواب دادن به تمام سوال‌ها، نتیجه آزمون برای شما به نمایش درمی‌آید.