فرادرس
فرمول دنباله هندسی — به زبان ساده و با مثال
دنباله و سری‌ها، یکی از مهم‌ترین ابزارهای ریاضیات هستند. در این بین تصاعد یا دنباله حسابی و دنباله هندسی شاید از همه بیشتر به کار می‌روند. در این نوشتار از مجله فرادرس، به به دنبال پیدا کردن فرمول دنباله هندسی هستیم و براساس آن رابطه محاسبه سری هندسی را هم معرفی خواهیم کرد. استفاده از مثال‌های متعدد و همچنین نمایش تصاعدها به وسیله نمودار، به درک بهتر این مفاهیم کمک خواهد کرد.
در متن‌های مربوط به دنباله هندسی خواندید که قدر نسبت و جمله اول در تصاعد یا دنباله هندسی نقش مهمی دارند. همچنین شرط همگرایی و واگرایی سری دنباله هندسی نیز در مطالب دیگر مجله فرادرس، بحث شده است. در این متن بیشتر می‌خواهیم مبانی نظری و فرمول دنباله هندسی را استخراج کرده و خصوصیات آن را مورد بررسی قرار دهیم. شرط همگرایی برای جمع جملات دنباله هندسی نیز در اینجا مورد اشاره قرار گرفته و به آن خواهیم پرداخت.
فرمول دنباله هندسی
در ریاضیات، یک تصاعد یا دنباله هندسی، دنباله ای از اعداد غیر صفر است که هر جمله آن با جمله قبلی در یک ثابت تفاوت دارد. به این ترتیب اگر مقدار ثابتی را در جمله اول ضرب کنیم، جمله دوم حاصل می‌شود. به همین ترتیب، جمله سوم از ضرب جمله دوم در مقدار ثابت محاسبه خواهد شد. جمله چهارم هم مضربی از جمله سوم است. به همین ترتیب، جمله‌های بعدی تصاعد یا دنباله هندسی پدید می‌آیند.
از طرفی قدر نسبت یا مقدار نسبت مشترک، مقدار ثابتی است که در هر جمله ضرب شده تا جمله بعدی را بوجود آورد. در اغلب متن‌های ریاضی، قدر نسبت را با $$r$$ نشان می‌دهند. مقدار $$r$$ در تصاعد هندسی، در بیشتر موارد، عددی صحیح (مثبت یا منفی) است. ولی انتخاب عدد گویا برای مقدار قدر نسبت، نیز در تصاعد هندسی مرسوم است. حتی گاهی این عدد را از بین اعداد مختلط انتخاب می‌کنند.
به عنوان مثال، توالی 2 ، 6 ، 18 ، 54 ، … یک تصاعد یا دنباله هندسی با قدر نسبت 3 است. به همین ترتیب 10 ، 5 ، 2٫5 ، 1٫25 ، … یک توالی هندسی با قدر نسبت یا مقدار نسبت مشترک ۰٫۵ است. شکل کلی و عمومی یک توالی یا تصاعد هندسی به صورت نوشته می‌شود.
$$ \large {\displaystyle a, \ ar, \ ar ^ {2}, \ ar ^ {3}, \ ar ^ {4}, \ \ldots} $$
در رابطه بالا r ≠ 0 «نسبت مشترک» (Common Ratio) یا قدر نسبت است و a ≠ 0 «عامل مقیاس» (Scale Factor) بوده که همان «مقدار شروع دنباله» (Initial Value) یا نقطه اولیه را نشان می‌دهد.
نکته: تمایز بین یک تصاعد یا دنباله و یک سری این است که یک تصاعد، توالی از مقادیر است که ممکن است متناهی یا نامتناهی باشند. در حالی که یک سری یک مقدار است که از جمع مقادیر تصاعد یا دنباله حاصل می‌شود. در صورتی که یک تصاعد نامتناهی وجود داشته باشد، باید شرایطی را برای همگرایی سری حاصل از آن، مورد بررسی قرار دهیم تا مجموع جملات دنباله، مشخص شود.
ساختن فرمول دنباله هندسی
همانطور که گفتیم، هر جمله در فرمول دنباله هندسی به صورت ضرب مقدار ثابت (جمله اول) در توان‌های متوالی از قدر نسبت ساخته می‌شود. به رابطه زیر توجه کنید.
$$ \large {\displaystyle x_{ n} = a \, r ^ { n – 1}} $$
رابطه ۱: فرمول دنباله هندسی
البته در اینجا هم فرض‌های $$r \neq 0 , a \neq 0 $$ را داریم. توجه داشته باشید که رابطه ۱، تعریفی برای دنباله هندسی محسوب می‌شود ولی در ادامه رابطه بازگشتی به کمک این تعریف، در رابطه ۲، ساخته می‌شود که البته هر دو، نتیجه یکسانی برای تولید جمله‌های دنباله هندسی دارند.
مثال: با انتخاب $$a=5$$ و $$ r = 3$$، فرمول دنباله هندسی را به کار برده و یک تصاعد هندسی می‌سازیم. واضح است که باید از رابطه زیر کمک گرفته و مقادیر $$r$$ و $$a$$ را جایگزین کنیم.
$$ \large {\displaystyle x_{n} = a \, r ^ { n – 1}} $$
در نتیجه
$$ \large {\displaystyle x_{ n} = 5 \times \, 3 ^ { n – 1}} $$
پس جمله‌های مربوط به فرمول دنباله هندسی به صورت زیر درخواهد آمد.
$$ \large {\displaystyle x_1 = 5 \times 3^0 = 5, \; x_2 = 5 \times 3^1 = 15, \; x_3 = 5 \times 3^2 = 45, \; x_4 = 5 \times 3^3 = 135 , \; \ldots } $$
نکته: اگر $$r= 1$$ باشد، دنباله ساخته شده باز هم هندسی است، ولی جملات آن، همگی با هم برابرند. از طرفی با انتخاب $$r = -1$$ نیز مقادیر دنباله هندسی، یکی در میان مثبت و منفی خواهند بود که مقادیر مثبت با یکدیگر و مقادیر منفی نیز با هم یکسان بدست می‌آیند. با انتخاب صفر برای قدر نسبت، همه جملات صفر شده و در نتیجه دنباله‌ای ایجاد نخواهد شد. به همین دلیل در تعریف دنباله هندسی، شرط $$r \neq 0 $$ را قید کرده بودیم.
مثال: دنباله هندسی را با انتخاب $$a=5$$ و $$ r = -3$$، ایجاد کرده و به کمک فرمول دنباله هندسی مقادیر آن را می‌نویسیم. برای اینکه جمله‌های این مثال با مثال قبل اشتباه نشود، آن‌ها را با $$y$$ نشان می‌دهیم.
$$ \large {\displaystyle y_1 = 5 \times (-3 )^0 = 5, \; y_2 = 5 \times (-3 )^1 = -15, \; y_3 = 5 \times (-3 )^2 = 45, \; y_4 = 5 \times (-3 )^3 = -135 , \; \ldots } $$
در تصویر زیر مقادیر تصاعد یا دنباله هندسی هر دو مثال ($$x_n$$ و $$y_n$$) ترسیم و مقایسه شده‌اند.
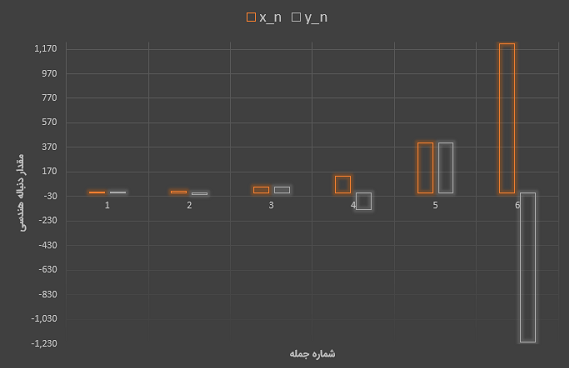
مثال: این مثال به موردی اشاره می‌کند که قدر نسبت در فرمول دنباله هندسی مقداری مثبت بوده ولی از ۱ کوچکتر است. چنین دنباله‌ای نزولی نامیده می‌شود، زیرا با افزایش اندیس یا تعداد جملهها، مقدارشان کاهش می‌یابد.
قدر نسبت را $$r= \tfrac{1}{2}$$ در نظر بگیرید. از طرفی، جمله اول هم به اختیار خودمان، برابر با ۱۰۰ است. طبق رابطه ۱، جملات بعدی این تصاعد را محاسبه و در جدول زیر نمایش می‌دهیم.
$$ \large {\displaystyle x_{n} = a \, r ^ { n – 1} \xrightarrow { x_1 = a = 100, r = \tfrac{1}{2} } x_n = 100 \times (\tfrac{ 1}{ 2})^{( n – 1) }} $$
| اندیس یا شماره جمله (n) | x_n |
| 1 | $$ \large {\displaystyle x_1= 100 }$$ |
| 2 | $$ \large {\displaystyle x_2 = \tfrac{1}{2} \times x_1 = \tfrac{1}{2} \times 100 = 50 }$$ |
| 3 | $$ \large {\displaystyle x_3 = \tfrac{1}{2} \times x_2 = \tfrac{1}{2} \times 50 = 25 }$$ |
| 4 | $$ \large {\displaystyle x_4 = \tfrac{1}{2} \times x_3 = \tfrac{1}{2} \times 25 = 12.5 }$$ |
| 5 | $$ \large {\displaystyle x_5 = \tfrac{1}{2} \times x_4 = \tfrac{1}{2} \times 12.5 = 6.25 }$$ |
| … | … |
رابطه بازگشتی برای فرمول دنباله هندسی
شیوه دیگر برای پیدا کردن فرمول دنباله هندسی و نوشتن جملات آن، استفاده از ارتباط بین جمله‌های متوالی است. می‌دانیم که جمله $$n$$ام یک دنباله صعودی به صورت زیر نوشته می‌شود.
$$ \large {\displaystyle x_{ n} = a \, r ^ { n – 1}} $$
بنابراین جمله قبلی یعنی جمله $$n-1$$ام نیز به شکل زیر خواهد بود.
$$ \large {\displaystyle x_{ n -1} = a \, r ^ {n – 2}} $$
این بار این دو جمله را از بر هم تقسیم می‌کنیم تا به یک معادله بازگشتی برسیم.
$$ \large {\displaystyle x_{ n} \div x_{ n -1 }= \dfrac{ a \, r ^ {n-1}}{ a \, r ^ {n – 2}} } $$
از سمت راست تساوی بالا، از ساده‌سازی کسر را انجام داده و به نتیجه زیر خواهیم رسید.
$$ \large {\displaystyle x_{ n} \div x_{ n -1 }= r^{ n -1 – ( n – 2) } = r } $$
با استفاده از طرفین وسطین یا ضرب متقاطع، نتیجه رابطه بازگشتی یا تفاضلی برای فرمول دنباله هندسی به صورت زیر حاصل می‌شود.
$$ \large {\displaystyle x_{ n} \div x_{ n -1 }= r^{ n -1 – ( n – 2) } = r \rightarrow x_n = r \cdot x_{ n – 1} } $$
رابطه ۲: رابطه بازگشتی برای فرمول دنباله هندسی
اغلب رابطه سمت راست را به عنوان «جمله عمومی دنباله هندسی» به کار می‌برند.
مثال: باز هم همان دنباله‌های هندسی قبلی را ایجاد می‌کنیم ولی این بار از رابطه بازگشتی فرمول دنباله هندسی کمک می‌گیریم. در نظر بگیرید که جمله اول $$a=5$$ و قدر نسبت $$ r = 3$$، است. فرمول را به صورت زیر به کار می‌بریم.
$$ \large {\displaystyle x_n = r \cdot x_{ n – 1} \xrightarrow{ r = 3, x_1 = 5} x_n = 3 x_{n-1} }$$
جدول زیر به ازاء مقادیر مختلف $$n$$، جملات این تصاعد هندسی را مشخص کرده است.
| اندیس یا شماره جمله (n) | x_n |
| 1 | $$ \large {\displaystyle x_1= 5 }$$ |
| 2 | $$ \large {\displaystyle x_2 = 3 \times x_1 = 3 \times 5 = 15 }$$ |
| 3 | $$ \large {\displaystyle x_3 = 3 \times x_2 = 3 \times 15 = 45 }$$ |
| 4 | $$ \large {\displaystyle x_4 = 3 \times x_3 = 3 \times 45 = 135 }$$ |
| 5 | $$ \large {\displaystyle x_5 = 3 \times x_4 = 3 \times 135 = 405 }$$ |
| … | … |
همانطور که می‌بینید، با استفاده از رابطه بازگشتی همان مقادیر دنباله تصاعد هندسی ساخته شد. در مثال بعدی، رابطه بازگشتی را برای قدر نسبت کسری به کار می‌بریم.
مثال: جمله عمومی دنباله‌ای به صورت زیر است. می‌خواهیم جمله‌های آن را استخراج کنیم. البته احتیاج است که جمله اول را هم مشخص کنیم. در اینجا فرض بر این است که $$x_1 = a = 100$$ است.
$$ \large {\displaystyle x_n = (\tfrac{1}{5}) \cdot x_{ n – 1} } $$
طبق جدول زیر و رابطه بالا، جملهها را یک به یک و برحسب $$n$$ محاسبه و مشخص می‌کنیم.
| اندیس یا شماره جمله (n) | x_n |
| 1 | $$ \large {\displaystyle x_1= 100 }$$ |
| 2 | $$ \large {\displaystyle x_2 = \dfrac{1}{5} \times x_1 = \dfrac{1}{5} \times 100 = 20 }$$ |
| 3 | $$ \large {\displaystyle x_3 = \dfrac{1}{5} \times x_2 = \dfrac{1}{5} \times 20 = 4 }$$ |
| 4 | $$ \large {\displaystyle x_4 = \dfrac{1}{5} \times x_3 = \dfrac{1}{5} \times 4 = \dfrac{4}{5} }$$ |
| 5 | $$ \large {\displaystyle x_5 = \dfrac{1}{5} \times x_4 = \dfrac{1}{5} \times \dfrac{4}{5} = \dfrac{4}{25} }$$ |
| … | … |
مثال: باز هم از همان جمله عمومی قبلی برای این مثال استفاده می‌کنیم ولی این بار قدر نسبت را بزرگتر از $$\dfrac{1}{5} $$در نظر می‌گیریم و آن را $$ r = \dfrac{1}{2}$$ قرار می‌دهیم. جمله اول هم همان ۱۰۰ است.
$$ \large {\displaystyle y_n = (\tfrac{1}{2}) \cdot y_{ n – 1} } $$
به جدول زیر که براساس فرمول دنباله هندسی بالا ساخته شده، دقت کنید.
| اندیس یا شماره جمله (n) | x_n |
| 1 | $$ \large {\displaystyle y_1= 100 }$$ |
| 2 | $$ \large {\displaystyle y_2 = \dfrac{1}{2} \times y_1 = \dfrac{1}{2} \times 100 = 50 }$$ |
| 3 | $$ \large {\displaystyle y_3 = \dfrac{1}{2} \times y_2 = \dfrac{1}{2} \times 50 = 25 }$$ |
| 4 | $$ \large {\displaystyle y_4 = \dfrac{1}{2} \times y_3 = \dfrac{1}{2} \times 25 = \dfrac{25}{2} }$$ |
| 5 | $$ \large {\displaystyle y_5 = \dfrac{1}{2} \times y_4 = \dfrac{1}{2} \times \dfrac{25}{2} = \dfrac{25}{4} }$$ |
| … | … |
همانطور که تشخیص می‌دهید، زمانی که قدر نسبت بین ۰ و ۱ باشد، دنباله نزولی است. از طرفی نزدیک بودن قدر نسبت در این حالت به ۱ باعث می‌شود که دنباله به آرامی شیب نزولی داشته باشد. در حالیکه نزدیک بودن قدر نسبت به صفر، شیب نزولی را افزایش می‌دهد. برای روشن‌تر شدن موضوع نمودار زیر را برای دو مثال قبلی ترسیم کرده‌ایم.
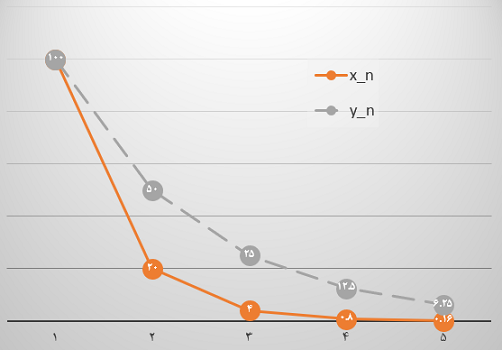
نکته: همانطور که گفتیم، اگر قدر نسبت بزرگتر از ۱ باشد، دنباله هندسی، صعودی است. از طرفی بزرگ بودن مقدار قدر نسبت در این حالت، باعث افزایش شیب صعود در این دنباله‌ها خواهد بود.
در بسیاری از رشته‌ها، مانند مدیریت و اقتصاد، سری و دنباله‌ها مطرح و به کار گرفته می‌شوند. در آموزش ریاضی و آمار (۱) که برای پایه دهم علوم انسانی توسط فرادرس منتشر شده است، بخشی به قوانین مربوط به دنباله و سری اختصاص دارد. لینک دسترسی به این آموزش در ادامه آورده شده است.
- برای مشاهده فیلم آموزش ریاضی و آمار (۱) – پایه دهم علوم انسانی + اینجا کلیک کنید.
تشخیص یک دنباله هندسی
فرض کنید یک دنباله به صورت زیر در اختیار شما قرار گرفته است، می‌خواهیم تشخیص بدهیم که آیا این الگو اعداد، مطابق با فرمول دنباله هندسی است یا خیر؟
$$ \large {\displaystyle x_1, \ x_2, \ x_3, \ x_4, \ x_5, \ \ldots} $$
برای این کار، باید جملات متوالی این دنباله را دو به دو، بر هم تقسیم کنیم. اگر خارج قسمت مربوط به این تقسیم‌ها، برابر باشد، می‌توان، تصاعد را هندسی بنامیم. این شرط را به صورت زیر نمایش می‌دهیم.
$$ \large {\displaystyle \dfrac{ x_2}{ x_1} = \dfrac{ x_3}{ x_2} =\dfrac{ x_4}{ x_3} = \ldots = r} $$
یا به طور کلی شرط به شکل زیر تعیین می‌شود.
$$ \large {\displaystyle r = \dfrac{ x_{i + 1}}{ x_{ i }} , \;\;\; i \geq 1} $$
مثال: بررسی کنید که الگوی اعداد زیر، مطابق با فرمول دنباله هندسی است یا خیر؟
$$ \large {\displaystyle 20,\ 10,\ 5,\ 2.5,\ 1.25, \ldots} $$
همانطور که گفتیم، باید تقسیمات جملات متوالی را دو به دو اجرا کنیم.
$$ \large {\displaystyle \dfrac{ 10}{ 20} = \dfrac{ 5}{ 10} = \dfrac{ 2.5}{ 5} = \ldots = \dfrac{ 1}{ 2} = r} $$
مشخص است که خارج قسمت‌ها، یکسان و برابر هستند. در نتیجه دنباله مورد نظر، یک دنباله هندسی است که البته به علت آن که $$ r = \frac{1}{2}$$ بوده، یک دنباله نزولی نیز خواهد بود.
با توجه به شرایطی که برای دنباله‌های هندسی پیدا می‌کنیم، می‌توانیم آن‌ها را همگرا یا واگرا در نظر بگیریم. منظور از همگرایی آن است که اگر یک دنباله، تا بی‌نهایت ادامه یابد، مقادیر انتهایی این دنباله، به یک مقدار ثابت می‌رسند و تغییرات از یک نقطه به بعد در دنباله، محسوس نیست.
دنباله‌های صعودی اغلب چنین نیستند ولی دنباله‌های نزولی یا دنباله‌های متناوب می‌توانند به صورت یک دنباله همگرا ظاهر شوند. در تصویر زیر یک نمونه از دنباله همگرا را مشاهده می‌کنید که به صورت متناوب بوده و با افزایش $$n$$ (روی محور افقی) به مقدار ثابتی (روی محور عمودی) نزدیک می‌شود. چنین دنباله‌ای به «دنباله کوشی» (Cauchy Sequence) معروف است.
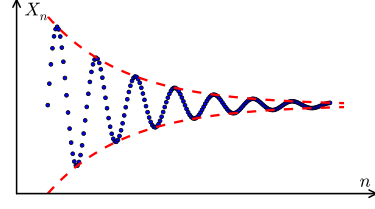
واسطه هندسی و رابطه بین جمله‌های متوالی
سه جمله از یک تصاعد هندسی را به ترتیب در نظر بگیرید که آن‌ها را به شکل $$x$$ و اندیس مکانی یعنی $$n$$ نام‌گذاری کرده‌ایم. پس اگر $$x_n, x_{(n+1)} , x_{(n+2)}$$ این سه جمله را مشخص کرده باشند، ناتساوی‌های $$x_n \leq x_{(n+1)} \leq x_{(n+2)}$$ برایشان وجود دارد. طبق فرمول دنباله هندسی برای هر یک از آن‌ها رابطه‌های زیر را داریم. البته از آنجایی که نمی‌دانیم این سه عبارت، چندمین عبارت از تصاعد هندسی هستند، هر یک از آن‌ها را برحسب $$n$$ مشخص کرده‌ایم. از طرفی $$r$$ را قدر نسبت و $$a$$ را جمله اول یا عامل مقیاس می‌شناسیم.
$$ \large {\displaystyle x_n = a\ r^{( n – 1)} }$$
$$ \large {\displaystyle x_{( n + 1)} = a\ r^{( n)} }$$
$$ \large {\displaystyle x_{( n + 2)} = a\ r^{( n + 1)} }$$
حال جمله وسط را برحسب جمله قبلی و جمله بعدی می‌نویسیم.
$$ \large {\displaystyle x_{( n + 1)} = \overbrace{a\ r^{( n -1 )}}^{ x_n}\;\; r = x_{(n)} r}$$
$$ \large {\displaystyle x_{( n + 1)} = \overbrace{a\ r^{(n + 1)}}^{ x_{( n + 2)}}\; / \; r =\dfrac{ x_{(n + 2)}}{ r}}$$
حال طرف راست تساوی ها را در هم و طرف چپ تساوی‌ها را هم در یکدیگر ضرب می‌کنیم. واضح است که علامت تساوی در جمله جدید برقرار است زیرا دو چیز مساوی را در یکدیگر ضرب کرده‌ایم.
$$ \large {\displaystyle x_{( n + 1)} \times x_{( n + 1)} = x_{( n + 1)}^2 } $$
و
$$ \large {\displaystyle (x_{(n)} \times\ \color{red}{ \not{ \color{black}{r}}} )\times (\dfrac{x_{(n + 2)}} { \color{ red}{ \not{ \color{black}{r}}}}) = x_{ n} \times\ x_{( n + 2 )}}$$
در نتیجه تساوی زیر برقرار خواهد بود.
$$ \large {\displaystyle x_{( n + 1)}^2 = x_{ n} \times \ x_{ ( n + 2 )}} $$
رابطه ۳: واسطه هندسی برای جملات دنباله هندسی
رابطه بالا به واسطه هندسی نیز معروف است. می‌توان این رابطه را به میانگین هندسی نیز تعمیم داد. به این معنی که اگر جمله وسط را میانگین جمله قبلی و بعدی در نظر بگیریم، مقدار آن از طریق ریشه دوم حاصل ضرب جمله قبل و بعد بدست می‌آید.
مثال: فرض کنید سه جمله متوالی از یک تصاعد هندسی به صورت $$3 , 9 , 27$$ است. رابطه واسطه هندسی را برای این دنباله تحقیق می‌کنیم.
$$ \large {\displaystyle 9^2 = 81 = 27 \times 3 }$$
مجموع جملات دنباله هندسی
یک دنباله هندسی را در نظر بگیرید. اگر مجموع این جملات را تا اندیس $$n$$ام بدست آوریم، یک دنباله دیگر ساخته شده که به آن «سری هندسی» (Geometric Series) گفته می‌شود. پس رابطه بین دنباله هندسی و سری هندسی آن است که سری براساس جمع جملات دنباله هندسی پدید می‌آید.
فرض کنید که دنباله هندسی به صورت جمله‌های زیر دارید.
2, 10, 50, 250
واضح است که با کمی سعی و کوشش می‌توان فهمید که مقدار $$a$$ در این دنباله، عدد ۲ و قدر نسبت هم ۵ است. حال مجموع این جملهها را بدست می‌آوریم.
$$ \large {\displaystyle {\displaystyle 2 + 1 0 + 5 0 + 2 5 0 = 2 + 2 \times 5 + 2 \times 5^{ 2 } + 2 \times 5^{ 3 }} }$$
جالب است که این مجموع از طریق رابطه زیر به راحتی قابل محاسبه است.
$$ \large \sum_{ n = 1 }^{ N} a r^{ n – 1 }={ \dfrac {a ( 1 – r^{N})}{ 1 – r }}$$
رابطه 4: مجموع جملات یک تصاعد هندسی (سری هندسی)
در رابطه بالا، $$N$$ تعداد جملات، $$r$$ قدر نسبت و $$a$$ نیز جمله اول یا ابتدایی تصاعد هندسی است. پس، برای تصاعد هندسی گفته شده، مجموع به شکل زیر حاصل می‌شود.
$$ \large {\displaystyle 2 + 1 0 + 5 0 + 2 5 0 = { \dfrac { 2( 1 – 5^{ 4})}{ 1 – 5 } }={ \dfrac { -1248}{ -4}}= 312}$$
رابطه بالا برای تمامی اعداد حقیقی $$a$$ و $$r \neq 1$$ صادق است. برای مثال، در ادامه یک فرمول دنباله هندسی با قدر نسبت $$-2\pi$$ و $$a = 1$$ را مشاهده می‌کنید که مجموع آن بدست آمده. واضح است که دنباله حاصل، متناوب بوده و مقدار تقریبی حاصل جمع آن برای سه جمله اول بدست آمده است.
$$ \large {\displaystyle -2 \pi +4 \pi ^{2} – 8 \pi ^{3} = -2 \pi +( -2 \pi )^{2} +( -2 \pi )^{ 3} = \\ \large{ \dfrac { -2 \pi (1- (-2 \pi )^{3 } )}{ 1- (-2 \pi )} }={ \dfrac {-2 \pi (1 + 2 \pi ^{ 3})}{ 1 + 2 \pi }} \approx -54.360768}$$
معرفی فیلم آموزش ریاضی و آمار (۱) – پایه دهم علوم انسانی
تفهیم و کمک به درک موارد و موضوعات درس ریاضی و آمار سال دهم رشته‌های ادبیات و علوم انسانی و علوم و معارف اسلامی، هدف اصلی این آموزش است. دانش آموزانی که تمایل به یادگیری بهتر و بیشتر ریاضی دارند، می‌توانند با مشاهده این فیلم آموزشی، به صورت اصولی و با مثال‌های فراوان، با مسائل و موضوعات ریاضی در این پایه، آشنا شوند.
در این آموزش سعی بر این است که با بیان روان و منسجم، سرفصل‌های کتاب درسی بیان شده، به طوری که دانش‌آموز احساس کند در کلاس درس حضور دارند و احتیاجی به مرور منابع دیگر آموزشی نداشته باشند. شایان ذکر است که در این فرادرس، تمامی مباحث کتاب درسی را پوشش می‌دهد و می‌توانید با صرف وقتی بسیار کمتر از زمان کلاس درس، از آن بهره برده و مباحث ریاضی و آمار را بیاموزید.
این فیلم آموزشی شامل چهار درس است. درس یکم به روش حل معادله درجه دوم می‌پردازد. البته در این بین اتحادهای ریاضی و روش تجزیه نیز مطرح می‌شود. درس دوم توابع ریاضی و شیوه ترسیم آن‌ها را توضیح داده و در درس سوم، آمار و مباحث مرتبط با شاخص‌های مرکزی و پراکندگی مطرح می‌شود. درس چهارم نیز نمودارهای آماری یک و چند متغیره را مطرح کرده و طیف وسیعی از گراف‌ها را معرفی می‌کند.
این آموزش برای کلیه دانش آموزان علوم انسانی و علوم و معارف اسلامی – دوره دوم متوسطه مناسب بوده و تماشای فیلم آموزشی آن ۶ ساعت و ۱۹ دقیقه زمان احتیاج دارد.
- برای مشاهده فیلم آموزش ریاضی و آمار (۱) – پایه دهم علوم انسانی + اینجا کلیک کنید.
خلاصه و جمع‌بندی
در این متن به فرمول دنباله هندسی پرداختیم و براساس مقدار اولیه و قدر نسبت شکل یا فرمول عمومی دنباله هندسی را مشخص کردیم. از طرفی برای یک دنباله هندسی، مجموع را هم مشخص کردیم که به آن یک سری هندسی می‌گویند. شرایط مربوط به همگرایی این مجموع را برای زمانی که بی‌نهایت عبارت از دنباله هندسی در اختیارمان باشد، مشخص کردیم. مثال‌هایی که در این متن به آن‌ها پرداختیم به منظور روشن‌تر شدن موضوع کمک شایان می‌کند. پیشنهاد می‌کنیم که با مطالعه دقیق این مثال‌ها، درک مناسبی از سری و دنباله هندسی کسب کنید.
