فرادرستبدیل واحد زاویه — به زبان ساده
در طول تاریخ، زاویه با واحدهای مختلفی اندازه‌گیری شده است. معروف‌ترین واحدها یا یکاهای اندازه‌گیری زاویه درجه ($$^\circ$$) و رادیان (rad) هستند، اما واحدهای دیگری نیز وجود دارند که می‌توان زاویه را برحسب آن‌ها بیان کرد. در این آموزش، واحدهای اندازه‌گیری زاویه و تبدیل واحد زاویه را بیان خواهیم کرد.
واحدهای اندازه‌گیری زاویه
همان‌طور که گفتیم، زاویه واحدهای مختلفی دارد که برخی از آن‌ها مثل درجه و رادیان معروف‌تر هستند.
جدول زیر واحدهای اندازه‌گیری زاویه را نشان می‌دهد. از آنجا که درجه واحد ملموس‌تری است، هر کدام از این واحدها برحسب درجه بیان شده‌اند.
| نام | چرخش (درجه) |
| دور | $$ 360 ^ \circ $$ |
| ضریب $$ \pi$$ | $$ 180 ^ \circ $$ |
| ربع | $$ 90 ^ \circ $$ |
| یک‌ششم دایره یا سکستانت | $$ 60 ^ \circ $$ |
| رادیان | $$ 57^ \circ 17 ^ \prime $$ |
| درجه باینری | $$ 1 ^ \circ 33 ^ \prime 45 ^ {\prime \prime } $$ |
| درجه | $$ 1 ^ \circ $$ |
| گرادیان | $$ 0 ^ \circ 54 ^ \prime $$ |
| دقیقه قوسی | $$ 0 ^ \circ 1 ^ \prime $$ |
| ثانیه قوسی | $$ 0 ^ \circ 0 ^ \prime 1 ^ {\prime \prime } $$ |
در جدول بالا، دقیقه قوسی نیز با نماد $$^\prime$$ مشخص شده و برابر با $$ 1 ^\prime = 1/60^ \circ $$ است. یک ثانیه قوسی نیز با نماد $$ ^{\prime \prime}$$ مشخص شده و برابر با $$ 1 ^ {\prime \prime} = 1/ 3600^ \circ $$ است.
در ادامه، واحدهای رایج رادیان، گرادیان و درجه را با جزئیات بیشتری معرفی می‌کنیم.
رادیان
یک رادیان (Radian)، اندازه زاویه‌ای است که قوسی از دایره را می‌گستراند که طول آن قوس برابر با شعاع دایره است. رادیان واحد اندازه‌گیری زاویه در دستگاه بین‌المللی یکاها (SI) است. طبق تعریف، رادیان بدون بعد بوده و برای جلوگیری از به وجود آمدن ابهام، با نماد rad مشخص می‌شود. برای مثال، $$ 1.3 $$ رادیان را به صورت $$ 1.3 \, \mathrm { rad}$$ می‌نویسیم. تصویر متحرک زیر به خوبی تعریف یک رادیان را نشان می‌دهد.
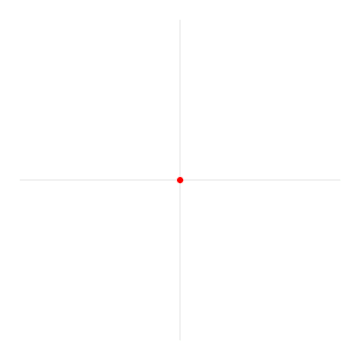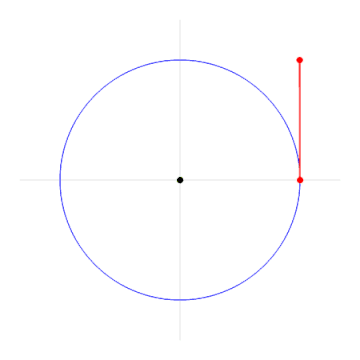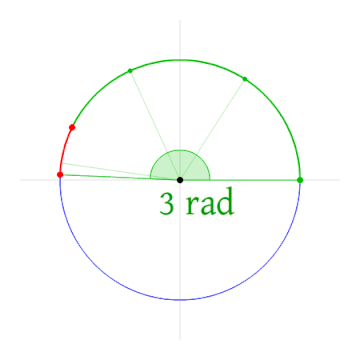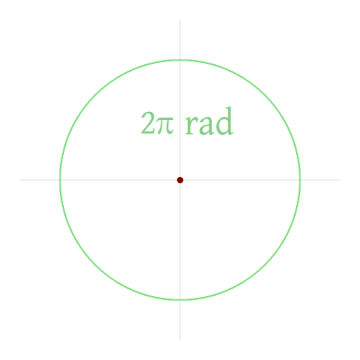
زاویه $$ 360 ^ \circ $$ متناظر با زاویه‌ای است که یک دایره کامل را گسترانیده و برابر با $$ 2 \pi $$ رادیان یا $$ 400$$ گرادیان است. یک رادیان، برابر با $$ 57.3 $$ درجه است. رادیان یک واحد پرکاربرد در ریاضیات است، زیرا با استفاده از آن، مشتق و انتگرال اتحادها را می‌توان به صورت جملات ساده نوشت.
تبدیل سایر واحدها به رادیان
با استفاده از جدول زیر می‌توان واحدهای مختلف اندازه‌گیری زاویه را به رادیان تبدیل کرد. برای مثال، اگر اندازه زاویه‌ای را برحسب درجه داشته باشیم، طبق جدول زیر، برای تبدیل آن به رادیان کافی است آن را در $$ \pi / 180 $$ یا $$ 0.01745329 $$ ضرب کنیم.
| تبدیل از | نماد واحد | تبدیل به | ضرب در | یا ضرب در |
| رادیان | rad | رادیان | $$ 1 $$ | $$ 1 $$ |
| درجه | $$ ^ \circ $$ | رادیان | $$\pi / 180 $$ | $$ 0.01745329 $$ |
| دقیقه | $$ ^ \prime $$ | رادیان | $$(\pi/180) / 60 $$ | $$ 2.908882 \times 10 ^ {-4}$$ |
| ثانیه | $$ ^ {\prime \prime}$$ | رادیان | $$(\pi / 180)/3600$$ | $$ 4.848137 \times 10 ^ {-6}$$ |
| اوکتانت | octant | رادیان | $$2 \pi / 8 $$ | $$0.7853982$$ |
| سکستانت |
sextant
| رادیان | $$2 \pi / 6 $$ | $$1.047196$$ |
| ربع | quadrant | رادیان | $$2 \pi / 4 $$ | $$1.570796$$ |
| دور یا چرخش | r | رادیان | $$2 \pi$$ | $$6.283185$$ |
| گرادیان | $$^ g $$ | رادیان | $$2\pi / 400$$ | $$0.01570796$$ |
| میلی‌رادیان | mil | رادیان | $$ 2 \pi / 64000$$ | $$ 9.817477 \times 10 ^ {-6}$$ |
درجه
درجه، یکی از واحدهای رایج اندازه‌گیری زاویه است. هر چرخش یا دور کامل یک دایره، برابر با $$ 360$$ درجه است.
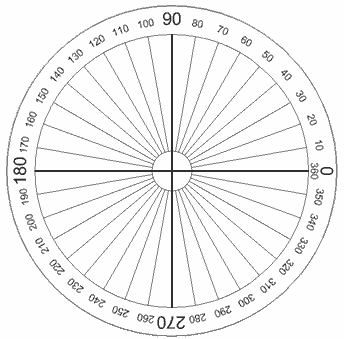
همچنین، زاویه برحسب درجه با نماد $$ ^ \circ$$ نشان داده می‌شود.
تبدیل سایر واحدها به درجه
با استفاده از جدول زیر می‌توان واحدهای مختلف اندازه‌گیری زاویه را به درجه تبدیل کرد. برای مثال، اگر اندازه زاویه‌ای را برحسب رادیان داشته باشیم، طبق جدول زیر، برای تبدیل آن به درجه کافی است آن را در $$ 180 / \pi $$ یا $$ 57.29578 $$ ضرب کنیم.
| تبدیل از | نماد واحد | تبدیل به | ضرب در | یا ضرب در |
| رادیان | rad | درجه | $$ 180 / \pi $$ | $$ 57.29578 $$ |
| درجه | $$ ^ \circ $$ | درجه | $$ 1 $$ | $$ 1 $$ |
| دقیقه | $$ ^ \prime $$ | درجه | $$ 1 / 60 $$ | $$ 0.016667 $$ |
| ثانیه | $$ ^ {\prime \prime}$$ | درجه | $$ 1 / 3600 $$ | $$ 2.777778 \times 10 ^ {-4}$$ |
| اوکتانت | octant | درجه | $$ 360 / 8 $$ | $$ 45 $$ |
| سکستانت | sextant | درجه | $$ 360 / 6 $$ | $$ 60 $$ |
| ربع | quadrant | درجه | $$ 360 / 4 $$ | $$90$$ |
| دور یا چرخش | r | درجه | $$ 360 / 1 $$ | $$360$$ |
| گرادیان | $$^ g $$ | درجه | $$ 360 / 400$$ | $$0.9$$ |
| میلی‌رادیان | mil | درجه | $$ 360 / 6400 $$ | $$0.05625$$ |
تبدیل واحد زاویه
درجه و رادیان از مهم‌ترین واحدهای بیان اندازه زاویه هستند و با استفاده از جدول‌هایی بالا می‌توان سایر واحدها را به آن‌ها تبدیل کرد. البته، با استفاده از جدول زیر می‌توان واحدهای مختلف اندازه‌گیری زاویه را به درجه تبدیل کرد.
برای مثال، اگر اندازه زاویه‌ای را برحسب رادیان داشته باشیم، طبق جدول زیر، برای تبدیل آن به درجه کافی است آن را در $$ 180 / \pi $$ یا $$ 57.29578 $$ ضرب کنیم.
| دور (r) | گرادیان ($$ ^ g $$) | ثانیه قوسی ($$ ^{\prime \prime}$$) | دقیقه قوسی ($$^ \prime$$) | درجه ($$^\circ$$) | میلی‌رادیان (mil) | رادیان (rad) | تبدیل از |
| $$ 0.159155$$ | $$ 63.661977$$ | $$ 206,265$$ | $$ 3,438$$ | $$ 57.29578$$ | $$ 1,000$$ | $$ 1 $$ | ۱ رادیان |
| $$ 0.000159$$ | $$ 0.063662$$ | $$ 206.264806$$ | $$ 3.437747$$ | $$ 0.057296$$ | $$ 1 $$ | $$ 0.001$$ | ۱ میلی‌رادیان |
| $$ 0.002778$$ | $$ 1.111111$$ | $$ 3,600$$ | $$ 60$$ | $$ 1 $$ | $$ 17.453293$$ | $$ 0.017453 $$ | ۱ درجه |
| $$ 0.000046296$$ | $$ 0.018519$$ | $$ 60 $$ | $$1$$ | $$ 0.016667$$ | $$ 0.290888$$ | $$ 0.000291$$ | ۱ دقیقه قوسی |
| $$ 0.0000007716$$ | $$ 0.000309$$ | $$ 1 $$ | $$ 0.016667$$ | $$ 0.000278$$ | $$ 0.004848$$ | $$ 0.0000048481$$ | ۱ ثانیه قوسی |
| $$ 0.0025$$ | $$ 1 $$ | $$ 3,240 $$ | $$ 54 $$ | $$ 0.9$$ | $$ 15.707963$$ | $$0.015708$$ | ۱ گرادیان |
| $$ 1 $$ | $$ 400$$ | $$ 1,296,000$$ | $$ 21,600$$ | $$ 360$$ | $$ 6,283$$ | $$6.283185$$ | ۱ دور |
| $$ 0.000156$$ | $$ 0.0625$$ | $$ 202.5$$ | $$ 3.375$$ | $$ 0.05625$$ | $$ 0.981748$$ | $$ 0.000982$$ | ۱ میل |
مثال‌های تبدیل واحد زاویه
در این بخش، چند مثال ساده را بررسی می‌کنیم.
مثال ۱
۹۰ گرادیان معادل با چند درجه است؟
حل: طبق جداول بالا، می‌دانیم که برای تبدیل گرادیان به درجه، آن را در $$0.9$$ ضرب کنیم. بنابراین:
$$ \large {90} ^ g = 90 \times 0.9 = 81 ^ \circ $$
در نتیجه، $$90$$ گرادیان برابر با $$ 81 $$ درجه است.
مثال ۲
چند دور معادله با ۵۰۰ درجه است؟
حل: برای تبدیل درجه به دور، به سادگی با استفاده از جدول بالا، داریم:
$$ \large 500 ^ \circ = 500 \times 0.002778 = 1.389\, \mathrm { r} $$
بنابراین، $$500 $$ درجه معادل با $$1.389 $$ دور است.
مثال ۳
۳۰ درجه، چند دقیقه قوسی است؟
حل: با توجه به جدول تبدیل واحد زاویه می‌بینیم که هر $$ 1 $$ درجه برابر با $$60 $$ دقیقه قوسی است. بنابراین، خواهیم داشت:
$$ \large 30 ^ \circ = 30 \times 60 = 1800 ^ \prime $$
در نتیجه، $$ 30 $$ درجه معادل با $$1800$$ دقیقه قوسی است.
اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:
اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:
- مجموعه آموزش‌های ریاضیات
- آموزش ریاضیات عمومی 1
- مجموعه آموزش‌های فیزیک
- آموزش فیزیک پایه ۱
- فرمول هرون — به زبان ساده
- زاویه داخلی و محاسبات آن در اشکال چندضلعی — به زبان ساده
- توان در فیزیک — به زبان ساده
^^
سلام 24/۴۵۳۳ معادل چند درجه و دقیقه و ثانیه می باشد
سلام
اگر اندازه سه ضلع یک مثلث را داشته باشیم و بخواهیم اندازه سه زاویه داخلی مثلث را بدست آوریم با فرمولهای موجود مانند ض ز ض با کمک مساحت و اندازه دو ضلع اندازه زاویه همیشه صحیح بدست نمی آید. بعنوان مثال اگر یکی از زوایای داخلی باز (منفرجه) باشد از طریق فرمول یاد شده اندازه صحیح بدست نمی آید چرا؟
اگه بخواهیم
11rad=چند درجه است؟ (۳۶۰_۰)
با سلام
بسیار زیبا و مفید و قابل فهم توضیح دادید. انشاالله موفق و سلامت باشید.
با سلام وسپاس فراوان
مطالب راجع به رادیان خیلی خیلی عالی توضیح داده بودید .
خداخیرتون بده.