زاویه، درجه و رادیان — به زبان ساده

یکی از واقعیتهای بدیهی این است که دایره 360 درجه دارد. آیا این واقعیت صحیح است؟ اغلب ما ایدهای از این که چرا دایره باید 360 درجه داشته باشد نداریم. ما یک عدد جادویی را به عنوان اندازه دایره به خاطر میسپاریم و این مسئله باعث میشود زمانی که به مطالعه ریاضیات یا فیزیکی پیشرفته با رادیان میپردازیم دچار مشکل شویم.
ریاضیدانها با دلایلی که ساده نیستند، توضیح میدهند که رادیانها باعث میشوند، ریاضیات سادهتر شود. در این نوشته به مفهوم واقعی رادیان و دلیل شهودی سادهتر شدن ریاضیات با استفاده از آنها میپردازیم. گرچه ریاضیدانها به این منظور از سری تیلور استفاده میکنند که خود ساده نیست!
درجه از کجا آمده است؟
ما پیش از اعداد و حتی زبان، ستارهها را داشتیم. تمدنهای باستانی از نجوم برای درک فصول سال، پیشبینی آینده و حتی راضی کردن خدایان استفاده میکردند (وقتی میخواستند انسانها را قربانی کنند، بهتر بود سر موقع این کار را انجام دهند!)
شاید بپرسید همه اینها چه ربطی به درجه دارند؟ آیا باعث شگفتی نیست که دایره 360 درجه دارد و هر سال نیز 365 روز دارد؟ آیا جای تعجب ندارد که صورتهای فلکی دایره 360 درجه آسمان را در طی 365 روز یک سال طی میکنند؟
البته امروزه اکثر شهرنشینان دیگر نمیتوانند فصول را از روی آسمان شب حدس بزنند. در تصویر زیر صورت فلکی دب اکبر را در آغاز فصلهای مختلف چنان که از آسمان شب تهران مشاهده میشود میبینید:
اگر حرکت صورتهای فلکی را هر شب دنبال کنید، میبینید که آنها نیز یک دایره در آسمان ترسیم میکنند. فرضیه این است که انسان نخستین بار متوجه شدند که صورتهای فلکی هر سال یک دایره کامل را در آسمان میپیمایند. هر روز آنها اندکی (یک درجه) جابجا میشوند. از آنجا که هر سال 360 روز دارد، بنابراین یک دایره نیز 360 درجه دارد.
اما اندکی صبر کنید ما میدانیم که هر سال 365 روز دارد و از این رو دایره نیز باید 365 درجه داشته باشد. اما باید توجه داشته باشید که انسانهای اولیه از ساعتهای آفتابی استفاده میکردهاند و احتمالاً راحت نبودهاند اگر یک سال 365.242199 درجه میداشت. 360 به عدد فوق نزدیک است و برای کارهای دیوانی نیز مناسب است. این عدد با سیستم اعداد بر مبنای 60 که در بابل رواج داشت نیز منطبق است و به راحتی بر اعداد 2، 3، 4، 6، 10، 12، 15، 30، 45، 90 بخشپذیر است. ریاضیات مقدماتی در مورد خورشید کاملاً معقول به نظر میرسد.
به نظر میرسد که عدد 360 برای تعداد روزهای سال عدد بسیار مناسبی است، اما باید بدانید که این عدد یک عدد قراردادی است. بر روی سیاره مریخ هر سال 680 روز دارد، چون مریخ روی دایره بزرگتری پیرامون خورشید میگردد. در برخی بخشهای اروپا نیز استفاده از گرادیان رواج دارد که در هنگام استفاده از آن هر دایره را باید به 400 بخش تقسیم کنید.
در بسیاری از نوشتهها میبینیم که وقتی به این نقطه میرسند، بیان میکنند که انتخاب درجه قراردادی بوده است و به هر حال باید یک عدد انتخاب میشد. اما مشاهده کردیم که انتخاب درجه مبنا و فلسفه خاصی داشته است.
رادیان فعال و درجه منفعل
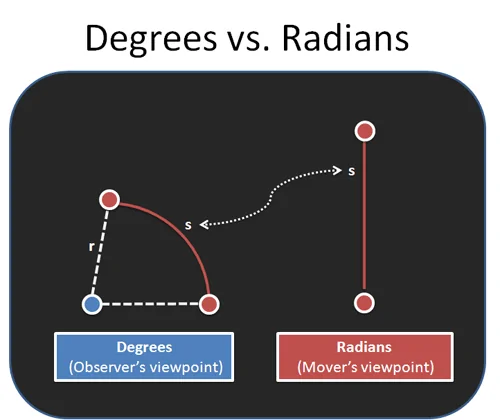
فرض کنید دوستتان روی یک دایره بزرگ در حال دویدن است و شما در مرکز دایره ایستادهاید. در این صورت درجه را میتوانیم به صورت میزان چرخشی که لازم است برای دیدن دوستتان سرتان را بچرخانید تعریف کنیم. در این حالت ممکن است دوستتان بگوید که واقعاً خسته شدم چون چند کیلومتر دویدهام، اما شما برای دیدن او کافی است اندکی (مثلاً 30 درجه) سر خود را بچرخانید.
میبینیم که درجه تا حد زیادی خودخواه است. ما معادلاتی مینویسیم که بدانیم باید چه مقدار سر خود را بچرخانیم تا ببینیم آن سیاره یا شیء متحرک از جای خود جابجا شده است. بدین ترتیب معادلات برای راحتی کار بیننده/ناظر تنظیم شدهاند.
رادیان: انتخاب غیر خودخواهانه
در اغلب بخشهای فیزیک (و حتی زندگی) باید قاب مرجع خود را ترک کنید و مسائل مختلف را از نقطه نظر دیگران ببینید. در مثال قبل به جای این که محاسبه کنیم چه قدر باید سر خود را بچرخانیم، میتوانیم محاسبه کنیم که دوستمان چه مقدار از مسیر دایره را طی کرده است.
در واقع درجه مقدار زاویه را بر حسب تغییر نسبت به ناظر اندازهگیری میکند؛ در حالی که رادیان زوایا را بر حسب مسافت پیموده شده اندازه میگیرد.
اما مسافت مطلق چندان مفید نیست، چون 10 کیلومتر بر حسب شعاع دایرهای که طی میشود میتواند دورهای مختلفی از دایره باشد. بنابراین این مسافت را بر شعاع دایره تقسیم میکنیم تا زاویه نرمال شدهای را به دست آوریم:
در اغلب موارد فرمول فوق را به صورت زیر میبینید:
به عبارت دیگر زاویه بر حسب رادیان (تتا) طول کمان (s) تقسیم بر شعاع (r) است.
هر دایره 360 درجه یا 2π رادیان دارد. اگر کل طول دایره را اندازهگیری کنیم، مقدار 2π * r / r به دست میآید. بنابراین هر رادیان در حدود مقدار زیر است:
360 / (2π) = 57.3 درجه
شاید با خود فکر کنید خب این هم یک واحد جدید است که برابر با 57.3 درجه است. اما نباید این گونه فکر کنید، چون هنوز در چارچوب درجه فکر میکنید و این خودخواهانه است!
وقتی گفته میشود حرکت به مقدار 1 رادیان بوده است، این عبارت به اندازه کافی گویا است و نیاز نیست آن را به درجه تبدیل کنید. برای قیاس تصور کنید کسی بگوید حرکت به اندازه 90 درجه گویا نیست و بهتر است آن را به صورت π /2 واحد بیان کنیم. برای مثال اگر به داستان دوستی که روی شعاع دایره میروید برگردیم فرض کنید از وی بخواهیم که 90 درجه بدود و وقتی متوجه نمیشود به او بگوییم که از نقطهای که تو ایستادهای باید π /2 دایره را طی کنی. در واقع هر دو آنها به اندازه کافی گویا هستند و بستگی به نقطه نظر گوینده یا شنونده دارند.
معنی لغوی رادیان چیست؟
رادیان واحد مسافت بر حسب واحد شعاع (radius) است و به نظرمی رسد که رادیان ترکیبی از آن کلمه باشد. به بیان سادهتر رادیان صرفاً یک عدد مانند 1.5 یا 73 است و هیچ واحدی ندارد. در محاسبات رادیان به معنی مسافت طی شده تقسیم بر شعاع دایره است و میبینیم که وقتی طول بر طول تقسیم میشود هر گونه واحدی از بین میرود. اما وقتی از دیدگاه عملی، رادیان را بررسی میکنیم بهتر است تصور کنیم که رادیان مسافت طی شده روی یک دایره واحد است.
استفاده از رادیان
اینک که با مفهوم رادیان آشنا شدیم، بهتر است مثال دوست دوندهمان را کمی بیشتر بررسی کنیم:
- ما وقتی میخواهیم سرعتهای چرخشی را اندازهگیری کنیم از «چرخش بر دقیقه» به جای «درجه بر ثانیه» استفاده میکنیم. در واقع این همان چرخش برای نگاه از دید دوست دونده است، گویی میخواهیم ببینیم وی چند دور دویده است و نیازی به معیار درجه نداریم.
- زمانی که یک ماهواره به دور زمین میگردد، سرعت آن را به صورت «کیلومتر بر ساعت» بیان میکنیم و نه «درجه بر ساعت». در این صورت اگر مسافت طی شده از سوی ماهواره را بر سرعت مداری تقسیم کنیم، سرعت آن بر حسب رادیان بر ساعت به دست میآید.
- سینوس، این تابع شگفتانگیز بر حسب رادیان به صورت زیر تعریف میشود:
این فرمول تنها زمانی صدق میکند که x بر حسب رادیان باشد. دلیل این مسئله آن است که سینوس اساساً به مسافت طی شده ارتباط دارد و نه میزان چرخش سر!
مثال اول برای رادیان: چرخهای اتوبوس
در این بخش یک مثال خیالی را بررسی میکنیم. فرض کنید شما یک اتوبوس دارید که چرخهای آن 2 متر شعاع دارند. بدیهی است که چنین اتوبوسی باید بسیار عظیمالجثه باشد، اما این فقط یک مثال است. اگر کسی به شما بگوید که چرخهای این اتوبوس با چه سرعتی میچرخند، شما میتوانید سرعت حرکت اتوبوس را محاسبه کنید. برای نمونه فرض کنید سرعت گردش چرخهای اتوبوس 2000 درجه بر ثانیه باشد.

اینک میتوانیم بینیم که حرکت به میزان 2000 درجه بر ثانیه یعنی چرخها در هر ثانیه 2000/360 یا 5 و 5/9 دور میزنند. محیط چرخها برابر با 2π * r است و از این رو
2 × 3.14 × 2 × 5.56 = 69.83 متر بر ثانیه
اینک تصور کنید خودرویی با چرخهایی به شعاع 2 متر دارید که چرخهای خودرو با سرعت 6 رادیان بر ثانیه میگردند. اینک میتوان تصور کرد که رادیان مسافت طی شده در راستای یک دایره واحد است و میتوان آن را به مقیاس شعاع واقعی درآورد. بنابراین 6 * 2 = 12 متر بر ثانیه. میبینید که محاسبه چه قدر آسان بود.
در دو مثال فوق دیدیم که محاسبه سرعت خودرو بسیار آسانتر از سرعت اتوبوس است. هیچ فرمول عجیب و غریبی وجود ندارد و نیازی به استفاده از عدد پی نیز وجود ندارد. کافی است سرعت زاویهای را در مقیاس مناسب ضرب کنید تا سرعت خطی به دست آید. همه اینها به این دلیل است که رادیان به محاسبه مسافت از دید متحرک میپردازد.
عکس محاسبه فوق نیز آسان است. فرض کنید با سرعت 30 متر بر ثانیه (108 کیلومتر بر ساعت) در یک بزرگراه رانندگی میکنید و شعاع تایرهای خودرو شما هم 30 سانتیمتر است. اینک سؤال این است که سرعت گردش تایرها چه مقدار است؟
با تقسیم سرعت 30 متر بر ثانیه بر شعاع 30 سانتیمتری (0.3 متر) میبینیم که عدد 100 رادیان بر ثانیه برای سرعت گردش تایرها به دست میآید.
مثال دوم رادیان: (Sin (x
اینک نوبت مثال عمیقتری رسیده است. در حسابان چیزهای مختلفی بررسی میشود. یکی از مهمترین مباحثی که در حسابان بررسی میشود، حساب مقادیر بسیار بزرگ یا بسیار کوچک است.
یک عدد برای درجه (x) انتخاب کنید و (Sin(x را در ماشین حساب به دست آورید:
زمانی که x عدد کوچکی مانند 0.1 انتخاب شود، (Sin(x نیز کوچک خواهد بود. و نسبت Sin(x)/x در حدود 0.017 است. این به چه معنی است؟ و چه ارتباطی با ضرب یا تقسیم در یک درجه دارد؟ آیا میتوان درجات مربع یا حتی مکعب داشت؟
رادیان راهحل نجات است. میدانیم که رادیانها به مسافت پیموده شده روی دایره مربوط هستند و بنابراین معادله را میتوانیم به صورت زیر تفسیر کنیم:
- X مقدار مسافت پیموده شده روی یک دایره است
- (Sin(x میزان ارتفاعی است که روی دایره کسب کردهاید.
بنابراین Sin(x)/x برابر است با نسبت میزان مسافت طی شده بر مقدار انرژی پتانسیلی که در جهت رو به بالا کسب کردهاید. اگر به صورت عمودی حرکت کنید، این نسبت 100% است. اگر افقی حرکت کنید این نسبت 0% است.
زمانی که چیزی از دید ما مقدار کمی مثلاً 0 تا 1 درجه حرکت میکند، این حرکت عمودی خواهد بود. اگر این حرکت از این هم کوچکتر مثلاً از 0 تا 0.00001 درجه باشد، این حرکت باز هم به خط قائم نزدیکتر میشود. چون مسافت پیموده شده (x) بسیار به ارتفاع (Sin(x نزدیک است.
با کاهش x این نسبت به 100% نزدیک میشود. چون حرکت عمودیتر میشود. رادیان کمک میکند که به طور شهودی ببینیم چرا Sin(x)/x با کوچک شدن x به 1 نزدیک میشود. چون ما در واقع در مسافت اندکی به سمت بالا حرکت کردهایم. بدین ترتیب این واقعیت توضیح میدهد که چرا برای اعداد کوچک sin(x) ~ x است.
بدیهی است که شما میتوانید این وضعیت را با استفاده از حسابان اثبات کنید؛ اما کسب بینش شهودی در مورد رادیان کمک میکند که آن را بهتر درک کنید.
به خاطر داشته باشید که این رابطهها تنها زمانی صدق میکنند که زاویهها را با رادیان اندازهگیری کنید در مورد درجه اگر میزان ارتفاع روی دایره (Sin(x را با مسافت پیموده شده (x) مقایسه کنید سرعت تغییرات بالاتر خواهد بود.
سخن پایانی
درجه جایگاه خاص خود را در زندگی روزمره ما دارد، چون ما در اغلب موارد خود را نقطه کانونی میبینیم و میخواهیم ببینیم چگونه اشیای مختلف بر ما تأثیر میگذارند. چه مقدار باید تلسکوپ خود را بالاتر ببریم؟ اسنوبرد خود را با چه زاویهای بگیریم و آیا باید فرمان خودرویمان را بچرخانیم یا نه.
به طور طبیعی ما یک شاهد هستیم که حرکت چیزهای دیگر را توصیف میکنیم. رادیان در مورد چیزهای دیگری است که حرکت میکنند و نه ما. برخی افراد برای درک همین نکته، سالها از عمر خود را صرف میکنند.
درجه واحدی قراردادی است، زیرا بر مبنای خورشید (365 روز ~ 360 درجه) تنظیم شده است؛ اما یکایی جانبی محسوب میشود، زیرا از نقطه نظر ناظر اندازهگیری میشود.
از طرف دیگر رادیان بر حسب شیء متحرک است و اعمال معادلات بر حسب آن آسان است. همان طور که دیدیم به سادگی میتوان با استفاده از رادیان سرعت زاویهای را به سرعت خطی تبدیل کرد و ایدههایی مانند Sin(x)/x تنها با استفاده از رادیان معنی مییابند.
حتی به زاویهها نیز میتوان از بیش از یک نقطه نظر نگریست. درک رادیانها باعث میشود که معادلههای ریاضیات و فیزیک شهودیتر باشند.




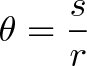
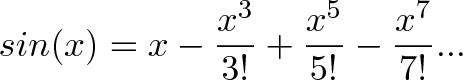












سلام درمتن یک غلط املایی وجود داره که اصلاح کنید
قطر تایر اتوبوس نیست، شعاع تایر اتوبوس هست که اصلاح شود
سلام و وقت بخیر؛
متن مقاله اصلاح شد. ممنون از دقت نظر شما.
از همراهیتان با مجله فرادرس سپاسگزاریم.
خوبه، دبیرمون گفته بود نفهمیده بودم 🙁
عالی .بینظیر .درجه یک .دمتون گرم و پاینده باشین 😘😘😘😘😘
بهترین توضیحی که میشه از رادیان پیدا کرد.خیلی ممنون از سایت خوبتون
با سلام.اول از همه من دانش آموز کلاس هفتم هستم و اطلاعات چندانی از مسائل پایه های بالاتر ندارم ،بجز اندکی تحقیقاتی که انجام میدم..موضوعی منجر به درگیری ذهنم شده .کره ای رو تصور کنید و اون رو به قسمت های مساوی تقسیم کنید .(تعداد قسمت ها مهم نیست)بعد از انجام این کار کره رو در جهت دیگه به دو نصف تقسیم کنید..حال دقیقا وسط سطح قسمت های اولی که تقسیم کرده بودیم با مقداری از محیط دایره معکوس برابر است ،البته اگر اشتباه نکنم .چطور میتوانیم اون مقدار رو بدست بیاریم؟ فکر کردم که شاید بشه از درجه کمک گرفت اما هیچ اطلاعاتی نداشتم و این مسئله بی نتیجه موند.ممنون میشم اگر شما که اطلاعات دارید راهنماییم کنید چون این سوال به موضوعی مهم تر ختم میشه و من به فهمیدنش احتیاج دارم .ممنون از شما
سلام.
توجه کن که برای پیدا کردن وسط اشکال نامتعارف باید شکل رو داخل یک دایره قرار بدی یا اصطلاحاً اون شکل رو روی دایره محاط کنی،وسط دایره میشه وسط شکلت
حالا من کاملا متوجه نشدم منظورت از مقدار چیه، چون وسط یک شکل سه بعدی یک نقطه هست و یک نقطه مقدار نداره اصطلاحاً دارای مؤلفه های طول و عرض و ارتفاع هستش. اگه علاقه مندی پیشنهاد میکنم مبحث انتگرال رو مطالعه کنی بهت کمک میکنه البته اگه قبلش با مشتق و تابع آشنا هستی. موفق باشی
فک کنم بهتره بجای مسافت از جابجایی استفاده کنیم
مسافت امکان داره کیلومتر ها باشه
اما جابجایی از محیط کمتره همیشه و منطقی تر درمیاد
سلام
اینجا منظور از مسافت پیموده شده،در واقع حرکت بر روی محیط دایره است و در واقع منظور برآیند حرکت که برابر وتر دایره است لحاظ نمی شود.