اتحاد مزدوج چیست؟ — فرمول، اثبات، مثال و حل تمرین

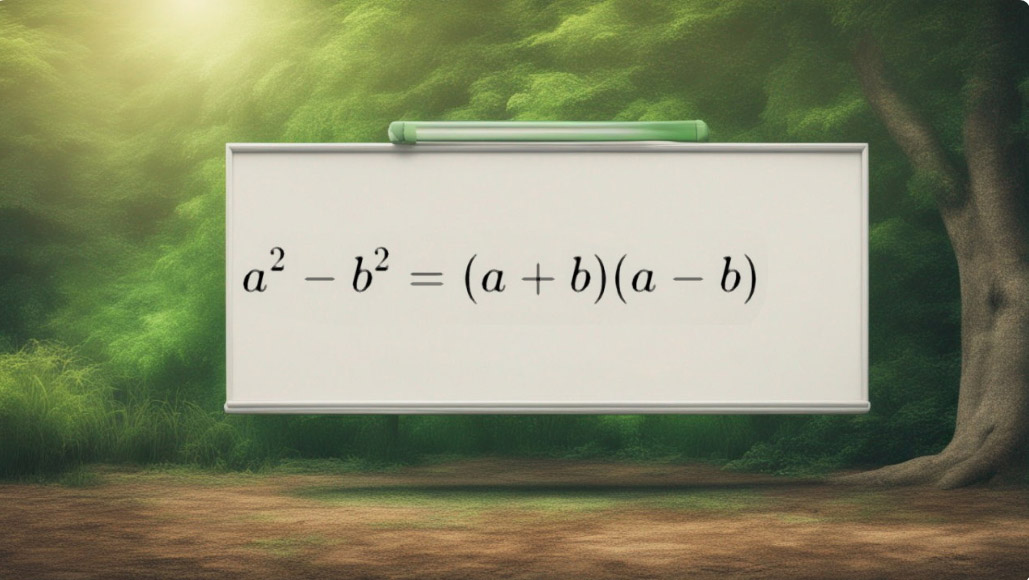
در آموزش‌های پیشین مجله فرادرس، با اتحاد و تجزیه در ریاضی آشنا شدیم. همچنین، برخی از اتحادها، مانند اتحاد مکعب دوجمله‌ای، اتحاد مکعب و اتحاد چاق و لاغر را معرفی کردیم و در مطلبی به حل نمونه سؤالات اتحاد و تجزیه پرداختیم. اتحاد مزدوج یکی از رایج‌ترین اتحادهای جبری است که در این آموزش مطالبی را درباره آن بیان می‌کنیم.

اتحاد مزدوج چیست ؟

اتحاد مزدوج یا «تفاضل دو مربع» (Difference of Two Squares) یک تساوی است که در یک طرف آن تفاضل دو جمله مربع وجود دارد و در طرف دیگر آن، حاصل‌ضرب دو عبارت.

فرمول اتحاد مزدوج به این صورت است:

$$ \large \color {blue} { { a } } ^ 2 – \color {green} { { b } } ^ 2 = ( \color {blue} { a } + \color {green} { b } ) ( \color {blue}{ a } – \color {green} { b } ) $$

اثبات اتحاد مزدوج

می‌خواهیم تساوی زیر را اثبات کنیم:

$$ \large ( a + b ) ( a – b ) = a ^ 2 – b ^ 2 $$

سمت چپ تساوی را می‌توان به‌صورت زیر نوشت:‌

$$ \large \begin {aligned} ( a + b ) ( a – b ) & = a ( a – b ) + b ( a – b ) \\ & = a ^ 2 – a b + a b – b ^ 2 \\ & = a ^ 2 – b ^ 2 \end{aligned} $$

می‌بینیم که سمت چپ تساوی با سمت راست برابر است و اثبات کامل می‌شود.

برای آشنایی با مباحث ریاضیات مدرسه، پیشنهاد می‌کنیم به «مجموعه آموزش‌های دروس دبیرستان و پیش دانشگاهی» فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه آموزش‌های دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.

تعبیر هندسی اتحاد مزدوج

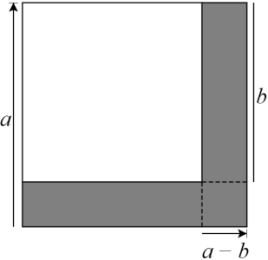
اتحاد مزدوج را می‌توان به‌‌صورت هندسی با تفاضل مساحت دو مربع بیان کرد. در شکل زیر، بخش‌های سایه‌دار اختلاف مساحت‌های دو مربع، یعنی $$ a ^ 2 – b ^ 2 $$ را نشان می‌دهند. مساحت این ناحیه را می‌توان با جمع مساحت دو مستطیل نیز به‌دست آورد: $$ a ( a – b ) + b ( a – b ) $$. اگر در عبارت اخیر از فاکتورگیری استفاده کنیم، به $$ ( a+ b ) ( a -b ) $$ می‌رسیم. بنابراین، $$a^2 – b^2 = (a+b)(a-b)$$.

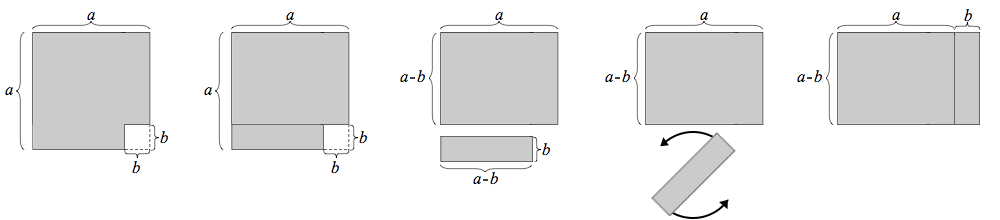
اثبات هندسی دیگری نیز می‌توان بیان کرد. از تصویر سمت چپ شکل زیر شروع می‌کنیم؛ یک مربع بزرگ که مربع کوچک‌تری از آن جدا شده است. اندازه ضلع مربع $$a$$ است و ضلع مربع کوچک حذف‌شده $$b$$ است. مساحت ناحیه‌ سایه‌دار $$ a ^ 2 – b ^ 2 $$ است.

همان‌طور که در شکل دوم از چپ نشان داده شده است، یک برش ایجاد می‌شود و ناحیه را به دو قطعه مستطیلی تقسیم می‌کند. قطعه بزرگ‌تر، در بالا، دارای عرض $$a$$ و ارتفاع $$a-b$$ است. قطعه کوچک‌تر، در پایین، دارای عرض $$a-b$$ و ارتفاع $$b$$ است. اکنون می‌توان قطعه کوچک‌تر را جدا کرد، چرخاند و در سمت راست قطعه بزرگ‌تر قرار داد. در این چیدمان جدید، که در آخرین تصویر نشان داده شده است، دو قطعه با هم مستطیلی را تشکیل می‌دهند که عرض آن $${\displaystyle a+b}a+b$$ و ارتفاع آن $${\displaystyle a-b}a-b$$ است. مساحت این مستطیل $${\displaystyle (a+b)(a-b)}(a+b)(a-b)$$ است. از آنجا که این مستطیل از چیدمان مجدد شکل اصلی به‌وجود آمده است، باید مساحت آن برابر با شکل اصلی باشد. بنابراین، $${\displaystyle a^{2}-b^{2}=(a+b)(a-b)}a^2-b^2 = (a+b)(a-b)$$.

کاربردهای اتحاد مزدوج

در این بخش، به برخی از کاربردهای اتحاد مزدوج اشاره می‌کنیم.

فاکتورگیری از چندجمله‌ای‌ها و ساده‌سازی عبارات

فرمول اتحاد مزدوج را می‌توان برای فاکتورگیری چندجمله‌ای‌هایی که شامل مربع یک کمیت منهای مربع یک کمیت دیگر هستند به‌کار برد. به‌عنوان مثال، از چندجمله‌ای $$x^4 – 1$$ می‌توان به‌صورت زیر فاکتور گرفت:

$$ \large x ^ 4 – 1 = ( x ^ 2 + 1 ) ( x ^ 2 – 1 ) = ( x ^ 2 + 1 ) ( x + 1 ) ( x – 1 ) $$

به‌عنوان مثال دوم، دو جمله اول $$ { \displaystyle x ^ { 2 } – y^ { 2 } + x – y } $$ را می‌توان به‌‌صورت $$ { \displaystyle ( x + y ) ( x – y ) } $$ نوشت. بنابراین داریم:

$$ \large x^2 – y^2 + x – y = (x + y)(x – y) + x – y = (x – y)(x + y + 1) $$

علاوه بر این، فرمول را می‌توان برای ساده‌سازی عبارات استفاده کرد. برای مثال، عبارت زیر با این اتحاد ساده شده است:

$$ \large { \displaystyle ( a + b ) ^ { 2 } – ( a – b ) ^ { 2 } \\ \large =( a + b + a – b ) ( a + b – a + b ) \\ \large = ( 2 a ) ( 2 b ) = 4 a b } $$

اعداد مختلط: جمع دو مربع

از اتحاد مزدوج برای یافتن عامل‌های خطی مجموع دو مربع با استفاده از ضرایب اعداد مختلط استفاده می‌شود. برای مثال، ریشه‌های مختلط $${\displaystyle z^{2}+4}{\displaystyle z^{2}+4}$$ را می‌توان با استفاده از اتحاد مزدوج پیدا کرد:

$$ \large { \displaystyle z ^ { 2 } + 4 }
{ \displaystyle = z ^ { 2 } – 4 i ^ { 2 } } \\
\large { \displaystyle = z ^ { 2 } – ( 2 i ) ^ { 2 } }
{ \displaystyle = ( z + 2 i ) ( z – 2 i ) } $$

بنابراین، عامل‌های خطی $$ (z + 2 i ) $$ و $$ ( z – 2 i ) $$ هستند.

از آنجا که دو عامل به‌دست‌آمده از این روش مزدوج مختلط هستند، می‌توانیم از این روند به‌صورت معکوس به‌منظور روشی برای ضرب یک عدد مختلط و به‌دست آوردن یک عدد حقیقی استفاده کنیم. این روش برای به‌دست آوردن مخرج حقیقی در کسرهای مختلط استفاده می‌شود.

گویا کردن مخرج‌ها

از اتحاد مزدوج می‌توان برای گویا کردن مخرج‌های غیرگویا نیز استفاده کرد. این روشی برای حذف ریشه‌ها از عبارات (یا حداقل جابه‌جایی آن‌ها) است، که برای تقسیم با برخی از ترکیبات شامل ریشه‌های مربع اعمال می‌شود. برای مثال، مخرج $$ { \displaystyle { \dfrac { 5 } { { \sqrt { 3 } } + 4 } } } $$ را می‌توان به‌صورت زیر گویا کرد:

$$ \large \dfrac { 5 } { \sqrt { 3 } + 4 } = \dfrac { 5 } { \sqrt { 3 } + 4 } \times \dfrac { \sqrt { 3 } – 4 } { \sqrt { 3 } – 4 } \\ \large = \dfrac { 5 ( \sqrt { 3 } – 4 ) } { ( \sqrt { 3 } + 4 ) ( \sqrt { 3 } – 4 ) } = \dfrac { 5 ( \sqrt { 3 } – 4 ) } { \sqrt { 3 } ^ 2 – 4 ^ 2 } \\ \large = \dfrac { 5 ( \sqrt { 3 } – 4 ) } { 3 – 16 } = – \dfrac { 5 ( \sqrt { 3 } – 4 ) } { 1 3 } . $$

محاسبات ذهنی

از اتحاد مزدوج می‌توان به‌عنوان یک میانبر برای محاسبه نیز استفاده کرد. اگر دو عدد (که میانگین آن‌ها عددی است که به‌راحتی مجذور می‌شود) در هم ضرب شوند، می‌توان اتحاد مزدوج را برای به‌دست آوردن حاصل‌ضرب دو عدد اصلی به‌کار برد. برای مثال، $$ 27 \times 33 = (30 – 3)(30 + 3) $$ را در نظر بگیرید. با استفاده از اتحاد مزدوج، $$ 27 \times 33 $$ را می‌توان به‌صورت زیر محاسبه کرد:‌

$$ \large 30^2 – 3^2 = 891. $$

تفاوت دو مربع کامل متوالی

تفاضل دو مربع کامل متوالی حاصل‌جمع دو پایه $$n$$ و $$n+1$$ است:

$$ \large \begin {array} {lcl}
( n + 1 ) ^ 2 – n ^ 2 & = & ( ( n + 1 ) + n ) ( ( n + 1 ) – n ) \\
& = & 2 n + 1
\end {array} $$

بنابراین، اختلاف دو مربع کامل متوالی یک عدد فرد است. به‌طور مشابه، اختلاف دو مربع کامل دلخواه به‌صورت زیر محاسبه می‌شود:

$$ \large \begin {array} {lcl}
( n + k ) ^ 2 – n ^ 2 & = & ( ( n + k ) +n ) ( ( n + k ) – n ) \\
& = & k ( 2 n + k )
\end {array} $$

در نتیجه، تفاضل دو مجذور زوج کامل مضرب 4 و تفاضل دو مربع کامل فرد مضرب 8 است.

فاکتورگیری از اعداد صحیح

چندین الگوریتم در نظریه اعداد و رمزنگاری وجود دارند که در آن‌ها از اتحاد مزدوج برای یافتن عامل‌های اعداد صحیح و تشخیص اعداد مرکب استفاده می‌شود. یک مثال ساده روش تجزیه فرما است که دنباله اعداد $$x_i:=a_i^2-N$$ را برای $$a_i:=\left\lceil \sqrt{N}\right\rceil+i$$ در نظر می‌گیرد. اگر یکی از $$x_i$$ها برابر با مربع کامل $$b^2$$ باشد، آنگاه $$N=a_i^2-b^2=(a_i+b)(a_i-b)$$ یک عامل‌گیری یا فاکتورگیری از $$N$$ است.

مثال‌های اتحاد مزدوج

در این بخش، چند مثال را از اتحاد مزدوج بیان می‌کنیم.

مثال اول اتحاد مزدوج

عبارت $$ 5 ^ 2 – 2 ^ 2 $$ را به‌‌صورت یک حاصل‌ضرب بازنویسی کنید.

حل: از اتحاد مزدوج کمک می‌گیریم و خواهیم داشت:

$$ \large 5 ^ 2 – 2 ^ 2 = ( 5 – 2 ) \times ( 5 + 2 ) = 3 \times 7 . $$

مثال دوم اتحاد مزدوج

حاصل ضرب $$ 299 \times 301 $$ را محاسبه کنید.

حل: می‌توانیم با استفاده از ماشین‌حساب به این مسئله پاسخ دهیم، اما راه شیرین‌تری داریم که در این آموزش آن را فراگرفته‌ایم؛ بنابراین از اتحاد مزدوج استفاده می‌کنیم. می‌دانیم که $$ 299=300-1$$ و $$ 301=300+1$$. بنابراین، داریم:

$$ \large \begin {aligned} 299 \times 301 & = ( 300 – 1 )( 300 + 1 ) \\ & = 300 ^ 2 – 1 ^ 2 \\ & = 89999. \ \end {aligned} $$

مثال سوم اتحاد مزدوج

نشان دهید هر عدد فرد را می‌توان به‌صورت تفاضل دو مربع نوشت.

حل: عدد فرد را به‌‌صورت $$ n = 2 b + 1 $$ درنظر می‌گیریم که در آن، $$ b $$ یک عدد صحیح نامنفی است. داریم:

$$ \large n = 2 b + 1 = [ ( b + 1 ) + b ] [ ( b + 1 ) – b ] = ( b+ 1 )^ 2 – b ^ 2 . $$

مثال چهارم اتحاد مزدوج

حاصل عبارت زیر را به‌دست آورید:

$$ \large 234567 ^ 2 – 234557 \times 234577 $$

حل: با استفاده از اتحاد مزدوج، می‌توان مقدار این عبارت را به‌سادگی محاسبه کرد:

$$ \large \begin {aligned} 234567 ^ 2 – 234557 \times 234577 & = 234567 ^ 2 – \big ( 234567 ^ 2 – 10 ^ 2 \big ) \\ & = 234567 ^ 2 – 234567 ^ 2 + 10 ^ 2 \\ & = 100 . \end {aligned} $$

مثال پنجم اتحاد مزدوج

عبارت زیر را ساده کنید:

$$ \large \left ( 1 – \frac { 1 } { 2 ^ 2 } \right ) \left ( 1 – \frac { 1 } { 3 ^ 2 } \right ) \left ( 1 – \frac { 1 } { 4 ^ 2 } \right ) \cdots \left ( 1 – \frac { 1 } { n ^ 2 } \right ) . $$

حل: این مثال یک کاربرد بسیار مستقیم از اتحاد مزدوج است. داریم:

$$ \large \begin {aligned} \left ( 1 – \frac { 1} { 2^ 2 } \right ) \left ( 1 – \frac { 1 } { 3 ^ 2 } \right ) \cdots \left ( 1 – \frac { 1 } { n ^ 2 } \right) & = \left ( 1 – \frac { 1 } { 2 } \right ) \left ( 1 + \frac { 1 } { 2 } \right ) \left ( 1 – \frac { 1 } { 3 } \right ) \left ( 1 + \frac { 1 } { 3 } \right ) \cdots \left ( 1 – \frac { 1 } { n } \right ) \left ( 1 + \frac { 1 } { n } \right ) \\ & = \frac { 1 } { 2 } \cdot \frac { 3 } { 2 } \cdot \frac { 2 } { 3 } \cdot \frac {4 }{ 3 } \cdots \frac { n – 1 } { n } \cdot \frac { n + 1} { n } . \end {aligned} $$

دقت کنید که ضرب جمله دوم در جمله $$(n-1)$$اُم برابر با ۱ است و در نتیجه، ضرب نهایی $$ \frac { n + 1 } { 2 n } $$ است.

مثال ششم اتحاد مزدوج

عبارت زیر را ساده کنید:

$$ \large \left ( \sqrt 5+ \sqrt 6 + \sqrt 7 \right ) \left ( \sqrt 5 + \sqrt 6 – \sqrt 7 \right ) \left ( \sqrt 5 – \sqrt 6 + \sqrt 7 \right ) \left ( – \sqrt 5 + \sqrt 6 + \sqrt 7 \right ) . $$

انتخاب نخست، اما سخت، می‌تواند این باشد که عبارت را گسترش دهیم. اما این کار زمان‌بر است و بسیار مستعد خطا. بنابراین، از اتحاد استفاده می‌کنیم و داریم:

$$ \large \begin {aligned} \big ( \sqrt 5 + \sqrt 6 + \sqrt 7 \big ) \big ( \sqrt 5 + \sqrt 6 – \sqrt 7 \big ) & = \big ( \sqrt 5 + \sqrt 6 \big ) ^ 2 – \big ( \sqrt 7 \big ) ^ 2 \\ & = 5 + 6 + 2 \sqrt { 3 0 } – 7 \\ & = 4 + 2 \sqrt {30} . \end {aligned} $$

به همین ترتیب، حاصل‌ضرب دو عبارت آخر به‌‌صورت زیر است:

$$ \large \begin {aligned} \big ( \sqrt 5 – \sqrt 6 + \sqrt 7 \big ) \big ( – \sqrt 5 + \sqrt 6 + \sqrt 7 \big) & = \left ( \sqrt 7 + \big ( \sqrt 5 – \sqrt 6 \big ) \right ) \left ( \sqrt 7 – \big ( \sqrt 5 – \sqrt 6 \big ) \right ) \\ & = – 4 + 2 \sqrt { 3 0 } . \end {aligned} $$

ضرب نهایی نیز به‌صورت زیر است:

$$ \large \left ( 4 + 2 \sqrt { 3 0 } \right ) \left ( – 4 + 2 \sqrt { 3 0 } \right ) = 4 ( 3 0 ) – 1 6 = 1 0 4 . $$

تعمیم اتحاد مزدوج

در این بخش‌، به برخی از تعمیم‌هایی که می‌توان ببرای اتحاد مزدوج بیان کرد اشاره می‌کنیم.

اتحاد مزدوج و ضرب داخلی

اتحاد مزدوج در فضاهای ضرب داخلی روی میدان اعداد حقیقی، مانند حاصل‌ضرب نقطه‌ای بردارهای اقلیدسی نیز قابل بیان است:

$$ \large { \displaystyle { \mathbf { a } } \cdot { \mathbf { a } } – { \mathbf { b } }\cdot { \mathbf { b } } = ( { \mathbf { a } } +{ \mathbf { b } } ) \cdot ( { \mathbf { a } } – { \mathbf { b } } ) } $$

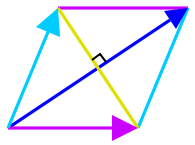
برای حالت خاصی که $$\mathbf { a }$$ و $$\mathbf { b }$$ نرم‌های مساوی دارند (به این معنی که مربع‌های نقطه‌ای آن‌ها مساوی است)، به‌صورت تحلیلی می‌توان نشان داد که دو قطر یک لوزی عمود بر هم هستند. بنابراین، سمت چپ معادله برابر با صفر است و باید سمت راست نیز برابر با صفر باشد. به همین دلیل، مجموع برداری $$\mathbf { a+b }$$ (قطر بلند لوزی) با تفاضل برداری $$\mathbf { a-b }$$ (قطر کوتاه لوزی) باید برابر با صفر باشد، که نشان می‌دهد قطرها عمود هستند.

در شکل زیر، بردار $$\mathbf { a }$$ (بنفش)، بردار $$\mathbf { b }$$ (فیروزه‌ای) و بردار $$\mathbf { a+b }$$ (آبی) نشان داده شده است.

حاصل‌ضرب دو تفاوت دو مربع خود اختلاف دو مربع به دو صورت متفاوت است:

اتحاد مزدوج برای توان n

اگر $$ a $$ و $$ b $$ دو مؤلفه از حلقه جابه‌جایی $$R$$ باشند، آن‌گاه:

$$ \large { \displaystyle a ^ { n } – b ^ { n } = \left ( a – b \right ) \left ( \sum _ { k = 0 } ^ { n – 1 } a ^ { n – 1 – k } b ^ { k } \right ) } . $$

حاصل‌ضرب دو تفاضل دو مربع

حاصل‌ضرب دو تفاضل دو مربع، به‌صورت زیر خواهد بود:

$$ \large \begin {array} { l l l } \left ( a ^ 2 – b ^ 2 \right ) \left ( c ^ 2 – d ^ 2 \right ) & = ( a c ) ^ 2 – ( a d ) ^ 2 – ( b c ) ^ 2 +( b d ) ^ 2 \\ & = ( a c ) ^ 2 – ( a d ) ^2 – ( b c ) ^ 2 +( b d ) ^ 2 + 2 a b c d – 2 a b c d \\ & = ( a c ) ^ 2 + 2 a b c d + ( b d ) ^ 2 -\left[ ( a d ) ^ 2 + 2 a b c d +( b c ) ^ 2 \right] & = ( a c + b d ) ^ 2 – ( a d + b c ) ^ 2 \\ & = ( a c ) ^ 2 – 2 a b c d + ( b d ) ^ 2 – \left[ ( a d ) ^ 2 – 2 a b c d + ( b d ) ^ 2 \right] & = ( a c – b d ) ^ 2 – ( a d – b c ) ^ 2 . \\ \end{array} $$

معرفی فیلم آموزش ریاضی و آمار (۱) – پایه دهم علوم انسانی

یکی از آموزش‌های ویدیویی دوره دبیرستان فرادرس، «آموزش ریاضی و آمار (۱) – پایه دهم علوم انسانی» است که به طور ویژه مربوط به دانش‌آموزان رشته علوم انسانی است. این آموزش ویدیویی در قالب چهار درس و در زمان ۶ ساعت و ۱۹ دقیقه تدوین شده است. در درس یکم، معادله درجه دوم مورد بحث قرار گرفته که شامل مطالب اصلی درس، نکات مهم و مثال‌های حل شده است. در درس دوم، موضوع مهم تابع ارائه شده و در آن، به موارد مهمی از قبیل تعریف ضابطه و تابع، رسم آن، دامنه و برد تابع و… پرداخته شده است. کار با داده‌های آماری موضوع درس سوم است. در نهایت، در درس چهارم به طور کامل، مطالب کتاب درسی درباره نمایش داده‌ها ارائه شده است.

• برای مشاهده فیلم آموزش ریاضی و آمار (۱) – پایه دهم علوم انسانی + اینجا کلیک کنید.

معرفی فیلم آموزش ریاضی پایه دانشگاهی

یکی از آموزش‌هایی که برای آشنایی بیشتر با مبحث اتحاد و تجزیه می‌توانید به آن مراجعه کنید، آموزش ریاضی پایه دانشگاهی است. این آموزش که مدت آن ۱۲ ساعت و ۴۶ دقیقه است، در قالب ۱۰ درس تهیه شده است.

در درس اول، مجموعه‌ها، مجموعه اعداد، توان، ب.م.م و ک.م.م معرفی شده‌اند. موضوعات درس دوم، چندجمله‌ای‌ها و اتحاد و تجزیه است. در درس سوم، نامساوی‌ها، نامعادلات، طول پاره‌خط، ضریب زاویه و معادله خط مورد بحث قرار گرفته‌اند. مثلثات موضوع مهم درس چهارم است. تصاعد حسابی و هندسی در درس پنجم بررسی شده‌اند. تابع و دامنه و برد آن موضوعات مهم درس ششم هستند. در درس هفتم، تساوی دو تابع، اعمال جبری روی تابع و ترکیب توابع ارائه شده‌اند. در درس هشتم به توابع زوج و فرد، تابع یک به یک و تابع وارون پرداخته شده است. انواع توابع از قبیل تابع ثابت، تابع همانی، تابع علامت، تابع قدر مطلق و تابع جزء صحیح موضوع درس نهم هستند. در نهایت، در درس دهم توابع نمایی و لگاریتمی مورد بحث قرار گرفته‌اند.

• برای مشاهده فیلم آموزش ریاضی پایه دانشگاهی + اینجا کلیک کنید.