فرادرس
قدر نسبت دنباله هندسی | فرمول محاسبه با مثال — به زبان ساده
در ریاضیات، دنباله‌ها به همراه جمع جملات آن که به سری مشهورند، اهمیت زیادی دارند. بسیاری از پدیده‌ها مانند تکثیر سلول‌ها، میزان افزایش اپیدمی و … از الگوهایی عددی مانند دنباله هندسی پیروی می‌کنند. در نتیجه شناخت چنین الگو یا دنباله‌هایی، امکان پیش بینی آینده چنین پدیده‌هایی را ممکن می‌سازد. البته در این متن با بررسی قدر نسبت دنباله هندسی می‌پردازیم که یکی از ارکان اصلی این تصاعد محسوب می‌شود. قصد داریم با ذکر چند مثال در این زمینه، با مفهوم قدر نسبت در دنباله هندسی بیشتر آشنا شده و آن را برای پیدا کردن جمله عمومی یا مقدارهای بعدی سری هندسی به کار گیریم.
در نوشتار دنباله هندسی و مجموع آن — به زبان ساده و سری همگرا و واگرا — از صفر تا صد با دنباله‌ها و شرط همگرایی آن‌ها آشنا شده‌اید. همچنین قواعد مربوط به سری توانی در مجله فرادرس به زبان ساده، شرح داده شده ولی در این متن قرار است دنباله هندسی را مورد بررسی قرار داده و قدر نسبت دنباله هندسی را شناسایی کنیم.
قدر نسبت دنباله هندسی
قبل از آنکه قدر نسبت دنباله هندسی را بشناسیم، بهتر است بدانیم دنباله چیست و به چه دنباله‌ای، هندسی می‌گویند. البته در ریاضی دنباله‌های متعددی وجود داشته که هر یک از آن‌ها کاربردهای خاص خود را برای نشان داده تغییرات پدیده‌ها دارند. دنباله‌ها در فیزیک و شیمی و بخصوص زیست‌شناسی به کار برده می‌شوند.
دنباله چیست ؟
یک «دنباله» (Sequence) یا تصاعد (Progression) به صورت یک ترتیب از اعداد نوشته و مشخص می‌شود. بین مقادیر و اعداد یک دنباله قانونی برقرار است که به کمک آن می‌توانیم با دانستن یک مقدار از دنباله، مقدار بعدی یا قبلی را مشخص کنیم. همین خصوصیات و ویژگی‌ها، باعث می‌شود که دنباله‌ها جذاب شده و بسیاری از محاسبات در ریاضیات را ساده‌تر کنند.
نکته: یک دنباله از اعداد به صورت مثلا $$1, 3, 5, 7, \ldots$$ نشان داده می‌شود. علامت $$\ldots$$ نشانگر نامتناهی بودن دنباله است. البته دنباله‌های متناهی نیز وجود دارند. مثال ۱ که در ادامه آمده است، یک دنباله متناهی را نشان می‌دهد. در حقیقت دنباله‌های متناهی، درست به مانند دنباله‌های نامتناهی هستند که در یک نقطه، قطع شده‌اند. در اغلب موارد، دنباله‌ها با بی‌نهایت جمله همراه هستند.
اگر هر جمله از یک دنباله را با مقادیر قبلی دنباله جمع کنیم، یک سری ساخته می‌شود. بنابراین «سری» (Series) از مجموع مقادیر دنباله‌ها پدید می‌آیند که این حاصل جمع‌ها در هر مقطع نیز ممکن است یک دنباله محسوب شوند.
مثال ۱: دنباله زیر را در نظر بگیرید. توجه داشته باشید که عبارت‌های این دنباله، دارای ترتیب است. به یاد دارید که مجموعه زیر یک الگوی هندسی از اعداد صحیح می‌گویند. زیرا هر یک از مقادیر آن، به صورت سه برابر مقدار قبلی است.
1, 3, 9, 27, 81, 243
این ترتیب را در الگوهای ریاضی نیز مورد بررسی قرار دادیم و در آنجا هم پیش‌بینی مقدار بعدی الگو، وابسته به ترتیب آن‌ها بود.
دنباله هندسی
در تعیین دنباله یا تصاعدها، رسم است که مقدار اول و قانون مربوط به تشکیل مقادیر بعدی را مشخص می‌کنند. به این ترتیب می‌توانیم دنباله را تکمیل کنیم. با توجه به این موضوع سعی می‌کنیم، قانون و شکل تصاعد یا دنباله اعداد مثال ۱ را مشخص کنیم.
$$ \large {\displaystyle 1, \overbrace{1 \times 3}^{3} ,\ \overbrace{1 \times 3 \times 3}^{ 9} ,\ \overbrace{ 1 \times 3 \times 3 \times 3}^{ 27},\ \overbrace{1 \times 3 \times 3 \times 3 \times 3}^{ 81}, \ \overbrace{1 \times 3 \times 3 \times 3 \times 3 \times 3 }^{ 243} }$$
با توجه به الگوی بالا، اگر هر جمله را بر جمله قبلی تقسیم کنیم، مقدار ثابتی بدست می‌آید که همان ۳ است. برای مثال جمله چهارم را بر جمله سوم تقسیم می‌کنیم.
$$ \large {\displaystyle 27 \div 9 = \dfrac{ 1 \times 3 \times 3 \times 3 }{ 1 \times 3 \times 3 } = 3} $$
توجه داشته باشید که این تقسیم فقط باید برحسب دو جمله پشت سر هم، انجام شود. این بار جمله ششم را بر جمله پنجم تقسیم می‌کنیم.
$$ \large {\displaystyle 243 \div 81 = 3} $$
نکته: این موضوع از قبل نیز مشخص بود. زیرا می‌دانستیم که هر جمله از ضرب عدد ۳ در جمله قبلی بدست می‌آید.
در مثال ۱، عدد ۳ که حاصل تقسیم دو عدد پشت سر هم در دنباله است، قدر نسبت دنباله هندسی می‌گویند و نقش مهمی برای تعیین دنباله هندسی دارد.
دنباله و تصاعدها در ریاضیات از اهمیت زیادی برخوردارند. این دنباله‌ها و همچنین سری، در فیزیک و شیمی و آمار به کار می‌آیند. در یکی از آموزش‌های فرادرس که برای مقطع دبیرستان تهیه شده، مبحث فیزیک پایه دهم به همراه مرور و حل تمرین آموزش داده شده است.
- برای مشاهده فیلم فیزیک – پایه دهم (مرور و حل تمرین) + اینجا کلیک کنید.
مثال ۲: دنباله اعداد زوج که یک دنباله نامتناهی از اعداد صحیح است را به صورت زیر در نظر می‌گیریم.
2, 4, 8, 16, 32, 64, 128, 256, …
مشخص است که با یک دنباله هندسی مواجه شده‌ایم، زیرا حاصل تقسیم هر دو عدد پشت سر هم از آن، مقدار ثابتی است.
$$ \large {\displaystyle \dfrac{ 4}{ 2} = \dfrac{ 8}{ 4} = \dfrac{ 16}{ 8} = \dfrac{ 32}{ 16} = 2 } $$
از آنجایی که این مقدار این نسبت‌ها، همگی برابر با ۲ هستند، ۲ را قدر نسبت دنباله هندسی اعداد زوج در نظر می‌گیریم.
مثال ۳: به کمک قدر نسبت و مقدار اولیه در تصاعد هندسی می‌توانیم دنباله را بسازیم. فرض کنید که قدر نسبت تصاعد هندسی برابر با ۵ باشد و مقدار اولیه تصاعد هم برابر با ۶ است. بنابراین می‌توانیم دنباله هندسی را به شکل ساده، محاسبه کرده و به صورت زیر بنویسیم.
$$ \large {\displaystyle 6 ,\ 6 \times 5, \ 6 \times 5 \times 5, \ 6 \times 5 \times 5 \times 5 , \ldots }$$
که نتیجه به صورت یک دنباله از اعداد در خواهد آمد که در ادامه قابل مشاهده‌اند.
6 , 30, 150, 750, 3750 , …
محاسبه قدر نسبت دنباله هندسی
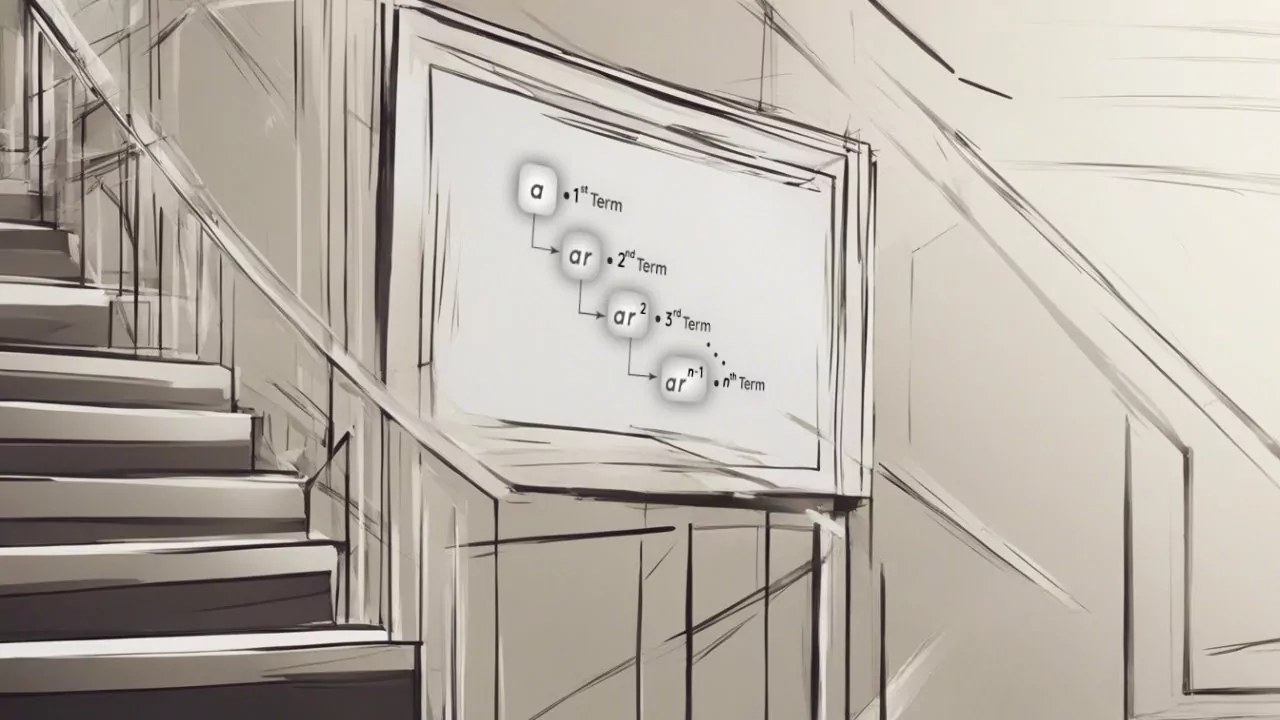
هدف این قسمت از متن، پیدا کردن رابطه بین مقادیر یک تصاعد یا دنباله هندسی است که به واسطه داشتن دو پارامتر اصلی این تصاعد، بتوانیم جمله‌های بعدی را مشخص کنیم. فرض کنید که بتوانیم در حالت کلی، تصاعد هندسی را با در نظر گرفتن جمله اول به صورت $$a$$ و مقدار قدر نسبت دنباله هندسی با حرف $$r$$، به شکل زیر بنویسیم.
$$ \large {\displaystyle a , \ a\ r, \ a\ r^2, \ a\ r^3, \ \ldots \quad \quad ; r \neq 0 }$$
به این ترتیب اگر $$x_n$$ را مقدار $$n$$ام یک دنباله هندسی در نظر بگیریم و $$a$$ همان مقدار اولیه باشد، پیدا کردن هر مقداری از دنباله هندسی مثل $$x_n$$ به صورت زیر خواهد بود. گاهی اوقات به $$n$$، اندیس جمله دنباله هندسی نیز می‌گویند. از آنجایی که اولین جمله تصاعد هندسی با $$x_1$$ مشخص می‌شود، باید شرط $$n \geq 1$$ در نظر گرفته شود.
$$ \large {\displaystyle x_n = a \ r^{(n -1)} , \; n \geq 1} $$
همچنین به کمک این قانون، رابطه زیر را بین تقسیم هر دو مقدار پشت سر هم این تصاعد کشف می‌کنیم.
$$ \large {\displaystyle x_{ n} \div x_{ n-1} = \dfrac{ x_n}{ x_{ n -1}} = r }$$
پس مقدار $$x_n$$ برحسب مقدار قبلی به صورت زیر درخواهد آمد.
$$ \large {\displaystyle x_{ n }= r \times x_{ n -1} }$$
حتی می‌توانیم مقدار قبلی را بر حسب مقدار بعدی مشخص کنیم. به رابطه زیر دقت کنید.
$$ \large {\displaystyle x_{ n – 1}= \dfrac{ x_n}{ r} } $$
البته در اینجا باید $$n >1$$ باشد. پس به این ترتیب قدر نسبت دنباله هندسی قابل محاسبه است. از طرفی باید قدر نسبت عددی غیر از صفر باشد. در غیر این صورت همه جمله‌ها، صفر خواهند شد. البته می‌توان قدر نسبت و جمله اول یک تصاعد هندسی را از بین اعداد حقیقی نیز انتخاب کرد. هر چند در مثال‌هایی که ارائه خواهیم کرد، از اعداد صحیح یا طبیعی کمک خواهیم گرفت.
قدر نسبت یا نسبت مشترک را در انگلیسی Common Ratio و جمله اول را هم با First Term می‌شناسیم. جمله عمومی تصاعد هندسی یا $$x_n$$ هم با عبارت General Term در انگلیسی شناخته می‌شود.
نکته: در یک تصاعد هندسی، باید قدر نسبت بین هر دو جمله متوالی یکسان و برابر باشد. به همین جهت به آن قدر نسبت مشترک (Common Ratio) نیز گفته می‌شود، زیرا در بین همه جمله‌ها، نسبت یا تقسیم هر جمله به جمله قبل ثابت و برابر است. در صورتی که در بعضی از جمله‌ها، چنین قانونی برقرار نباشد، تصاعد هندسی بوجود نخواهد آمد.
مثال ۴: مشخص کنید مقدار قدر نسبت دنباله هندسی زیر چقدر است؟
10, 30, 90, 270, 810, 2430, …
همانطور که گفتیم، باید خارج قسمت تقسیم هر دو جمله پشت سر، ثابت و یکسان باشد.
$$ \large {\displaystyle \dfrac{ 30} { 10} = \dfrac{ 270}{ 90} = 3 =r }$$
پس رابطه دنباله هندسی به صورت زیر درخواهد آمد. توجه داشته باشید که ذکر قدر نسبت و جمله اول در مشخص کردن دنباله هندسی ضروری است.
$$ \large {\displaystyle x_{ n} = 3 \times x_{ n -1} , \quad a = 10}$$
پس برای مثال، جمله هشتم این تصاعد، به شکل زیر محاسبه می‌شود.
$$ \large {\displaystyle x_8 = 10 \ r^{( 8 -1)} = 10 \times 3^7 = 21870 } $$
مثال ۵: برای دنباله زیر، مقدار قدر نسبت را محاسبه کنید و قانون تصاعد را مشخص نمایید.
4, 2, 1, 0.5, 0.25, …
جالب است که برعکس مثال‌های قبلی که دنباله هندسی، به صورت صعودی بود، این تصاعد به صورت نزولی است. به نظر می‌رسد که هر جمله از ضرب جمله قبلی در $$\frac{1}{2}$$ ساخته شده است، زیرا:
$$ \large {\displaystyle \dfrac{ 2}{ 4} = \dfrac{ 1}{ 2} = 0.5 = r} $$
بنابراین قدر نسبت را برابر با ۰٫۵ بدست آوردیم. به این ترتیب قانون این دنباله به صورت زیر نوشته می‌شود.
$$ \large {\displaystyle x_n = 0.5 \times \ x_{ n-1} } $$
همانطور که گفتیم، به کمک مقدار قدر نسبت و یکی از مقادیر، مقدار قبلی را محاسبه می‌کنیم.
$$ \large {\displaystyle x_2 = 2 = \dfrac{ 1}{ 0.5} = 2 } $$
همانطور که مشاهده کردید، زمانی که قدر نسبت بزرگتر از ۱ باشد، دنباله هندسی، صعودی است ولی در زمانی که قدر نسبت مقداری مثبت ولی کوچکتر از ۱ باشد، دنباله نزولی خواهد بود. اگر جمله هفتم این دنباله را احتیاج داشته باشیم، طبق رابطه عمومی دنباله هندسی، عمل خواهیم کرد. نتیجه به صورت زیر است.
$$ \large {\displaystyle x_n = 4 \times 0.5 ^{ n-1} } $$
$$ \large {\displaystyle x_7 = 4 \times 0.5 ^{ 7-1} = 4 \times 0.5^6 = 0.0625 } $$
نکته: به یاد داشته باشید که بحث مربوط به دنباله‌ها و مقادیر آن‌ها، مرتبط با اعداد صحیح یا طبیعی است. به همین علت قدر نسبت و همچنین مقادیر دنباله هندسی، همگی اعداد طبیعی هستند.
منفی بودن قدر نسبت دنباله هندسی
تا اینجا با دنباله‌های هندسی آشنا شدیم که مقادیر مثبت داشتند و در نتیجه قدر نسبت آن‌ها نیز مثبت بود. در این بخش با دنباله‌های هندسی آشنا خواهیم شد که قدر نسبت در آن‌ها منفی است.
مثال 6: به دنباله زیر توجه کنید و قدر نسبت و جمله عمومی آن را بیابید.
1, −3, 9, −27, 81, −243, …
از آنجایی که به صورت یک درمیان، جمله‌های تصاعدی هندسی منفی و مثبت است، متوجه می‌شویم که باید قدر نسبت، مقداری منفی باشد. ولی قاعده پیدا کردن قدر نسبت در اینجا، درست به مانند قبل است. کافی است دو جمله دنبال هم را بر هم تقسیم کنیم. اگر این نتیجه این تقسیم برای هر دو عبارت پشت‌سر هم، برابر باشد، قدر نسبت دنباله هندسی را پیدا کرده‌ایم.
$$ \large {\displaystyle \dfrac{ -3}{ 1} = \dfrac{ 9}{ -3} = \dfrac{ -27}{ 9} = -3 = r} $$
پس جمله عمومی این دنباله هندسی به صورت زیر نوشته می‌شود. واضح است که $$ a = 1$$ و $$ r = -3$$ خواهد بود.
$$ \large {\displaystyle x_n = 1 \times ( -3)^{( n -1)} } $$
پس برای مثال، جمله هفتم این دنباله به صورت زیر محاسبه می‌شود.
$$ \large {\displaystyle x_7 = 1 \times (- 3)^{( 7 -1)} = ( -3)^6 = 729 } $$
تذکر: می‌دانید که هر عدد منفی به توان زوج، یک عدد مثبت است. به همین جهت، تمامی جمله‌های با اندیس فرد این تصاعد هندسی، مثبت هستند و برعکس، تمامی جمله‌های با اندیس زوج نیز منفی خواهند بود.
مثال 7: برای دنباله زیر، قدر نسبت و جمله عمومی را پیدا کنید.
1, -0٫5, 0٫25, -0٫125, 0٫0625, …
مشخص است که با یک دنباله هندسی با قدر نسبت منفی مواجه هستیم. از طرفی اگر به قدر مطلق مقادیر این دنباله توجه کنیم، متوجه می‌شویم که قدر مطلق این مقادیر، نزولی هستند. طبق روش قبلی، قدر نسبت را محاسبه می‌کنیم.
$$ \large {\displaystyle \dfrac{ -0.5}{ 1} = \dfrac{ 0.25}{ -0.5} = \dfrac{ -0.125}{ 0.25} = -0.5 = r} $$
از آنجایی که خارج قسمت تقسیم هر دو جمله متوالی در این دنباله، برابر با ۰٫۵- است، پس قدر نسبت دنباله هندسی همان مقدار است. به این ترتیب جمله عمومی به صورت زیر بدست می‌آید.
$$ \large {\displaystyle x_n = 1 \times ( -0.5)^{( n-1)} } $$
پس اگر جمله ششم این دنباله را احتیاج داشته باشیم، کافی است مقدار $$n$$ را برابر با ۶ انتخاب کرده و محاسبات را طبق رابطه زیر اجرا کنیم.
$$ \large {\displaystyle x_6 = 1 \times (-0.5 )^{( 6 – 1)} = -( 0.5 )^5 = -0.03125 } $$
معرفی فیلم آموزش فیزیک – پایه دهم (مرور و حل تمرین)
لمس و شناخت پدیده‌های فیزیکی، احتیاج به تحقیق و بررسی زیاد دارد. در اغلب موارد دانش‌آموزان مقطع دبیرستان، وقتی با فیزیک آشنا می‌شوند، آن را جذاب و شوق‌انگیز می‌یابند و به کمک آن می‌توانند بسیاری از پدیده‌های طبیعی را توجیه و علت رخداد آن‌ها را مشخص کنند. در یکی از آموزش‌های فرادرس، که مخصوص مقطع دهم دبیرستان تهیه شده، حل مسائل و مرور مباحث فیزیک و ترمودینامیک مورد توجه قرار گرفته است. هدف از این آموزش، ارائه مختصری از درسنامه و در نهایت حل تمرین های مهم و کاربردی فیزیک دهم دبیرستان است. این آموزش شامل پنج درس است که با مباحث مربوط به اندازه‌گیری آغاز شده و موضوعات فیزیک مواد، شناوری، کار و انرژی، بایستگی و دما و گرما را شامل می‌شود. همچنین در انتهای این آموزش ترمودینامیک و قوانین اول دوم آن مورد بحث قرار گرفته است. در هر مبحث، مسائل و مثال‌های متنوعی ارائه می‌شود تا دانش‌آموزان را با روش حل مسئله‌ها آشنا کند.
زمان کلی برای این فیلم آموزشی ۱۴ ساعت و ۴۵ دقیقه است که با توجه به تنوع سوالات، به نظر کافی می‌رسد. از این آموزش برای حل مسائل کنکور نیز می‌توانید کمک بگیرید. آشنایی با ضرب و تقسیم اعداد صحیح از پیش‌نیازهای اولیه این بحث محسوب می‌شود.
- برای مشاهده فیلم فیزیک – پایه دهم (مرور و حل تمرین) + اینجا کلیک کنید.
خلاصه و جمع‌بندی
همانطور که خواندید، در ریاضیات و بحث دنباله‌ها، محاسبه و به دست آوردن قدر نسبت تصاعد یا دنباله‌های هندسی به ما کمک می‌کند که بتوانیم الگو های هندسی از اعداد را مشخص و تعیین کنیم. در این متن خواندید که قانون تشکیل تصاعد هندسی به دو پارامتر بستگی دارد. مقدار اولیه و قدر نسبت دنباله هندسی اجازه می‌دهند که بتوانیم مقدارهای دیگر دنباله را تشکیل داده و تصاعد را بشناسیم. مشخص شد که اگر قدر نسبت دنباله هندسی مقداری بزرگتر از ۱ باشد، دنباله صعودی است و اگر این مقدار، کوچکتر از ۱ و بزرگتر از ۰ باشد، دنباله را نزولی می‌نامیم.
