نمودار چیست؟ – انواع نمودار در ریاضی – تصویری و به زبان ساده
از نظر شما یک نمودار چیست ؟ آیا نمایشی از ستونها با ارتفاع مختلف است؟ یا دایرهای است که به قطاعهایی با اندازههای متفاوت تقسیم شده است. در همه این حالتها، دادهها را به شکل یک تصویر مشاهده میکنید. در حقیقت اگر بخواهیم به این سوال که نمودار چیست پاسخ دهیم، میتوانیم آن را یک شیوه برای نمایش اطلاعات و دادهها بدانیم. درک و سرعت دریافت اطلاعات از نمودارها نسبت به جدولها و گزارشهای متنی، بسیار بیشتر است. امکان مقایسه سریع، تشخیص روند و تغییرات در نمودارها به خوبی دیده میشود. حتی به کمک نمودارها میتوان رابطه بین متغیرها را هم شناخت. به همین جهت این نوشتار از مجله فرادرس را به پرسش نمودار چیست و پاسخ آن اختصاص دادهایم. ابتدا مفاهیم اولیه و ساده در سطح دبستان و دبیرستان برای رسم نمودارهای ستونی، دایرهای و خطی را شرح داده، سپس به نمودارهای مختلف در ریاضی و آمار میپردازیم.


برای آشنایی با انواع نمودارها و خصوصیات آنها توصیه میشود که نوشتارهای دیگر مجله فرادرس با عنوانهای رسم نمودار برای داده ها — معرفی و کاربردها (+) و رسم نمودار در ورد — به زبان ساده (+) را مطالعه کنید. همچنین خواندن مطالب کاربرد انواع نمودارها و گراف ها در اکسل (+) و رسم نمودار در متمتیکا — راهنمای سریع و کاربردی (+) نیز خالی از لطف نیست.
نمودار چیست ؟
نمودارها یک تکنیک گرافیکی برای نمایش یک مجموعه داده است. همین توصیف را برای انواع نمودارها میتوان به کار برد. اگر دادههایی از نوع کمی یا کیفی یا حتی ترکیبی داشته باشید، باز هم با رسم نمودارها میتوانید میزان آنها و حتی رابطه بین متغیرها را نمایش دهید.
نمودارها نمایش تصویری از رابطه بین متغیرها و مقدارهای آنها است. نمودارها برای نمایش اطلاعات بسیار مفید هستند و قادرند به سرعت، درک شده و اطلاعاتی را منتقل کنند که ممکن است از لیست یا جدولهای مقادیر، حاصل نشود. در اکثر موارد، با توجه به یک مقیاس یا خط کش، مقادیر در محورهای نمودارها، تقسیم بندی میشوند تا امکان مقایسه سادهتر شود .
برای مثال مقیاس یا مختصات نقاط در نمودارها یا مختصات دکارتی به صورتی است که برای متغیرهای کمی، روی هر دو محور یک مقیاس یا فاصلههای یکسان در نظر گرفته میشود. در نمودارهای لگاریتمی، محور عمودی به کمک لگاریتم متغیر وابسته (y) نمایش و ارائه میگردد.
برای خواندن و نمایش مقدار یک متغیر (تابع) برحسب یک متغیر دیگر، نمودارهای نقطهای یا خطی استفاده میشوند، اما این کار را همچنین با دادههای ارائه شده به صورت جدول نیز میتوان صورت داد. نمودارهای توابع در ریاضیات، علوم، مهندسی، فناوری، امور مالی و سایر زمینهها استفاده میشود.
نمودارهای آماری
همانطور که گفته شد، نمودارها میتوانند برای حل برخی معادلات ریاضی مورد استفاده قرار گیرند، برای مثال تعیین علامت و نمایش ریشههای معادلات و توابع در نمودارهای خطی یا رسم توابع امکانپذیر است.
از نظر شکل ظاهری و نحوه نمایش اطلاعات، نمودارها با یکدیگر تفاوت دارند. در بعضی از نمودارها امکان مقایسه بین مقادیر بوجود میآید در حالیکه بعضی دیگر مناسب برای نمایش روند تغییرات دادهها هستند. همچنین نمودارهایی وجود دارند که به نمایش رابطه بین متغیرها مربوط میشوند.
نمودارها به صورت دو بعدی یا سه بعدی ترسیم میشوند. مشخص است که در نمودارهای دو بعدی، دو متغیر به کار خواهد رفت ولی در نمودارهای سه بعدی، رابطه بین سه متغیر مشخص شده و به تصویر در میآید.
در بیشتر این موارد، اطلاعات و دادهها، در قالب یک جدول ارائه شده و برای نمایش تصویری آنها، نمودارها را به کار میگیریم. از آنجایی که درک نمودارها سادهتر است، اطلاعات مربوطه در زمان کمتری به مخاطب منتقل شده و درک آنها سادهتر هستند.
در ادامه به رسم سه نمودار، که به شکل خاص به کار میروند، میپردازیم. این نمودارها از اهمیت بیشتری در آمار برخوردارند و به کمک آنها، دادهها را بهتر میشناسیم.
نمودارهای ستونی
اگر بخواهیم دستههای مختلفی را با یکدیگر مقایسه کنیم، بهتر است نمودارهای ستونی را رسم کنیم. در این نمودارها دو محور عمود بر هم وجود دارد. محور افقی دسته یا گروهها را نشان میدهد و محور عمودی هم مربوط به مقادیر کمی است.
در اغلب موارد دسته یا گروهها را توسط یک متغیر کیفی نشان میدهیم. بنابراین در «نمودارهای ستونی» (Column Chart) محور افقی نشاندهنده مقدارهای متغیرهای کیفی است و محور عمودی یک کمیت (مثلا تعداد، درصد و یا میانگین) مربوط به هر یک از این گروهها را به نمایش در میآورد. به منظور روانی و خوانایی بیشتر در این نمودارها، خطوط تفکیکی روی نمودار، ظاهر شده که هم روی محور افقی و هم محور عمودی، بخشها و مقادیر را بهتر نشان دهد.
توجه داشته باشید که نمودارها براساس مقادیر عددی و جدول زیر ایجاد شده است. در ادامه یک جدول اطلاعاتی برای مقایسه تعداد جمعیت استانها دیده می شود.
جدول ۱: جمعیت استانها و مقایسه آنها
| نام استان | تعداد جمعیت |
| آذربایجان | 3,7۳۴,0۴0 |
| البرز | 2,5۳۲,0۱۲ |
| خراسان شمالی | 8,6۱۲,۴۳۴ |
| خراسان جنوبی | 6,50۴,0۶۶ |
| ایلام | 5,5۲0,۵۶۳ |
میخواهیم به کمک جدول بالا، نموداری ستونی رسم کنیم و به کمک آن بین استانها براساس تعداد جمعیت، مقایسه انجام دهیم.
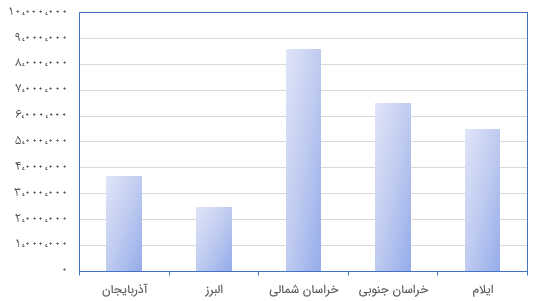
نکته: تشخیص اینکه بیشترین جمعیت مربوط به کدام یک از استانها است، کار مشکلی است. از طرفی تعیین کم جمعیتترین استان هم احتیاج به مقایسه بین مقدارها دارد. ولی رسم یک نمودار، این مقایسهها را سادهتر خواهد کرد و به سرعت، پرجمعیت و کم جمعیتترین استانها را پیدا خواهیم کرد.
برای رسم این نوع نمودار، مراحل یا گامهای زیر را طی خواهیم میکنیم.
- گام اول: روی محور افقی، چهار نیم خط کوچک برای مشخص کردن پنج ستون میکشیم. در وسط فاصله هر یک از نیمخطها هم نام یکی از استانها را مینویسیم.
- گام دوم: اعداد مربوط به جمعیت هر استان را در جدول ۱، برحسب میلیون نفر گرد میکنیم. با انجام این کار به جدول زیر خواهیم رسید.
جدول ۲: جمعیت گرد شده استانها
| نام استان | تعداد جمعیت (گرد شده برحسب میلیون) |
| آذربایجان | 3٫۷ |
| البرز | ۲٫۵ |
| خراسان شمالی | ۸٫۶ |
| خراسان جنوبی | ۶٫۵ |
| ایلام | ۵٫۵ |
- گام سوم: با توجه به اینکه اعداد را به میلیون گرد کردهایم، روی محور عمودی، تقسیمها را هم به میلیون تنظیم میکنیم. بنابراین اولین درجه روی این محور، نشان دهنده یک میلیون، دومین تقسیمبندی، ۲ میلیون و ... و آخرین هم ۹ میلیون بدست میآید. ولی برای اطمینان بیشتر و به دلخواه، تا مقیاس ۱۰ میلیون، تقسیمبندی را ادامه میدهیم.
- گام چهارم: روی محلهایی که روی محور افقی برای هر استان تعیین کردیم، به ارتفاع عدد مربوطه در جدول ۲، مستطیلی میکشیم که عرض آن مثلا ۱ سانت بوده و ارتفاع آن براساسا مقیاس محور عمودی، تنظیم میشود. برای مثال اگر مقدار جمعیت برای خراسان جنوبی برابر با ۶٫۵ است، فاصله بین ۶ میلیون و ۷ میلیون را نصف کرده و طول مستطیل را مشخص میکنیم. پس برای همه استانها، فاصله روی محور افقی را یکسان در نظر گرفته و عرض مستطیلها را یکسان میگیریم ولی طول آنها را با توجه به جدول ۲ مشخص میکنیم.
- گام پنجم: در صورتی که بخواهیم خوانایی برای نمودارها ایجاد کنیم، روی محورها و همچنین بالای نمودار، از اسامی خاص کمک میگیریم. برای مثال محور افقی را «نام استان» و محور عمودی را «جمعیت به میلیون نفر» نامگذاری کرده و برای نمودار هم نامی به شکل «مقایسه جمعیت استانها».
اکنون نموداری که میخواستید، آماده است. همانطور که در تصویر ۱ مشاهده میکنید، به راحتی روی نمودارتان میتوانید مستطیل با طول بزرگتر و کوچکتر را تشخیص دهید. پس پر جمعیتترین استان در این ۵ استان، خراسان شمالی و کم جمعیتترین نیز استان البرز است.
نکته: در نمودارهای ستونی، اولویت یا ترتیب مقادیر روی محور افقی به اختیار شما است و میتوانستید ابتدا استان خراسان شمالی را ترسیم کنید و در آخر هم استان البرز را قرار دهید. به بیان دیگر، ترتیب قرارگیری طبقه یا دستهها، مشخص نیست و هر کسی میتواند بنا به سلیقه و نظر خودش، ترتیب این مقدارها را تغییر دهد.
نمودارهای دایرهای
در استان خراسان جنوبی بررسی انجام شده و براساس میزان تولید زعفران، زرشک و عناب و صنایع دستی دادههایی طبق جدول ۳ ایجاد شده است. میخواهیم به وسیله نمودار دایرهای، یک مقایسه بین درصد فروش هر یک از این محصولات ارائه کنیم.
جدول ۳: میزان تولید محصول در استان خراسان جنوبی
| نام استان | میزان تولید (به تن) |
| زعفران | 3000 |
| زرشک | 4500 |
| عناب | 6300 |
| صنایع دستی | 10500 |
میخواهیم به کمک یک نمودار دایرهای، این مقادیر را یکدیگر مقایسه کنیم و سهم هر بخش از صنایع کشاورزی و روستایی را با یکدیگر مقایسه کنیم. همانطور که میدانید برای مقایسه سهم، از درصد کمک میگیریم. پس بهتر است گامهای زیر را طی کنیم.
- گام اول: تبدیل مقادیر به صورت درصد
- گام دوم: تبدیل مقادیر به صورت زاویه از یک دایره
- گام سوم: تقسیم قطاعهای دایرهای برحسب زاویهها و رنگآمیزی آنها
همین گامها را برای جدول 3 و رسم نمودار دایرهای برای صنایع روستایی و کشاورزی انجام خواهیم داد.
ابتدا این مقدارها (میزان تولید برحسب تن) را با استفاده از روش درصدگیری به صورت درصدی نشان دهیم. ابتدا باید جمع کل را بدست آوریم. سپس هر یک از مقدارهای مربوط به میزان تولید را به جمع کل تقسیم میکنیم و عدد اعشاری را به صورت درصدی نمایش میدهیم. جمع کل برابر است با 24300، پس با تقسیم هر یک از مقدارها بر این جمع کل، درصد یا سهم هر یک از بخشها بدست میآید. کافی است که عدد اعشاری بدست آمده را در ۱۰۰ ضرب کنیم و به شکل درصدی نمایش دهیم.
حاصل به صورت جدول زیر درخواهد آمد.
جدول ۴: میزان تولید محصول در استان خراسان جنوبی به درصد
| نام استان | میزان تولید (به درصد) |
| زعفران | ٪۱۲ |
| زرشک | ٪۱۹ |
| عناب | ٪۲۶ |
| صنایع دستی | ٪۴۳ |
واضح است که جمع این درصدها برابر با ۱۰۰ است. حال یک دایره را به ۱۰۰ قسمت تقسیم میکنیم. از آنجایی که هر دایره ۳۶۰ درجه است، هر قسمت از آن، یک زاویه ۳٫۶ درجهای محسوب میشود. به میزان این درجهها، روی دایره یک قطاع ترسیم میکنیم. برای مثال اگر درصد تولید برای زعفران ۱۲٪ است، ۱۲ تا ۳٫۶ که برابر با حدود ۴۴ درجه است، باید روی دایره مشخص شود. پس کافی است درصد را در ۳۶۰ درجه ضرب کنیم. این درجهها را در جدول ۵ مشاهده میکنید.
جدول ۵: میزان تولید محصول در استان خراسان جنوبی به صورت زاویهای از یک دایره (۳۶۰ درجهای)
| نام استان | زاویه روی دایره (درجه) |
| زعفران | 44 |
| زرشک | 67 |
| عناب | 93 |
| صنایع دستی | 15۶ |
طبق این الگو، قطاعهای دایره را رسم و رنگآمیزی میکنیم. تصویر زیر نموداری دایرهای برای دادههای جدول ۵ را نشان میدهد.
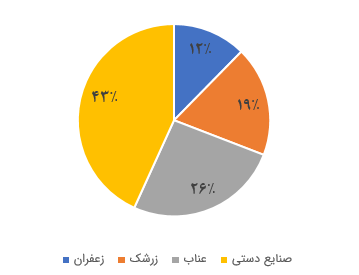
همانطور که مشخص است، سهم صنایع دستی از لحاظ وزن بیشتر از بقیه بخشها است و میتوان نتیجه گرفت که نیمی از تولید از لحاظ وزنی مربوط به صنایع دستی و نیمی دیگر مربوط به بخش کشاورزی است. پس با سرمایهگذاری روی بخش کشاورزی در استان خراسان جنوبی میتوان سهم بیشتری را به کشاورزی بخشید.
نمودارهای خطی
اگر اعدادی دارید که در طی زمان تغییر میکنند و میخواهید روند تغییرات آنها را رسم کنید، بهترین گزینه نمودارهای خطی هستند در نموداری که به شکل خطی رسم میشود، محور افقی زمان در نظر گرفته میشود که در طی آن، اندازه های مختلفی برای محور عمودی ثبت شده است. برای مثال فرض کنید که حداکثر دما هوا را در طول یک سال، در یک منطقه جغرافیایی مثلا شهر مشهد ثبت کردهایم.
جدول ۵: میزان تولید محصول در استان خراسان جنوبی به صورت زاویهای از یک دایره (۳۶۰ درجهای)
| ماه | حداکثر دما |
| فروردین | ۲۴ |
| اردیبهشت | ۲۷ |
| خرداد | ۳۳ |
| تیر | ۴۱ |
| مرداد | ۴۳ |
| شهریور | ۳۸ |
| مهر | ۲۶ |
| آبان | ۲۰ |
| آذر | ۱۲ |
| دی | ۸ |
| بهمن | ۷ |
| اسفند | ۱۸ |
روند تغییرات حداکثر دما در شهر مشهد را براساس یک نمودار خطی به صورت گامهای زیر ترسیم میکنیم:
گام اول: محور افقی را به ترتیب مقدارهای ستون اول جدول ۵ ایجاد میکنیم. بهتر است که فاصله بین این مقادیر روی محور یکسان باشد.
گام دوم: از محل قرارگیری هر ماه به میزان مشخص شده در ستون حداکثر دمای جدول ۵، یک نقطه را مشخص میکنیم. این نقطه نشانگر حداکثر دما در شهر مشهد در فصلهای مخلتف است که در محور افقی قرار گرفته.
گام سوم: نقاط بدست آمده از گام دوم را با یک خط به یکدیگر متصل میکنیم. این خطها در نقطههای ایجاد شده با یکدیگر برخورد میکنند و به این ترتیب به شکل نموداری پیوسته ولی شکسته درخواهند آمد. این کارها، نموداری خطی را برایتان مطابق با تصویر ۳ میسازد.
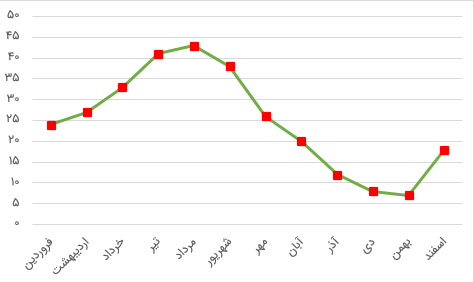
نکته: گاهی برای نمایش این خطوط، به جای خطوط شکسته شده، از خطهای منحنی استفاده میکنند که به این ترتیب منحنی مربوط به صورت هموارتر به نظر میرسد.
در این قسمت، به زبانی ساده به مفهوم نمودارها و نحوه رسم آن اشاره کردیم. ولی در بخش بعدی، با بیان علمی و تخصصی به نمودارها در ریاضی و آمار خواهیم پرداخت و کاربرد روشهای مصورسازی داده را مرور خواهیم کرد.
تا اینجا با انواع نمودارها آشنا شدیم. این نمودارها را میتوان با نرمافزارهای مختلفی مانند اکسل یا Grapher رسم کرد. با مراجعه به مجموعه آموزش رسم انواع نمودار فرادرس میتوانید با چگونگی رسم انواع نمودارها با استفاده از نرمافزارهای مختلف آشنا شوید.
انواع نمودارهای ریاضی و نقش و کاربرد آنها
نمودارها نقش مهمی در تجزیه و تحلیل دادهها و بخصوص آمار دارند. مطالعه داده و اطلاعات عددی به دو شکل در علم آمار و علم داده (Data Science) صورت میگیرد. در روش اول، شاخص یا مقادیر عددی (کمی) برای توضیح دادن ویژگیهای دادهها به کار میرود و در مقابل روشهای گرافیکی مانند نمودارها، به شکل تصویری این اطلاعات را به محقق و دانشمندان نشان میدهد.
در ادامه لیستی از روشهای کمی و شاخصهای آماری را مشاهده میکنید. هر یک از این موضوعات در مجله فرادرس شرح داده شدهاند. کافی است روی عنوانها کلیک کنید تا به صفحه مربوطه در مجله دسترسی پیدا کنید.
این تکنیکها و روشهای مشابه همگی ارزشمند هستند و از نظر تجزیه و تحلیل کلاسیک تکنیکهای اصلی محسوب میشوند. همچنین ابزارهای آماری بسیاری وجود دارد که به طور کلی از آنها به عنوان تکنیکهای گرافیکی یاد میشود. این موارد در ادامه لیست شدهاند.
- نمودارهای پراکندگی (Scatter Plot)
- نمودارهای طیفی (Spectrum plots)
- هیستوگرام (Histogram)
- نمودارهای احتمالی (Probability plots)
- نمودارهای باقیمانده (Residual plots)
- نمودارهای جعبهای (Box plot)
- طرح های بلوکی (Block Plot)
تکنیکها و روشهای گرافیکی مانند نمودارها، یک مسیر کوتاه برای به دست آوردن بینش از یک مجموعه داده از نظر بررسی آزمون فرض، انتخاب مدل مناسب، اعتبارسنجی مدل، انتخاب بهترین برآوردگر، شناسایی رابطه بین متغیرها، تعیین اثر فاکتور و تشخیص روند را شامل میشود. گرافیک آماری بینشی اساسی از جنبه ساختار اطلاعاتی را ارائه میدهند. در ادامه با چند نوع از این نمودارها و کاربردشان آشنا خواهیم شد.
نمودارهای دو طرفه (Biplot): این نوع نمودار، در آمار استفاده میشود. biplot یا نمودار دوطرفه، اجازه میدهد تا اطلاعات مربوط به دو نمونه و متغیرهای یک ماتریس داده به صورت گرافیکی نمایش داده شود. نمونهها به عنوان نقاط در نظر گرفته شده و در مقابل متغیرها به صورت بردار هستند. مقادیر با مسیر یک خط شکسته یا غیرخطی و منحنی نمایش داده میشوند. در مورد متغیرهای طبقهای، ممکن است از نقاط به عنوان سطوح یک متغیر دسته بندی استفاده شود. یک biplot تعمیم یافته اطلاعات مربوط به متغیرهای پیوسته و دسته ای را نمایش میدهد.
نمودارهای بلند-آلتمن (Bland – Altman): در شیمی تحلیلی و آمار زیستی این نمودارها روشی برای رسم داده است که در تجزیه و تحلیل همبستگی یا توافق بین دو رویکرد متفاوت بدست آمدهاند.
این طرح همان چیزی که در زمینههای دیگر علوم نیز به کار میرود اما توسط «بلاند» (Bland) و «آلتمن» (Altman) در آمار پزشکی مشهور شده است.
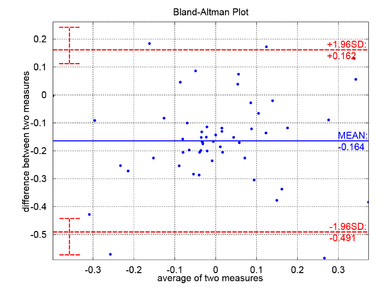
نمودارهای جعبه (Box Plot): در آمار توصیفی، نمودارهای جعبه که به عنوان نمودارهای «جعبه و خط» ( box-and-whisker) نیز شناخته میشود، روشی مناسب برای به تصویر کشیدن گرافیکی گروه دادههای عددی از طریق جمع بندی پنج شاخص است. کوچکترین مشاهده، چارک اول (Q1)، میانه (Q2)، چارک سوم (Q3) و بزرگترین مشاهده در این نمودارها نقش دارند. یک جعبه همچنین ممکن است مشخص کند کدام مشاهدات، دور افتاده هستند.
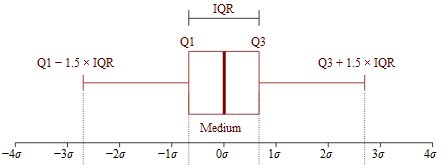
طرح فرش (Carpet Plot): طرح دو بعدی که تعامل بین دو و سه متغیر مستقل و یک تا سه متغیر وابسته را نشان میدهد، به نمودارهای طرح فرش معروف است. در تصویر زیر یک نمونه از نقشه طرح فرش را مشاهده میکنید که چهار متغیر را نشان میدهد. مربعهای مربوط به صفحه متغیرها، وجه تمایز این نوع نمودارها محسوب میشود.
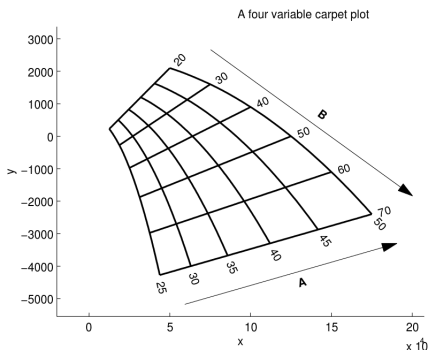
نمودارهای کانتور (Contour Plot): در این گراف، نمودارهای دو بعدی حضور دارند که منحنیهای مربوط به مقادیر یک متغیر را در خود نشان میدهند، این منحنیها، خطوط کانتور نامیده میشود که مقدار روی آنها ثابت است. در صورت تمایل، مقادیر رسم شده میتوانند کد رنگی داشته باشند.
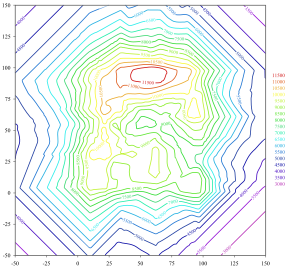
نمودارهای دالیتز (Dalitz Plot): این طرح به صورت نمودارهای پراکندگی (Scatter Plot) کشیده میشود و اغلب در فیزیک ذرات برای نشان دادن نوسان نسبی به کار میرود. در تصویر زیر که یک طرح Dalitz را نشان میدهد، موقعیت سه لبه یک ذره در حالت فروپاشی را مشاهده میکنید.
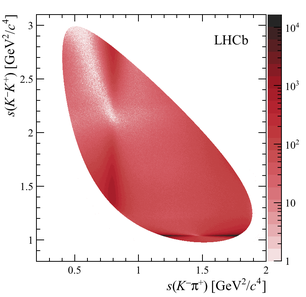
نمودارهای قیفی (Funnel Plot): این نمودار برای بررسی وجود سوگیری انتشار در متاآنالیز طراحی شده است. نمودارهای قیفی، که توسط «لایت» (Light) و «پیلمر» (Pillemer) در سال 1994 معرفی شد و به طور مفصل توسط «اگر» (Egger) و همکارانش مورد بحث قرار گرفت، نمودارهای قیفی ابزارهای مفیدی برای فراتحلیل هستند. طرح قیفی یک نمودار پراکندگی برای اثر تیمار در برابر اندازه یا حجم دادههای مورد مطالعه است. این نمودار، برای شناسایی اریبی و همگنی واریانسها به کار میرود.
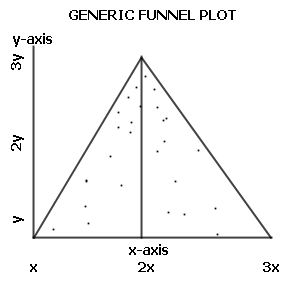
نمودارهای نقطه ای (Dot Plot): نمودارهای نقطهای یا «نمودارهای چارت نقطهای» (Dot chart)، نموداری آماری متشکل از گروهی از نقاط داده است که در یک مقیاس ساده یا مختصات دکارتی رسم شدهاند. نمودارهای نقطهای برای دادههای پیوسته، کمی و تک متغیره استفاده میشوند. اگر تعداد نقاط محدود باشند، ممکن است به جای نقطهها از برچسب دادهها در نمایش نمودار، بهره گرفته شود. نمودارهای نقطهای یکی از سادهترین نمودارهای موجود است و برای مجموعههای دادهای با اندازه کوچک تا متوسط مناسب است. از چنین نموداری برای برجسته کردن خوشهها و فاصله بین مقدارها کمک میگیرند. در زیر نمونهای از نمودار نقطهای را مشاهده میکنید.
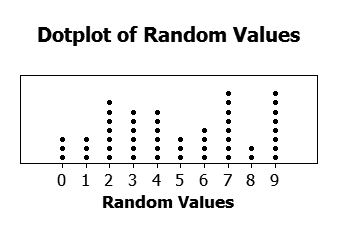
طرح جنگل (Forest Plot): این نمودار، یک نمایش گرافیکی است که قدرت شواهد در مطالعات علمی کمی را نشان میدهد. این نمودار، برای تحقیقات پزشکی به عنوان وسیلهای برای نمایش گرافیکی یک متاآنالیز از نتایج آزمایشات کنترل شده تصادفی ساخته شده است. در بیست سال گذشته، تکنیکهای مشابه فرا تحلیلی در مطالعات مشاهدهای (به عنوان مثال اپیدمیولوژی محیطی) اعمال شده است و از نمودارهای جنگل نیز اغلب در ارائه نتایج چنین مطالعاتی استفاده میشود.
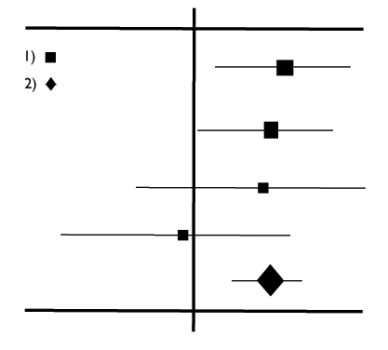
نمودارهای Galbraith: در آمار، طرح Galbraith که همچنین به عنوان نمودارهای شعاعی یا طرح شعاعی نیز شناخته میشود، یکی از روشهای نمایش چندین برآوردگر از پارامتر جامعه است که به همراه خطاهای استاندارد نمایش داده میشود. از طرفی این نمودار، میتواند برای بررسی ناهمگنی در یک متاآنالیز، به عنوان یک گزینه اصلی یا مکمل برای یک طرح جنگلی مورد استفاده قرار گیرد.
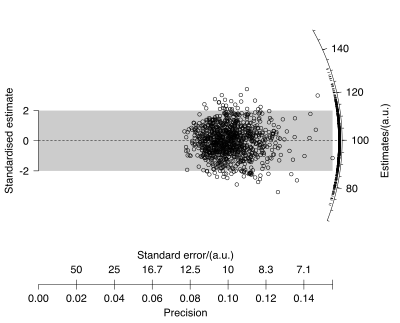
نقشه حرارت (Heat Map): نقشه حرارتی یا نمودارهای حرارتی، یک روش تجسم یا مصور سازی داده است که اندازه یک پدیده را به عنوان رنگ در دو بعد نشان میدهد. تنوع در رنگ ممکن است با توجه به رنگ و شدت متغیر باشد و نشانههای بصری (مثل نقطه یا خط) را در مورد چگونگی خوشهبندی یا تغییر پدیده به خواننده نشان میدهد. اساساً دو دسته از نقشههای حرارتی متفاوت وجود دارد. «نقشه گرمای خوشهای» (cluster heat map) و «نقشه حرارتی فضایی» (spatial heat map).
در یک نقشه گرمایی خوشهای، اندازهها به شکل ماتریسی از اندازه سلول که ردیفها و دستهها در ستونها قرار میگیرند، ساخته میشود. مرتب سازی ردیفها و ستونها اختیاری و به دلخواه کاربر صورت میگیرد. این نمودارها با هدف پیشنهاد یا نمایش خوشهها یا به تصویر کشیدن نقاط به صورت تجزیه و تحلیل یا روش اکتشاف آماری ساخته میشوند. اندازه سلول نیز دلخواه است اما باید به اندازه کافی بزرگ باشند که به وضوح قابل مشاهده شوند. در مقابل، موقعیت یک مقدار در یک نقشه حرارتی فضایی با قرار گرفتن مقدار در آن فضا باعث میشود تغییرات پیوسته در پدیده به تصویر درآیند. در زیر یک نمونه از نمودار نقشه حرارتی را مشاهده میکنید.
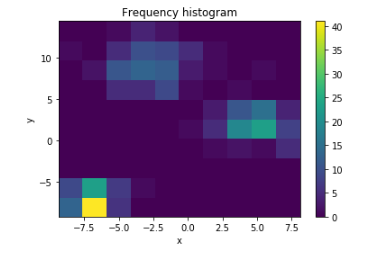
نمودارهای نیکولز (Nichols Plot): این گرافی است که در پردازش سیگنال مورد استفاده قرار میگیرد و در آن لگاریتم اندازه در برابر فاز پاسخ فرکانس در محورهای متعامد رسم میشود. در تصویر زیر یک نمونه از نمودار نیکولز را در ادامه متن مشاهده میکنید که برای تنظیم کنترلکننده مورد استفاده قرار گرفته است.

نمودارهای نیکویست (Nyquist Plot): از طرح در کنترل خودکار و پردازش سیگنال برای ارزیابی پایداری سیستم با بازخورد استفاده می شود. این یک از انواع نمودارها در مختصات قطبی است که در آن فاز یک پاسخ فرکانسی رسم میشود. در اینگونه نمودارها این مقادیر، فاز را به عنوان زاویه و اندازه را به عنوان فاصله از مبدا نشان میدهند.
در بیشتر موارد، در چنین نمودارهایی محور افقی که مقدار را نشان میدهد به مرحله پاسخ سیستم اشاره دارد. اگرچه دو نمودار Nyquist و Nichols یک کاربرد دارند ولی نمودار نیکولز در سیستم مختصات دکارتی ترسیم میشود در حالی که نمودار نیکویست، در سیستم مختصات قطبی کشیده خواهد شد.
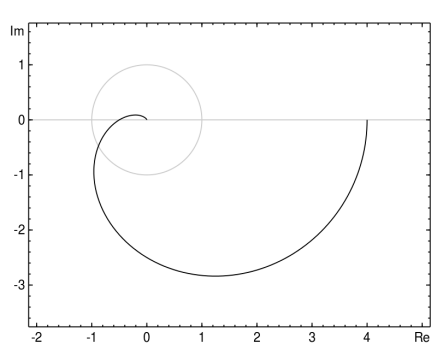
نمودارهای احتمال (Probability Plot): نمودار احتمال یا به شکل دقیق مقایسه احتمالی با توزیع نرمال، یک روش گرافیکی برای ارزیابی توزیع یا عدم توزیع تقریبی یک مجموعه داده با توزیع نرمال است. دادهها در برابر توزیع نرمال به شکل نظری به گونه ای رسم میشوند که نقاط باید یک خط مستقیم تقریبی را تشکیل دهند. دوری نقاط از این خط مستقیم، نشان دهنده خروج از توزیع نرمال است. البته این نمودارها را برای مقایسه توزیع دادهها با توزیعهای دیگر نیز میتوان استفاده کرد. به دلیل آنکه مقدار تابع چگالی یا احتمال در این نمودار مورد مقایسه قرار میگیرد، گاهی به آن p-p plot نیز میگویند.
در تصویر زیر یک نمونه از نمودارهای p-p plot را مشاهده میکنید که در محور افقی مقادیر تابع چگالی برای نقاط متناظر از توزیع نرمال و مقدار احتمال برای دادهها در محور عمودی دیده میشود. البته مشخص است که توزیع نرمال استاندارد و همچنین دادههای استاندارد شده در این نمودار، نقش ایفا میکنند. تناسب این نقاط با یک خط راست که از مبدا مختصات میگذرد و شبیه خط y=x است، نشانگر مطابقت دادهها با توزیع نرمال است. در تصویر زیر یک نمونه از نمودار p-p plot دیده میشود.
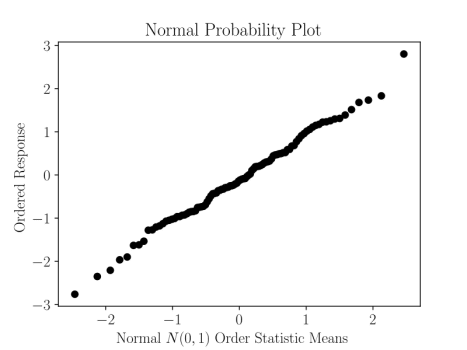
نمودارهای Q-Q: در آمار، نمودارهای Q-Q (Q مخفف چندک یا چارکها است) یک روش گرافیکی برای تشخیص تفاوت بین توزیع احتمال جمعیت آماری است که از آن نمونه تصادفی گرفته شده و توزیع مقایسهای است. این نمودار، نمونهای از بیان تفاوت بین توزیع دادهها با توزیع نرمال است که پارامترهای آن تعیین شده است. بنابراین نمودارهای Q-Q plot را روشی برای برازش توزیع نیز در نظر میگیرند.
نکته: روشهای دیگری نیز برای مطابقت با توزیع وجود دارد که براساس آماره بوده و به صورت نموداری ظاهر نمیشوند. برای مثال آزمون لامبدای ویلکس یا آزمون کولموگروف از این گونه هستند.
نمودارهای رگرسیون جزئی: در آمار کاربردی و مدلهای خطی، نمودارهای رگرسیون جزئی (Partial Regression plot) سعی دارد اثر افزودن متغیر دیگری به مدل را نشان دهد. با توجه به اینکه یک یا چند متغیر مستقل از قبل در مدل هستند باید مشخص کنیم که حضور متغیر جدید باعث بهبود مدل خواهد شد یا تاثیر چندانی در برازش خط رگرسیونی ندارد. از نمودارهای رگرسیون جزئی نیز به عنوان نمودارهای متغیر اضافه شده، نمودارهای متغیر تنظیم شده و نمودارهای ضریب جداگانه یاد میشود. نمودار رگرسیون جزئی توسط مولفههای زیر ترسیم و نمایش داده میشود. مشخص است که برای ترسیم این نمودارها سه گام باید طی شود.
- گام اول: محاسبه باقیمانده متغیر پاسخ از مقدار برازش شده در برابر متغیرهای مستقل اما با حذف متغیر .
- گام دوم: محاسبه باقیمانده های حاصل از رگرسیون در برابر باقیمانده متغیرهای مستقل دیگر.
- گام سوم: رسم باقیمانده از حاصل از گام اول در برابر باقیمانده از گام دوم.
رسم باقیمانده جزئی (Partial residual plot): در آمار کاربردی، نمودارهای باقیمانده یک تکنیک گرافیکی است که سعی دارد رابطه بین یک متغیر مستقل و متغیر پاسخ را نشان دهد. البته با توجه به برازش منحنی یا مدل رگرسیونی با همه متغیرها، فرض بر این است که متغیرهای دیگر نیز در مدل هستند و باقیماندهها براساس همه آنها محاسبه شدهاند.
نمودارهای پراکندگی (Scatterplot): نمودارهای پراکندگی یا نمودارهای نقطهای-پراکندگی نوعی نمایش دادهها است که با استفاده از متغیرها برای مجموعهای از دادهها مورد استفاده قرار میگیرد که قرار است پراکندگی و دوری یا نزدیکی مقادیر را نمایش دهد. این نمودارها توسط نقاطی در مختصات دکارتی دو بعدی یا سه بعدی نمایش داده میشود. هر یک از مقادیر یا ویژگیهای مربوط به نقطهها، روی یکی از محورها مشخص شده و موقعیت یا مختصات نقاط را تعیین میکنند.
در حالت دو بعدی از مختصات دکارتی استفاده شده و محور افقی، مولفه اول زوج مرتب مختصات و مولفه دوم نیز دومین مقدار از زوج مرتب را نشان میدهد. اغلب از این نمودارها برای نمایش رابطه بین دو نقطه یا رسم نمودارهای توابع در ریاضی نیز استفاده میشود. نمونهای از این نمودار را در تصویر زیر مشاهده میکنید.
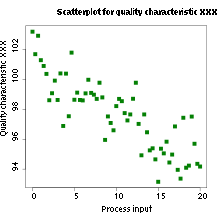
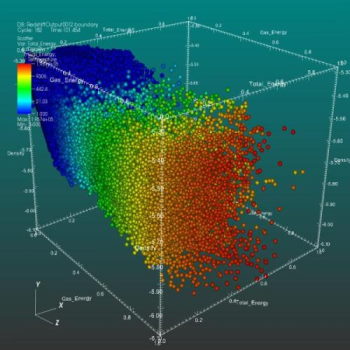
همچنین برای نمایش نقطههایی با سه مولفه، به یک نمودار پراکندگی به صورت سه بُعدی احتیاج دارید. نمونهای از نمودار پراکندگی سه بعدی را در تصویر زیر میبینید.
نمودارهای Shmoo: در مهندسی برق، طرح Shmoo نمایش گرافیکی پاسخ یک جز component یا سیستم است که در طیف وسیعی از شرایط و ورودیها متفاوت است. اغلب این نمودارها را برای نشان دادن نتایج آزمایش سیستمهای الکترونیکی پیچیده مانند رایانهها، پردازشگرهای ASIC یا ریزپردازندهها استفاده میکنند. این نمودارها معمولاً طیف وسیعی از شرایط کارکرد دستگاه را نمایش داده و نتایج آزمایش را نمایان میسازد.
نمودارهای اسپاگتی (Spaghetti plots): روشی برای مشاهده داده ها برای تجسم جریانات احتمالی از طریق سیستمها است. جریانهایی که به این روش نشان داده میشوند مانند رشته فرنگی به نظر میرسند، از این رو اصطلاحات اسپاگتی برای این نمودارها انتخاب شده است. این روش آمار برای اولین بار برای ردیابی مسیریابی در کارخانهها استفاده شد. تجسم جریان به این روش میتواند ناکارآمدی درون جریان سیستم را نشان داده و به کارشناسان در درک رفتار سیستم کمک کند.
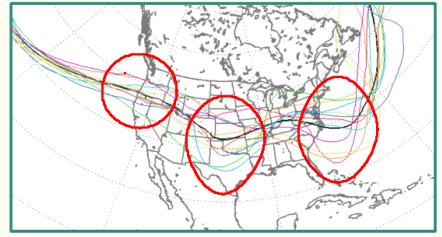
نمودارهای ساقه و برگ (Stemplot): طرح یا نمودارهای ساقه و برگ در آمار، برای نمایش دادههای هیستوگرام به صورت گرافیکی است که بوسیله آن امکان بازیابی اطلاعات از طریق نمودار نیز وجود دارد. نمودار ساقه و برگ، وسیلهای برای ارائه دادههای کمی در قالب گرافیکی، شبیه به هیستوگرام است و برای کمک به تجسم شکل توزیع آنها مناسب به نظر میرسد. این نمودارها بر اساس کارهای «آرتور بوولی» (Arthur Bowley) در اوایل دهه 1900 تکامل یافته و ابزارهای مفیدی در تحلیل دادههای اکتشافی محسوب میشود. بر خلاف هیستوگرامها، که در آن ستونها داده های اصلی را حداقل در تا دو رقم معنیدار نمایش میدهند، امکان به کارگیری روشهای آمار ناپارامتری را ندارد. در عوض نمودارهای ساقه و برگ این امکان را به محققین میدهد و اجازه بازتولید دادهها و قابلیت به کارگیری برای حالت کم بودن اطلاعات را هم ایفا میکند. در زیر یک نمودار ساقه و برگ را مشاهده میکنید. ساقهها نشانگر مقدار دهگان و برگها هم یکان را نشان میدهد.
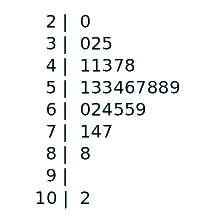
نمودارهای ستارهای (Star Plot): یک روش گرافیکی برای نمایش دادههای چند متغیره است. هر ستاره نماینده یک مشاهده است. به طور معمول، نمودارهای ستارهای در قالب چند طرح با تعداد زیادی ستاره در هر صفحه بوده و هر ستاره نشان دهنده یک مشاهده خواهد بود. گاهی به چنین نمودارهایی به خاطر شکل خاص آن، نمودار راداری هم گفته میشود.
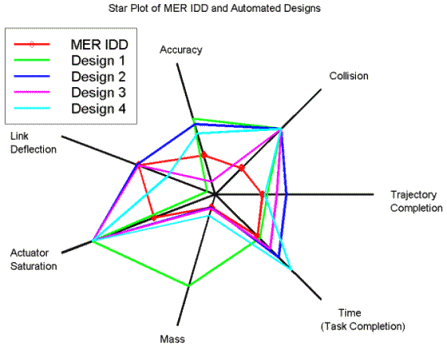
فقط توجه داشته باشید که در این نمودار، محورها دارای یک مقیاس باشند. در اغلب موارد این محورها نشانگر رتبه یا درصد هستند به این ترتیب، دارای هیچ واحد اندازهگیری نبوده و قابل مقایسه خواهند بود.
نمودارهای سطحی (Surface Plot): در این نوع نمودار، یک سطح ترسیم میشود تا متناسب با مجموعهای از سه تاییهای مرتب (X ، Y ، Z) باشد. این مختصات اگر به صورت یک تابع مثل Z با یکدیگر در رابطه باشند به صورت Z = f (X، Y) دیده خواهند شد. معمولاً مجموعه مقادیر X و Y روی محورها با یک مقیاس مشخص میشوند، از رنگها نیز میتوان برای مشخص کردن گروهها (متغیر دستهای یا کمی) استفاده کرد. پس چنین نمودارهایی را برای نمایش رابطه بین چهار متغیر کمی میتوان به کار گرفت.
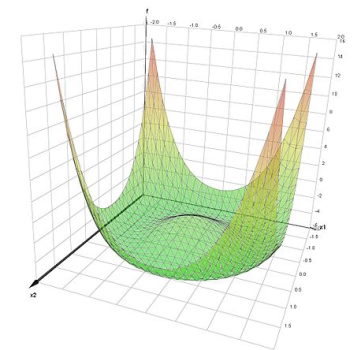
نمودارهای سه تایی (Ternary plot): نمودارهای سه تایی، نمودارهای مثلثی یا نمودارهای de Finetti نمودارهایی دو محوره برای نمایش همزمان مقدار سه متغیر است که به یک ثابت میرسند. این نوع نمودار، سه متغیر را به صورت موقعیت در یک مثلث متساوی الاضلاع به صورت گرافیکی نشان میدهد. از این نمودارها برای نشان دادن ترکیبات سیستمهای متشکل از سه گونه مقدار کمی (مثلا در پترولوژی ، کانی شناسی، متالورژی و سایر علوم فیزیکی) استفاده میشود. در ژنتیک جمعیت اغلب به آن نمودارهای «دی فینتی» (De Finetti) گفته می شود. همچنین در «تئوری بازی» (Game Theory)، اغلب به آن طرح ساده میگویند. در تصویر زیر یک نمونه از نمودار سه تایی یا مثلثی را مشاهده میکنید. محورها با یک مقیاس روی ضلعهای مثلث مشخص شدهاند.
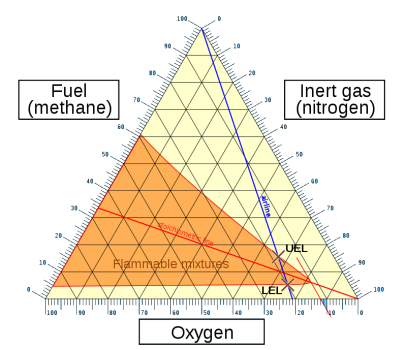
فیلد برداری (Vector Field): نمودارهای میدان برداری (یا نمودارهای لرزشی) جهت و قدرت بردار مرتبط با نقاط دو و سه بعدی را نشان میدهند. آنها معمولاً برای نشان دادن مشتقات روی یک سطح یا یک ناحیه به کار میروند.
نمودار طرح ویولن (Violin Plot): نمودارهای ویولنی روشی برای رسم دادههای عددی و کمی هستند.. آنها مشابه نمودارهای جعبهای بوده با این تفاوت که چگالی احتمال دادهها را در مقادیر مختلف نشان میدهند. در سادهترین حالت این نمودارها میتوانند شبیه یک هیستوگرام باشد. به طور معمول بدنه ویولن شامل یک نشانگر برای میانه دادهها و جعبه نشان دهنده دامنه بین چارکها است. از این جهت این نمودار بسیار شبیه به نمودارهای جعبه استاندارد خواهد بود.
ولی در نمودارهای ویولن مقدار خطای برآوردگرها روی این طرح جعبه قرار گرفته است. نمودارهای ویولن به کمک کتابخانهها یا بستههای نرم افزاری در برنامههای محاسبات آماری مانند زبان برنامهنویسی R یا پایتون در اختیار کاربران قرار گرفته است. البته نرم افزاهای دیگر مانند Stata از طریق افزودنی vioplot قادر به رسم چنین نمودارهایی خواهد بود. در تصویر زیر یک نمونه از نمودارهای ویولن قابل مشاهده است.
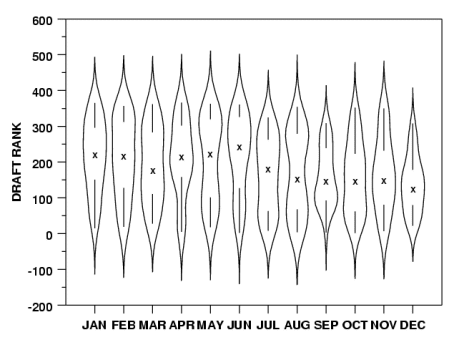
کاربرد نمودارها
انواع نمودارها و کاربردهای آنها بسیار متفاوت است. چند نمونه معمول کاربرد آنها در ادامه مورد توجه قرار گرفتهاند. ولی شما میتوانید بنا به نیازتان هر یک از نمودارها را برای نمایش بهتر دادهها، به کار بگیرید.
نمودارهای ساده: منحنیهای عرضه و تقاضا، نمودارهای سادهای که در اقتصاد برای ارتباط عرضه و تقاضا با قیمت استفاده میشوند در این گروه قرار میگیرند. از نمودارها ساده، میتوان برای تعیین تعادل اقتصادی (در اصل برای حل یک معادله) هم استفاده کرد. نمودار سادهای که برای خواندن مقادیر مورد استفاده قرار میگیرند مانند نمودار تابع چگالی احتمال چه برای توزیع نرمال یا گاوسی یا توزیعهای دیگر در این گروه هستند.
نکته: به یاد دارید که نمودار تابع چگالی توزیع احتمال نرمال یا گاوسی به شکل زنگ است. برای مثال به کمک چنین نموداری، میتوان احتمال اینکه مردی دارای قدی در یک بازه عددی باشد را محاسبه کرد. فرض بر این است که توزیع قد مردان بالغ را توزیع نرمال در نظر گرفته و با مشخص کردن میانگین و واریانس قد این افراد، پارامترهای جامعه آماری را مشخص کردهایم.
نمودارهای پیچیده: نمودار روان سنجی، نمودارهایی مربوط به تغییرات دما، فشار، رطوبت و سایر مقادیر در این گروه قرار دارند.
نمودار با مختصات غیر مستطیل: موارد فوق از مختصات مستطیل دو بعدی استفاده میکنند. یک مثال از نمودار با استفاده از مختصات قطبی که گاهی اوقات به صورت سه بعدی است، نمودار الگوی تابش آنتن است که نشان دهنده توان تابش شده از هر جهت به یک آنتن از نوع مشخص است. این نمودارها در درسها و مطالعات مخابرات به وفور به کار گرفته میشوند.
خلاصه و جمعبندی
در این نوشتار به این پرسش پاسخ دادیم که نمودار چیست و انواع آن را در حوزه داده و همینطور ریاضی مشخص کردیم. همانطور که خواندید برای نمایش تصویری دادهها از نمودار استفاده میشود. شکل ظاهری نمودار می تواند در نحوه انتقال اطلاعاتی که در دل دادهها و اعداد قرار گرفته، تاثیرگذار باشد. هر نوع نمودار برای شناسایی یا مشخص کردن یک یا چند خاصیت دادهها به کار میرود. به همین علت ممکن است برای یک مجموعه داده، چندین نمودار ترسیم شود تا رفتار آنها به خوبی درک شود.












