نمودارهای پراکندگی

نمودار پراکندگی جز آن دسته از نمودارهایی است که به طور معمول در ابتدای امر بررسی دادهها از آن استفاده میشود. پراکندگی دادهها، توزیع دادهها و محدوده آنها را می توان بر اساس نمودارهای پراکندی مشاهده کرد. نمودار پراکندگی جهت مشاهده جزئیات دادهها نیست؛ بلکه کلیتی از روابط بین دادهها را به نمایش میگذارد. به وسیله نمودار پراکندگی می توان رابطه بین دو متغیر عددی را بررسی کرد. برای مقال در واحد پشتیبانی یک شرکت رابطه تعداد تماسها و تعداد سفارشها با استفاده از نمودار پراکندگی قابل بررسی است. نمودار پراکندگی (XY)، نقطه هایی روی خود دارد که ارتباط بین دو نوع از داده ها را نمایش می دهند.
مثال: رابطه قد و وزن
در تصویر مثال زیر هر نقطه، وزن یک شخص را در مقایسه با قد او نشان می دهد.
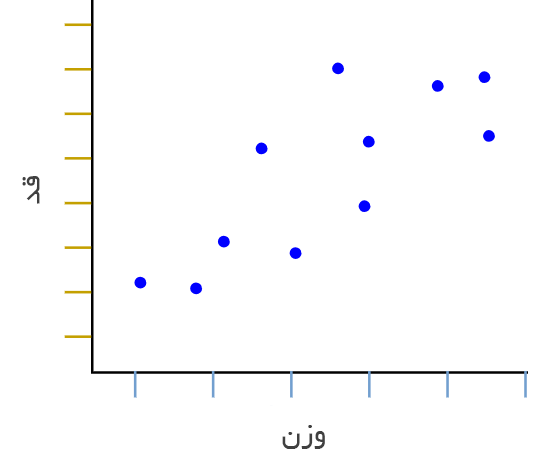
در ادامه یک مثال دیگر را بررسی میکنیم. فرض کنید بستنی فروشی محله به دنبال این است که بفهمد تعداد بستنیهایی که در یک روز میفروشد چه رابطهای با دمای ظهر آن روز دارد. نتایج به دست آمده برای 12 روز به شکل زیر است:
| فروش بستنی بر اساس دمای ظهر | |
| دما °C | فروش بستنی |
|---|---|
| 14.2° | 215 هزار تومان |
| 16.4° | 325 هزار تومان |
| 11.9° | 185 هزار تومان |
| 15.2° | 332 هزار تومان |
| 18.5° | 406 هزار تومان |
| 22.1° | 522 هزار تومان |
| 19.4° | 412 هزار تومان |
| 25.1° | 614 هزار تومان |
| 23.4° | 544 هزار تومان |
| 18.1° | 421 هزار تومان |
| 22.6° | 445 هزار تومان |
| 17.2° | 408 هزار تومان |
در ادامه همان دادهها این بار در نمودار پراکندگی رسم شدهاند:
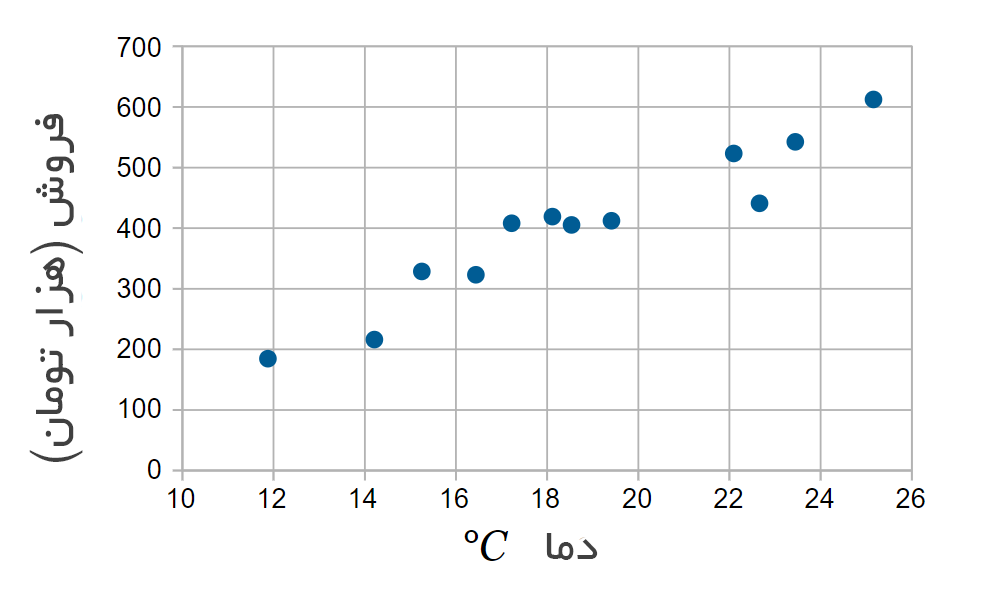
اکنون به راحتی میتوان فهمید که هوای گرم باعث فروش بیشتر میشود؛ اما این نسبت کاملاً صحیح نیست.
خط روند
ما همچنین می توانیم «خط روند» یعنی (Trendline) یا (Line of Best Fit) را روی نمودار پراکندگی رسم کنیم.
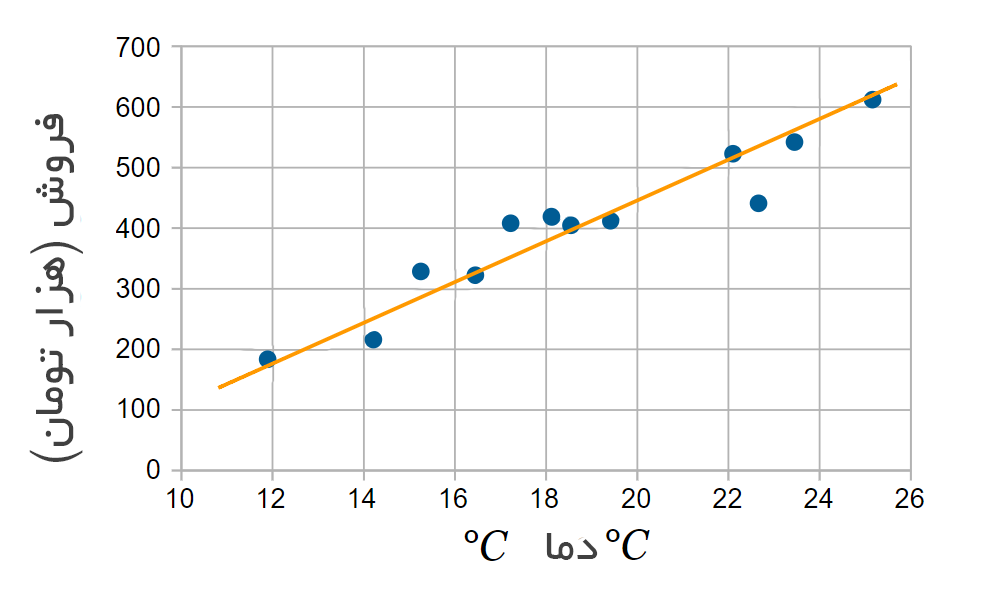
سعی بر آن است که خط را طوری رسم کنیم که تا حد ممکن به تمامی نقاط نزدیک باشد، و نقاط بالای خط تقریبا برابر با نقاط زیر آن شود.
مثال: بالا آمدن سطح آب دریا
نمودار پراکندگی برای بالا آمدن سطح دریا چنین است:
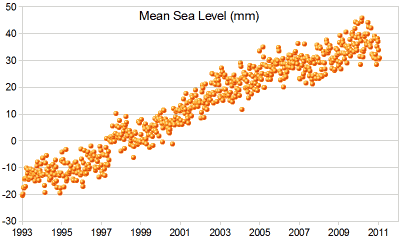
ما «خط روند» را برای آن به صورت زیر رسم میکنیم:
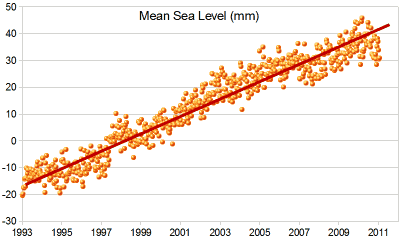
درونیابی و برونیابی
«درونیابی» (Interpolation) به عملی گفته میشود که طی آن یک مقدار را داخل نقاط دادهها پیدا میکنیم.
در اینجا ما از درونیابی خطی برای تخمین میزان فروش در دمای 21 درجه سانتیگراد کمک میگیریم.
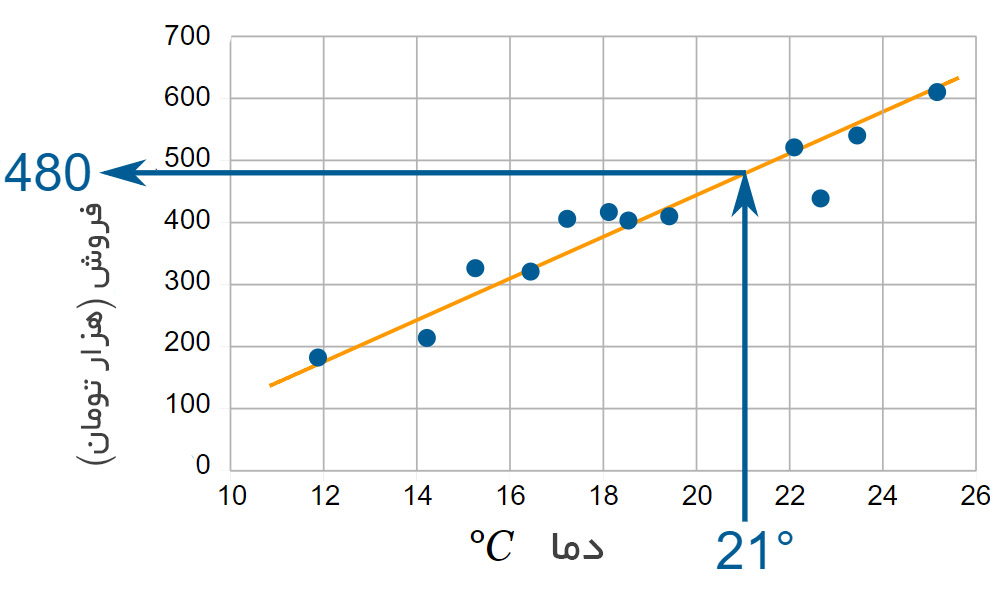
«برونیابی» (Extrapolation) به عملی گفته میشود که طی آن یک مقدار را خارج از نقاط دادهها پیدا میکنیم. در اینجا ما از برونیابی خطی برای تخمین میزان فروش در دمای 29 درجه سانتیگراد (که از تمامی دادههای ما بزرگتر است) کمک میگیریم.
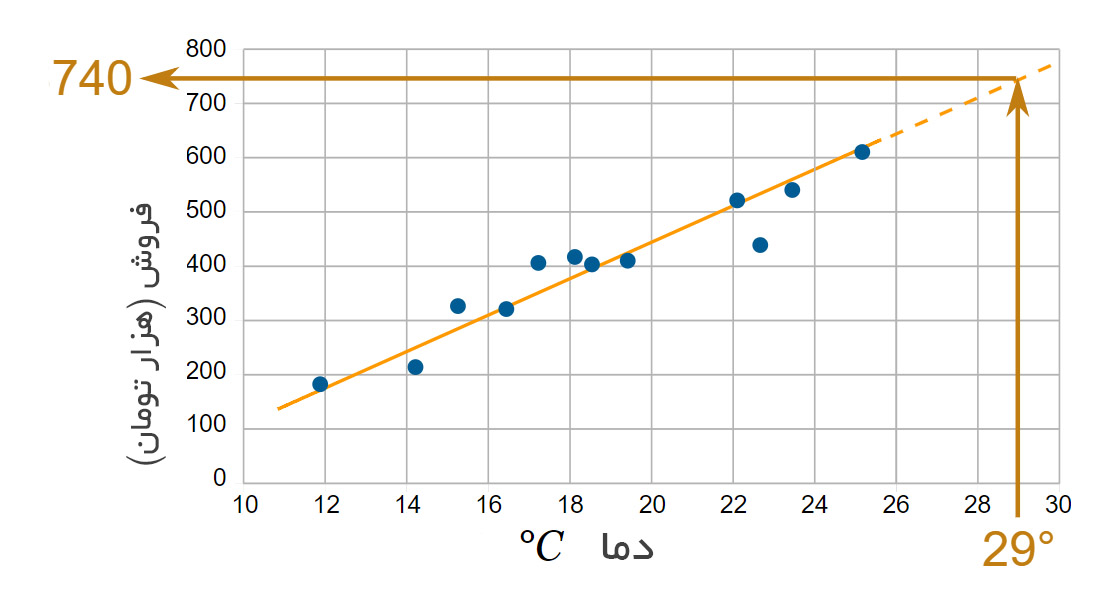
مثال:
ما می توانیم یک «معادله خط از دو نقطه» را به کمک نمودار بالا به دست آوریم. اکنون دو نقطه روی خط به صورت (180 هزار تومان و °12) و (610 هزار تومان و °25) در نظر می گیریم که به مقدار واقعی نزدیک باشد. ابتدا شیب را پیدا میکنیم:
تغییرات x ÷ تغییرات y = شیب m
= (610 − 180) ÷ (25° − 12°)
= 430 ÷ 13°
= 33 (گردشده)
اکنون مقدار شیب و همچنین مختصات نقطه (180 هزار تومان و °12) را در فرمول «شیب - خط» قرار می دهیم:
y − y1 = m(x − x1)
y − 180 = 33(x − 12)
y = 33(x −12) +180
y = 33x − 396 + 180
y = 33x − 216
اکنون از این معادله میتوان برای درونیابی میزان فروش در دمای 21 درجه سانتیگراد استفاده کرد:
y = 33 × 21 − 216 = 477
و برای برونیابی میزان فروش در دمای 29 درجه سانتیگراد:
y = 33 × 29 − 216 = 741
مقادیر به دست آمده به مقادیر روی نمودار نزدیک هستند؛ اما این به این معنی نیست که آنها دقت بیشتری (یا کمتری) دارند. این ها فقط اعداد تخمینی هستند.
نکته: از برونیابی نباید در مورد نقاط دوردست استفاده شود. برای مصال چه مقدار فروشی را در دمای °0 میتوان فرض کرد؟
y = 33 × 0 − 216 = −216
منفی 216 هزار تومان نشان میدهد که بسیار دور رفتهایم. دقت کنید که ما از درونیابی و برونیابی خطی (روی خط) استفاده کردیم؛ اما انواع دیگری نیز وجود دارند، برای مثال می توانیم از چند جملهایها برای ساختن خطوط منحنی استفاده کنیم.
همبستگی
هنگامی که دو دسته از دادهها شدیداً به هم مرتبط و وابسته باشند، میگوییم که آنها همبستگی بالایی دارند.
«کلمهی همبستگی از ترکیب هم (به معنی باهم) و وابستگی تشکیل شده است»
- همبستگی زمانی مثبت است که مقادیر نسبت به هم افزایش یابند.
- همبستگی زمانی منفی است که یک دسته از دادهها با افزایش دسته دیگر، کاهش یایند.
مانند نمودارهای زیر:
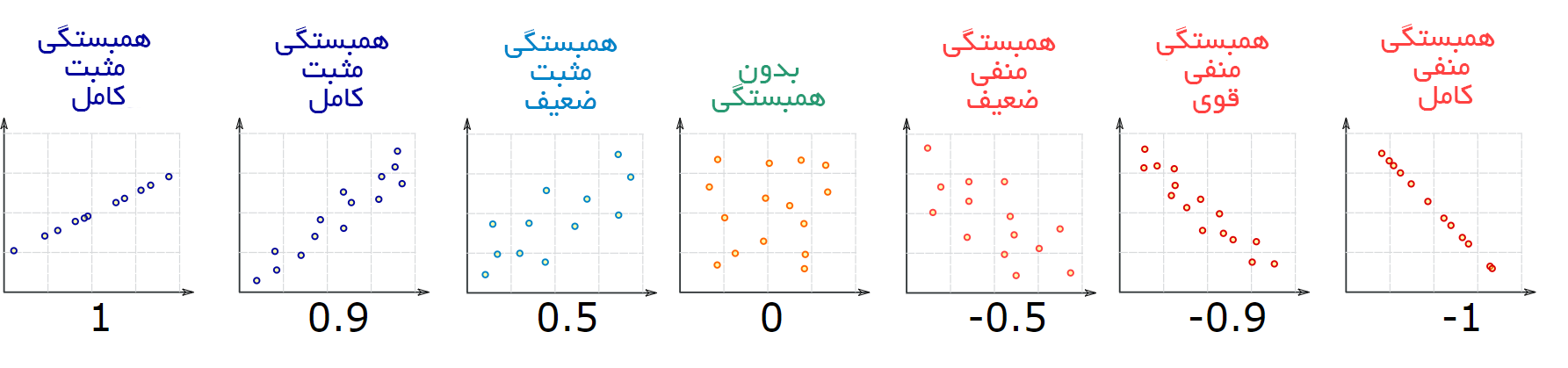
همبستگی منفی
همبستگی میتواند منفی باشد، به این معنی که رابطهای بین دو دسته داده وجود دارد؛ اما با افزایش یک دسته، دسته دیگر کاهش می یابد. مثالی از همبستگی منفی بین میزان زاد و ولد با نسبت به درآمد است، یعنی میزان زاد و ولد ظاهراً در کشور های پر درآمد کمتر است:
| کشور | تولید سالانه سرانه | نرخ تولد |
| ماداگاسکار | $800 | 5.70 |
| هند | $3,100 | 2.85 |
| مکزیک | $9,600 | 2.49 |
| تایوان | $25,300 | 1.57 |
| نروژ | $40,000 | 1.78 |
در زیر، نمودار پراکندگی برای تقریبا 100 کشور آمده است.
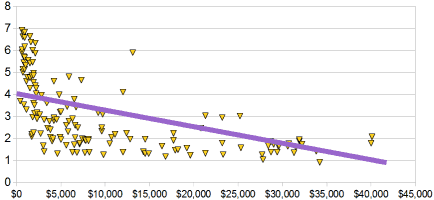
این نمودار، همبستگی منفی دارد، چون شیب خط به سمت پایین است. دقت کنید که در اینجا تلاش کردیم یک خط راست را روی نمودار رسم کنیم؛ اما شاید یک منحنی بهتر باشد. نظر شما چیست؟
اگر این نوشته برای شما مفید بوده است، آموزشهای زیر به شما پیشنهاد میشوند:
- مجموعه آموزشهای نرمافزارهای آماری
- رگرسیون خطی — مفهوم و محاسبات به زبان ساده
- مجموعه آموزشهای آمار، احتمالات و دادهکاوی
- نمودارهای میلهای – ستونی – به زبان ساده
- مفاهیم آماری – شاخصهای توصیفی
==












توضیحات کامل و واضح و عالی بود,با تشکر از شما.
سپاسگزارم، بسیار عالی بود…