نیکویی برازش توزیع در SPSS – راهنمای کاربردی

همانطور که در دیگر نوشتارهای فرادرس در حوزه آمار و تحلیل داده‌های آماری خوانده‌اید، می‌دانید تشخیص و به کارگیری توزیع احتمالی برای مشاهدات یا نمونه‌ها، از اهمیت زیادی برخوردار است. به همین دلیل آزمون‌هایی به نام «نیکویی برازش توزیع» (Goodness of Fit test) ایجاد شده تا قبل از اجرای تحلیل‌های آماری، از توزیع احتمالاتی داده‌ها با خبر شویم. این گونه آزمون‌ها از آنجایی که بدون در نظر گرفتن توزیع، محاسبات را انجام می‌دهند، متعلق به روش‌ها و آزمون‌های ناپارامتری هستند.

در این نوشتار با استفاده از دستورات نرم‌افزار SPSS نحوه اجرای این گونه آزمون‌ها را مرور خواهیم کرد. از آنجایی که این کار بوسیله روش‌های آزمون فرض آماری و براساس آماره‌ای با توزیع کای ۲ صورت می‌گیرد خواندن مطلب آزمون‌ نیکویی برازش (Goodness of Fit Test) و استقلال — کاربرد توزیع کای2 و آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات برای آگاهی از اصطلاحات و مفاهیم اولیه پیشنهاد می‌شود. همچنین مطالعه نوشتار مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری نیز خالی از لطف نیست.

نیکویی برازش توزیع

فرض کنید مشاهداتی از تعداد فروش چند نوع گوشی همراه در اختیار شما قرار گرفته است. اطلاعات مربوط به این داده‌ها با قالب فشرده از اینجا قابل دریافت است. ابتدا فایل را دریافت کرده و از حالت فشرده خارج کنید.

پس از فراخوانی این اطلاعات در SPSS صفحه‌ای مانند تصویری که در ادامه مشاهده می‌کنید، ظاهر می‌شود. در ستون اول کد دستگاه (id) و در ستون دوم نیز مدل دستگاه (brand) قرار گرفته است.

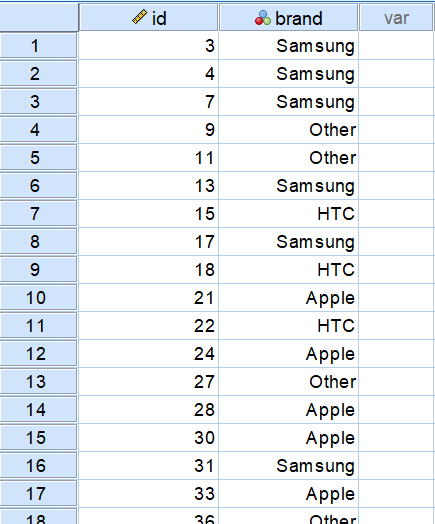
هدف از انجام آزمون در این مثال، مشخص کردن هم توزیعی برای نوع گوشی‌ها است. اگر خریداران به نوع گوشی خریداری شده اهمیت ندهند انتظار داریم که تعداد یا درصد گوشی‌های فروخته شده به صورت یکسان بین کل فروش‌ها، تقسیم شده باشد. چنین آزمونی را از نوع آزمون نیکویی برازش یا هم‌توزیعی در نظر می‌گیرند. در نوشتار آزمون‌ نیکویی برازش (Goodness of Fit Test) و استقلال — کاربرد توزیع کای2، مفاهیم اولیه این آزمون به طور کامل توضیح داده شده است. در اینجا قصد داریم محاسبات مربوط به این آزمون را در SPSS‌ اجرا کنیم.

با توجه به شیوه اجرای آزمون، در اینجا فرض صفر هم‌توزیع احتمالی این گوشی‌ها یا برابری درصدهای (توزیع احتمالی) گوشی‌ها در نظر گرفته شده است. درنتیجه خواهیم داشت:

$$\large \begin{cases}H_0: & p_1=p_2=\cdots =p_k\\ \large H_1: & \text{There are some different p's. }\end{cases}$$

واضح است که شرایط زیر برای $$p_i$$ها که درصد یا همان احتمال رخداد هر یک از پیشامدها است، باید برقرار باشد.

$$\large 0 < p_i < 1,\;\;\;\;\;p_1+p_2+\cdots+p_k=1$$

بنظر می‌رسد قبل از اجرای آزمون بهتر باشد جدول و نموداری از وضعیت تعداد (فراوانی) یا احتمال (درصد) فروش‌ها ترسیم کنیم. این کار را به وسیله دستور Frequency از فهرست Data Analysis و گزینه Descriptive Statistics انجام می‌دهیم.

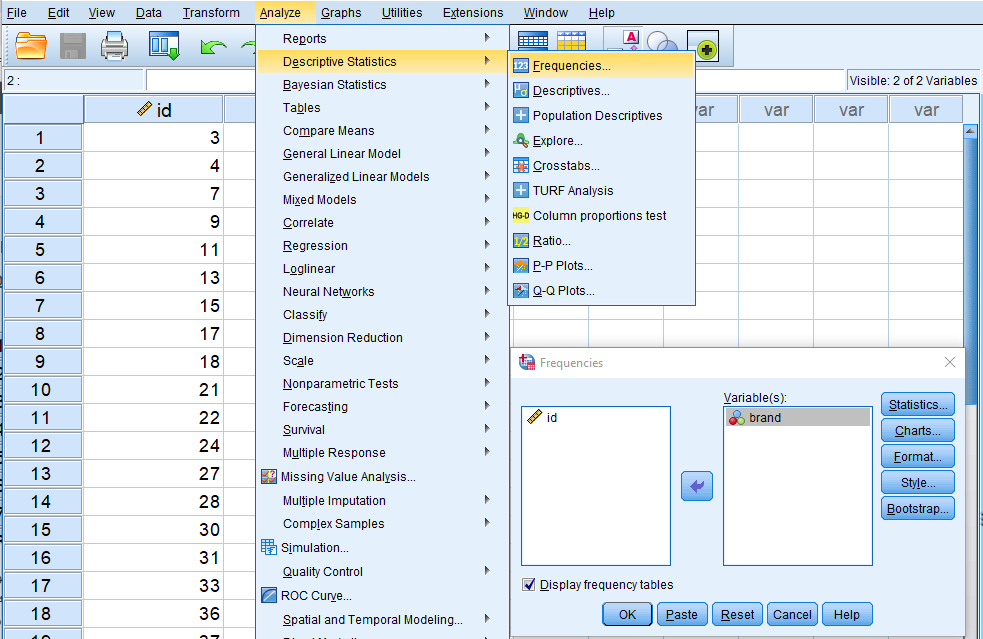
با تنظیمات پارامترهای این دستور مطابق تصویر بالا و فشردن دکمه ...Charts به پنجره انتخاب نوع نمودار وارد می‌شوید. کافی است گزینه Bar Charts را انتخاب کرده، تا نمودار ستونی به همراه جدول فراوانی ترسیم شود.

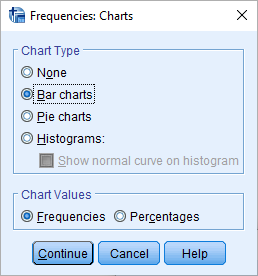
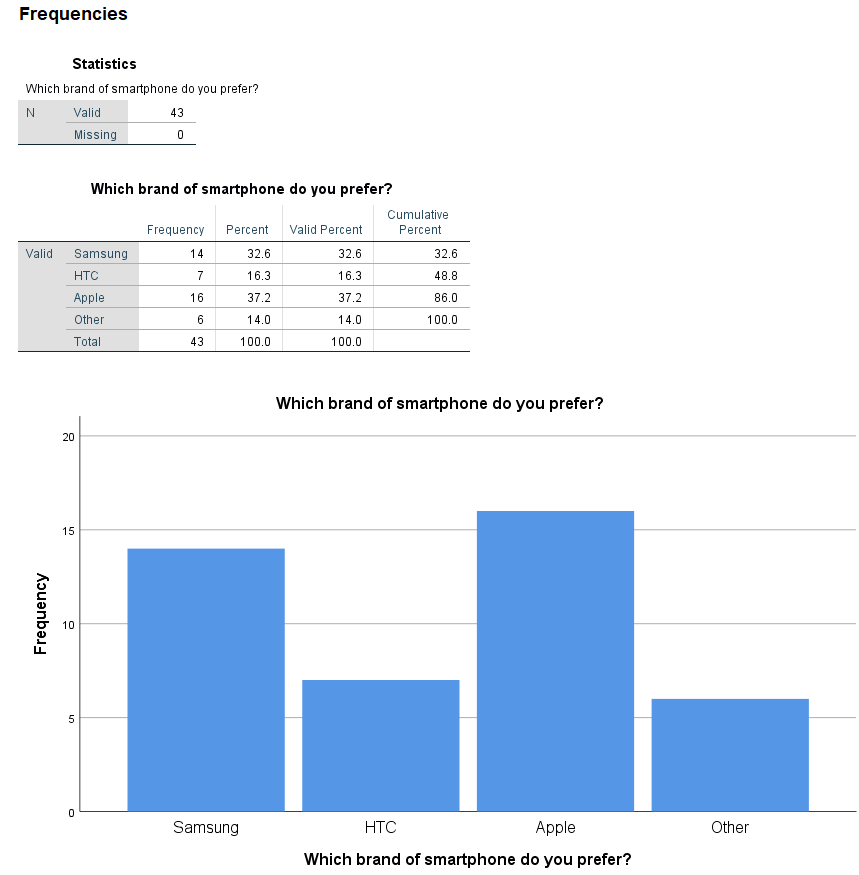
برای بازگشت به پنجره قبلی از دکمه Continue‌ استفاده کرده و پس از بازگشت از پنجره اصلی دکمه OK را انتخاب کنید تا خروجی به شکل زیر حاصل شود. مطابق تصویر زیر به نظر می‌رسد که فراوانی مربوط به هر یک از انواع گوشی با یکدیگر مطابقت نداشته و یکسان نیستند.

نکته: از آنجا که اطلاعات در ستون brand به صورت عددی وارد ولی برای هر عدد برچسب متنی در نظر گرفته شده است، با رسم نمودار Histogram مقدارهای عددی در محور افقی قرار می‌گیرند. برای رفع این مشکل از نمودار Bar Charts استفاده کرده‌ایم تا برچسب مقدارها که به صورت نام برند یا نام تجاری گوشی است، روی محور افقی دیده شود.

به منظور استفاده از ذخیره‌سازی دستورات نیز می‌توانید کد زیر را در پنجره کدنویسی Syntax در SPSS وارد و اجرا کنید. البته این کد را با استفاده از دکمه Paste از پنجره دستور نیز می‌توانید درج کنید.

مطابق با آنچه در جدول فراوانی دیده می‌شود،‌ به نظر می‌رسد درصد مربوط به فروش هر یک از انواع گوشی که در ستون Percent قابل رویت است، با یکدیگر اختلاف زیادی دارند. بنابراین توزیع احتمال یکسانی نخواهند داشت. ولی این گمان باید براساس آزمون فرض نیز سنجیده شده و به روش آزمون فرض آماری بیان شود.

برازش توزیع یکنواخت تک نمونه‌ای در SPSS

برای انجام آزمون برازش توزیع، فرضیاتی وجود دارد که با توجه به آن‌ها آماره آزمون تعیین شده و می‌توان از نرم‌افزار SPSS برای انجام محاسبات بهره برد. در ادامه شرایط را مشاهده می‌کنید.

1. مشاهدات نمونه تصادفی باید مستقل از یکدیگر باشند.
2. مقدار مورد انتظار (امید ریاضی) برای هر یک از گروه‌ها نباید صفر باشد. از طرفی نیز حداقلی برای هر گروه در این آزمون وجود دارد. به بیان دیگر باید کمتر از ۲۰ درصد گروه‌ها فراوانی کمتر از ۵ داشته باشند. در غیر اینصورت نتایج آزمون قابل اعتماد نیست.

برای اجرای دستور مقایسه توزیع گرو‌ه‌ها، مطابق تصویر زیر از فهرست Analysis گزینه Nonparametric Tests و سپس گزینه Legacy Dialog و در انتها نیز دستور Chi-Square را انتخاب کنید. در پنجره ظاهر شده فقط کافی است تنظیمات را مطابق با تصویر انجام دهید. این گام‌ها را مطابق با شماره‌های مورد نظر در تصویر می‌توانید پی بگیرید.

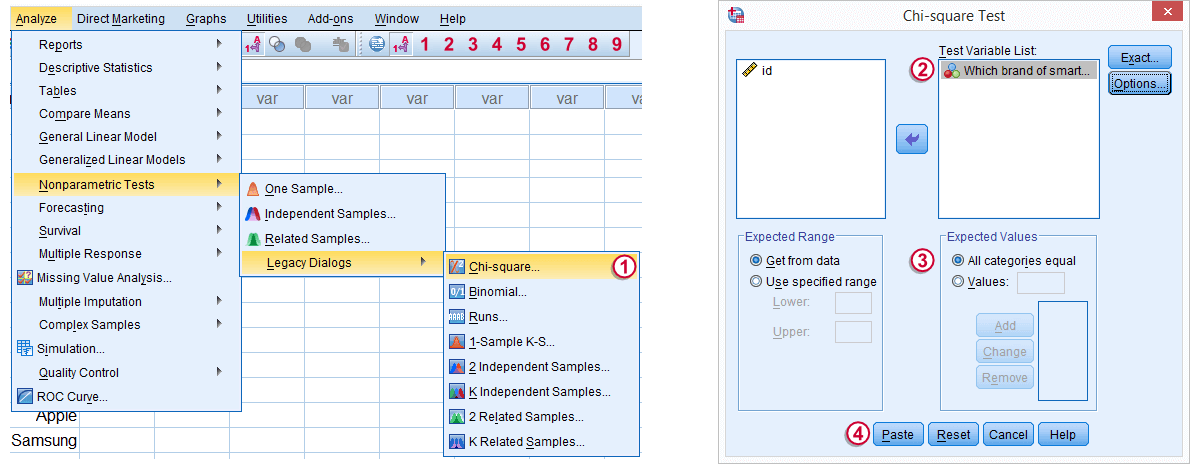
در پنجره Chi-Square Test در کادری که با شماره 2 مشخص شده است، متغیر مورد نظر برای انجام آزمون را قرار دهید. از طرفی برای تعیین مقدار مورد انتظار برای هر یک از گروه‌ها از کادر شماره 3 استفاده کنید. با توجه به اینکه می‌خواهیم فرض یکسان بودن درصدها را بین گروه‌ها در نظر بگیریم، در این قسمت All Categories equal را انتخاب کرده‌ایم. ویژگی‌های کادرهای Expected Range و Expected Values را به اختصار در ادامه توضیح خواهیم داد.

دامنه مورد انتظار (Expected Range)

هنگام اجرای این آزمون، فرض بر این است که هر مقدار منحصر به فرد در متغیری که در کادر Test Variable List قرار گرفته است، یک گروه را تشکیل می‌دهد. به این ترتیب با انتخاب Get from data، مقادیر منحصر به فرد متغیر به عنوان گروه‌های مجزا مشخص شده‌اند. ولی اگر می‌خواهید بعضی از مقادیر مربوط به متغیر را برای گروه‌بندی مشخص کنید، کافی است گزینه Use specified range را انتخاب و کران پایین و بالایی برای مقدار گروه‌ها را تعیین کنید. به این ترتیب مشاهداتی که خارج از گروه‌های مشخص شده باشند در محاسبات مربوط به آزمون کای ۲ به کار نمی‌روند. از همین رو اگر فرض کنیم، هفت مقادیر منحصر به فرد در متغیر وجود داشته باشد با مشخص کردن مقدار 1 در کادر Lower و 4 در Upper مشاهدات و محاسبات را برای این چهار گروه محدود کرده‌اید.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

مقادیر مورد انتظار (Expected Values)

به طور پیش‌فرض (با انتخاب گزینه All categories equal)، برای گروه‌های تعیین شده در دامنه مورد انتظار (Expected Range) درصد یا فراوانی‌ها به طور یکسان در نظر گرفته می‌شود. اگر لازم است که برای مقدار مورد انتظار هر گروه، تعداد یا درصدی مشخص شود کافی است مقدار مورد نظر را در کادر Values‌ وارد کرده و دکمه Add را بزنید. چنانچه احتیاج به تغییر مقداری دارید، پس از انتخاب آن و تغییر مقدار، از دکمه Change استفاده کنید. همچنین انتخاب دکمه Remove بعد از انتخاب یک مقدار خاص، آن را از لیست مقادیر مورد انتظار حذف خواهد کرد. توجه داشته باشید که ترتیب قرارگیری این مقدارها متناسب با ترتیب مقدارهای متغیر باشد.

با فشردن دکمه OK نتایج ظاهر خواهند شد. البته با دکمه Paste‌ نیز می‌توانید دستورات مربوط به اجرای این تحلیل را در پنجره Syntax قرار دهید.

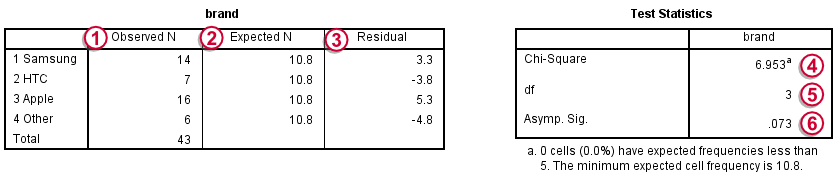
براساس شماره‌هایی که روی تصویر بالا مشاهده می‌کنید، فهرستی از توصیف خروجی‌ها تهیه کرده‌ایم تا تفسیر مناسبی از نتایج داشته باشیم.

1. تعداد مشاهدات در ستون Observed N برای هر گروه مشخص شده است. مشخص است که مجموع مشاهدات نیز برابر با ۴۳ است.
2. مقدار مورد انتظار برای هر یک از گروه‌ها نیز براساس محاسبه  $$\frac{43}{4}=10.8$$ بدست می‌آید.
3. باقیمانده نیز براساس اختلاف تعداد هر یک از گروه‌ها از مقدار مورد انتظار بدست می‌آید.
4. مقدار آماره کای ۲ نیز که توسط SPSS محاسبه شده است در این قسمت مشاهده می‌شود. بزرگ بودن این آماره به رد فرض صفر می‌انجامد. البته به جای مقایسه این آماره با مقدار صدک $$1-\alpha$$ام توزیع کای ۲ با درجه آزادی قید شده در شماره ۵، کافی است به مقدار Sig که در شماره ۶ دیده می‌شود اکتفا کنیم.
5. درجه آزادی توزیع کای ۲ متناسب با جدول فراوانی و تعداد گروه‌ها. این درجه آزادی یکی کمتر از تعداد گروه‌ها است. یعنی $$4-1=3$$
6. از آنجایی که تعداد مشاهدات در این جدول زیاد است از توزیع مجانبی و مقدار احتمال (p-Value) مجانبی استفاده شده است. از آنجایی که Asymp. Sig کمتر از احتمال خطای نوع اول یعنی $$\alpha=0.05$$ است، فرض صفر که هم توزیعی گروه‌ها بود، رد خواهد شد.

با توجه به نتیجه آزمون فرض مشخص است که تعداد فروش‌ها به نوع یا برند گوشی همراه بستگی دارد.

نکته: در پایین جدول Test Statistics به عنوان پانویس، متنی آورده شده است که نشانگر درصد یا تعداد خانه‌هایی از جدول فراوانی است که دارای فراوانی کمتر از ۵ هستند. از آنجایی که در داده‌های به کار رفته در این مثال چنین وضعیتی وجود ندارد، این درصد برابر صفر است. در نتیجه بدون محدودیت می‌توان به نتیجه آزمون اطمینان کرد.

برازش توزیع غیر یکنواخت تک نمونه‌ای در SPSS

در اینجا حالتی را در نظر می‌گیریم که گروه‌ها دارای توزیع یکنواخت نیستند. بنابراین نسبت‌های بین گروه‌ها یکسان نخواهد بود. در این صورت فرض صفر را به صورت زیر خواهیم نوشت. توجه کنید که منظور از $$p_i$$‌ درصد گروه $$i$$ام و $$q_i$$ درصد مورد انتظار برای آن گروه است.

$$\large \begin{cases}H_0: & p_1=q_1, p_2=q2,\cdots =p_k=q_k\\ \large H_1: & \text{There are some different in p's and q's. }\end{cases}$$

براساس مثال قبلی که درصد فروش انواع گوشی‌ها را مورد بررسی قرار داده بود، می‌خواهیم دست به یک آزمون جدید بزنیم. قصد داریم نشان دهیم که برند «سامسونگ» (Samsung) و «اپل» (Apple) سهم یکسان و حدود 15 واحد دارند. از طرفی HTC و بقیه نیز هر یک به تنهایی 6.5 واحد انتظار فروش دارند. تنظیمات مربوط به اجرای چنین آزمونی را مطابق با تصویر زیر انجام خواهیم داد.

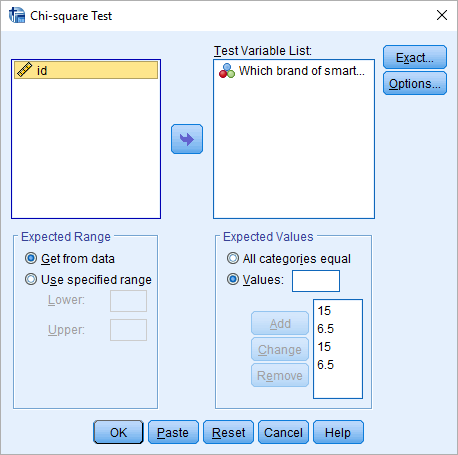
نکته: مجموع مقادیری که در بخش Expected Values وارد می‌کنید باید با تعداد مشاهدات برابر باشد. همچنین اگر مقدار مورد انتظار برای هر گروه را به صورت درصدی (مقدارهای کوچکتر از یک) بیان می‌کنید، توجه داشته باشید که مجموع درصدها باید 1 باشد.

همانطور که دیده می‌شود، تعداد (یا درصد) مربوط به هر گروه باید به ترتیب مقدارهای مربوط به متغیر مربوطه ثبت شده باشند. با انتخاب گزینه Exact نیز می‌توانید، همانطور که در تصویر زیر دیده می‌شود، مقدار دقیق احتمال را درخواست کنید،

خروجی به این ترتیب به صورت زیر درخواهد آمد. مشخص است که با توجه به مقدار $$Exact \; Sig. 0.977$$ در جدول Test Statistics، فرض صفر در سطح احتمال خطای $$\alpha=0.05$$ رد نخواهد شد. بنابراین به نظر می‌رسد که درصدهای انتخابی برای هر یک از دسته یا گروه تلفن‌های همراه مطابق با پیش‌بینی ما بوده است.

اگر لازم باشد می‌توانید از کد زیر برای اجرای این دستور در پنجره Syntax استفاده کنید.

برازش توزیع یکنواخت یا غیر یکنواخت روی گروهی از نمونه‌ها در SPSS

ممکن است به لحاط تکنیکی لازم باشد که فقط آزمون برازش توزیع را بین گروه‌های خاصی از نمونه‌ها اجرا کنیم. در این حالت بهتر است بر اساس کادر Expected Range مقداری که نمایانگر گروه‌ها هستند را مشخص کنید. البته توجه داشته باشید که در این حالت باید ترتیب گروه‌ها رعایت شود زیرا فقط می‌توان کران پایین و بالا برای مقدار گروه‌ها را وارد کرد.

فرض کنید در مثال قبل می‌خواهیم نشان دهیم که درصد تعداد فروش گوشی اپل (Apple) و دیگر برندها (Other) یکی است. با توجه به تصویر زیر مراحل را طی کرده و تنظیمات را انجام می‌دهیم. توجه دارید که مقدار 3 برای گوشی Apple‌ و مقدار 4 برای گوشی‌های دیگر در نظر گرفته شده است.

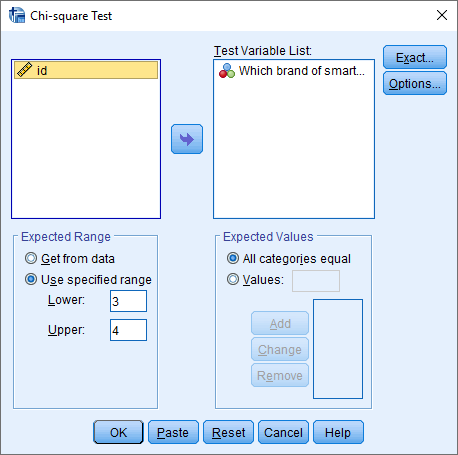
با فشردن دکمه OK خروجی مطابق تصویر زیر خواهد بود. دیده می‌شود که Asymp Sig برابر با $$0.033$$ است پس فرض برابری نسبت‌ها در سطح آزمون $$0.05$$ رد می‌شود. شاید در این حالت بتوان گفت که درصد یا تعدادی که برای نسبت بین تلفن‌های همراه اپل با دیگر برندها در نظر گرفته‌اید معقول به نظر می‌رسد.

کد لازم برای اجرای این دستور در Syntax در ادامه قابل مشاهده است.

تنظیمات بیشتر

اگر لازم باشد در مورد نمایش محاسبات آمار توصیفی و صدک‌های داده‌ها و همچنین مقادیر گمشده (Missing Values) تصمیمی گرفته شود، از دکمه Options در پنجره اصلی استفاده کنید. به این ترتیب در پنجره Chi-square test: Option با انتخاب گزینه‌های Descriptive آماره‌های توصیفی شامل میانگین، حداقل، حداکثر و انحراف معیار نمایش داده خواهد شد. با انتخاب Quartiles چارک‌ها (شامل میانه) نیز ظاهر خواهند شد.

همچنین انتخاب Exclude cases test-by-test باعث می‌شود در صورت استفاده از بیش از یک متغیر، فقط مشاهداتی به کار گرفته شوند که در همه متغیرها، مقدار دارند. به این معنی که اگر با توجه به وجود دو متغیر، مشاهده‌ای فقط در متغیر اول، دارای مقدار گمشده است، در آزمون توزیع مربوط به متغیر آن مشاهده در نظر گرفته نخواهد شد. همچنین گزینه Exclude cases listwise از مشاهدات دارای مقدار گمشده در همه آزمون‌ها صرف نظر خواهد کرد.

اگر به یادگیری مباحث مشابه مطلب بالا علاقه‌مند هستید، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• مجموعه آموزش‌های SPSS
• مجموعه آموزش‌های برنامه نویسی متلب برای علوم و مهندسی
• متغیر تصادفی و توزیع کای 2 (Chi Squared) — مفاهیم و کاربردها
• آزمون لون (Levene’s Test) برای برابری واریانس ها در SPSS — راهنمای کاربردی
• بوت استرپ (Bootstrapping) در SPSS — راهنمای کاربردی
• متغیر دو وضعیتی (Dichotomous) در SPSS — راهنمای کاربردی

^^