آزمون نرمال بودن داده (Normality Test) – پیاده سازی در پایتون

یکی از مسائل مهم در تحلیل آماری داده‌ها، انتخاب بین روش‌های پارامتری یا ناپارامتری به منظور انجام محاسبات و استنباط آماری است. هر چند روش‌های ناپارامتری ساده‌تر هستند ولی استفاده از آن‌ها در اکثر مواقع باعث می‌شود که نتایج تحلیل‌ها توان کمتری نسبت به روش‌های مشابه پارامتری داشته باشد. بنابراین اگر بتوانیم با آزمون نرمال بودن داده (Normality Test)، توزیع آن‌ها را گاوسی یا نرمال فرض کنیم، بهتر است که از روش‌های پارامتری استفاده کنیم. در این نوشتار به بررسی نحوه اجرای آزمون نرمال بودن داده (Normality Test) پرداخته و برای محاسبات از زبان برنامه‌نویسی پایتون و کتابخانه SciPy استفاده خواهیم کرد. در ضمن با استفاده از شبیه‌سازی داده‌ها، نرمال بودن آن‌ها را با روش‌هایی که معرفی شده‌اند مورد بررسی قرار می‌دهیم.

به منظور آشنایی بیشتر با توزیع نرمال و خصوصیات آن بهتر است مطلب توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها را مطالعه کنید. همچنین خواندن نوشتار آمار پارامتری و ناپارامتری — انتخاب روش های تحلیل نیز ضروری به نظر می‌رسد. همچنین مطالعه مطلب نمودار چندک چندک (Q-Q plot) — به زبان ساده نیز خالی از لطف نیست.

آزمون نرمال بودن داده (Normality Test)

در روشهای آمار پارامتری فرض بر این است که داده‌ها دارای توزیع شناخته شده و معینی هستند. در بیشتر موارد در آمار کلاسیک این توزیع برای داده‌ها، توزیع، گاوسی یا نرمال در نظر گرفته می‌شود. ولی اگر توزیع این داده‌ها گاوسی یا نرمال نباشد، پیش‌فرض‌های مربوط به آزمون‌ها و تحلیل‌های آمار پارامتری (Parametric Methods) و کلاسیک نقض شده و باید از روش‌های آماری غیرپارامتری یا ناپارامتری (Non Parametric Methods) استفاده کرد. ولی سوال در اینجا این است که چگونه از نرمال بودن داده‌ها مطلع شویم؟

خوشبختانه روش‌های زیادی به منظور سنجش و آزمودن نرمال بودن داده (Normality Test) وجود دارد که می‌توان از آنها استفاده کرد. البته از آنجایی که در این بین از آزمون آماری و مقدار احتمال (P-value) صحبت به میان می‌آید بهتر است در مورد هر یک از این اصطلاحات در نوشتارهای آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات و مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری اطلاعاتی کسب کنید تا مفاهیم و روش‌های ذکر شده در این مطلب را بهتر درک کنید.

فرض نرمال بودن

بخش عمده‌ای از تحلیل‌های آماری مربوط به متغیرهای تصادفی و جوامع با توزیع نرمال است. اما اگر داده‌ها دارای توزیع نرمال نبوده ولی شما از روش‌های پارامتری برمبنای توزیع نرمال استفاده کنید، ممکن است این یافته‌های شما در طرح تحقیقاتی‌ و تجزیه و تحلیل آماری داده‌ها، گمراه کننده یا اشتباه باشد. در نتیجه انجام آزمون نرمال بودن یا تایید فرض نرمال بودن داده‌ها یک نکته کلیدی در تصمیم‌گیری برای انتخاب روش‌ برای استنباط آماری برمبنای نمونه‌های تصادفی است. این تصمیم را به شرح زیر خلاصه کرده‌ایم:

اگر جامعه آماری دارای توزیع نرمال باشد، روش‌های پارامتری و اگر توزیع داده‌ها نامشخص (غیرنرمال) باشد، روش‌های ناپارامتری به کار گرفته می‌شوند.

البته ممکن است با کمی ساده‌گیری (بخصوص اگر عدم تقارن یا چولگی زیاد نباشد) فرض کنیم که داده‌ها دارای توزیع نرمال هستند تا از روش‌های پارامتری که بخصوص در آزمون‌های آماری از «توان آزمون» (Power Test) بیشتری برخوردارند، استفاده کنیم. گاهی نیز می‌توان با استفاده از رابطه یا تبدیلاتی، داده‌های غیرنرمال را به نرمال تغییر شکل داد و براساس آن‌ها استنباط و روش‌های پارامتری را به کار گرفت.

نکته: قضیه حد مرکزی  (Centeral Limit Theorem) یا CLT نشان می‌دهد که در صورت بزرگ بودن حجم نمونه می‌توان توزیع میانگین نمونه‌های تصادفی را نرمال فرض کرد ولی زمانی که توزیع مشخص نبوده و حجم نمونه هم به دلایل مختلف کوچک باشد، لازم است که نرمال بودن بررسی شده و در صورتی که شرایط نرمال بودن محقق نشد، از روش‌های ناپارامتری استفاده کرد.

برای آزمون نرمال بودن داده (Normality Test) از دو روش مختلف می‌توان استفاده کرد که در این نوشتار به آن‌ها اشاره خواهیم کرد.

• روش‌های تصویری (Graphical Methods): بوسیله ترسیم چندک‌ها یا مقدار احتمالات تجمعی برای هر نقطه از داده‌ها و مقایسه آن با توزیع نرمال، می‌توان به هم‌توزیعی جامعه آماری با توزیع نرمال پی‌برد.
• روش‌های آزمون فرض (Statistical Testing): در این گونه روش‌ها توسط آماره آزمون و فرضیه‌های آماری و به کمک نمونه تصادفی نسبت به رد یا تایید فرض صفر که همان نرمال بودن جامعه آماری است، رای می‌دهیم. واضح است که در این روش، ملاک اصلی ما مقدار احتمال (P-value) یا آماره آزمون و مقایسه آن با مقدار بحرانی آزمون است که توسط نمونه تصادفی حاصل شده.

در سه بخش از پروژه‌های یادگیری ماشین (Machine Learning) ممکن است با بحث نرمال بودن داده‌ها بخصوص در مدل‌سازی براساس متغیرهای مستقل و وابسته مواجه شوید.

• داده‌های ورودی (متغیر پاسخ) برای برازش مدل‌های آماری
• ارزیابی مدل براساس پیش‌فرض‌های مدل‌سازی (نرمال بودن باقی‌مانده‌ها)
• ارزیابی داده‌ها (متغیرها) به منظور انجام آزمون فرض آماری پارامتری

قبل از آنکه در مورد آزمون نرمال بودن داده (Normality Test) صحبت به میان آوریم، بهتر است خصوصیات داده‌هایی با توزیع نرمال را مرور کنیم.

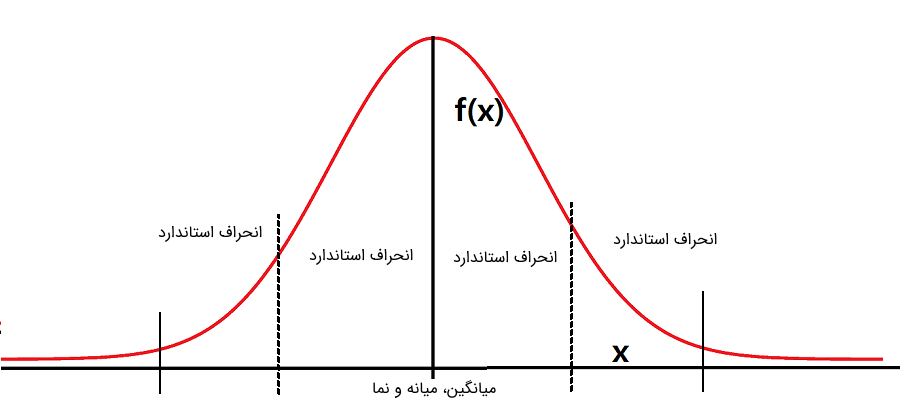
در توزیع نرمال، منحنی مربوط به توزیع یا نحوه تقسیم احتمال برای نواحی مختلفی از داده‌ها به شکل یک زنگ بزرگ (زنگی شکل یا Bell Curve) است. قله این منحنی، میانگین، میانه و نما را مشخص می‌کند. از طرفی کاملا دیده می‌شود که این منحنی نسبت به نقطه مرکزی یعنی همان میانگین (یا میانه یا نما) متقارن است. همینطور پراکندگی حول میانگین نیز با انحراف معیار یا پارامتر دوم توزیع نرمال متناسب است. چنین منحنی که در تصویر زیر مشاهده می‌شود، نحوه تغییرات شکل فراوانی (تابع چگالی احتمال) را برای توزیع نرمال نشان می‌دهد.

از طرفی احتمال اینکه داده‌ای در بازه یک انحراف استاندارد از میانگین فاصله داشته باشد حدود 68 درصد است. همچنین احتمال اینکه در بازه ۲ انحراف استاندارد از میانگین داده‌ای مشاهده شود، تقریبا 95 درصد است. همین احتمال برای فاصله ۳ انحراف استاندارد تقریبا همه مقادیر را پوشش داده و حدود 99.7 درصد احتمال دارد که داده‌ای در این فاصله مشاهده شود. به این ترتیب مشخص است که احتمال اینکه داده‌ای بیشتر از سه انحراف استاندارد از میانگین فاصله داشته باشد بسیار ناچیز و تقریبا برابر با صفر خواهد بود.

مجموعه داده با توزیع نرمال

به کمک دستورات زیر در پایتون، یک مجموعه داده تصادفی از توزیع نرمال به حجم ۱۰۰ و با میانگین ۵۰ و انحراف استاندارد ۵ تولید می‌کنیم. این کار را به کمک تابع randn انجام داده‌ایم که از توزیع نرمال استاندارد (توزیع نرمال با میانگین صفر و واریانس ۱) نمونه تصادفی تولید می‌کند. با ضرب کردن مقدارهای شبیه‌سازی شده در انحراف استاندارد یعنی ۵ و جمع حاصل با ۵۰، میانگین داده‌های تولید شده را به ۵۰ و انحراف استاندارد ۵ تبدیل کرده‌ایم.

1# generate gaussian data
2from numpy.random import seed
3from numpy.random import randn
4from numpy import mean
5from numpy import std
6# seed the random number generator
7seed(1)
8# generate univariate observations
9data = 5 * randn(100) + 50
10# summarize
11print('mean=%.3f stdv=%.3f' % (mean(data), std(data)))

در انتهای کد، مقادیر میانگین و انحراف استاندارد نمونه حاصل را محاسبه کرده‌ایم. انتظار داریم که برای این نمونه تصادفی میانگین و انحراف استاندارد به جامعه مورد نظر یعنی نرمال با میانگین ۵۰ و انحراف استاندارد ۵، نزدیک باشد. پس از انجام محاسبات، نتیجه به صورت زیر بدست می‌آید.

1mean=50.303 stdv=4.426

همانطور که انتظار داشتیم، مقدار میانگین $$mean=50.303$$ و انحراف استاندارد $$stdv=4.426$$ به مقدارهای واقعی یعنی ۵۰ و ۵ نزدیک هستند.

روش‌های تصویری بررسی فرض نرمال

هر چند روش‌های تصویری نسبت به روش‌های آزمون فرض، کارایی کمتری دارند ولی به هر حال برای بررسی سریع و راحت‌تر، بسیار مناسب بوده و روش تفسیر آن‌ها ساده‌تر است. در این قسمت دو روش بررسی تصویری آزمون نرمال بودن داده (Normality Test) یعنی هیستوگرام یا نمودار فراوانی و نمودار چندک-چندک Q-Q plot‌ مورد بررسی قرار می‌گیرد.

فیلم آموزش مبانی و روش های اقتصاد سنجی با ایویوز Eviews در فرادرس

کلیک کنید

نمودار فراوانی (Histogram)

نمودار فراوانی، به مانند جدول فراوانی (Frequency Table) است و روشی برای نمایش شکل توزیع تجربی داده‌ها است. به این ترتیب با مقایسه نمودار فراوانی با توزیع نرمال می‌توان پی به نرمال بودن داده‌ها برد. هرچه شکل نمودار فراوانی به توزیع گاوسی یا زنگی شکل نزدیکتر باشد، داده‌ها برازش بیشتری با توزیع نرمال دارند.

قطعه کد زیر به منظور ترسیم نمودار فراوانی برای داده‌های شبیه‌سازی شده ایجاد شده است. برای ترسیم این نمودار از کتابخانه matplotlip و تابع ()hist استفاده شده است. تعداد تقسیمات برای تعیین فاصله روی محور افقی به طور خودکار توسط تابع ()hist صورت گرفته است.

1# histogram plot
2from numpy.random import seed
3from numpy.random import randn
4from matplotlib import pyplot
5# seed the random number generator
6seed(1)
7# generate univariate observations
8data = 5 * randn(100) + 50
9# histogram plot
10pyplot.hist(data)
11pyplot.show()

در تصویر زیر نمودار فراوانی تولید شده توسط کد پایتون نمایش داده شده است. مشخص است که قله نمودار در نقطه حدود ۵۰ که همان نما است رخ داده و فراوانی این مقدار نیز 20 است. مقدار نما تقریبا به مقدار میانگین و میانه نیز نزدیک است. پس می‌توان توزیع را حداقل براساس معیارهای مرکزی شبیه توزیع نرمال در نظر گرفت. همانطور که می‌دانید، میانگین مرکز ثقل، میانه، مرکز تقارن و نما نیز نقطه‌ای است که بیشترین فراوانی در آن وجود دارد.

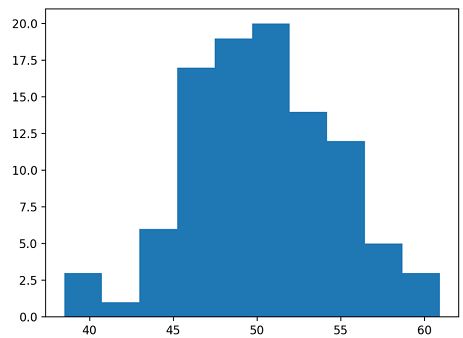
با توجه به تصویر زیر، به نظر می‌رسد که داده‌ها (به جز در دم سمت چپ) دارای توزیع نرمال هستند. به این ترتیب به کمک تکنیک تصویری آزمون نرمال بودن داده (Normality Test) را انجام دادیم.

نمودار چندک چندک یا Q-Q plot

یکی دیگر از روش‌های تصویری به منظور بررسی توزیع نرمال، استفاده از نمودار چندک-چندک یا Q-Q plot است. در این نمودار چندک‌های توزیع تجربی داده‌ها در مقابل چندک‌های نرمال ترسیم می‌شود. هر نقطه از این نمودار به صورت زوج مرتب خواهد بود که مولفه اول مربوط به مقدار چندک توزیع نرمال و مولفه دوم نیز چندک براساس توزیع تجربی داده‌ها است. به این ترتیب رسم این نقاط در مختصات دکارتی، می‌تواند روشی برای تشخیص نرمال بودند توزیع داده‌ها باشد.

کدهای زیر به منظور ترسیم این نمودار در نظر گرفته شده است. برای رسم نمودار Q-Q plot از کتابخانه statsmodels و تابع qqplot استفاده شده است.

1# QQ Plot
2from numpy.random import seed
3from numpy.random import randn
4from statsmodels.graphics.gofplots import qqplot
5from matplotlib import pyplot
6# seed the random number generator
7seed(1)
8# generate univariate observations
9data = 5 * randn(100) + 50
10# q-q plot
11qqplot(data, line='s')
12pyplot.show()

اگر نقاط ترسیمی، به خطی که نشانگر نیمساز ربع اول است، نزدیک باشد، رای به نرمال بودن توزیع داده‌ها خواهیم داد. در غیر اینصورت نمی‌توانیم توزیع تجربی داده‌ها و در نتیجه توزیع جامعه آماری را نرمال در نظر بگیریم. به این ترتیب روشی برای آزمون نرمال بودن داده (Normality Test) ایجاد کرده‌ایم.

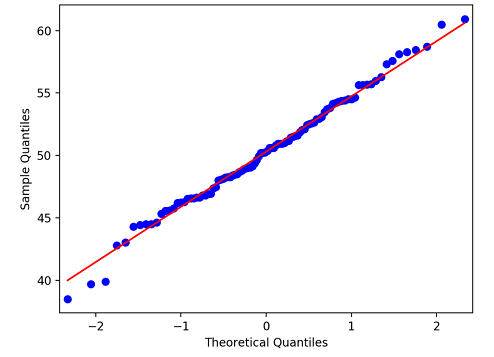
همانطور که در تصویر بالا دیده می‌شود، برای داده‌های شبیه‌سازی شده، رای به نرمال بودن خواهیم داد. البته این چیزی است که از قبل انتظار داشتیم زیرا نمونه تصادفی از توزیع نرمال تولید شده بود. به این ترتیب آزمون نرمال بودن داده (Normality Test) را به کمک نمودار Q-Q plot انجام دادیم.

آزمون‌های آماری بررسی فرض نرمال

روش‌ها و آزمون‌های آماری زیادی برای تشخیص هم‌توزیعی داده‌ها وجود دارد. به این ترتیب می‌توانیم براساس نمونه تصادفی و مقایسه آن با توزیع‌های دلخواه، آماره آزمون را محاسبه و نسبت به هم‌توزیعی توزیع تجربی داده‌ها و توزیع مورد نظر تصمیم بگیریم. در اینجا به آزمون‌هایی اشاره می‌کنیم که برای بررسی توزیع داده‌ها با توزیع نرمال مناسب است و به این ترتیب آزمون نرمال بودن داده (Normality Test) را اجرا کنیم.

البته به این نکته نیز توجه داشته باشید که هر یک از آزمون‌های معرفی شده احتیاج به محقق شدن پیش‌فرض‌هایی دارد که در ادامه توضیح داده خواهد شد. در این نوشتار به سه نوع آزمون متداول خواهیم پرداخت. البته بهتر است قبل از پرداختن به این آزمون‌ها مقدماتی در مورد آزمون فرض آماری نیز گفته شود.

فرض آماری: گزاره‌ای که براساس آن می‌خواهیم نسبت به رفتار جامعه آماری اطلاع پیدا کنیم فرض آماری گفته می‌شود. برای مثال می‌توان فرض صفر یا $$H_0$$ را به صورت زیر در نظر گرفت:

$$\large H_0: \text{Data have normal distribution}$$

به این ترتیب در فرض صفر، نرمال بودن داده‌ها قرار گرفته است. در صورتی که فرض صفر توسط نمونه تصادفی رد شود، نتیجه خواهیم گرفت که نمی‌توان توزیع جامعه آماری که نمونه از آن گرفته شده را نرمال فرض کرد.

آماره آزمون: کمیتی که براساس نمونه تصادفی محاسبه شده و براساس مقدار آن و ناحیه بحرانی (Critical Area) نسبت به رد یا تایید فرض صفر اقدام می‌کنیم.

مقدار احتمال (P-value): از مقدار احتمال به منظور بررسی تایید یا رد فرض صفر استفاده می‌شود. اگر مقدار احتمال کمتر از احتمال خطای نوع اول ($$\alpha$$) باشد، فرض صفر را رد می‌کنیم. در غیر اینصورت نمونه تصادفی دلیلی برای رد فرض صفر در اختیارمان قرار نمی‌دهد.

در ادامه براساس این توضیحات، آزمون‌های شاپیرو ویلک (Shapiro-Wilk's Test)، آزمون کای ۲ دآگوستینو (D’Agostino’s K^2 Test) و اندرسون دارلینگ (Anderson-Darling Test) را مورد بررسی قرار می‌دهیم که به عنوان محکی برای آزمون نرمال بودن داده (Normality Test) به کار می‌روند.

آزمون شاپیرو ویلک (Shapiro-Wilk's Test)

آزمون آماری شاپیرو-ویلک، برمبنای آماره‌ای با همین نام، ملاکی برای مطابقت توزیع داده‌های با توزیع نرمال فراهم می‌کند. آماره این آزمون براساس مقادیر مرتب شده داده‌ها عمل می‌کند و از آماره ترتیبی (Order Statistics)، میانگین (Mean) و واریانس (Variance) داده‌ها برای محاسبات استفاده می‌کند. این روش آزمون بر اساس تحقیقات دو دانشمند «ساموئل شاپیرو» (Samuel Sanford Shapiro) آمارشناس آمریکایی و «مارتین ویلک» (Martin Wilk) آمارشناس کانادایی توسعه و به کار گرفته شد.

فرض صفر در این آزمون، نرمال بودن داده‌ها است و اگر آماره آزمون مقدار بزرگی باشد، فرض صفر رد می‌شود. البته در این میان مقدار خطای نوع اول ($$\alpha$$) نیز باید در نظر گرفته شود. اگر مقدار احتمال (P-value) کوچکتر از مقدار $$\alpha$$ باشد، فرض صفر رد شده و در غیر اینصورت دلیلی بر رد فرض صفر نخواهیم داشت.

محاسبات مربوط به آماره شاپیرو-ویلک در پایتون توسط تابع shapiro از کتابخانه SciPy صورت می‌گیرد. در کد زیر برای داده‌های شبیه‌سازی شده از توزیع نرمال با میانگین ۵۰ و انحراف معیار ۵، آزمون شاپیرو-ویلک صورت گرفته است. مقدار احتمال خطای نوع اول در این برنامه همان 0.05 در نظر گرفته شده و با مقایسه آن با مقدار احتمال (P-value) تصمیم به رد یا عدم رد فرض صفر می‌زنیم.

1# Shapiro-Wilk Test
2from numpy.random import seed
3from numpy.random import randn
4from scipy.stats import shapiro
5# seed the random number generator
6seed(1)
7# generate univariate observations
8data = 5 * randn(100) + 50
9# normality test
10stat, p = shapiro(data)
11print('Statistics=%.3f, p=%.3f' % (stat, p))
12# interpret
13alpha = 0.05
14if p > alpha:
15	print('Sample looks Gaussian (fail to reject H0)')
16else:
17	print('Sample does not look Gaussian (reject H0)')

خروجی این برنامه در ادامه قابل مشاهده است. همانطور که دیده می‌شود، آماره آزمون کوچک بوده (البته با مقایسه با توزیع شاپیرو-ویلک) و از طرفی هم مقدار احتمال $$p =0.822$$ بزرگتر از احتمال خطای نوع اول است، در نتیجه نمونه تصادفی دلیل بر رد فرض صفر ارائه نکرده است. این عبارت در انگلیسی به صورت (Sample looks Gaussian (fail to reject H0 نمایش داده شده است. در نتیجه دلیلی نداریم که توزیع داده‌ها را نرمال فرض نکنیم.

1Statistics=0.992, p=0.822
2Sample looks Gaussian (fail to reject H0)

به این ترتیب آزمون نرمال بودن داده (Normality Test) را به کمک آماره شاپیرو-ویلک انجام دادیم.

آزمون دآگوستینو (D’Agostino’s K² Test)

آماره آزمون کای ۲ دآگوستینو، برمبنای محاسبه چولگی و کشیدگی داده‌ها عمل کرده و نرمال بودن آن‌ها را تشخیص می‌دهد. این آماره توسط رالف دآگوستینو (Ralph D'Agostino) معرفی شده است.

همانطور که می‌دانیم، چولگی (Skewness) میزان انحراف افقی توزیع را نسبت به توزیع نرمال می‌سنجد. اگر توزیعی دارای چولگی باشد، دم توزیع به سمت راست یا به سمت چپ تمایل داشته و نمودار توزیع آن نامتقارن خواهد بود. از طرفی کشیدگی (Kurtosis) نیز میزان انحراف عمودی توزیع داده‌ها را نسبت توزیع نرمال می‌سنجد. هر چه توزیع کشیده‌تر باشد، مقدار فراوانی در مرکز بیشتر بوده و در دم‌ها کمتر از توزیع نرمال است. به این ترتیب با استفاده از این دو معیار می‌توان مطابقت توزیع داده‌ها را با توزیع نرمال اندازه‌گیری کرد.

در پایتون برای محاسبه آماره آزمون کای ۲ دآگوستینو، از تابع ()normaltest ‌از کتابخانه SciPy استفاده می‌شود. خروجی‌های این آزمون مقدار آماره و همچنین مقدار احتمال (P-value) است. در ادامه به کدی اشاره شده است که برای سنجش نرمال بودن داده‌های شبیه‌سازی شده از توزیع نرمال با میانگین ۵۰ و انحراف معیار ۵ بر اساس آماره و آزمون کای ۲ دآگوستینو به کار رفته است.

1# D'Agostino and Pearson's Test
2from numpy.random import seed
3from numpy.random import randn
4from scipy.stats import normaltest
5# seed the random number generator
6seed(1)
7# generate univariate observations
8data = 5 * randn(100) + 50
9# normality test
10stat, p = normaltest(data)
11print('Statistics=%.3f, p=%.3f' % (stat, p))
12# interpret
13alpha = 0.05
14if p > alpha:
15	print('Sample looks Gaussian (fail to reject H0)')
16else:
17	print('Sample does not look Gaussian (reject H0)')

حاصل محاسبات و خروجی برنامه در ادامه مشاهده می‌شود. با توجه به کوچک بودن آماره آزمون ($$Statistics=0.102$$) فرض صفر که نرمال بودن داده‌ها است،‌ رد نمی‌شود. بنابراین نمونه تصادفی دلیلی بر رد فرض صفر ارائه نکرده است. به این ترتیب آزمون نرمال بودن داده (Normality Test) را به کمک آماره و آزمون کای ۲ دآگوستینو انجام دادیم.

1Statistics=0.102, p=0.950
2Sample looks Gaussian (fail to reject H0)

نکته: با توجه به بزرگ بودن مقدار احتمال ($$p=0.950$$) می‌توان گفت در هر سطح از آزمون، فرض صفر رد نخواهد شد مگر آنکه خطای نوع اول را بزرگتر از 0.95 در نظر بگیریم که اصلا کار عاقلانه‌ای نیست.

آزمون اندرسون دارلینگ (Anderson-Darling)

آزمون اندرسون-دارلینگ یک آزمون آماری است که برای ارزیابی نرمال بودن جامعه آماری که نمونه تصادفی از آن گرفته شده است به کار می‌رود. نام‌های «تئودور اندرسون» (Theodore Wilbur Anderson) و «دونالد دارلینگ» (Donald Darling) مشخص می‌کند که این دو ریاضی‌دان و آمارشناس آمریکایی، در ایجاد و توسعه این آزمون نقش داشته‌اند.

فیلم آموزش تجزیه و تحلیل داده های مالی با پایتون – بخش دوم + گواهینامه در فرادرس

کلیک کنید

این آزمون می‌تواند برای بررسی اینکه آیا توزیع جامعه آماری نرمال است یا خیر مورد استفاده قرار گیرد. واضح است که این کار توسط نمونه تصادفی از داده‌ها آن جامعه صورت می‌پذیرد. این آزمون یک نسخه اصلاح شده از یک آزمون آماری ناپارامتری دیگر به نام آزمون کولموگروف-اسمیرنوف (Kolmogorov-Smirnov) است.

یکی از ویژگی های تست اندرسون-دارلینگ در پایتون این است که علاوه بر مقدار احتمال (P-value) لیستی از مقادیر مهم را نیز محاسبه و نمایش می‌دهد که می‌تواند مبنایی برای تفسیر دقیق‌تر از نتیجه باشد. تابع anderson از کتابخانه SciPY در پایتون برای انجام آزمون نرمال بودن براساس آماره آزمون اندرسون-دارلینگ به کار می‌رود. نمونه تصادفی و نام توزیع مورد نظر به عنوان پارامترهای این تابع به کار می‌روند. به طور پیش فرض، نوع توزیع مورد نظر، نرمال در نظر گرفته می‌شود. به همین دلیل در کدی که در ادامه مشاهده می‌کنید، در تابع anderson، نوع توزیع مشخص نشده است. کد کامل به منظور محاسبات آزمون اندرسون-دارلینگ برای داده‌های شبیه‌سازی شده، در ادامه نشان داده شده است.

1# Anderson-Darling Test
2from numpy.random import seed
3from numpy.random import randn
4from scipy.stats import anderson
5# seed the random number generator
6seed(1)
7# generate univariate observations
8data = 5 * randn(100) + 50
9# normality test
10result = anderson(data)
11print('Statistic: %.3f' % result.statistic)
12p = 0
13for i in range(len(result.critical_values)):
14	sl, cv = result.significance_level[i], result.critical_values[i]
15	if result.statistic < result.critical_values[i]:
16		print('%.3f: %.3f, data looks normal (fail to reject H0)' % (sl, cv))
17	else:
18		print('%.3f: %.3f, data does not look normal (reject H0)' % (sl, cv))

خروجی این دستورات، به صورت زیر خواهند بود. مقدار آماره آزمون را در خط اول مشاهده می‌کنید که برابر با $$Statistics: 0.220$$ است. از طرفی فرض صفر ($$H0$$) به ازاء مقدارهای مختلف سطح معنی‌داری (به صورت درصدی) و ناحیه بحرانی رد نمی‌شود. مشخص است که همه مقدارهای بحرانی برای سطح معنی‌داری از 15٪ تا 1٪ (یعنی از 0.15 تا 0.01) از مقدار آماره آزمون بزرگتر هستند پس فرض صفر رد نخواهد شد.

1Statistic: 0.220
215.000: 0.555, data looks normal (fail to reject H0)
310.000: 0.632, data looks normal (fail to reject H0)
45.000: 0.759, data looks normal (fail to reject H0)
52.500: 0.885, data looks normal (fail to reject H0)
61.000: 1.053, data looks normal (fail to reject H0)

البته از آنجایی که در بیشتر موارد سطح معنی‌داری آزمون را ۵٪ (0.05) در نظر می‌گیریم محاسبات انجام شده برای این میزان خطا را دنبال می‌کنیم. در لیست ظاهر شده در خط سوم این محاسبات دیده می‌شود و بر عدم رد فرض صفر تاکید دارد زیرا در سطح خطای ۵٪، ناحیه بحرانی بزرگتر از آماره آزمون است. به این ترتیب آزمون نرمال بودن داده (Normality Test) را به کمک آماره و آزمون اندرسون-دارلینگ انجام دادیم.

نکته: همانطور که دیده می‌شود، این روش، قوی‌تر از مقدار احتمال یا P-value عمل کرده و در چند سطح خطا، مقدار آماره آزمون را با ناحیه بحرانی مقایسه کرده است و نمونه تصادفی قادر به رد کردن فرض صفر در سطح‌های آزمون مختلف نبوده است.

چگونه آزمون مناسب را انتخاب کنیم

در این نوشتار به بررسی چند شیوه برای آزمون نرمال بودن داده (Normality Test) و تشخیص توزیع آماری جامعه پرداختیم. ولی چگونه باید از بین این روش‌ها، مناسب‌ترین تحلیل را برای داده‌های خود انتخاب کنیم؟

توصیه می‌کنیم در صورت لزوم از همه آن‌ها برای نمونه تصادفی خود استفاده کنید. اگر همه آن‌ها به اتفاق رای به داشتن توزیع نرمال برای داده‌هایتان دادند و نمونه تصادفی قادر به رد فرض صفر نشد، می‌توانیم تقریبا مطمئن باشیم که جامعه آماری که نمونه از آن گرفته شده است، دارای توزیع نرمال است.

ولی اگر آزمون‌ها نتیجه یکسانی نداشته باشند، کدام رای را صحیح در نظر بگیریم؟ متاسفانه این امر اغلب نیز اتفاق می‌افتد،‌ پس مواجه شدن با این وضعیت خیلی دور از انتظار هم نیست.

در این رابطه دو پیشنهاد وجود دارد تا بتوانید در مورد پاسخ این سوال، بهترین گزینه را داشته باشید.

بیشتر روش‌ها داده‌ها را غیرنرمال شناسایی می‌کنند؟

اگر بیشتر روش‌های تصویری و آزمون آماری (و نه همه آن‌ها) نشان دادند که داده‌های شما، نرمال نیستند، بهتر است به جای روش‌های پارامتری از روش‌های ناپارامتری برای تحلیل داده‌هایتان استفاده کنید زیرا در این صورت نتایج قابل اعتمادتر هستند.

البته ممکن است یکی از دلایلی که داده‌ها نرمال نبوده‌اند، شیوه غلط نمونه‌گیری باشد. همچنین استفاده از یک تبدیل مثل لگاریتم‌گیری یا محاسبه ریشه از داده‌ها ممکن است باعث نرمال شدن مقادیر تبدیل یافته شود. در نتیجه بهتر است پس از تبدیل، نتایج را از نظر نرمال بودن بررسی کرده و سپس به کمک این داده‌های تبدیل یافته، تحلیل‌های آماری را انجام داده و در نهایت نتیجه را با تبدیل معکوس گزارش کنید.

بعضی از روش‌ها، داده‌ها را غیرنرمال در نظر گرفته‌اند؟

اگر برخی از روش‌ها نشان دهند که نمونه از جامعه نرمال نیست و بعضی برعکس بیانگر نرمال بودن داده‌ها باشند، پس شاید این را بتوان نشانه‌ای از نرمال بودن تقریبی مشاهدات در نظر گرفت. در این بین رسم نمودارهای فراوانی یا Q-Q plot می‌تواند گزینه دیگری برای تشخیص نرمال بودن داده‌ها باشد. در صورتی که «چولگی (Skewness) یا «کشیدگی» (Kurtosis) داده‌ها زیاد نباشد،‌ می‌توان رای به نرمال بودن داده‌ها صادر کرد.

خلاصه و جمع‌بندی

در این نوشتار با مفهوم روش‌های پارامتری و ناپارامتری در تحلیل‌های آماری آشنا شدیم. همچنین مشخص کردیم که برای استفاده از روش‌های پارامتری که البته نسبت به روش‌های ناپارامتری پرتوان‌تر هستند، باید توزیع داده‌ها بررسی شده و آزمون نرمال بودن داده (Normality Test) مورد سنجش قرار گیرد. برای انجام این کار هم تکنیک‌های تصویری و هم مبتنی بر آزمون فرض را معرفی کرده و نرمال بودن داده را مورد بررسی قرار دادیم.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های برنامه‌نویسی پایتون
• توزیع‌های آماری — مجموعه مقالات جامع وبلاگ فرادرس
• متغیر تصادفی و توزیع برنولی — به زبان ساده
• توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها

^^