آزمون کولموگروف اسمیرنف (Kolmogorov-Smirnov) — پیاده سازی در SPSS

در آمار ناپارامتری، یکی از روشهای سنجش و آزمون مربوط به توزیع، «آزمون کولموگروف اسمیرنف» (Kolmogorov–Smirnov test) است. به کمک این آزمون، میتوان بوسیله یک نمونه تصادفی از جامعه آماری، مشخص کرد که آیا جامعه آماری از توزیع مورد نظر پیروی میکنند یا خیر! همچنین بوسیله این آزمون، امکان بررسی همتوزیعی در بین دو جامعه نیز وجود دارد. در این نوشتار به بررسی «آزمون کولموگروف اسمیرنف» و نحوه اجرای آن در نرمافزار آماری SPSS خواهیم پرداخت.
برای آشنایی بیشتر با شیوه انجام آزمونهای آماری بهتر است مطلب آزمون های فرض و استنباط آماری — مفاهیم و اصطلاحات را بخوانید. البته آگاهی از روشهای دیگر چنین آزمونهایی مانند آزمون نیکویی برازش (Goodness of Fit Test) و استقلال — کاربرد توزیع کای2 نیز خالی از لطف نیست.
آزمون کولموگروف اسمیرنف
«آزمون کولموگروف-اسمیرنف» یکی از روشهای بررسی همتوزیعی دو جامعه یا بررسی «برازش توزیع» (Goodness of Fit Test) است که گاهی به آن آزمون نیکویی برازش نیز میگویند. این آزمون بدون داشتن هیچ پیشفرضی، صورت میگیرد و به این ترتیب از گروه روشهای ناپارامتری محسوب میشود.
فرض کنید که دادههایی از انجام یک آزمایش فیزیکی در حالتی خاص جمعآوری کردهاید. به مجموعه این دادهها، گروه کنترل میگوییم. همین آزمایش را در شرایط دیگر نیز تکرار کردهاید. به این ترتیب میخواهیم بدانیم آیا تغییر شرایط، در نتایج حاصل شده، تاثیر گذار است یا خیر؟ این آزمون، نظیر مقایسه توزیع تجربی دو جامعه آماری است که بوسیله آزمون کولموگروف اسمیرنف قابل بررسی است.
روش دیگری که میتوان از آزمون کولموگروف-اسمیرنف استفاده کرد، مطابقت توزیع جامعه آماری با یک توزیع مشخص است که به آن «آزمون نیکویی برازش» (Goodness of Fit Test) میگویند. به این ترتیب اگر دادههای حاصل از یک آزمایشی فیزیکی را جمعآوری کرده باشیم و بخواهیم توزیع احتمال نتایج حاصل را با توزیع مثلا کوشی (Cauchy) مقایسه کنیم، میتوانیم از آزمون کولموگروف-اسمیرنف استفاده کنیم. به این ترتیب توزیع تجربی حاصل از نمونه را با توزیع کوشی مقایسه میکنیم.
مشخص است که برای انجام آزمون کولموگروف-اسمیرنف احتیاج به توزیع تجربی دادهها داریم. در ادامه به معرفی توزیع تجربی خواهیم پرداخت.
تابع توزیع تجربی (Empirical Distribution Function)
همانطور که از اسم «تابع توزیع تجربی» (Empirical Cumulative Distribution Function- ECDF) پیدا است، براساس مشاهدات و نتایج آزمایشهای تصادفی محاسبه میشود. از این تابع به عنوان برآوردگر «تابع توزیع احتمال تجمعی» (Cumulative Distribution Function- CDF) استفاده میشود.
حال اگر بخواهیم مقدار تابع توزیع تجربی را در نقطه برای مقادیر مختلف متغیر تصادفی محاسبه کنیم، از رابطه زیر کمک خواهیم گرفت.
مشخص است که منظور از تابع نشانگر است که مقدار آن برای برابر با ۱ و در غیراینصورت برابر با صفر خواهد بود.
نکته: در اینجا باید توجه داشت که مربوط به یک نمونه nتایی بوده که از یکدیگر مستقل هستند. همچنین هنگام محاسبه تابع توزیع تجربی باید این مقادیر از کوچک به بزرگ مرتب شده سپس تابع توزیع محاسبه شود.
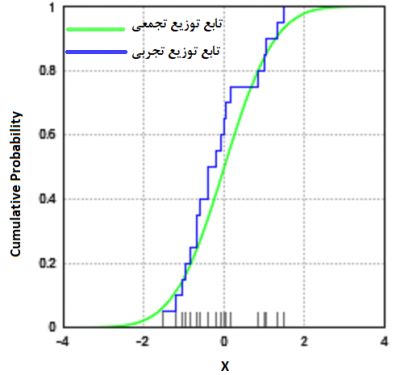
در تصویر بالا یک نمونه از تابع توزیع تجربی به همراه تابع توزیع تجمعی دیده میشود. در محور افقی مقدارهای متغیر تصادفی و در محور عمودی نیز مقدار احتمال تجمعی دیده میشود. خطوط خاکستری روی محور افقی، نشان دهنده مقدار مشاهده آن مقدار است. از آنجایی که ۲۰ مشاهده وجود دارد، احتمال هر یک از آنها برابر با یعنی 0.05 است. بنابراین ارتفاع خطوط خاکستری به اندازه 0.05 در نظر گرفته شده که احتمال مشاهده هر مقدار است.
برای رسم خطوط آبی رنگ در هر نقطه مثلا ، مجموع احتمالات (ارتفاع خطوط خاکستری) تا نقطه محاسبه میشود. در هر نقطهای از محور افقی که این مجموع تغییر نکرده است، خط آبی را به صورت افقی کشیدهایم و هرگاه تغییری وجود داشته است، خط آبی رنگ دارای یک پرش به میزان تغییر صورت گرفته، خواهد داشت.
برای مثال، مقدار تابع توزیع تجربی برای نقطه چهارم () برابر است با:
آماره کولموگروف-اسمیرنف
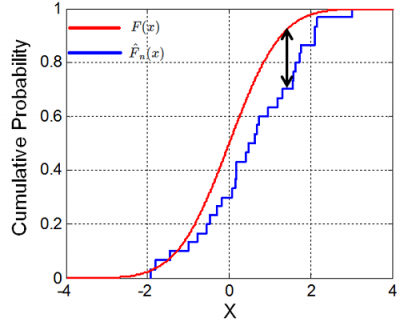
با توجه به تعریف ذکر شده برای تابع توزیع تجربی، آماره کولموگروف-اسمیرنف به صورت زیر تعریف میشود.
منظور از پیدا کردن کوچکترین کران بالا برای فاصله بین دو توزیع تجربی و توزیع واقعی روی همه مقدارها است. میتوان نشان داد که اگر مشاهدات از توزیع باشند، مقدار با افزایش مقدار به سمت صفر میل میکند.
در آزمون کولموگروف-اسمیرنف فرض صفر و فرض مقابل به صورت زیر نوشته میشود:
توزیع تجربی با توزیع اصلی یکسان است
توزیع تجربی با توزیع اصلی یکسان نیست
به این ترتیب برای تعیین ناحیه بحرانی (Critical Area) از چندک ام بالایی توزیع کولموگروف () استفاده کرده و اگر آماره آزمون یعنی بزرگتر باشد، فرض صفر (یعنی یکسان بودن توزیع تجربی با توزیع واقعی) را رد میکنیم.
رابطه ۱
نکته: آزمون کولموگروف-اسمیرنف برای آزمون کردن مطابقت با توزیع نرمال، مناسب نیست. نسخههای اصلاح شده آن از جمله آزمون لیلیفورس (Lilliefors) برای سنجش نرمال بودن دادهها بهتر عمل میکند. در ادامه به بررسی این روش خواهیم پرداخت. همچنین آزمون اندرسن-دارلینگ در این زمینه حتی با وجود دادههای کم، دارای توان آزمون بیشتری نسبت به آزمون کولموگروف-اسمیرنف است.
همانطور که قبلا گفته شد، از آزمون و آماره کولموگروف-اسمیرنف برای بررسی هم توزیعی دو متغیر تصادفی نیز میتوان استفاده کرد. فرض کنید دادههای مربوط به جامعه اول با توزیع تجربی معرفی شدهاند. همچنین دادههای جامعه دوم با توزیع تجربی مشخص شدهاند.
به این ترتیب فرض صفر و فرض مقابل برای آزمون یکسان بودن توزیع تجربی و به صورت زیر نوشته میشود.
توزیع تجربی با توزیع تجربی یکسان است
توزیع تجربی با توزیع تجربی یکسان نیست
در چنین حالتی آماره کولموگروف-اسمیرنف به صورت زیر نوشته خواهد شد.
و ناحیه بحرانی برای آن مطابق با رابطه زیر است:
رابطه ۲
البته برای محاسبه مقدار باید از روشهای عددی استفاده کرد. در جدول زیر برای بعضی از مقدارهای محاسبه صورت گرفته است.
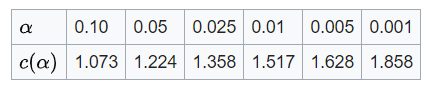
همچنین برای محاسبه تقریبی به ازاء مقدارهای دیگر مطابق با رابطه زیر عمل میشود.
نکته: همانطور که در محاسبه و اجرای آزمون کولموگروف-اسمیرنف دیده شد، احتیاج به برآورد هیچ پارامتری از دادهها نیست.
اصلاح لیلیفورس (Lilliefors) در آماره و آزمون کولموگروف-اسمیرنف
برای سنجش و مقایسه توزیع احتمال دادهها با توزیع نرمال، آزمون کولموگروف-اسمیرنف خیلی محتاط عمل میکند. به این معنی که تا حد امکان رای به نرمال بودن دادهها میدهد و خیلی به ندرت (با وجود چولگی و وجود نقاط پرت) فرض نرمال بودن را رد میکند. ولی در روش اصلاح شده «لیلیفورس» (Lilliefors)، که توسط دانشمند آمریکایی آمار و استاد دانشگاه واشنگتن «هوبرت لیلیفورس» (Hubert Lilliefors) ایجاد شده، دقت آزمون کولموگروف-اسمیرنف برای توزیع نرمال بهبود یافته است. مراحل انجام این آزمون به صورت زیر است:
- میانگین و واریانس دادهها محاسبه میشود.
- محاسبه فاصله بین توزیع تجربی و توزیع نرمال با پارامترهای برآورد شده توسط دادهها که در بخش اول بدست آمده.
- محاسبه آماره کولموگروف-اسمیرنف براساس مقادیر مشاهده شده از مرحله ۲.
از آنجایی که برآورد پارامترها برای توزیع نرمال صورت گرفته است، آماره حاصل از مرحله ۳ دیگر دارای توزیع کولموگروف نیست بلکه دارای توزیع لیلیفورس است. با توجه به نزدیکتر شدن توزیع نرمال با توجه به برآورد پارامترهای آن توسط دادهها، آماره آزمون لیلفورس نسبت به آماره کولموگروف-اسمیرنف به صورت احتمالی کوچکتر است. محاسبات مربوط به توزیع آماره لیلیفورس توسط روشهای شبیه سازی مونتکارلو صورت میگیرد.
انجام آزمون برازش توزیع کولموگروف-اسمیرنف در SPSS
فرض کنید 250 داده به عنوان یک نمونه از یک جامعه آماری در اختیار شما قرار گرفته است. میخواهیم بررسی کنیم که آیا این دادهها دارای توزیع یکنواخت در بازه هستند یا خیر. گامهای مورد نیاز برای اجرای آزمون برازش کولموگروف-اسمیرنف در SPSS به صورت زیر هستند. این دادهها با قالب فشرده برای SPSS از اینجا قابل دریافت هستند.
در نخستین گام از فهرست Analysis گزینه Nonpamateric Test را انتخاب کنید. از فهرست ظاهر شده، دستور One Sample را اجرا کنید. در پنچره ظاهر شده به نام One-Sample Nonparametric Tests در برگه Objective هدف از اجرای آزمون را با انتخاب گزینه Automatically Compare observed data to hypothesized، «اجرای خودکار آزمون فرض»، انتخاب کنید.
در برگه دوم به نام Fields نیز مشخص کنید که آزمون باید روی کدام متغیرها اجرا شود. این تنظیمات را مطابق با تصویر زیر انجام دهید.
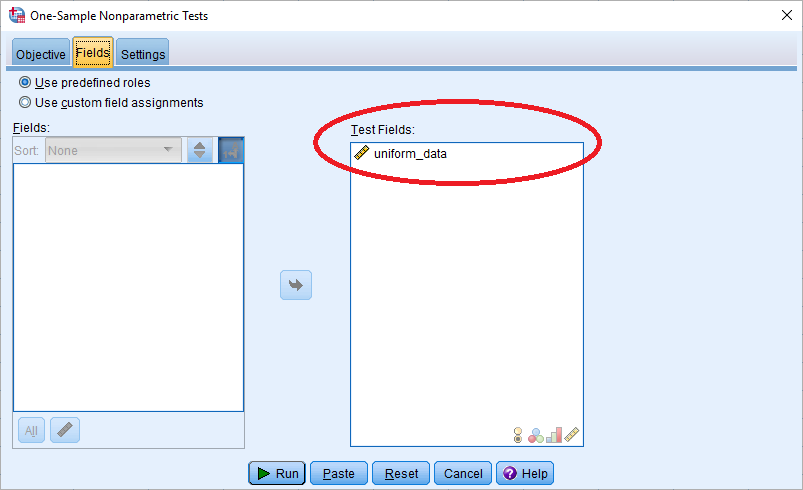
مشخص است که باید آزمون روی متغیر uniform_data اجرا شود. برای تعیین آزمون مورد نظر از این پنجره برگه Settings را انتخاب کنید تا به انواع آزمونهای ناپارامتری دسترسی پیدا کنید. در تصویر زیر انتخاب آزمون کولموگرو اسمیرنف به همراه تنظیمات مربوط به توزیع یکنواخت ظاهر شده است.
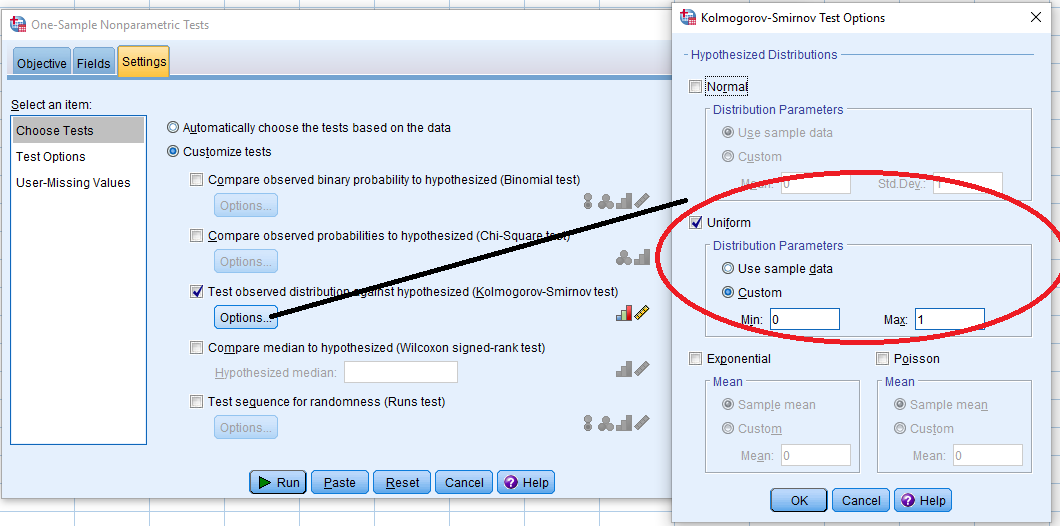
همانطور که در تصویر دیده میشود، توزیع مورد نظر برای آزمون، توزیع یکنواخت با پارامترهای 0 و 1 است. با فشردن دکمه Run پس از انجام تنظیمات، خروجی به صورت زیر درخواهد آمد.

با توجه ستون Sig در خروجی، دیده میشود که در سطح خطای 0.05، فرض صفر که در ستون Null Hypothesis یکنواخت بودن توزیع دادهها است، رد نمیشود. در ستون Decision نیز همین امر گوشزد شده است. اگر روی این خروجی دوبار کلیک کنید، پنجره «نمایش مدل» (Model Viewer) ظاهر و نمودار توزیع احتمال به همراه خلاصه آزمون نمایش داده میشود.
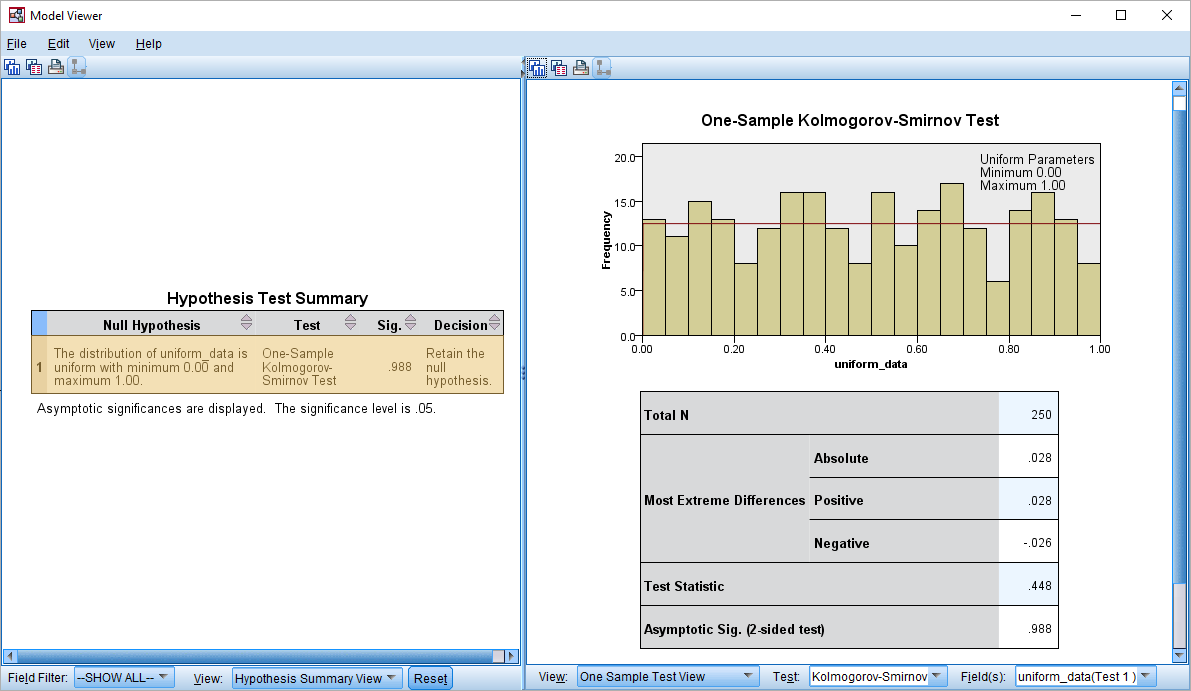
در کادر سمت راست، حداکثر قدر مطلق میزان اختلاف بین توزیع یکنواخت و توزیع تجربی دادهها برابر با 0.028 است. با توجه به رابطه محاسباتی برای آماره آزمون که در رابطه ۱ قابل مشاهده است، نتیجه برابر با 0.488 محاسبه شده. با مقایسه آن با مقدار صدک 95ام توزیع کولموگروف () فرض صفر رد نخواهد شد. بنابراین به نظر میرسد که توزیع تجربی دادهها با توزیع یکنواخت مطابقت دارد. این واقعیت را به کمک مقدار Asymptotic Sig= 0.988 (مقدار تقریبی برای مقدار Sig) نیز میتوان مشاهده کرد. از آنجایی مقدار احتمال (p-value) یا همان Sig بزرگتر از احتمال خطای نوع اول () است، فرض صفر رد نخواهد شد.
آزمون نرمال بودن دادهها در SPSS
باز هم فرض کنید یک نمونه ۲۵۰تایی دارید. میتوانید این مجموعه دادهها را که با قالب فشرده از فایل اطلاعاتی SPSS است، از اینجا بارگذاری کنید. به منظور بررسی همتوزیع بودن این دادهها با توزیع نرمال، از آزمون کولموگروف-اسمیرنف به همراه اصلاح لیلیفورس در SPSS استفاده میکنیم. فرض کنید باید نرمال بودن دادههای متغیر normrand را بررسی کنیم. از فهرست Analysis گزینه Nonparametric Tests و از فهرست ظاهر شده زیر فهرست Legacy Dialogs و دستور را انتخاب کنید.
در پنجره One-Sample Kolmogorov-Smirnov Test متغیر مربوط به آزمون را در کادر Test Variable List قرار دهید. با انتخاب توزیع نرمال (Normal) در کادر Test Distribution، توزیع مورد نظر برای فرض صفر در آزمون فرض را نرمال انتخاب کنید.
با فشردن دکمه Ok، نرمافزار SPSS خروجی را تولید کرده و آزمون را اجرا مینماید. در تصویر زیر نمونه خروجی برای دادههای مثال، نمایش داده شده است. همانطور که دیده میشود، در زیرنویس جدول اطلاعاتی مشخص شده که از آماره لیلیفورس (Lilliefors) استفاده شده است.

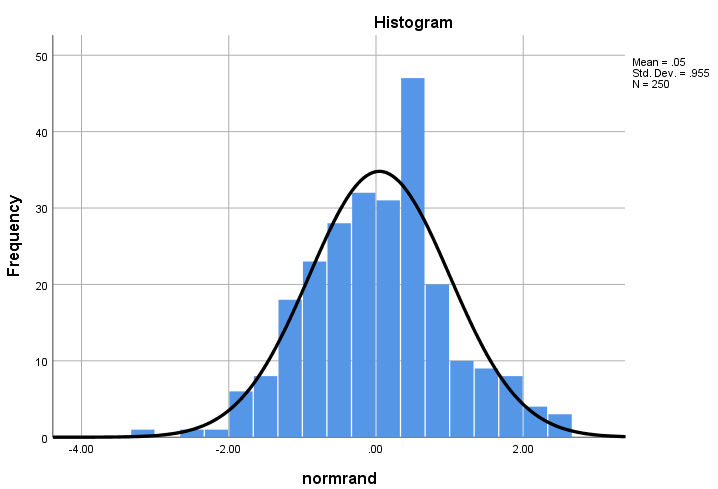
با توجه به بزرگتر بودن مقدار احتمال یا Asymp Sig= 0.088 از احتمال خطای نوع اول فرض صفر که معتبر بودن توزیع نرمال برای دادهها است، رد نمیشود. البته این فرض را به کمک نمودار فراوانی نیز میتوان نشان داد.
حال دادهها را دست کاری میکنیم. مقدارهای بزرگ و کوچک را طوری تغییر میدهیم تا نمودار بافتنگار فراوانی به صورت چوله درآید. از بین بزرگترین مقدارها، سه مقدار که بزرگترین مقادیر هستند را انتخاب کرده و با دادهها ۵، ۶ و ۷ جایگزین میکنیم. همچین سه مقداری که از همه کوچکتر هستند را با مقدار 3- تغییر میدهیم. به نمودار فراوانی دادههای تغییر یافته توجه کنید.
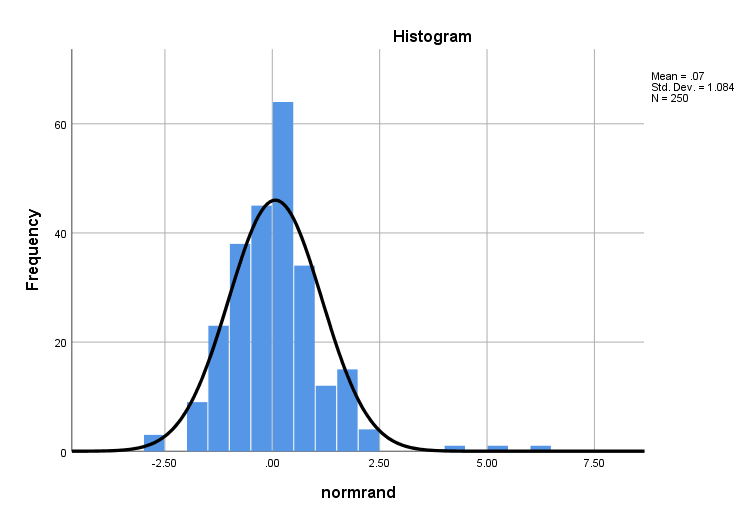
حال آزمون کولموگروف-اسمیرنف را اجرا میکنیم. همانطور که در خروجی زیر میبینید، نرمال بودن دادهها رد خواهد شد. زیرا مقدار Asymp. Sig تقریبا برابر با صفر است. در البته باید یادآور شد که آزمون صورت گرفته با توجه به میانگین و واریانس برآورد شده توسط نمونه، مربوط به نرمال بودن توزیع داده با میانگین 0.0825 با انحراف استاندارد 1.14237 است.

اگر آزمون مربوط به مقایسه توزیع دادهها با توزیع نرمال با میانگین صفر و انحراف استاندارد ۱ را اجرا کنیم، فرض صفر با توجه به آماره کولموگروف-اسمیرنف رد نخواهد شد در حالیکه چولگی کاملا در نمودار فراوانی مشهود است.
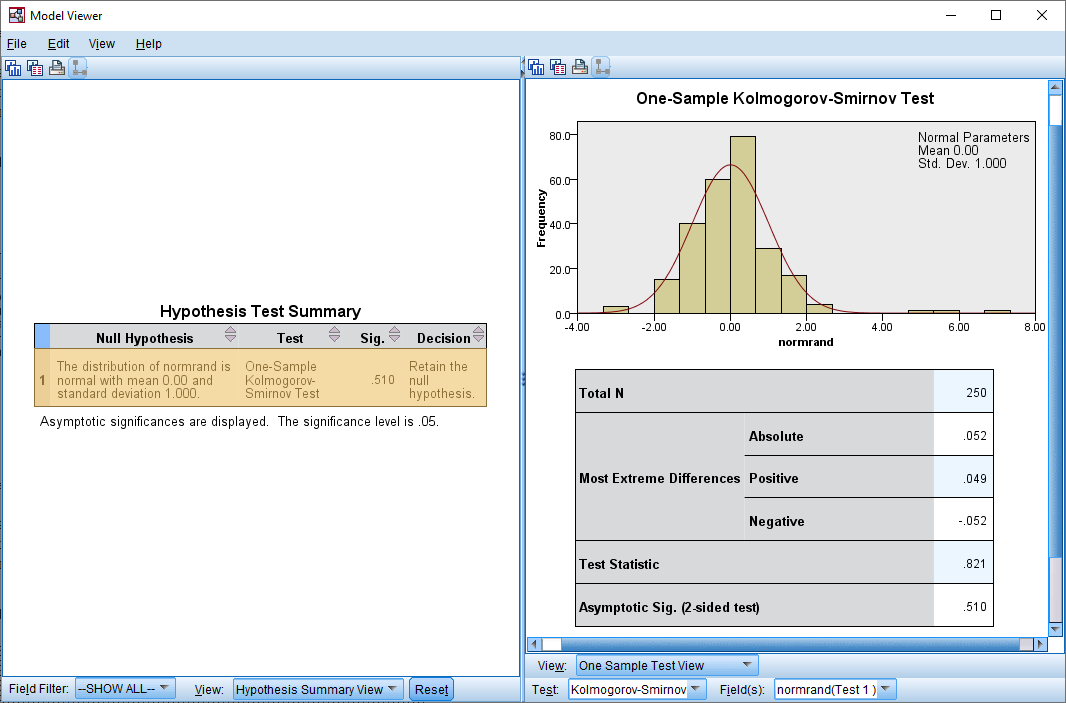
با توجه به مقدار Asymptotic Sig که برابر با 0.510 است، دلیلی برای رد فرض صفر وجود ندارد. بنابراین دیده میشود در زمانیکه حتی دادهها دارای چولگی هستند، بازهم آزمون کولموگروف -اسمیرنف رای به نرمال بودن دادهها داده است.
مطابقت توزیع احتمالی در دو جامعه آماری در SPSS
فرض کنید دو نمونه از دو جامعه در دسترس شما است. میخواهید یکسان بودن توزیع این دو جامعه را بررسی کنید. از آنجایی که در مورد پارامترها و توزیع احتمال هیچ یک از جوامع اطلاعی ندارید، از شیوه و روش آزمون کولموگروف-اسمیرنف برای مقایسه توزیع تجربی دو جامعه استفاده خواهیم کرد.
اطلاعات مربوط به نمونههای این دو جامعه در جدول زیر قابل مشاهده است. در سطرهای فرد این جدول، مقادیر و در سطرهای زوج شماره جامعهای که نمونه از آن گرفته شده است، دیده میشود.
| 0.11 | 0.09 | 0.75 | 0.87 | 0.74 | 0.03 | 0.70 | 0.06 | 0.27 | 0.03 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 0.81 | 0.74 | 0.05 | 0.74 | 0.47 | 0.47 | 0.51 | 0.01 | 0.24 | 0.49 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 2 | 2 |
| 0.18 | 0.91 | 0.90 | 0.25 | 0.31 | 0.72 | 0.39 | 0.25 | 0.18 | 1.00 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 0.56 | 0.05 | 0.11 | 0.13 | 0.28 | 0.38 | 0.53 | 0.41 | 0.29 | 0.12 |
| 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
به این ترتیب واضح است که مقدار 0.11 متعلق به جامعه اول و مثلا مقدار 0.12 (آخرین مشاهده) مربوط به جامعه دوم است. میخواهیم با توجه به متفاوت بودن تعداد اعضای هر گروه، آماره آزمون کولموگروف-اسمیرنف را محاسبه و براساس مقدار احتمال، نسبت به رد فرض صفر اقدام کنیم. گامهای زیر مربوط به انجام این آزمون در SPSS است.
- گام اول: این اطلاعات را براساس دو متغیر به نامهای Value و Group در SPSS وارد کردهایم.
- گام دوم: اجرای دستور Independent Samples از گزینه Nonparametric Test از فهرست Analysis.
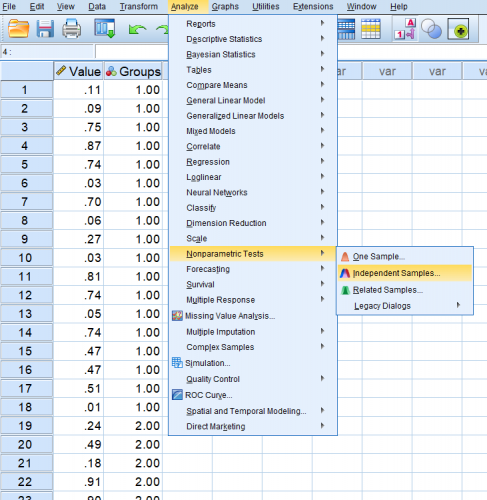
- گام سوم: تنظیمات مربوط به اجرای آزمون مطابق تصویر زیر. این تنظیمات در دو تصویر زیر قابل مشاهده هستند. تصویر اول مربوط به برگه Fields و تصویر دوم نیز مربوط به برگه Settings است.
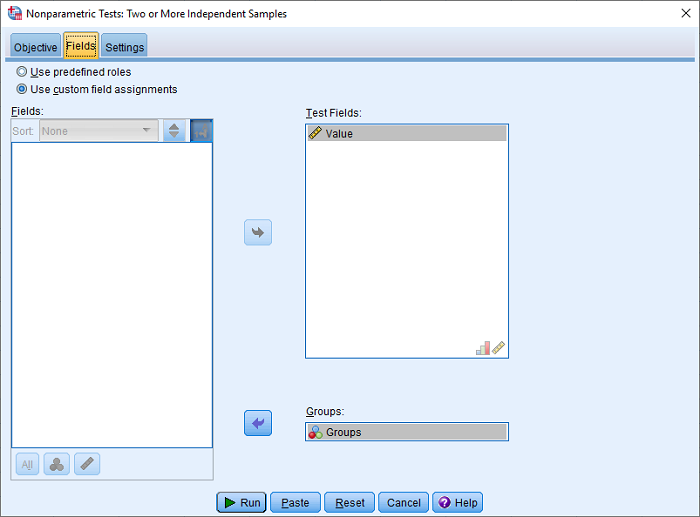
پس از انجام این تنظیمات، با فشردن دکمه Run، خروجی ظاهر خواهد شد.

همانطور که در ستون Sig مشخص است، با توجه به مقدار 0.343 فرض صفر که برابری توزیع دو جامعه است، رد نمیشود. این امر در ستون Decision نیز با ثبت عبارت Retain the null hypothesis تاکید شده است. به این ترتیب فرض صفر با توجه به نمونههای بدست آمده از جوامع 1 و ۲ تایید میگردد. با دوبار کلیک روی کادر، پنجره Model Viewer ظاهر خواهد شد.
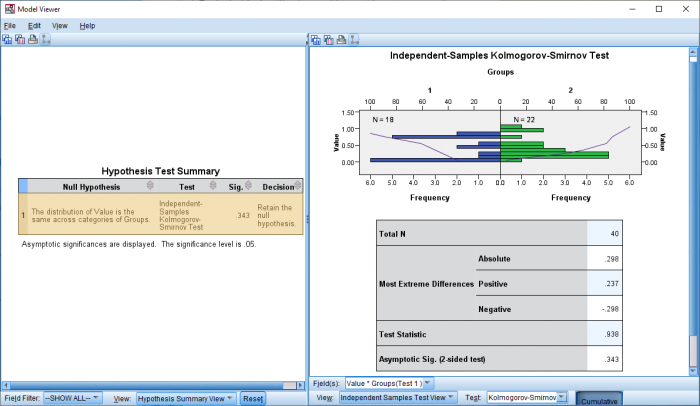
مطابق با رابطه ۲ آماره آزمون برابر است با 0.938 و مقدار احتمال نیز 0.343 است. به این ترتیب فرض صفر رد نخواهد شد. در این پنجره نمودار رسم شده، مقایسه نمودار فراوانی برای دو جامعه است. همنطور که میبینید شکل نمودار فراوانی تجمعی که به صورت یک خط برای هر دو جامعه ترسیم شده، تقریبا شبیه به یکدیگر است.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای نرمافزارهای آماری
- آموزش آمار و احتمال مهندسی
- مجموعه آموزشهای آمار احتمالات و دادهکاوی
- آزمایش تصادفی، پیشامد و تابع احتمال
- مقدار احتمال (p-Value) — معیاری ساده برای انجام آزمون فرض آماری
- توزیع نرمال یک و چند متغیره — مفاهیم و کاربردها
- توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس
^^













درود
استاد عزیز من طرح پیش ازمون پس آزمون و پیگیری با گروه کنترل دارم . با ت
برای جدا کردن گروها split انجام بدم تا نمره کنترل از آزمایش جدا شود
تشکر از فرادرس متحوای مفید را نشر میکند