انواع متغیرها در آمار | با مثال و به زبان ساده

مقادیر عددی در محاسبات ریاضی و همچنین آمار، نقش مهمی دارند. ولی در بسیاری از مواقع، باید رابطه‌ای بین این مقادیر را قبل از اندازه‌گیری آن‌ها ارائه کنیم. به این ترتیب رابطه یا فرمول مربوطه تعیین شده و پس از اندازه‌گیری کمیت‌های مورد نظر، محاسبات صورت می‌گیرد. برای اینکه بتوانیم قبل از اندازه‌گیری، برای این کمیت‌ها، از آن‌ها استفاده کنیم، لازم است که به آن‌ها اسمی بدهیم. این امر منجر به ظهور متغیرها در ریاضیات و علوم دیگر شد. معمولا متغیرها را با اسامی لاتین مثل X یا Y نشان می‌دهند. در این متن می‌خواهیم با انواع متغیرها در آمار آشنا شده و با ذکر مثال‌هایی، ماهیت آن‌ها را مشخص کنیم.

برای آشنایی بیشتر با مباحث مربوط به متغیرها بهتر است نوشتارهای معادله و نامعادله در ریاضی — پیدایش و کاربردها و جامعه آماری – انواع داده و مقیاس‌های آن‌ها را مطالعه کنید. همچنین خواندن مطالب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال و استنباط آماری | مفاهیم اولیه و روش‌ها — به زبان ساده از مجله فرادرس نیز خالی از لطف نیست.

انواع متغیرها در آمار

همانطور که گفته شد، متغیرها، بستر یا مکانی برای قرارگیری مقادیر اندازه‌گیری شده هستند. فرمول‌ها و محاسبات براساس نمادهایی که برای متغیرها به کار می‌رود، نمایش داده شده و به کار گرفته می‌شوند. برای مثال فرمول زیر برای محاسبه میانگین ۵ مشاهده مناسب خواهد بود.

$$\large \bar{X} = \dfrac{X_1 + X_2 + X_3 + X_4+ X_5}{5}$$

همانطور که می‌بینید، بخشی از فرمول (صورت کسر) با متغیرها و بخشی (مخرج) با عدد تکمیل شده است. واضح است که منظور از $$X_1$$ مقدار مشاهده اول و $$X_2$$ مقدار مشاهده دوم و الی آخر است. ولی از آنجایی که هنوز اندازه‌ای مشخص نشده برای نمایش این مقادیر از اسامی متغیرها استفاده شده است.

شاید بتوان فرمول بالا را به صورت زیر به بیان نوشتاری درآوریم.

مقدار اول را با مقدار دوم، سپس با مقدار سوم و چهارم و پنجم جمع و حاصل را بر ۵ تقسیم کن.

به این ترتیب یک عبارت فارسی طولانی به یک عبارت ریاضی ساده و کوتاه درآمد. این هنر استفاده از انواع متغیرها در آمار و فرمول‌های مربوطه محسوب می‌شود.

اینکه چه مقادیری در این متغیرها قرار می‌گیرند، باعث طبقه‌بندی متغیرها می‌شود. از این جهت می‌توان انواع متغیرها در آمار را به صورت زیر تفکیک کرد.

• متغیرها با مقادیر کیفی
• متغیرها با مقادیر کمی

از یک نظر ممکن است انواع متغیرها در آمار را براساس مجموعه اعدادی که می‌پذیرند، طبقه بندی کنند. برای مثال اگر دامنه تغییرات مقادیر عددی، فقط «مجموعه اعداد صحیح» شامل مقادیر مثبت یا منفی (Whole Numbers) باشند، آن را «متغیرهای گسسته» (Discreet Variable) می‌نامند. از طرفی اگر مجموعه مقادیر آن‌ها، همراه با اعشار بوده و شامل «اعداد حقیقی» (Real Numbers) باشد، متغیر را «پیوسته» (Continuous) نام‌گذاری می‌کنند.

از جنبه دیگر نقش هر متغیر در تحلیل و ایجاد مدل آماری نیز تعیین کننده است. برای مثال در مدل‌های رگرسیونی، یک متغیر نقش پیش‌گو یا «مستقل» (Independent) و متغیر دیگر به عنوان متغیر «وابسته» (Dependent) نامیده می‌شوند. همانطور که خواهید دید، در بین انواع متغیرها در آمار بخصوص در مدل سازی انواع دیگری مانند متغیرهای کنترل و متغیر پنهان نیز نقش داشته و متغیرها را دسته‌بندی می‌کنند.

در این راستا می‌توان متغیرها را به چهار دسته مختلف تعیین کرد.

• متغیر مستقل
• متغیر وابسته
• متغیر کنترل
• متغیر پنهان

در ادامه این طبقه‌بندی‌ها را با ذکر مثال‌هایی، بیشتر توضیح می‌دهیم.

دسته بندی متغیرها از لحاظ نوع مقادیر

همانطور که گفته شد، اگر مقادیر متغیرها را برای دسته‌بندی ملاک قرار دهیم، می‌توانیم انواع متغیرها در آمار را به دو دسته کیفی و کمی تفکیک کنیم. در ادامه هر یک از این دو نوع را با ذکر مثال‌هایی معرفی کرده و شما را با آن‌ها بیشتر آشنا خواهیم کرد.

فیلم آموزش مقدماتی روش تحقیق کیفی در فرادرس

کلیک کنید

متغیرها با مقادیر کیفی

به مقدارهایی که از مشاهده یا سنجش کیفیت بدست می‌آیند، مقادیر یا داده‌های کیفی می‌گویند. این نوع داده‌ها، اغلب در رابطه با صفت یا ویژگی‌های افراد یا پدیده‌های مورد بررسی، در نظر گرفته می‌شوند. در اکثر موارد از مقادیر کیفی برای «افراز» (Partition) یا «تفکیک» (Segmentation) جامعه آماری استفاده می‌شود.

اندازه‌هایی مانند «محل تولد»، «گروه خون»، «رنگ چشم»، از انواع داده‌های کیفی هستند. واضح است که متغیرهایی که چنین مقادیری را به خود می‌گیرند، «متغیرهای کیفی» (Qualitative Variable) نامیده شوند. در اغلب موارد به جای استفاده از متغیر کیفی، از واژه ویژگی یا صفت (Attribute) استفاده کمک می‌گیریم.

واضح است که مقدار هر یک از ویژگی‌های کیفی با توجه به سلیقه تغییر می‌کند. برای مثال نرمی پارچه ممکن است از دید یک نفر مقداری برابر زبری داشته باشد ولی نظر فردی دیگر نرم محسوب شود. واضح است که عدم ارائه این مقادیر به صورت عددی ممکن است مشکلاتی را برای تحلیل آماری فراهم کند. برای مثال احتمالا، امکان مرتب سازی (از کوچک به بزرگ) برای مقادیر کیفی به مانند اعداد وجود ندارد. برای مثال نمی‌توان گروه خونی یا محل تولد افراد حتی رنگ چشم را به ترتیب، قرار داد.

توجه داشته باشید که ویژگی‌های کیفی و انواع داده‌های آن به صورت یک عبارت متنی مشخص می‌شوند ولی اغلب برای اجرای تحلیل‌های آماری باید براساس مقیاس مناسب، آن‌ها را بصورت عددی نمایش دهیم. این موضوع با عنوان مقیاس یا سطوح سنجش در مطلب دیگری از مجله فرادرس مورد بررسی قرار خواهد گرفت.

متغیرها با مقادیر کمی

مقادیر کمی معمولا از طریق شمارش یا سنجش با ابزارها علمی، اندازه‌گیری می‌شوند. این نوع داده‌ها، کاملا بوسیله اعداد قابل نمایش یا ارائه هستند. بزرگی و کوچکی، ترتیب و مرتب‌سازی این نوع داده‌ها بوسیله اعداد قابل تعیین است. به طور مثال طول،‌ وزن، فشار، دما و … از گروه متغیرها کمی هستند.

از آنجایی این نوع داده‌ها به صورت عددی بیان می‌شوند، امکان انجام محاسبات ریاضی روی آن‌ها وجود دارد. پس می‌توان میانگین، واریانس و دیگر شاخص‌های آماری را از روی آن‌ها محاسبه کرد. در بیشتر مواقع متغیرهای مربوط به جامعه آماری از نوع کمی هستند.

دسته بندی متغیرها از نظر نوع مقادیر عددی

اگر داده‌ها به صورت عددی باشند، معمولا آن‌ها را به دو گروه مقادیر پیوسته و گسسته طبقه‌بندی می‌کنند. این نوع گروه بندی برای تشخیص یا تعیین روش‌های آماری در یک تحقیق علمی مناسب لازم است.

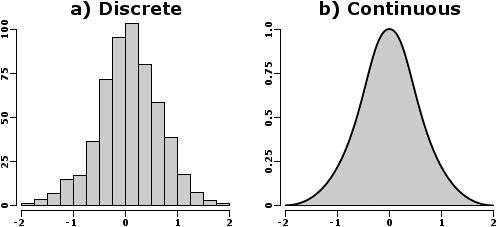
متغیرها با مقادیر پیوسته

در اکثر مواقع، ابزارهای اندازه‌گیری، دقت‌های مختلفی دارند. یک ترازو ممکن است، وزن را در حد گرم نمایش دهد و ترازوی دیگر با صدم گرم وزن را بسنجد. در این حالت، نمایش اعداد و مقادیر مربوط به متغیر، به صورت اعشاری است. برای مثال وزن را می‌توان به صورت‌های مختلف زیر نمایش داد.

$$\large W = 1.43, \;\;\; W = 14.3 ,\;\;\;\; W = 0.00143$$

تعداد ارقام (صحیح یا اعشار) می‌تواند به منزله دقت اندازه‌گیری دستگاه تلقی شده و «مقدار گرد شده» (Round) وزن را نمایش دهد. از آنجایی که این مقادیر، شامل اعضای مجموعه اعداد حقیقی هستند، آن‌ها را «پیوسته» (Continues) یا «حقیقی» (Real) می‌نامیم.

نکته: به یاد دارید که مجموعه اعداد حقیقی، شامل مقادیر مثبت، منفی، اعشاری، رادیکالی و ... هستند.

متغیرها با مقادیر گسسته

جنبه دیگر از متغیرها با مقادیر عددی، شامل اندازه‌هایی است که از طریق شمارش بدست می‌آیند. برای مثال اگر تعداد فرزندان خانوار، متغیر مورد نظر ما باشد، داده‌های حاصل فقط شامل اعداد مثبت و صفر  خواهند بود. به این ترتیب مشخص است که مقادیر کسری یا اعشاری در این متغیر، جایگاهی ندارند. چنین متغیرهایی را با نام مقادیر «گسسته» (Discrete) می‌شناسیم.

نکته: همانطور که گفته شد، متغیرهای گسسته شامل مقادیر مربوط به اعضای مجموعه اعداد صحیح (یا طبیعی) هستند.

معمولا چنین داده‌هایی نیازی به گرد کردن ندارند و به همان شکل شمارشی یا تجمیعی از شمارش‌ها در طرح‌های تحقیق با انواع متغیرها در آمار به کار می‌روند.

دسته بندی متغیرها از لحاظ ساختار مدل آماری

در یک مدل آماری، رابطه بین متغیرها سنجیده شده و به شکل یک رابطه ریاضی نوشته می‌شود. البته از آنجایی که عامل تصادف نیز در اندازه‌گیری‌ها دخیل است، مدل به همراه یک عبارت خطا (متغیر تصادفی- Random Variable) که توزیع خاص آماری دارد، به کار می‌رود. طبقه بندی که برای انواع متغیرها در آمار و مدل‌سازی ایجاد می‌شود با توجه به نقش آن‌ها در بیان رابطه مشخص می‌شود. به این ترتیب می‌توان یک متغیر را در بخش متغیرهای مستقل، وابسته، کنترل یا پنهان قرار داد. در ادامه این دسته‌بندی را بیشتر تشریح می‌کنیم.

متغیرهای مستقل و وابسته

«متغیرهای مستقل» (Independent Variables)، ویژگی‌هایی از جامعه آماری را شامل می‌شوند که قابل کنترل توسط محقق هستند یا در مدل مورد بررسی، به عنوان متغیر پیشگو به کار می‌روند. به این معنی که مقادیر آن‌ها را می‌توان از طریق نمونه‌گیری یا دسته‌بندی، تعیین نمود. برای مثال میزان مطالعه درس ریاضی یک متغیر مستقل در مسئله مدل سازی نمره ریاضی محسوب می‌شود. به این ترتیب می‌توانیم دانشجویان را وادار کنیم که در این تحقیق، بیشتر از ۲ ساعت مطالعه برای امتحان داشته باشند. حتما متوجه هستید که نمره ریاضی آن‌ها نمی‌تواند توسط محقق کنترل یا تعیین شود.

در مدل‌سازی رگرسیونی به منظور تشخیص قیمت خانه برحسب، متغیرهای مساحت زیربنا، سن بنا و تعداد اتاق خواب، متغیرهای مستقل قابل کنترل نیستند ولی می‌دانیم که در مدل ارائه شده، قیمت خانه را می‌توان وابسته به مساحت زیربنا و سن بنا و ...  دانست. به این منظور برای برآورد قیمت خانه از آن‌ها استفاده می‌کنیم.

فیلم آموزش شبیه سازی متغیرهای تصادفی و وابسته در متلب در فرادرس

کلیک کنید

در مقابل متغیرهای مستقل (پیشگو)، «متغیرهای وابسته» (Dependent Variables) قرار دارند. معمولا مقادیر مربوط به متغیرهای وابسته، علاوه بر متغیرها مستقل، با یک متغیر تصادفی نیز در رابطه است.

متغیرهای وابسته و مستقل، متغیرهایی در مدل سازی ریاضی، مدل سازی آماری و علوم تجربی محسوب می‌شوند. در یک آزمایش، مقادیر متغیرهای وابسته تحت فرض یا فرضیه‌ای مورد نظر محقق قرار می‌گیرد. چنین متغیرهایی براساس برخی قانون یا قاعده (مثلاً توسط یک تابع ریاضی) به مقادیر سایر متغیرها (متغیرها مستقل) مرتبط هستند. متغیرهای مستقل، به نوبه خود، در دامنه آزمایش مورد نظر به متغیرهای دیگری وابسته نیستند. برخی از متغیرهای متداول مستقل عبارتند از: زمان، فضا، چگالی، جرم و میزان جریان سیال ولی در عوض مقادیر مانند میزان تولید، اندازه یا رشد جمعیت انسانی و غیره متغیرهای وابسته هستند که برای پیش بینی مقادیر آینده ‌آن‌ها از متغیرهای مستقل استفاده می‌شود.

از این دو، همیشه متغیری وابسته‌ است که تنوع و پراکندگی آن با تغییر ورودی‌ها، دگرگون می‌شود. در یک آزمایش آماری، هر متغیری را که آزمایشگر و محقق قادر به دستکاری یا تعیین سطوح آن است را می‌توان یک متغیر مستقل نامید. توجه داشته باشید که مدل‌ها و آزمایش‌ها، تأثیراتی را که متغیرهای مستقل بر متغیرهای وابسته دارند، نمایش می‌دهند.

یکی دیگر از انواع متغیرها در آمار که در بعضی از مسائل و بررسی‌ها به کار می‌رود، متغیر کنترل و متغیر پنهان است که در قسمت بعدی معرفی خواهند شد.

متغیرهای کنترل

یک متغیر کنترلی (یا ثابت) در آزمایشات علمی، عنصری تجربی است که در طول تحقیق ثابت و بدون تغییر است. اگر در طول آزمایش متغیرهای کنترلی ثابت نمانند، می‌توانند نتایج آزمایشی را به شدت تحت تأثیر قرار دهند. از این جهت متغیر وابسته به متغیرهای کنترلی نیز ارتباط پیدا می‌کند. ولی باید توجه داشت که نظر محقق در انجام تحلیل و آنالیز، حذف اثر متغیرهای کنترلی است. به این منظور روش‌هایی در آمار وجود دارد که تغییرات متغیرهای کنترلی را از مدل حذف می‌کند.

برای مثال فرض کنید، در یک طرح تحقیقی، اثر یک دارو بر بیماران مورد بررسی قرار گرفته است. ولی می‌دانیم که متغیر سن در بیماران و طرح تحلیل ما، یک متغیر کنترلی است که نمی‌خواهیم در مدل به عنوان متغیر مستقل در نظر گرفته شود. در حقیقت می‌خواهیم نشان دهیم که این دارو روی همه رده‌های سنی موثر است. ولی مشخص است که سن به عنوان یک متغیر، در بهبود بیماری با دارو موثر بوده که منظور تحقیق ما نیست. بنابراین با اندازه‌گیری متغیر سن، و لحاظ کردن آن به عنوان یک متغیر کنترل، اثر آن را بر متغیر وابسته (اثر دارو) ثابت نگه داشته‌ایم. به این ترتیب می‌توانیم متغیر کنترلی را به صورت زیر تعریف کنیم.

متغیر کنترل، متغیری است که در آزمایشی، به منظور ارزیابی رابطه بین متغیرهای متعدد، اثر آن ثابت نگه داشته می‌شود.

یکی دیگر از انواع متغیرها در آمار که بخصوص در رشته‌های علوم انسانی به وفور به کار می‌رود، متغیرهای پنهان است. در ادامه چنین متغیری را مشخص خواهیم کرد.

متغیرهای قابل مشاهده و پنهان

«متغیرهای نهفته» (Latent Variables) یا پنهان، در مقابل متغیرهای قابل مشاهده قرار می‌گیرند. متغیرهای قابل مشاهد، قابل اندازه‌گیری و مشاهده هستند ولی متغیرهای پنهان، مستقیماً مشاهده نمی‌شوند اما از طریق متغیرهای دیگر قابل تعیین بوده و در مدل‌های آماری قابل استفاده هستند.

مدل‌های ریاضی و آماری که هدف آنها تبیین رابطه بین متغیرهای مشاهده شده و متغیرهای نهفته است، «مدل‌های متغیر پنهان» (Latent Variable Model) نامیده می‌شوند. مدل‌های متغیر نهفته یا پنهان، در بسیاری از رشته‌ها از جمله روانشناسی، جمعیت شناسی، اقتصاد، مهندسی، پزشکی، فیزیک، یادگیری ماشین/هوش مصنوعی، بیوانفورماتیک، شیمی، پردازش زبان طبیعی، اقتصاد سنجی، مدیریت و علوم اجتماعی مورد استفاده قرار می‌گیرند.

همچنین گاهی به منظور کاهش ابعاد یک مسئله مدل‌سازی از متغیرهای پنهان بهره می‌بریم. در مدل‌های رگرسیونی یا تحلیل عاملی، بسیاری از متغیرهای مشاهده شده را می‌توان در یک مدل جمع آوری کرد تا یک مفهوم اساسی را نشان دهند. این امر به درک داده‌ها و مدل، کمک شایانی می‌کند.

برای مثال فرض کنید، ارزیابی یک رستوران از نظر مشتریان با چندین متغیر مورد بررسی قرار می‌گیرد. مثلا متغیرهای زیر را در نظر بگیرید.

• مزه غذا
• تازگی مواد به کار رفته
• شوری و تندی
• زمان انتظار برای غذا
• گرمای مناسب
• چیدمان میز برای سرو غذا

مشخص است که متغیرهای اول تا سوم به مواد غذایی و نوع غذا ارتباط دارند که در نتیجه از طریق مشاهده این متغیرها می‌توان متغیر جدیدی به نام خصوصیات غذای سفارش داده شده، ایجاد کرد. از طرفی زمان انتظار، گرمای مناسب و چیدمان میز به ویژگی‌های مربوط به سرو غذا اختصاص دارند که به طور جداگانه قابل اندازه‌گیری نیست. به این ترتیب از ترکیب این شش متغیر، دو متغیر جدید به نام ویژگی غذا و امتیاز سرویس ساخته می‌شود. واضح است که این دو متغیر می‌توانند جایگزین همه آن‌ متغیرها بوده و به این ترتیب ابعاد مسئله کاهش خواهد یافت. توجه داشته باشید که این دو متغیر کمترین وابستگی را با یکدیگر نیز دارند.

خلاصه و جمع‌بندی

همانطور که در این مطلب از مجله فرادرس خواندید، متغیرها نقش مهمی در تعیین و نمایش رابطه‌ها در علوم مختلف (بخصوص ریاضی و آمار) دارند. طبقه یا دسته‌بندی کردن آن‌ها، به شناخت بهترشان کمک می‌کند. در این مطلب انواع متغیرها در آمار را از جنبه‌های مختلف مانند نوع مقادیر و همچنین نقش در مدل‌های آماری بازگو کردیم. البته براساس اینکه چه مقیاسی برای تبدیل داده‌ها به اعداد به کار می‌رود می‌توان سطوح سنجش را هم به عنوان دسته‌بندی به کار برد. این موضوع در نوشتار دیگری از مجله فرادرس، مورد بررسی قرار خواهد گرفت.