رسم نمودار در متمتیکا — راهنمای سریع و کاربردی

رسم نمودار توابعی که به صورت نمادین تعریف شده‌اند، کار مشکلی است. معمولا این کار به وسیله نقطه‌گذاری و محاسبه مقدار تابع صورت می‌گیرد. یکی از نرم‌افزارهای مناسب برای رسم نمودارهای ریاضی، نرم‌افزار «متمتیکا» (Mathematica) است. در این نرم‌افزار کافی است تابع مورد نظر خود را معرفی کرده و آن را با یک دستور، ترسیم کنید. بنابراین به سرعت و سادگی می‌توانیم نمودار توابع ریاضی (دو و سه بعدی) را در این نرم‌افزار ترسیم کنیم. به همین علت این نوشتار از مجله فرادرس را به آموزش رسم نمودار در متمتیکا اختصاص داده‌ایم. در ضمن به معرفی یک از آموزش‌های فرادرس که مرتبط با نرم‌افزار متمتیکا است، نیز خواهیم پرداخت.

به منظور آشنایی با نرم‌افزار متمتیکا و انواع نمودارها، بهتر است دیگر نوشتارهای مجله فرادرس با نام‌های متمتیکا (Mathematica) چیست؟ — راهنمای شروع به کار و رسم تابع — با مثال های حل شده را مطالعه کنید. همچنین خواندن رسم نمودار برای داده‌ها — معرفی و کاربردها و کاربرد انواع نمودارها و گراف‌ ها در اکسل نیز خالی از لطف نیست.

رسم نمودار در متمتیکا

در اکثر نرم‌افزارهای محاسبات ریاضی و عددی، امکان ترسیم نمودار براساس مشخص کردن نقاط، میسر است. ولی چیزی که در نحوه رسم نمودار در متمتیکا متمایز است، معرفی تابع به صورت نمادین و در عین حال ترسیم آن بدون معرفی زوج نقاط برای رسم است. به همین دلیل، رسم نمودار در متمتیکا لذتی دارد که با هیچ نرم‌افزار دیگری قابل مقایسه نیست. از طرفی سرعت و ویژگی‌های خاص این نرم‌افزار، ترسیم نمودارهای پیچیده را میسر کرده و تصاویر زیبایی از توابع ریاضی و به طور کلی، موضوعات حوزه ریاضیات ارائه می‌دهد.

فیلم آموزش محاسبات عددی با متمتیکا Mathematica – مقدماتی در فرادرس

کلیک کنید

اطلاع دارید که کد نویسی در متمتیکا به زبان «ولفرام» (Wolfram) صورت می‌گیرد. در این زبان، کدها و دستورات متعددی برای ترسیم توابع و داده‌ها وجود دارد. گزینه‌های متعددی نیز به عنوان تنظیمات (Options) برای زیبا سازی یا ایجاد جزئیات بیشتر در نمودار قابل استفاده است. به این ترتیب نموداری که حاصل می‌شود، کاملا مطابق با نظر و دیدگاه کاربر خواهد بود.

فرمان رسم نمودار در متمتیکا

رسم نمودار در متمتیکا با دستورات مختلفی قابل انجام است. در ادامه لیستی از این دستورات و تصاویری از نمودارهای رسم شده را مشاهده می‌کنید. البته هر یک از این دستورات، شکل خاصی از نمودار (مثلا دو بعُدی یا سه بُعدی- خطی یا نقطه‌ای) را ترسیم می‌کنند.

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

دستور Plot و رسم نمودار برای توابع ریاضی

اغلب موارد برای رسم یک تابع از دستور Plot بهره می‌گیریم. در تصویر ۱، نمونه‌ای از نمودار «تابع سینوس» (Sin)‌ را مشاهده می‌کنید. کد لازم برای ترسیم این نمودار با استفاده از دستور Plot در زیر مشخص شده است.

1Plot[Sin[x], {x, 0, 10}]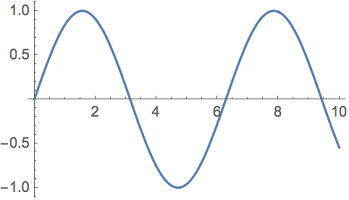

همانطور که در کد مشاهده می‌کنید، بخش اول یا پارامتر اول تابع Plot به معرفی تابع ریاضی پرداخته است. در بخش دوم نیز متغیر و محدود تغییرات آن مشخص شده است. به این ترتیب تابع سینوس برای مقادیر از محور افقی ترسیم می‌شود که در بازه $$[0,10]$$ قرار گرفته‌اند. البته توجه داشته باشید که واحد اندازه‌گیری زاویه (مقادیر محور افقی) هنگام رسم نمودار در متمتیکا بر حسب رادیان هستند.

از طرفی واضح است که مقادیر روی محور عمودی نیز در بازه ۱- تا ۱ قرار خواهند داشت. به این ترتیب برای زاویه‌ای با مقدار ۳٫۱۴ که همان مقدار عدد پی (یا یک رادیان) است، مقدار سینوس برابر با صفر شده است. همه ضرایب صحیح از ۳٫۱۴ یا عدد پی نیز دارای مقدار سینوس صفر هستند. از طرفی نصف این مقدار یعنی $$\pi /2$$ و همه ضرایب فرد آن، مقدار سینوسی برابر با 1 یا ۱- خواهند بود.

دستور ListPlot و رسم نمودار نقطه‌ای برای داده‌های زوجی

برای رسم نقاط روی مختصات دکارتی از دستور ListPlot استفاده می‌شود. شکل دستوری به صورت ساده (با کمترین پارامتر) برای این فرمان، به صورت زیر است. توجه داشته باشید که تنها پارامتر الزامی برای دستور ListPlot، ذکر مجموعه داده‌ای است که شامل زوج‌های مرتب $$(x,y)$$ هستند. اولین مولفه به عنوان مقادیر محور افقی و دومین مولفه در این مجموعه داده، برای مقادیر محور عمودی به کار می‌رود.

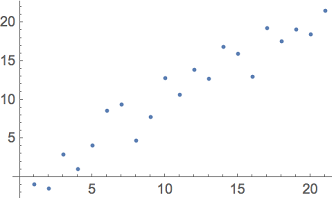
به نموداری که در تصویر ۲ قابل مشاهده است، توجه کنید. این نمودار به صورت نقطه‌ای (Dotplot) رسم شده و دارای دو محور افقی و عمودی است. دستور لازم برای رسم چنین نموداری در زیر دیده می‌شود.

1datapts = Table[x + RandomReal[{-4, 4}], {x, 0, 20}];
2ListPlot[datapts]

همانطور که مشخص است، ابتدا یک مجموعه داده با ساختار جدولی (Table) از مقادیر ۰ تا ۲۰ برای محور افقی (مقادیر x) و مجموع آن‌ها با یک عدد تصادفی در بازه ۴- تا ۴، برای محور عمودی (مقادیر تابع یا y) در نظر گرفته شده. نام این مجموعه داده، datapts انتخاب شده است. بنابراین کافی است به سادگی، این نام را به عنوان پارامتر دستور ListPlot تعیین کنیم، تا نموداری مطابق با تصویر ۲ ظاهر شود.

نکته: اگر بخواهید نقاط ترسیم شده در نمودار قبلی را به یکدیگر متصل کنید و به صورت خطوط شکسته، نمایش دهید، کافی است از دستور ListLinePlot استفاده کنید. کد مربوطه به صورت زیر خواهد بود. واضح است که پارامترهای ضروری برای ترسیم این نمودار، دقیقا با دستور ListPlot مشابهت دارد.

1ListLinePlot[datapts]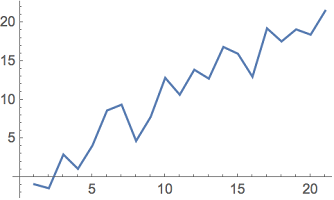

این بار با استفاده از دستور Show، دو نمودار، یعنی نمودار اصلی (مطابق با تصویر ۲) و نمودار بهترین برازش چندجمله‌ای را برای یک مجموعه داده‌ ترسیم کنیم. این مقادیر به صورت زوج مرتب‌هایی به صورت زیر هستند.

$$\large  (1,2) , (2,3), (3,5), (4,7) , (5,11) , (6 , 13)$$

نکته: از آنجایی که مقادیر مولفه اول (محور افقی) دارای ترتیب هستند و با یک واحد مشخص شده‌اند، می‌توانید در کد از آن‌ها چشم‌پوشی کرده و فقط مقادیر محور عمودی را مشخص کنید.

به این ترتیب اگر یک چند جمله‌ای درجه ۲، با مقدار ثابت (توان صفر x) معرفی کنیم، معادله بهترین برازش منحنی مطابق با کد زیر حاصل خواهد شد.

1Fit[{2, 3, 5, 7, 11, 13}, {1, x, x^2}, x]

نتیجه یک تابع چند جمله‌ای با ضرایب برآورد شده به صورت زیر است.

$$\large y = 0.9 + 0.689286x + 0.232143 x^2$$

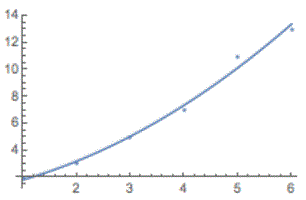
حال این تابع را در کنار منحنی مربوط به نمودار ترسیم شده از نقاط (نمودار نقطه‌ای) رسم خواهیم کرد.

1Show[{Plot[%, {x, 1, 6}], ListPlot[{2, 3, 5, 7, 11, 13}]}]

همانطور که مشاهده می‌کنید با استفاده از دستور Show، دو نمودار روی یکدیگر در یک مختصات ترسیم شده‌اند. نمودار اول بوسیله تابع Plot کشیده شده و مربوط به نمایش منحنی برازش شده است. علامت ٪ نشانگر آخرین خروجی است که برای رسم نمودار آن در بازه ۱ تا ۶ استفاده شده. دستور ListpPlot‌ نیز نمودار نقطه‌ای را برای زوج‌های مرتب ترسیم کرده است و نتیجه مطابق با تصویر ۴ است.

دستور Plot3D و رسم نمودار سه بُعدی برای توابع ریاضی

اگر با تابعی دو متغیره سروکار دارید و می‌خواهید تغییرات آن را برحسب دو مولفه بسنجید، رسم نمودار سه بُعدی می‌تواند یک راهکار مناسب باشد. برای توابع دو متغیره (نمودار سه بُعدی) رسم نمودار در متمتیکا با دستور Plot3D صورت می‌گیرد. فرض کنید بخواهیم تابع دو متغیره زیر را رسم کنیم.

$$\large \displaystyle {z = f(x,y)  = \sin(x) \cdot \cos(y)}$$

البته در نظر داشته باشید که باید برای مقادیر محورهای x و y یک محدوده در نظر بگیریم. دستور Plot3D را به صورت زیر برای ترسیم تابع بالا، به کار می‌بریم.

1Plot3D[Sin[x] Cos[y], {x, 0, 5}, {y, 1, 10}]

همانطور که می‌بینید، بازه برای محور x، فاصله $$(0,5)$$ و برای محور y، بازه $$(2,10)$$ در نظر گرفته شده و حاصل‌ضرب سینوس x در کسینوس y‌ به عنوان مقدار تابع،‌ مورد محاسبه قرار گرفته است. نتیجه رسم این تابع در مختصات دکارتی سه بُعدی به مانند تصویر ۵ خواهد بود.

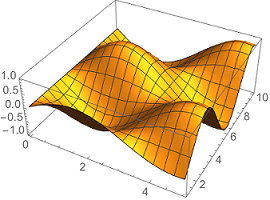
توجه داشته باشید که محورهای پایینی (طول و عرض) که به صورت پرسپتکتیو ظاهر شده‌اند، مربوط به مقادیر x و y‌ هستند و نموداری که ارتفاع را نشان می‌دهد، مقدار تابع دو متغیره را بیان می‌کند.

دستور GraphPlot و رسم نمودار شبکه (Network)

خوشبختانه، رسم نمودار شبکه (Network) یا گراف (Graph) در متمتیکا به سادگی صورت می‌گیرد. کافی است از دستور GraphPlot استفاده کرده و ارتباط بین گره‌ها (Nodes) را با علامت → مشخص کنید. به دستور زیر توجه کنید.

1GraphPlot[{1 -> 2, 1 -> 4, 2 -> 4, 3 -> 4, 3 -> 2, 3 -> 5, 5 -> 1}, 
2 VertexLabeling -> True]

همانطور که دیده می‌شود،‌ گره ۱ به ۲ و ۴ متصل است. گره ۲ نیز به گره ۴ و گره ۳ نیز با گره ۴ و ۲ ارتباط دارد. گره ۳ نیز با گره‌های ۲ و ۵ مرتبط بوده و گره ۵ فقط به گره ۱ ارتباط دارد. پارامتر دوم یعنی VertexLabeling به نمایش برچسب گره‌ها در نمودار اشاره دارد. از آنجایی که مقدار True برای این پارامتر در نظر گرفته شده، برچسب اسامی گره‌ها در نمودار ظاهر خواهد شد. به تصویر ۶ توجه کنید.

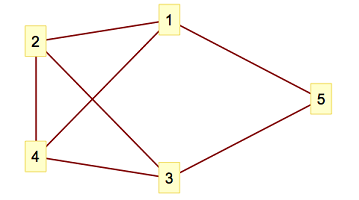
اگر بخواهیم جهت‌های تعریف شده در شبکه (جهت اتصال گره‌ها به یکدیگر) نیز در نمودار ظاهر شود، از گزینه DirectedEdges برای دستور GraphPlot استفاده خواهیم کرد. کافی است مقدار این پارامتر را برابر با True انتخاب کنید.

فیلم آموزش محاسبات عددی با متمتیکا Mathematica – تکمیلی در فرادرس

کلیک کنید

به این ترتیب با اجرای دستور زیر، نموداری مطابق با تصویر ۷ ظاهر خواهد شد. به معرفی گره‌ها و جهت آن‌ها در این دستور توجه کنید.

1GraphPlot[{1 -> 2, 2 -> 3, 3 -> 4, 4 -> 1, 2 -> 4, 4 -> 5, 4 -> 6}, 
2 DirectedEdges -> True]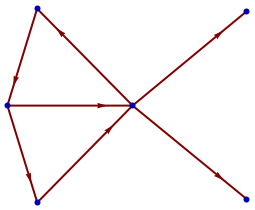

با این کد به سادگی و راحتی می‌توان گراف، درخت‌ و جنگل و موضوعات مربوط به نظریه گراف را ترسیم و نمایش داد.

خلاصه و جمع‌بندی

در این نوشتار از مجله فرادرس با نحوه ترسیم نمودار در متمتیکا آشنا شدید. به این ترتیب توابعی که به صورت نمادین در این نرم‌افزار نوشته می‌شود را می‌توان به صورت یک نمودار، نمایش داد. رسم نمودارها در مختصات دو بُعدی (2D) و سه بُعدی (3D) نیز در این متن مورد توجه قرار گرفته و دستورات لازم بازگو شد. به کمک متمتیکا حتی می‌توانید نمودارهای مربوط به گراف و شبکه‌ها را هم ترسیم کرده و ارتباط بین گره‌ها را نمایش دهید. توجه داشته باشید که نرم افزار متمتیکا به عنوان یک برنامه کاربردی کامل در حوزه ریاضیات قابلیت‌های زیاد و گسترده‌ای دارد که در این مجال نمی‌توان به همه آن‌ها پرداخت. همانطور که دیدید دستورات برای رسم نمودار در متمتیکا بسیار متنوع و هر یک کاربرد خاص خود را دارند.