آزمون رگرسیون خطی در SPSS — راهنمای کاربردی

رگرسیون یا به اصطلاح «معادله خط برگشت» (Regression Line Equation) یک تکنیک آماری است که در بسیاری از حوزههای علمی، بخصوص «یادگیری ماشین» (Machine Learning) و «دادهکاوی» (Data Mining) کاربرد دارد. از آنجا که محاسبات برای اجرای رگرسیون خطی، زمانبر و طولانی است و باید دقیق باشد، در اغلب موارد از نرمافزارهای محاسبات آماری مانند SPSS برای انجام این کار استفاده میکنند. به همین دلیل نیز در این نوشتار به تکنیک و آزمون رگرسیون خطی در SPSS پرداخته و با ذکر مثالی، مراحل انجام این کار را مرور خواهیم کرد.
برای آشنایی بیشتر با فرمولهای محاسباتی رگرسیون خطی ساده و همچنین کاربردهای رگرسیون خطی، مطالب دیگر مجله فرادرس با عنوانهای رگرسیون خطی — مفهوم و محاسبات به زبان ساده و ضریبهای همبستگی (Correlation Coefficients) و شیوه محاسبه آنها — به زبان ساده را مطالعه کنید. همچنین خواندن نوشتارهای رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده و تحلیل واریانس (Anova) — مفاهیم و کاربردها نیز خالی از لطف نیست.
آزمون رگرسیون خطی ساده در SPSS
مدل سازی بخصوص مدل خطی که میتواند سادهترین مدل برازش برای دادهها در حوزه علوم آماری باشد، در بیشتر شاخههای علوم دیگر مانند «هوشمصنوعی» و «دادهکاوی» به کار میرود. یکی از سادهترین و از طرفی، موثرترین روشهای ساخت مدل خطی، «رگرسیون» (Regression) یا «معادله خط برگشت» نام دارد. همانطور که از نام این تکنیک بر میآید، به دنبال ساخت مدلی هستیم که به واسطه معادله یک خط نوشته میشود. قرار است به کمک زوج دادههای موجود، ضریب زاویه و همچنین عرض از مبدا چنین خطی را محاسبه کنیم.
این خط میتوان بیانگر رابطه خطی بین «متغیرهای پاسخ» (Response Variable) و «متغیرهای توصیفی» (Exploratory Variables) باشد. شایان ذکر است که گاهی به متغیرهای پاسخ، «متغیرهای وابسته» (Dependent Variable) و به متغیرهای توصیفی نیز «متغیرهای مستقل» (Independent Variable) یا متغیرهای پیشگو میگویند.
البته ممکن است رابطه بین متغیر (یا مشاهدات) وابسته و مستقل، به صورت خطی نباشد. در این هنگام شاید برازش یک منحنی به دادهها، بتواند واقعیت را بهتر نشان داده و مدل مناسبی برای نمایش ارتباط بین متغیرهای مستقل و وابسته باشد. منحنی یا تابعی که از بیشتر نقطهها یا دادهها، عبور یا کمترین فاصله را داشته باشد، بهترین منحنی را معرفی میکند. اگر منحنی مورد نظر از همه نقاط عبور نماید، بیشترین دقت و بهترین برازش را دارد. از طرفی اگر فاصله نقطهها از این منحنی نسبت به منحنیهای دیگر کمتر باشد، میتوان به یک برازش ایدهآل رسید.
در رگرسیون خطی، منحنی مورد بحث، در حقیقت یک خط راست است. بنابراین به جای معادله یا تابعی که منحنی را بیان میکند، از معادله خط (که سادهترین رابطه و معادله محسوب میشود) استفاده میشود. همانطور که به یاد دارید معادله خط به صورت استاندارد به فرم زیر قابل بیان است.
$$ \large y = a + bx $$
در رابطه بالا، $$a$$ را «عرض از مبدا» (Intercept) و $$b$$ را «شیب خط» (Slop) میگویند. بنابراین در مدل رگرسیونی، هدف برآورد این دو پارامتر است. از آنجایی که دادههای جمعآوری شده، به صورت زوج مرتب هستند، آنها را به شکل $$(x,y)$$ نشان میدهیم. در حالت کلی رابطهای که بین نقطههای نمونه حاصل از جامعه آماری در رگرسیون خطی ساده در نظر گرفته میشود به صورت زیر است.
$$ \large y = a + b x + e $$
جمله یا عبارت $$e$$، عبارت خطا نامیده شده و ماهیت تصادفی بودن دادهها را نشان میدهد. یکی از شرطهای مهم در معادله رگرسیونی، آن است که میانگین خطا باید برابر با صفر باشد. به این ترتیب نشان میدهیم که انتظار داریم خطاهای با مقدار مثبت و خطایهای با مقدار منفی برای نقطههای پیشبینی شده، در مجموع یکدیگر را خنثی کنند.
بنابراین یک رابطه رگرسیونی را به شکل زیر نشان میدهند. منظور از $$E$$، امید ریاضی یا همان مقدار مورد انتظار است.
$$ \large E(y) = \widehat{a} + \widehat{b}\; x $$
علامت $$\widehat{}$$ نشانگر برآورد برای هر یک از این پارامترها است. در اغلب موارد، نرمافزارهای محاسبات رایانهای، از حرف $$B$$ یا $$\widehat{\beta}$$ برای نمایش برآوردگر پارامتر ضریب و $$constant$$ برای عرض از مبدا استفاده میکنند. برای بدست آوردن این برآوردگرها، «تکنیک کمترین مربعات خطا» (Ordinary Least Square) یا OLS به کار میرود.
شرطهای اولیه برای اجرای رگرسیون با تکنیک OLS به صورت فهرستوار ارائه شدهاند. برای اطلاعات بیشتر در این زمینه میتوانید، رگرسیون خطی در پایتون — مفاهیم اساسی (بخش اول) را مطالعه کنید.
- بررسی نرمال بودن باقیماندهها
- تصادفی بودن باقیماندهها
- ثابت بودن واریانس
- استقلال متغیرهای توصیفی (مستقل)
البته از آنجایی که در مدل و آزمون رگرسیون خطی فقط از یک متغیر مستقل استفاده میکنیم، شرط استقلال موردی نخواهد داشت.
اجرای مدل و آزمون رگرسیون خطی در SPSS
این بخش از متن به نحوه اجرا و آزمون رگرسیون خطی در SPSS اختصاص دارد. البته به شرطهایی که برای اجرای رگرسیون خطی با روش OLS مورد نیاز است، خواهیم پرداخت. به این منظور از یک فایل اطلاعاتی استفاده میکنیم و مثال مربوط به آزمون رگرسیون خطی در SPSS را جلو میبریم. برای دسترسی به این فایل با قالب فشرده، اینجا کلیک کنید. پس از اینکه فایل را از حالت فشرده خارج کردید، میتوانید آن را در نرمافزار SPSS بارگذاری کرده و استفاده نمایید.
ابتدا به اطلاعاتی که در این فایل ثبت شده نگاهی میاندازیم. همانطور که در تصویر ۱ مشاهده میکنید، این مجموعه داده مربوط به ده کارمند است که اسامی آنها در ستون fname نوشته شده است. همچنین «ضریب هوش» (iq) که یک متغیر کمی است، به همراه «کارایی» (performance) نیز در این فایل اطلاعاتی ثبت شده است. به نظر میرسد که کارایی افراد باید با ضریب هوشی آنها در رابطه باشد. به این معنی که هر چه ضریب هوشی بیشتر باشد، کارایی نیز بیشتر خواهد بود. پس انتظار داریم رابطه بین این دو متغیر از نوع مستقیم باشد.
پس فرض میکنیم که میتوانیم براساس «ضریب هوش» (iq)، قادر به پیشگویی «کارایی» (performance) کارکنان باشیم. این امر میتواند ما را در استخدام کارمندان جدید یاری رساند. به این ترتیب قبل از استخدام، با اندازهگیری ضریب هوشی افراد این امکان را داریم که میزان کارایی آنها را در شرکت پیشبینی کنیم و بهترین فرد یا افراد را به استخدام درآوریم.
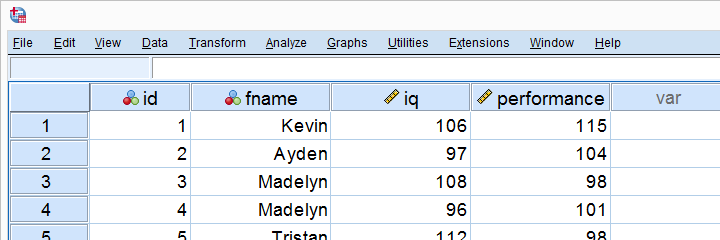

همانطور که در تصویر ۱ مشاهده میشود، متغیرهای مورد استفاده در مدل رگرسیونی، iq با برچسب IQ test score و Performance با برچسب Job performace test score هستند. این دو متغیر از نوع Scale بوده که مشخص میکند مقادیر مورد نظر برایشان از نوع کمّی است. متغیرهای id و fname در طراحی مدل نقشی نخواهند داشت. مدل ارائه شده توسط تکنیک رگرسیونی، دادههایی موجود از کارکنان شرکت را دریافت کرده و یک معادله خطی بین میزان هوش و کارایی به صورت زیر ارائه میکند.
$$ \large \text{performance} = \;a + b\; \text{iq} $$
بنابراین هدف پیدا کردن مقادیر $$a$$ و $$b$$ است.
بررسی رابطه خطی بین متغیرها
بهتر است قبل از ایجاد مدل رگرسیونی، وجود رابطه خطی بین متغیرها را بوسیله یک «نمودار نقطهای» (Scatter/Dot Plot) مشخص کنیم. کد زیر را در پنجره Syntax نرمافزار SPSS وارد کرده و اجرا نمایید. همانطور که مشاهده میکنید، تابع یا رویه graph برای رسم نمودار نقطهای به کار رفته است.
1*Scatterplot with title and subtitle from Graphs -> Legacy Dialogs -> Scatter.
2
3GRAPH
4/SCATTERPLOT(BIVAR)=iq WITH performance
5/MISSING=LISTWISE
6/TITLE='Scatterplot Performance with IQ'
7/subtitle 'All Respondents | N = 10'.البته این کار را با استفاده از فهرست دستورات (Menu) و گزینه Graph و طی کردن مسیر زیر نیز میتوانید انجام دهید.
Graph - Legacy Dialogs - Scatter/Dot
تنظیمات مربوط به ترسیم نمودار پراکندگی/نقطهای در تصویر ۲ دیده میشود.
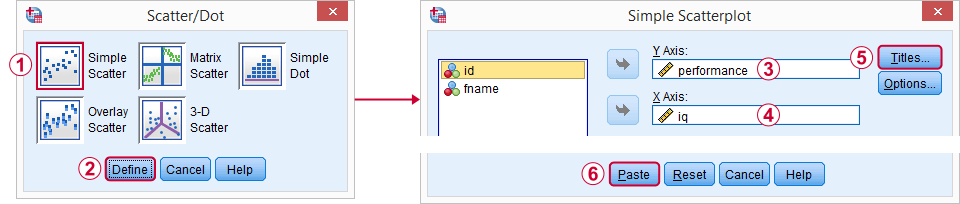
گامیهایی که برای اجری این کارها لازم است به ترتیب شمارهگذاری شدهاند. از آنجایی برای رسم توابع، متغیر مستقل را در محور افقی و متغیر (تابع) را در محور عمودی نشان میدهند، در پنجره Simple Scatterplot هم متغیر iq را در محور افقی (X Axis) و performance را در محور عمودی (Y Axis) قرار دادهایم.
با انتخاب دکمه Titles میتوانید برای نمودار عنوان انتخاب کنید. مطابق با کد بالا، عنوان را به صورت Scatterplot Performance with IQ و زیر عنوان نیز به صورت All Respondents | N = 10 در نظر گرفته میشود.
با فشردن دکمه Paste، کد مربوط به اجرای این دستور در پنجره Syntax ظاهر خواهد شد و باید کد مورد نظر را اجرا کنید. ولی با فشردن دکمه OK عملیات محاسبات صورت گرفته و خروجی را در پنجره Output مشاهده خواهید کرد. نتیجه اجرای دستورات به صورت نموداری که در تصویر ۳ مشاهده میشود، ظاهر خواهد شد.
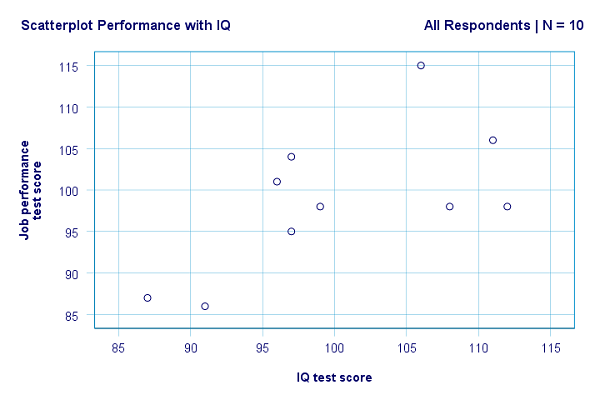
هر چند تعداد دادهها کم است (N = 10) ولی باز هم میتوان خطی فرضی برای نمایش ارتباط تقریبی بین این نقطهها را در نظر گرفت. در ادامه سعی میکنیم این خط را در نمودار ظاهر کنیم. به این منظور نمودار را به حالت ویرایش در میآوریم. روی نمودار دوبار کلیک کنید تا پنجره Chart Editor باز شود. در این حالت قادر به تغییر قالببندی و ساختار نمودار خواهید بود. همانطور که در تصویر ۴ مشاهده میکنید، انتخاب دکمه Add Fit Line at Total، میتواند یک خط رگرسیونی را برآورد کرده و روی نمودار ظاهر سازد.
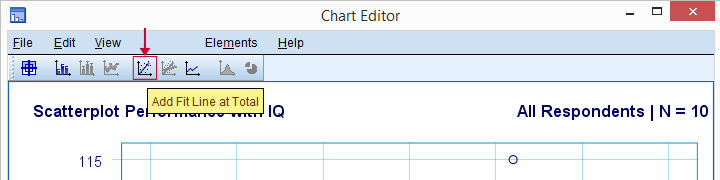
معادله خطی حاصل در تصویر ۵ قابل مشاهده است. از طرفی مربع ضریب همبستگی بین مقادیر واقعی و پیشبینی شده برای متغیر وابسته یا همان یا ضریب تعیین ($$R^2$$) نیز در نمودار دیده میشود. البته مقدار کوچک برای $$R^2$$ نشانگر ضعف در مدل رگرسیونی است. در اینجا هم $$R^2 = 0.403$$ مقدار کوچکی است و نمیتوان به طور کامل رابطه بین متغیر وابسته و مستقل را خطی در نظر گرفت. شاید یکی از علتهای اصلی در این حالت، کم بودن تعداد مشاهدات باشد. ولی به هر حال برای اجرای مدل رگرسیونی کار را ادامه خواهیم داد.

برآورد پارامترهای مدل و آزمون رگرسیون خطی در SPSS
برای اجرای و برآورد پارامترها و همچنین آزمون رگرسیون خطی در SPSS باید از مسیر زیر، دستور Linear Regression را اجرا کنیم.
Analyze - Regression - Linear
با انجام این کار پنجرهای به نام Linear Regression مانند تصویر ۶، ظاهر خواهد شد. مراحل تعیین پارامترهای این پنجره در تصویر زیر به خوبی نشان داده شده است. با انتخاب دکمه Statistics میتوانید بعضی از شاخصهای مناسب برای متغیرها، نظیر «برآورد پارامترها» (Estimated) و همچنین «فاصله اطمینان» (Confidence intervals) را درخواست کنید. همچنین انتخاب Model fit، برآوردها و انجام آزمون برای آنها را صورت خواهد داد.
همچنین برای نمایش ثابت بودن واریانس باقیماندهها، از دکمه Plots استفاده کرده و نموداری برحسب ZPRED و ZRESID رسم کردهایم. مشخص است که ZPRED نمایانگر مقادیر پیشبینی شده برای متغیر وابسته است که به صورت استاندار درآمده و ZRESID نیز باقیماندهها یا همان برآورد خطای استاندارد شده است.
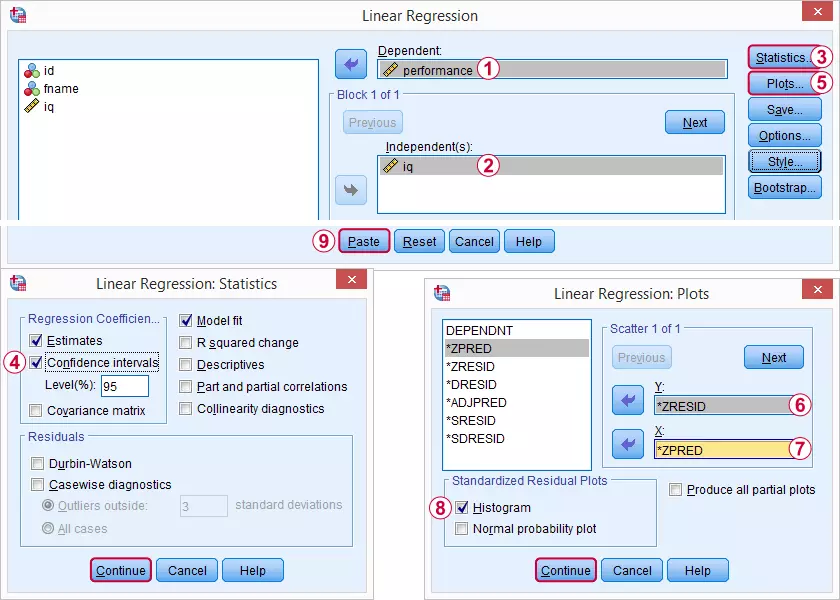
قطعه کدی که در ادامه مشاهده میکنید به منظور اجرای رگرسیون خطی و ترسیم نمودار باقیماندهها نوشته شده است. البته فشردن دکمه Paste در پنجره Linear Regression نیز همین کد را، با توجه به تنظیمات صورت گرفته، تولید خواهد کرد.
1*Simple regression with residual plots and confidence intervals.
2
3REGRESSION
4/MISSING LISTWISE
5/STATISTICS COEFF OUTS CI(95) R ANOVA
6/CRITERIA=PIN(.05) POUT(.10)
7/NOORIGIN
8/DEPENDENT performance
9/METHOD=ENTER iq
10/SCATTERPLOT=(*ZRESID ,*ZPRED)
11/RESIDUALS HISTOGRAM(ZRESID).نتیجه محاسبات مطابق با جدولهایی که در تصویرهای بعدی مشاهده میکنید، در پنجره خروجی SPSS قرار میگیرند. ابتدا متغیرهای وابسته و مستقل در جدول Variables Entered/Removed مشخص میشوند. مشخص است که متغیر iq به عنوان متغیر مستقل وارد مدل شده و برای پیشبینی متغیر performance به کار رفته است.
در جدولی که در تصویر 7 مشاهده میکنید، ضریب همبستگی بین مقادیر پیش بینی شده و مقدارهای واقعی متغیر مستقل محاسبه شده. همچنین مربع ضریب همبستگی پیرسون که به «ضریب تعیین» (Coefficient of Determination) معروف است، در ستون R Square قرار گرفته. ضریب تعیین نشانگر درصدی از تغییرات متغیر وابسته است که توسط مدل رگرسیونی قابل تخمین است. هر چه ضریب تعیین بزرگتر و به یک نزدیکتر باشد، مدل رگرسیونی مناسبتر است.

در بخش بعدی جدول آنالیز واریانس (ANOVA) و برآورد پارامترها را مشاهده میکنید. با توجه به مقدار Sig در جدول Anova میتوان گفت که مدل رگرسیونی توانسته است، نسبت به حالت تصادفی، واریانس متغیر وابسته را بیشتر توصیف کند، زیرا sig = 0٫049 کمتر از احتمال خطای اول 0٫05 = $$\alpha$$ است.
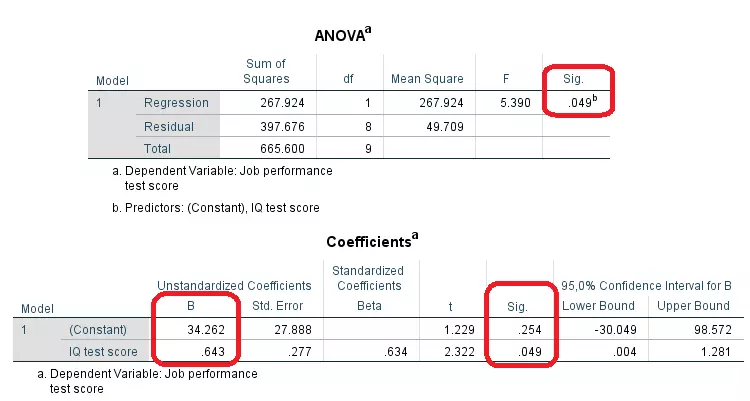
ضرایب رگرسیونی یا همان برآورد پارامترها هم در جدول Coefficients ظاهر شده. مقدار ثابت یا همان «عرض از مبدا» برابر با ۳۴٫۲۶۲ و «شیب خط» نیز ۰٫۶۴۳ بدست آمده. بنابراین معادله خط به صورت زیر در خواهد آمد. توجه داشته باشید که حرف a در بالای نام این جدول در پایین به صورت زیرنویس توضیح داده شده. این شرح، مشخص میکند که متغیر وابسته در مدل رگرسیونی، Job performance test score است.
$$ \large \text{performance} = 34.262 + 0.643 \text{ iq} $$
همانطور که میبینید، این معادله با معادلهای خطی که در نمودار مربوط به تصویر ۵ دیده میشود، مطابقت دارد. ولی به این موضوع نیز توجه داشته باشید که مقدار Sig برای ردیف Constant بزرگتر از ۰٫۰۵ است و این امر میتواند، فرض صفر بودن مقدار ثابت را تقویت کند. ولی از طرفی مقدار Sig برای متغیر IQ test score کمتر از ۰٫۰۵ بوده که نشانگر معنیدار بودن این پارامتر یا متغیر است. بنابراین میزان هوش با کارایی در ارتباط بوده ولی ممکن است رابطه به شکل خطی نباشد.
در جدول مربوط به بررسی «باقیماندهها» (Residuals) نیز شاخصهای توصیفی برای باقیماندههای استاندارد شده و مقدارهای پیشبینی شده نمایش داده شده. همانطور که دیده میشود، «میانگین» (Mean) برآورد خطا یا باقی ماندهها صفر است که در شرایط گفته شده صدق میکند.
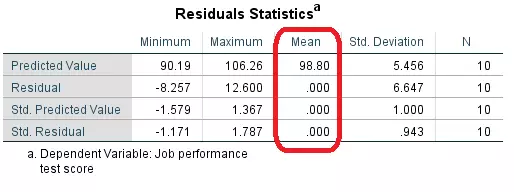
نمودار رسم شده برای مقایسه باقیماندههای استاندارد نسبت به مقادیر پیشبینی شده استاندارد نیز در تصویر ۱۰ دیده میشود. فرض تصادفی و ثابت بودن واریانس برای آزمون رگرسیون خطی در SPSS در این نمودار دیده میشود. اگر تغییرات باقیمانده در این نمودار به صورت افزایشی بود، میتوانستیم واریانس را صعودی و غیر ثابت در نظر بگیریم و شرط رگرسیون OLS را مخدوش اعلام کنیم. ولی خوشبختانه این نمودار چنین چیزی را نشان نمیدهد.
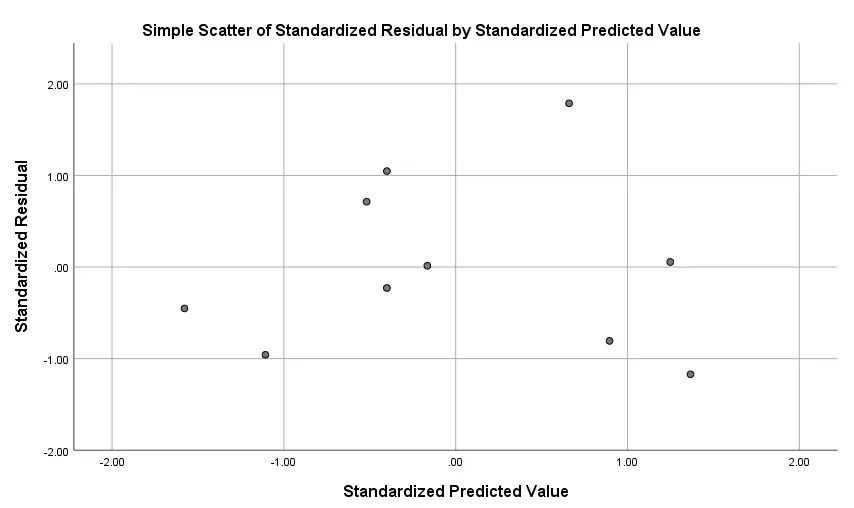
همانطور که در تصویر ۱۰ مشاهده میکنید، حدود تغییرات روی هر دو محور به علت استاندارد کردن مقادیر، در بازه ۲- تا ۲ است.
با توجه به درخواست مربوط به ترسیم «نمودار هیستوگرام» (Histogram) در تنظیمات پنجره plot، نموداری که در تصویر ۱۱ مشاهده میکنید، ترسیم خواهد شد و به کمک آن میتوانیم نرمال بودن متغیر وابسته (یا خطا) را برای مدل و آزمون رگرسیون خطی در SPSS مورد بررسی قرار داد.

البته با توجه به تصویر ۱1، مشخص است که توزیع باقیماندهها با توزیع نرمال، فاصله زیادی دارد. پس یکی از شرطهای مهم در رگرسیون OLS نقض شده است. با توجه به اینکه ضریب تعیین هم مقدار کوچکی بدست آمد، بهتر است این مدل را با دادههای بیشتری برازش کرده تا نتایج قابلیت اطمینان بیشتری داشته باشند.
در صورتی که باز هم شرایط مربوط به مدل OLS نقض شود، مدل مناسب توسط روشهای ناپارامتری یا تکنیکهای دیگر رگرسیون بدست خواهد آمد. پیشنهاد میشود متن انواع روش های رگرسیونی — راهنمای جامع را در این رابطه مطالعه کنید.
خلاصه و جمعبندی
در این نوشتار به شیوه اجرا و آزمون رگرسیون خطی در SPSS آشنا شده و به کمک مثالی، روند اجرای محاسبات را برایتان بازگو کردیم. همانطور که دیدید، مدل رگرسیونی باید دارای شرایطی باشد تا نتیجه حاصل قابل اتکا باشد. اگر این پیشفرضها محقق نشوند، نمیتوان مقدارهای پیش بینی شده توسط مدل یا خط رگرسیونی را معتبر دانست. در چنین مواقعی بهتر است از شیوههای دیگر تکنیک رگرسیون مانند روشهای رگرسیون ناپارامتری یا رگرسیون غیر خطی استفاده کرد. رسم منحنیها و نمودارها، به درک مدل خطی در آزمون رگرسیون خطی در SPSS کمک شایانی میکند. به همین دلیل در این نوشتار هم به بررسی نحوه ترسیم این نمودارها پرداختیم.











سلام آقای ری بد
متشکرم از توضیحات شما
بنده یک سوال داشتم مقدار sig مربوط به عرض از مبدا بیشتر از 0.05 است و یعنی دلیلی برای رد فرضیه صفر نداریم.
به عبارتی مدل بدون عرض از مبدا است.
آیا من اشتباه میکنم؟
ممنون میشوم راهنمایی بفرمایید.
درود بر شما و خداقوت
از مجموعه آموزشهایی که در زمینه رگرسیون داشتید برای انجام یک پروژه آماری استفاده کردم و نتیجه عالی بود.
سپاس از مجموعه خوب فرادرس بابت فراهم کردن چنین آموزشهای مفیدی
و همچنین سپاس از شما استاد فرهیخته گرامی بابت ارائه مطالب بصورت مفید و جامع و بسیار کاربردی
تندرست باشید و پیروز
خیلی خوب و آموزنده بود.
سلام جناب استاد ری بد اگر بخواهیم مدل رگرسیون خطی ارزیابی کنیم که در مقابل متغیر های جدید چگونه عملکرد دارد باید چکار کنیم ؟
خیلی ممنون ساده و روان و بسیار مفید بود
سلام
برای فصل چهار چه اطلاعاتی از جداول رگرسیون باید در جداول اورد
ممنون میشم راهنمایی بفرمایید .