انواع روش های رگرسیونی — راهنمای جامع

در دیگر نوشتارهای مجله فرادرس با مفهوم رگرسیون خطی و همچنین نحوه محاسبات آن آشنا شده‌‌اید. در این نوشتار با انواع روش های رگرسیونی خطی (Linear) و غیرخطی (NonLinear) آشنا خواهیم شد و کدهایی مربوط به پیاده‌سازی آن‌ها را در زبان برنامه‌نویسی R، فرا می‌گیریم. در این بین ابتدا با مفاهیم اولیه رگرسیون و سپس دستورات و کدهای R که تکنیک‌های مختلف رگرسیونی را اجرا می‌کنند، آشنا می‌شویم. از آنجایی که تکنیک‌های رگرسیونی برای داده‌های کیفی و کمی، به شکلی جداگانه‌ و متفاوت اجرا می‌شوند، اطلاع از نحوه اجرا این تکنیک‌های رگرسیونی در این حالت‌ها بسیار ضروری است، بخصوص برای کسانی که می‌خواهند در حوزه «علم داده» (Data Science) فعالیت کنند.

برای آشنایی بیشتر با مفاهیم اولیه در رگرسیون خطی، نوشتارهای رگرسیون خطی — مفهوم و محاسبات به زبان ساده، رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده را بخوانید. همچنین خواندن مطلب هم خطی در مدل رگرسیونی — به زبان ساده و آموزش رگرسیون — مجموعه مقالات جامع وبلاگ فرادرس نیز خالی از لطف نیست.

انواع روش های رگرسیونی

اغلب کسانی که با مدل‌های رگرسیونی سر و کار دارند، از دو یا سه شیوه عمومی استفاده می‌کنند. در حالیکه تکنیک‌های رگرسیونی بسیار گسترده‌تر هستند و به منظور تحلیل‌های مختلف روی داده‌های کیفی و کمی به شکل‌های متفاوتی به کار می‌روند. در این نوشتار به 14 روش رگرسیونی اشاره می‌کنیم و کدهای مربوط به پیاده‌سازی آن‌ها را در زبان برنامه‌نویسی و محاسبات آماری R، فرا می‌گیریم. این تکنیک‌ها رگرسیونی در زیر به صورت فهرست‌وار معرفی شده‌اند.

1. رگرسیون خطی (Linear Regression)
2. رگرسیون لجستیک (Logistic Regression)
3. رگرسیون چندکی (Quantile Regression)
4. رگرسیون ستیغی (Ridge Regression)
5. رگرسیون لاسو (Lasso Regression)
6. رگرسیون شبکه الاستیک (Elastic Net Regression)
7. رگرسیون مولفه‌های اصلی (Principle Component Regression)
8. رگرسیون کمترین مربعات جزئی (Partial Least Square (PLS) Regression)
9. رگرسیون بردار پشتیبان (Support Vector Regression)
10. رگرسیون ترتیبی (Ordinal Regression)
11. رگرسیون پواسون (Poisson Regression)
12. رگرسیون دوجمله‌ای منفی (Negative Binomial Regression)
13. رگرسیون شبه پواسن (Quasi Poisson Regression)
14. رگرسیون کاکس (Cox Regression)

آگاهی از این روش‌ها به یک «دانشمند داده» (Data Scientist) کمک می‌کند که بهترین روش و الگو را برای تحلیل داده‌های خود به کار ببرد و در نتیجه مدل‌های ساخته شده از بیشترین کارایی و دقت برخوردار شوند.

هر یک از روش‌های رگرسیونی، پیش‌فرض‌های مخصوص خود را دارد که برحسب ویژگی و مشخصات «متغیرهای توصیفی» (Explanatory Variables) و «متغیر پاسخ» (Response Variable) تعیین می‌شوند. توجه داشته باشید که گاهی به متغیرهای توصیفی، «متغیرهای مستقل» (Independent Variable) و به متغیر پاسخ، «متغیر وابسته» (Dependent Variable) می‌گویند. البته اصطلاح متغیرهای «رگرسور» (Regressor) یا «پیشگو» (Predictor) نیز گاهی برای متغیرهای توصیفی به کار می‌رود.

فرضیه‌های صحت مدل رگرسیونی

قبل از اجرای مدل رگرسیونی باید بوسیله رسم نمودار یا محاسبه ضریب همبستگی و نظایر آن، وجود وابستگی بین متغیرها توصیفی با متغیر وابسته را مورد بررسی قرار دهیم و در صورتی که نتایج حاصل از این ابزارها، نشانگر وجود رابطه (رابطه خطی یا رابطه غیر خطی) بین این دو دسته متغیر باشد، به دنبال ایجاد مدل رگرسیونی باشیم.

ولی در اینجا هم کار تمام نشده است. پس از محاسبات و برآورد پارامترهای مدل باید فرضیه‌هایی که مدل رگرسیونی براساس آن استوار شده است نیز آزمون شود. بیشتر این گونه آزمون‌ها براساس باقی‌مانده‌های مدل صورت می‌گیرد در نتیجه باید آن‌ها را پس از پیدا کردن مدل و محاسبه باقی‌مانده‌ها (Residuals) مورد سنجش قرار داد.

این آزمون‌ها در فهرست زیر معرفی و توضیح داده شده‌اند. در ادامه با کدهایی از زبان R آشنا می‌شویم که این گونه آزمون‌ها را برایمان در مدل رگرسیونی اجرا می‌کنند.

• بررسی نقاط پرت (Outlier): از آنجایی که وجود نقاط دور افتاده یا پرت (Outlier)، باعث می‌شود که برآورد پارامترهای مدل رگرسیونی به درستی صورت نگیرد، قبل از اجرای محاسبات مربوط به مدل رگرسیونی باید از عدم چنین داده‌های اطمینان حاصل پیدا کنیم و اگر به این گونه مشاهدات برخوردیم، آن‌ها را از مدل خارج کرده، سپس دوباره مدل‌سازی را انجام دهیم. نقاط پرت در اینجا به مشاهداتی اشاره دارد که باقی‌مانده‌های خیلی بزرگی نسبت به بقیه نقاط دارند.
• هم‌خطی و هم‌خطی چندگانه: اگر متغیرهای توصیفی نسبت به هم وابستگی داشته باشند، پارامترهای مدل، واریانس بزرگی پیدا کرده، در نتیجه قابل اعتماد نیستند. در این حالت باید مدل رگرسیونی را از جهت وجود مشکل هم‌خطی (Colinearity)  یا  هم‌خطی چندگانه (Multicolinearity) مورد بررسی قرار داد.
• ناهم‌واریانسی (Heteroscedasticity): باقی‌مانده‌های حاصل از مدل رگرسیونی باید دارای واریانس ثابت باشند. معمولا این موضوع به متغیر وابسته نیز بر می‌گردد. اگر با تغییر مقادیر متغیرهای توصیفی، واریانس متغیر وابسته تغییر کند، با مشکل ناهم‌واریانس مواجه هستیم. وزن‌دهی به مشاهدات یا تبدیل روی متغیر وابسته، روش‌هایی برای ثابت کردن واریانس متغیر پاسخ محسوب می‌شوند.
• بیش‌برازش و کم‌برازش (Under and Over Fitting): به کارگیری متغیرهای توصیفی زیاد در کاهش میزان خطای مدل رگرسیونی موثر است ولی در این صورت ممکن است مدل دچار مشکل «بیش‌برازش» (Overfitting) شود. به این معنی که مدل قادر به پیش‌بینی دقیق مقادیر متغیر پاسخ برای مشاهداتی است براساس آن مدل ساخته شده ولی برای داده‌های جدید، توانایی پیش‌بینی مناسب را ندارد. عکس این حالت که کم‌برازش (Underfitting) نامیده می‌شود، ناکافی بودن متغیرهای توصیفی در مدل است، بطوری که واریانس مقادیر پیش‌بینی بسیار زیاد خواهد بود. به این ترتیب باید از مدل رگرسیونی استفاده کرد که تعداد متغیرهای آن مناسب بوده و چنین مسائلی را بوجود نیاورد.

۱. رگرسیون خطی

یکی از ساده‌ترین تکنیک‌های رگرسیون، رگرسیون خطی (Linear Regression) است که در آن متغیر پاسخ یا متغیر وابسته مقادیر عددی و پیوسته دارند. در این حالت رابطه بین متغیر وابسته و مستقل، یک رابطه خطی برحسب پارامترهای مدل است. چنین حالتی را در تصویر زیر مشاهده می‌کنید.

زمانی که فقط یک متغیر مستقل وجود داشته باشد، مدل رگرسیونی خطی را ساده (Simple Regression) می‌نامند و اگر بیش از یک متغیر مستقل (توصیفی) وجود داشته باشد، رگرسیون را چندگانه (Multiple Regression) می‌گویند.

در اینجا، پارامترهای مدل، بوسیله کمینه‌سازی «مجموع مربعات خطا» (Sum of Square Error) صورت می‌گیرد که به این تکنیک، «رگرسیون عادی» (Ordinary Least Square) یا OLS نیز گفته می‌شود.

برای برازش و اجرای رگرسیون خطی، از مجموعه داده swiss که در بسته datasets از زبان R قرار دارد، استفاده می‌کنیم. ابتدا به این مجموعه داده نگاهی می‌اندازیم. برای دسترسی به این مجموعه کافی است کتابخانه datasets را بارگذاری کنید. البته از اینجا نیز این مجموعه داده با قالب فشرده را می‌توانید دریافت کنید. توجه داشته باشید که پس از خارج کردن این فایل از حالت فشرده، به یک فایل csv برخورد خواهید کرد که با دستور read.csv در R قابل بارگذاری است.

مجموعه داده swiss شامل 47 مشاهده و شش متغیر است که مربوط به ویژگی‌های اقتصادی و رشد جمعیت در 47 ناحیه مختلف فرانسوی زبان کشور سوئیس هستند. متغیرهای مربوط به باروری (Fertility)، درصد جمعیت کشاورزان از کل (Agriculture)، درصد نفرات برتر در آزمون نظامی (Examination)،  درصد افراد با تحصیلات عالی (Education)، درصد کاتولیک‌ها (Catholic) و درصد فوت نوزادان کمتر از یک سال (Infant.Mortality) در سال 1888 در این فایل، ثبت شده‌اند.

library(datasets)
head(swiss)
             Fertility Agriculture Examination Education Catholic Infant.Mortality
Courtelary        80.2        17.0          15        12     9.96             22.2
Delemont          83.1        45.1           6         9    84.84             22.2
Franches-Mnt      92.5        39.7           5         5    93.40             20.2
Moutier           85.8        36.5          12         7    33.77             20.3
Neuveville        76.9        43.5          17        15     5.16             20.6
Porrentruy        76.1        35.3           9         7    90.57             26.6

به منظور انجام محاسبات و برآورد پارامترهای رگرسیون OLS از تابع lm در زبان‌ برنامه‌نویسی R استفاده می‌شود. در ادامه نمونه‌ای از کدهای مربوطه را مشاهده می‌کنید.

model = lm(Fertility ~ .,data = swiss)
lm_coeff = model$coefficients
lm_coeff
summary(model)

همانطور که مشخص است رابطه بین متغیر وابسته (Fertility) با بقیه متغیرها که نقش متغیرهای مستقل را ایفا می‌کنند به صورت زیر نوشته شده است. واضح است که مجموعه داده نیز swiss نام دارد. توجه داشته باشید که در اینجا بقیه متغیرها را با نماد «.» مشخص کرده‌ایم.

$$ \large lm (Fertility \sim . , data = swiss) $$

حاصل اجرای این کد به صورت زیر است:

   (Intercept)      Agriculture      Examination        Education         Catholic 
      66.9151817       -0.1721140       -0.2580082       -0.8709401        0.1041153 
Infant.Mortality 
       1.0770481 

lm(formula = Fertility ~ ., data = swiss)

Residuals:
     Min       1Q   Median       3Q      Max 
-15.2743  -5.2617   0.5032   4.1198  15.3213 

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)    
(Intercept)      66.91518   10.70604   6.250 1.91e-07 ***
Agriculture      -0.17211    0.07030  -2.448  0.01873 *  
Examination      -0.25801    0.25388  -1.016  0.31546    
Education        -0.87094    0.18303  -4.758 2.43e-05 ***
Catholic          0.10412    0.03526   2.953  0.00519 ** 
Infant.Mortality  1.07705    0.38172   2.822  0.00734 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 7.165 on 41 degrees of freedom
Multiple R-squared:  0.7067, Adjusted R-squared:  0.671 
F-statistic: 19.76 on 5 and 41 DF,  p-value: 5.594e-10

براساس خروجی‌ها و مقدار R-squared که برابر با 0٫7067 است،‌ می‌توان گفت که حدود ۷۰ درصد تغییرات متغیر وابسته، برحسب مدل بیان شده. همچنین در ستون (|Pr(>|t که همان «مقدار احتمال» (p-Value) است می‌توان همه پارامترها به جز پارامتر Examination را معنی‌دار (Significant) دانست. معنی‌دار بودن از لحاظ آماری در اینجا به معنی مخالف صفر بودن پارامتر است. به این ترتیب می‌توان حضور آن را در مدل، معنی‌دار در نظر گرفت.

نکته: متغیر یا پارامترهایی که از لحاظ آماری، معنی‌دار (مخالف صفر) هستند با علامت * در خروجی تابع lm مشخص شده‌اند.

۲. رگرسیون لجستیک

در رگرسیون لجستیک (Logistic Regression)، متغیر وابسته، به صورت دو دویی (Binary) است. به این معنی که مقادیر آن به دو طبقه صفر و یک دسته‌بندی شده‌اند. البته زمانی که از رگرسیون چند جمله‌ای لجستیک (Multinomial Logistic Regression) استفاده می‌کنید، ممکن است تعداد سطوح متغیر طبقه‌ای بیشتر از دو باشد. در این حال مدل رگرسیون لجستیک به شکل زیر نوشته می‌شود.

$$ \large P(Y = 1) = \dfrac{1}{1 + e^{ -(\beta_0 + \beta_1X_1 + \beta_2X_2 + \ldots + \beta_kX_k)}} $$

واضح است که در این مدل رگرسیونی، خطاها، دارای توزیع نرمال نیستند و متغیر وابسته دارای توزیع دو یا چند جمله‌ای است در نتیجه نمی‌توان از مدل رگرسیون ساده یا خطی استفاده کرد.

نکته: معمولا از این شیوه یا مدل رگرسیونی، برای طبقه‌بندی کردن مشاهدات جدید برحسب مقادیر قبلی استفاده می‌کنند و به نوع «یادگیری نظارت شده» (Supervised Learning) محسوب می‌شود. به این ترتیب اگر مقدار $$P(Y=1)$$ از یک مقدار آستانه (مثلا 0٫5) بیشتر باشد، آن مشاهده را در گروه ۱ طبقه‌بندی می‌کنیم.

برای اجرای رگرسیون لجستیک، از مجموعه داده‌های سرطان سینه (case2002) که در بسته یا کتابخانه Sleuth2 قرار دارد، استفاده می‌کنیم. این مجموعه داده شامل 147 مشاهده و 7 متغیر است. نمونه‌ای از اطلاعات مربوط به این داده‌ها را در ادامه مشاهده می‌کنید. اگر دسترسی به این کتابخانه برایتان مقدور نیست از اینجا نیز می‌توانید این فایل را دریافت و از حالت فشرده خارج کنید. یک فایل به نام case2002 از نوع csv در اختیارتان قرار خواهد گرفت که با دستور read.csv در R قابل بارگذاری است.

> head(case2002)
          LC   FM   SS     BK AG YR CD
1 LungCancer Male  Low   Bird 37 19 12
2 LungCancer Male  Low   Bird 41 22 15
3 LungCancer Male High NoBird 43 19 15
4 LungCancer Male  Low   Bird 46 24 15
5 LungCancer Male  Low   Bird 49 31 20
6 LungCancer Male High NoBird 51 24 15

قرار است براساس متغیر مصرف سیگار روزانه (CD)، تشخیص دهیم که فرد با چه احتمالی دچار سرطان سینه (LC) خواهد شد.

model <- glm(LC~CD,data = case2002, family = "binomial")
summary(model)

نتیجه اجرای این کد، محاسبه احتمال داشتن سرطان براساس تعداد سیگارهای کشیده شده در روز است.

glm(formula = LC ~ CD, family = "binomial", data = case2002)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-1.5148  -0.9688  -0.7166   1.3449   1.8603  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept) -1.53541    0.37707  -4.072 4.66e-05 ***
CD           0.05113    0.01939   2.637  0.00836 ** 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 187.14  on 146  degrees of freedom
Residual deviance: 179.62  on 145  degrees of freedom
AIC: 183.62

Number of Fisher Scoring iterations: 4

حال اگر مقادیر پیش‌بینی شده را ظاهر کنیم، احتمال ابتلا به سرطان برای افراد سیگاری مشاهده خواهد شد.

        1         2         3         4         5         6         7         8         9        10 
0.2845787 0.3168095 0.3168095 0.3168095 0.3745313 0.3168095 0.3745313 0.3745313 0.2642256 0.4360573 
       11        12        13        14        15        16        17        18        19        20 
0.6247508 0.4360573 0.3745313 0.4360573 0.3745313 0.4360573 0.4996171 0.3745313 0.3168095 0.3168095 
       21        22        23        24        25        26        27        28        29        30 
0.3168095 0.3745313 0.3745313 0.3168095 0.6247508 0.3745313 0.2642256 0.4996171 0.3745313 0.3168095 
       31        32        33        34        35        36        37        38        39        40 
0.3279782 0.2006837 0.3745313 0.2642256 0.4996171 0.4360573 0.2642256 0.3168095 0.3168095 0.4360573 
       41        42        43        44        45        46        47        48        49        50 
0.3745313 0.3745313 0.3745313 0.2264199 0.3745313 0.3168095 0.1772028 0.3745313 0.4360573 0.1926074 
       51        52        53        54        55        56        57        58        59        60 
0.3745313 0.4360573 0.2448299 0.3168095 0.4360573 0.3745313 0.6247508 0.2642256 0.2642256 0.2090110

از آنجایی که تعداد مشاهدات زیاد است، فقط برای ۶۰ نفر اول، نتایج را نشان داده‌ایم. حال داشتن سرطان را برای افراد سیگاری برحسب مقدار احتمال ۵۰٪ انجام می‌دهیم.

data$prediction <- model$fitted.values>0.5
data$prediction

به این ترتیب خروجی به صورت زیر در آمده و نشان می‌دهد که چه کسانی به احتمال زیاد مبتلا به سرطان خواهند شد. این امر با مقدار TRUE برای هر فرد مشخص شده است.

    1     2     3     4     5     6     7     8     9    10    11    12    13    14    15    16 
FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE 
   17    18    19    20    21    22    23    24    25    26    27    28    29    30    31    32 
FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE FALSE FALSE 
   33    34    35    36    37    38    39    40    41    42    43    44    45    46    47    48 
FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE 
   49    50    51    52    53    54    55    56    57    58    59    60    61    62    63    64 
FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE

۳. رگرسیون چندکی

رگرسیون چندکی (Quantile Regression) را می‌توان جایگزینی برای مدل رگرسیون خطی در نظر گرفت که نسبت به مشکلات حاصل از «نقاط دورافتاده یا پرت» (Outlier)، «چولگی زیاد» (High Skewness) و همچنین «ناهم‌واریانسی» (Heteroscedasticity) مقاوم است.

در رگرسیون خطی، میانگین متغیر وابسته به شرط مشاهدات برآورد می‌شود. در حقیقیت مدل رگرسیون خطی با در نظر گرفتن ماتریس $$X$$ و بردارهای $$\beta$$ و $$\alpha$$ به صورت زیر نوشته می‌شود.

$$ \large E(Y|x) = \alpha + \beta X $$

از آنجایی که میانگین جمله خطا را صفر در نظر گرفته‌ایم، در این عبارت مقدار خطا دیده نمی‌شود.

همانطور که می‌دانید میانگین با وجود داده‌های پرت، چولگی و ناهمواریانسی در متغیر وابسته، شاخص مناسبی به عنوان معیار تمرکز نیست. بنابراین شیوه رگرسیون خطی، نمی‌تواند تغییرات چنین متغیری را به خوبی توصیف و مدل مناسبی برای نمایش رابطه بین متغیر مستقل و وابسته ایجاد کند.

استفاده از چندک‌ها (Quantile) که نسبت به شرایط گفته شده، مقاوم‌تر هستند، می‌تواند مدل رگرسیون کامل‌تر و دقیق‌تری را ارائه کند. در رگرسیون چندکی به جای برآورد میانگین متغیر وابسته، از برآورد چندک‌های آن (مانند صدک، دهک یا چارک) به شرط متغیر مستقل، کمک گرفته می‌شود.

نکته: در رگرسیون چندکی، باید متغیر وابسته از نوع عددی و از نوع مقیاس (Scale) با مقادیر پیوسته باشد تا امکان محاسبه چندک‌ها وجود داشته باشد.

اگر $$Q_{Y|X}(p)$$ را چندک $$p$$ام متغیر وابسته $$Y$$ به شرط $$X$$ در نظر بگیریم، آنگاه مدل رگرسیون به صورت زیر خواهد بود.

$$ \large Q_{Y|X}(p) = X \beta_{p} $$

مشخص است که این مدل، بسیار شبیه رگرسیون خطی است. به همین علت گاهی رگرسیون چندکی را حالت توسعه یافته رگرسیون خطی می‌دانند. اگر برای مقادیر مختلف $$p$$ مدل رگرسیونی را پیش‌بینی کنیم و خطوط مربوطه را رسم کنیم، یک رگرسیون چندکی ایجاد کرده‌ایم.

نکته: توجه داشته باشید که کمینه‌سازی خطا طبق رابطه زیر صورت خواهد گرفت.

$$ \large p ( \sum |e_i|) + (1-p) \sum |e_i| $$

به این ترتیب اگر مقدار $$p=0.5$$ باشد، چندک به میانه تبدیل شده و مدل رگرسیونی را «رگرسیون میانه» (Median Regression) می‌نامند.

فرض کنید معادله رگرسیونی برای صدک ۲۵ام به صورت زیر بدست آمده باشد:

$$ \large Q_{y|x}(0.25) = 5 + 7x $$

در این صورت هر واحد اضافه شدن مقدار متغیر مستقل (x) باعث افزایش ۷ واحدی مقدار چندک ۲۵ام خواهد شد.

برای استفاده از رگرسیون چندکی در زبان برنامه‌نویسی R از بسته یا کتابخانه quantreg استفاده خواهیم کرد. در کد زیر نحوه نصب و بارگذاری این کتابخانه مشخص شده است.

install.packages("quantreg")
library(quantreg)

به کمک تابع rq امکان اجرای رگرسیون چندکی فراهم می‌شود. کدی که در زیر مشاهده می‌کنید به اجرای رگرسیون چندکی روی مجموعه داده swiss پرداخته است. در اینجا Fertility متغیر وابسته و بقیه متغیرها، مستقل محسوب شده‌اند.

model1 = rq(Fertility~.,data = swiss,tau = 0.25)
summary(model1)

مقدار $$p$$‌ در تابع rq به کمک پارامتر tau مشخص می‌شود. واضح است که در مدل اجرا شده، از صدک ۲۵ام (چارک اول) استفاد شده است. خروجی به صورت زیر خواهد بود.

tau: [1] 0.25
Coefficients:
                 coefficients lower bd upper bd
(Intercept)      76.63132      2.12518 93.99111
Agriculture      -0.18242     -0.44407  0.10603
Examination      -0.53411     -0.91580  0.63449
Education        -0.82689     -1.25865 -0.50734
Catholic          0.06116      0.00420  0.22848
Infant.Mortality  0.69341     -0.10562  2.36095

اگر مقدار tau را برابر با ۰٫۵ در نظر بگیریم، رگرسیون میانه را تولید خواهیم کرد.

model2 = rq(Fertility~.,data = swiss,tau = 0.5)
summary(model2)

خروجی به صورت زیر محاسبه خواهد شد.

tau: [1] 0.5
Coefficients:
                 coefficients lower bd upper bd
(Intercept)      63.49087     38.04597 87.66320
Agriculture      -0.20222     -0.32091 -0.05780
Examination      -0.45678     -1.04305  0.34613
Education        -0.79138     -1.25182 -0.06436
Catholic          0.10385      0.01947  0.15534
Infant.Mortality  1.45550      0.87146  2.21101

در این قسمت، رگرسیون چندکی را براساس صدک‌های پنجم تا ۹۵ام با فاصله ۵ درصدی اجرا خواهیم کرد.

model3 = rq(Fertility~.,data = swiss, tau = seq(0.05,0.95,by = 0.05))
quantplot = summary(model3)
quantplot
plot(quantplot)

خروجی به صورت زیر خواهد بود. البته به علت اینکه ۱۹ صدک‌ مختلف در این کد استفاده شده است، از نمایش همه خروجی‌ها صرف نظر کرده‌ایم و فقط صدک پنجم، پنجاهم و صدک ۹۵ را نمایش خواهیم دارد.

Call: rq(formula = Fertility ~ ., tau = seq(0.05, 0.95, by = 0.05), 
    data = swiss)
tau: [1] 0.05
Coefficients:
                 coefficients lower bd  upper bd 
(Intercept)       51.09373    -86.11344 137.77856
Agriculture       -0.07513     -0.61030   0.58050
Examination        0.25953     -1.09496   1.41414
Education         -1.22152     -2.59070  -0.63000
Catholic           0.14562     -0.54350   0.21595
Infant.Mortality   0.77762     -0.93163   4.32563
...
Call: rq(formula = Fertility ~ ., tau = seq(0.05, 0.95, by = 0.05), 
    data = swiss)
tau: [1] 0.5
Coefficients:
                 coefficients lower bd upper bd
(Intercept)      63.49087     38.04597 87.66320
Agriculture      -0.20222     -0.32091 -0.05780
Examination      -0.45678     -1.04305  0.34613
Education        -0.79138     -1.25182 -0.06436
Catholic          0.10385      0.01947  0.15534
Infant.Mortality  1.45550      0.87146  2.21101
...
Call: rq(formula = Fertility ~ ., tau = seq(0.05, 0.95, by = 0.05), 
    data = swiss)
tau: [1] 0.95
Coefficients:
                 coefficients lower bd  upper bd 
(Intercept)       75.46363     72.06874 101.45314
Agriculture       -0.08391     -0.86499   0.04293
Examination       -0.81276     -1.91404   1.38522
Education         -0.21915     -2.89058   2.24446
Catholic           0.09827     -0.10995   0.23662
Infant.Mortality   1.05260     -0.75085   1.18204

نمودارهای حاصل به شکل زیر ترسیم می‌شوند.

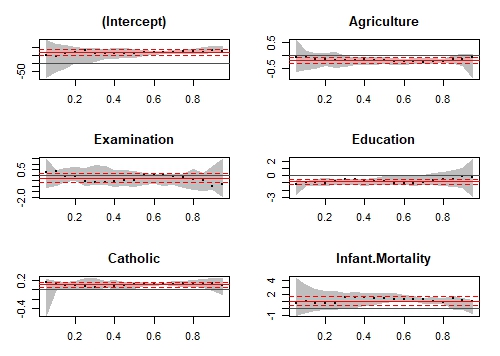
در این نمودارها، رگرسیون چندکی به ازاء هر یک از متغیرها مستقل ترسیم شده است. محور افقی، مقادیر چندک‌ها (از صدک پنجم تا صدک ۹۵ام) را نشان می‌دهد. محور عمودی نیز مقدار پارامتر را مشخص کرده است. خطوط سیاه رنگ چندک‌‌ها و فاصله اطمینان آن‌ها نیز با رنگ خاکستری نشان داده شده. رگرسیون خطی ساده نیز با استفاده از خط قرمز و فاصله اطمینان ۹۵٪ برای پارامتر آن نیز با خط‌چین قرمز در نمودار مشخص است.

مثلا برای صدک پنجم، مقدار عرض از مبدا (Intercept)، تقریبا برابر با 51 است و ضریب متغیر تحصیلات (Education) نیز در این حالت ۱٫۲۲- است. ولی این ضرایب برای چندک ۹۵ام تغییر کرده و به 7۵٫46 برای عرض از مبدا و ۰٫۲۱۹ برای تحصیلات رسیده است.

۴. رگرسیون ستیغی

قبل از بررسی «رگرسیون ستیغی» (Ridge Regression)، بهتر است در مورد «قاعده‌سازی» (Regularization) توضیح دهیم. همانطور که قبلا اشاره شد، بیش‌برازش و کم‌برازش، از مسائلی است که ممکن است که در رگرسیون چندگانه رخ دهد. یکی از راه‌های جلوگیری از این مشکلات، قاعده‌سازی است. به این معنی که مدل رگرسیونی را با توجه به تعداد پارامترهای آن جریمه کرد تا تعداد آن‌ها به یک مقدار بهینه برسد. به این ترتیب پیچیدگی مدل کاهش یافته، بدون آنکه از کارایی آن کاسته شود.

قاعده‌سازی بخصوص در موارد زیر کارساز است:

• تعداد زیاد متغیرهای توصیفی
• زیاد بودن تعداد متغیرها نسبت به تعداد مشاهدات
• هم‌خطی یا هم‌خطی چندگانه در بین متغیرهای توصیفی

در رگرسیون ستیغی از تابع زیان درجه ۲ استفاده می‌شود. به این ترتیب مقدار جریمه (Penalty) برای مدل رگرسیونی، به صورت مجموع مربعات ضرایب مشخص می‌شود.

به این ترتیب اگر مدل رگرسیونی را به صورت زیر در نظر بگیریم:

$$ \large y_{i} = \beta _{0}+\beta _{1}x_{i1} + \cdots +\beta _{p}x_{ip} + \varepsilon _{i} , \qquad i = 1 , \ldots , n $$

مدل رگرسیونی ستیغی به کمک کمینه‌سازی تابع زیر صورت می‌گیرد.

$$ \large \operatorname{argmin} || y – \widehat{y} ||_2^2 = \operatorname{argmin} \sum [y_i – (\beta_0 + \beta_1x_1 + \beta_2x_2 + \cdots + \beta_px_p)]^2 $$

توجه داشته باشید که منظور از  $$\operatorname{argmin}$$ مقدارهایی از $$\beta$$ است که تابع مورد نظر را کمینه می‌کنند.

برای برآورد کردن پارامترهای رگرسیونی در روش ستیغی، قیدی روی پارامترها وجود دارد که به صورت زیر نوشته می‌شود.

$$ \large \beta_0^2 + \beta_1^2 + \cdots + \beta_p^2 \leq C^2 $$

این محدودیت، مشخص می‌کند که باید مجموع مربعات پارامترها از مقدار ثابت یا آستانه‌ای کمتر باشند. به این ترتیب شیوه برآورد پارامترها به صورت زیر در خواهد آمد. مشخص است که بین وجود پارامترهای $$\beta$$ و صفر شدن آن‌ها در بخش قید، توازنی برقرار شده و تعداد پارامترها و متغیرهای مربوطه، بهینه می‌شود.

$$ \large \operatorname{argmin} || y – X \beta ||_2^2 + \lambda || \beta ||_2^2 $$

پارامتر $$\lambda$$ در اینجا میزان جریمه (Regularization Parameter) نامیده می‌شود.

نکته: توجه داشته باشید که قاعده‌سازی فقط برای پارامترهای $$\beta_1$$ تا $$\beta_n$$ صورت می‌گیرد و عرض از مبدا $$\beta_0$$‌ از این موضوع مستثنی است.

برآورد پارامترهای مدل رگرسیون ستیغی با توجه به قیدی که ذکر شده، به صورت زیر خواهد بود.

$$\large \widehat{\beta}^{ridge} =(X^TX+\lambda I)^{-1}X^Ty$$

نکته: مشخص است که اگر هیچ جریمه‌ای برای مدل در نظر نگیریم، به این معنی که مقدار $$\lambda$$ را صفر انتخاب کنیم، روش برآورد در رگرسیون ستیغی به شیوه OLS تبدیل خواهد شد. در نتیجه می‌توان روش OLS را حالت خاصی از روش ستیغی در نظر گرفت.

در تعریف پارامترها در مدل ستیغی، می‌توان دید که مقدار بزرگ برای $$\lambda$$ باعث مشکل کم‌برازش (Underfitting) می‌شود. بنابراین تعیین مقدار صحیح برای لاندا ($$\lambda$$) ضروری است. برای مشخص کردن مقدار مناسب بهتر است نموداری برحسب مقادیر پارامترها و لاندا ترسیم کرد و زمانی که برآوردگرهای ثابتی بوجود آمده‌اند، کوچکترین مقدار لاندا را در نظر گرفت.

برای پیاده‌سازی رگرسیون ستیغی در زبان برنامه‌نویسی R از مجموعه داده سوئیس استفاده کرده و از کتابخانه glment کمک می‌گیریم.

همچنین تابع cv.glmnet نیز با استفاده از اعتبارسنجی متقابل مدل، مقدار مناسب برای لاندا را مشخص می‌کند. حوزه تغییرات لاندا در این مثال $$10^4$$ تا $$10^{-1}$$‌ است که با گام‌های ۰٫۱، کاهش می‌یابد.

library(glmnet)
X = swiss[,-1]
y = swiss[,1]

set.seed(123) #Setting the seed to get similar results.
model = cv.glmnet(as.matrix(X),y,alpha = 0,lambda = 10^seq(4,-1,-0.1))
model
summary(model)

خروجی به صورت زیر خواهد بود.

Call:  cv.glmnet(x = as.matrix(X), y = y, lambda = 10^seq(4, -1, -0.1),      alpha = 0) 
Measure: Mean-Squared Error 
    Lambda Measure     SE Nonzero
min  1.585   63.41  8.941       5
1se  7.943   70.64 12.626       5

           Length Class  Mode     
lambda     51     -none- numeric  
cvm        51     -none- numeric  
cvsd       51     -none- numeric  
cvup       51     -none- numeric  
cvlo       51     -none- numeric  
nzero      51     -none- numeric  
call        5     -none- call     
name        1     -none- character
glmnet.fit 12     elnet  list     
lambda.min  1     -none- numeric  
lambda.1se  1     -none- numeric

به کمک کد زیر، کمترین مقدار لاندا را با lambda.min بدست آورده و مدل مناسب را مشخص می‌کنیم.

best_lambda = model$lambda.min
ridge_coeff = predict(model,s = best_lambda,type = "coefficients")
ridge_coeff

ضرایب حاصل از اجرای مدل رگرسیون ستیغی در این حالت در ادامه دیده می‌شود.

6 x 1 sparse Matrix of class "dgCMatrix"
                           1
(Intercept)      64.92994664
Agriculture      -0.13619967
Examination      -0.31024840
Education        -0.75679979
Catholic          0.08978917
Infant.Mortality  1.09527837

۵. رگرسیون لاسو

اصطلاح لاسو (Lasso) مخفف عبارت (Least Absolute Shrinkage and Selection Operator) یا «عمل‌گر گزینش و انقباض کمترین قدرمطلق» است. در این مدل، نحوه قاعده‌سازی براساس تابع زیان قدر مطلق انجام می‌شود. در نتیجه تابع هدف در «رگرسیون لاسو» (Lasso Regression) به صورت زیر نوشته می‌شود.

$$\sum_{i=1}^n(y_i-\beta_0-\sum_{j=1}^px_{ij}\beta_j)^2+\lambda \sum_j|\beta_j|$$

نکته: در اینجا نیز به مانند رگرسیون ستیغی، فرض نرمال بودن باقی‌مانده‌ها وجود ندارد. همچنین مقدار ثابت یا عرض از مبدا هم در قاعد‌ه‌سازی دخیل نمی‌شود.

نحوه استفاده از رگرسیون لاسو برای داده‌های سوئیس در ادامه دیده می‌شود. همانطور که مشاهده می‌کنید، همه متغیرها به جز ستون اول به عنوان متغیر توصیفی و ستون اول برای متغیر پاسخ در نظر گرفته شده است.

X = swiss[,-1]
y = swiss[,1]

set.seed(123)
model = cv.glmnet(as.matrix(X),y,alpha = 1,lambda = 10^seq(4,-1,-0.1))
#By default standardize = TRUE
set.seed(123)
model = cv.glmnet(as.matrix(X),y,alpha = 1,lambda = 10^seq(4,-1,-0.1))
model
summary(model)

باز هم از cv.glmnet برای استفاده از اعتبارسنجی متقابل برای تعیین مقدار مناسب برای پارامتر لاندا استفاده شده است. توجه داشته باشید که برای استفاده از رگرسیون لاسو، مقادیر متغیرها باید استاندارد (Standardize) شده باشند. به طور پیش‌فرض این کار در تابع cv.glmnet صورت می‌گیرد.

خروجی به صورت زیر ظاهر خواهد شد.

> model
Call:  cv.glmnet(x = as.matrix(X), y = y, lambda = 10^seq(4, -1, -0.1),      alpha = 1) 
Measure: Mean-Squared Error 
    Lambda Measure    SE Nonzero
min 0.1259   66.05  9.00       5
1se 1.5849   74.24 12.53       4
> summary(model)
           Length Class  Mode     
lambda     51     -none- numeric  
cvm        51     -none- numeric  
cvsd       51     -none- numeric  
cvup       51     -none- numeric  
cvlo       51     -none- numeric  
nzero      51     -none- numeric  
call        5     -none- call     
name        1     -none- character
glmnet.fit 12     elnet  list     
lambda.min  1     -none- numeric  
lambda.1se  1     -none- numeric

به منظور پیدا کردن بهترین مقدار لاندا از کد زیر استفاده کرده‌ایم.

best_lambda = model$lambda.min
lasso_coeff = predict(model,s = best_lambda,type = "coefficients")
lasso_coeff

در نتیجه مقادیر ضرایب بر این اساس به صورت زیر درخواهد آمد.

6 x 1 sparse Matrix of class "dgCMatrix"
                           1
(Intercept)      65.46374579
Agriculture      -0.14994107
Examination      -0.24310141
Education        -0.83632674
Catholic          0.09913931
Infant.Mortality  1.07238898

از آنجایی که نتایج حاصل از رگرسیون لاسو با رگرسیون ستیغی نزدیک هستند، سوالی که مطرح می‌شود این است که کدام یک نسبت به دیگری ارجح است؟

همانطور که گفته شد، هر دو روش رگرسیونی، مشکل هم‌خطی یا هم‌خطی چندگانه را حل می‌کنند و مدلی بدون بیش‌برازش یا کم‌برازش ارائه می‌دهند. ولی مدل رگرسیون ستیغی، از لحاظ سرعت محاسباتی، سریعتر است. بهترین راه تشخیص مدل مناسب در بین مدل‌های تولید شده توسط دو روش رگرسیونی، استفاده از اعتبارسنجی متقابل براساس داده‌های آزمایشی است.

۶. رگرسیون شبکه الاستیک

«رگرسیون شبکه الاستیک» (Elastic Net Regression)، با ترکیب رگرسیون لاسو و رگرسیون ستیغی، بر معایب آن‌ها غلبه کرده و جایگزین مطمئن برای آن‌ها است. به این ترتیب اگر با مدلی مواجه هستید که متغیرهای توصیفی آن با یکدیگر همبستگی دارند، بهتر است از رگرسیون شبکه الاستیک استفاده کنید.

به این ترتیب یک قاعده‌سازی مرتبه ۱ و ۲ روی مدل همزمان اعمال می‌شود. در نتیجه تابع هدف در رگرسیون شبکه الاستیک به صورت زیر نوشته خواهد شد.

$$ \large \min(\sum \epsilon^2 + \lambda_1\sum\beta_i+\lambda_2\sum |\beta_i|) $$

که با در نظر گرفتن مدل رگرسیون خطی چندگانه، می‌توان آن را به صورت زیر نیز در نظر گرفت.

$$ \large \min( \sum y_i – ( \beta_0 + \beta_1 X_1 + \beta_2X_2 + \ldots + \beta_kX_k)^2 + \lambda_1 \sum \beta_i^2 + \lambda_2\sum|\beta_i|) $$

توجه داشته باشید که همانند رگرسیون لاسو و رگرسیون ستیغی، فرض نرمال بودن باقی‌مانده در رگرسیون الاستیک نیز وجود ندارد.

فایل داده swiss (سوئیس) را در نظر بگیرید. متغیر پاسخ Y براساس ستون اول این مجموعه داده و بقیه به عنوان متغیر X یا توصیفی در نظر گرفته شده‌اند.

مدل رگرسیونی شبکه الاستیک توسط کدهای زیر در نرم‌افزار R پیاده‌سازی شده است.

library(glmnet)
X = swiss[,-1]
y = swiss[,1]
model = cv.glmnet(as.matrix(X),y,alpha = 0.5,lambda = 10^seq(4,-1,-0.1))
#Taking the best lambda
model
best_lambda = model$lambda.min
en_coeff = predict(model,s = best_lambda,type = "coefficients")
en_coeff

مقادیر alpha و lambda از قبل برای تشکیل مدل در نظر گفته شده‌اند که همان پارامترهای اصلی برای مدل رگرسیون سه تیغی و لاسو هستند. حاصل خروجی به صورت زیر خواهد بود.

> model
Call:  cv.glmnet(x = as.matrix(X), y = y, lambda = 10^seq(4, -1, -0.1),      alpha = 0.5) 

Measure: Mean-Squared Error 

    Lambda Measure    SE Nonzero
min  0.398   64.34 15.02       5
1se  3.981   75.70 18.39       4
> en_coeff
6 x 1 sparse Matrix of class "dgCMatrix"
                           1
(Intercept)      64.05919123
Agriculture      -0.12604667
Examination      -0.25484517
Education        -0.77825368
Catholic          0.09140641
Infant.Mortality  1.07581457

نتایج حاصل از برآورد پارامترهای مدل را با دو شیوه رگرسیون لاسو و ستیغی مقایسه کنید. به نظر می‌رسد که نتیجه برآورد در رگرسیون شبکه الاستیک به آن‌ها بسیار نزدیک است.

۷. رگرسیون مولفه‌های اصلی

زمانی که هم‌خطی یا هم‌خطی چندگانه در مدل رگرسیونی وجود داشته باشد، بهتر است از مدل رگرسیون مولفه‌های اصلی (Principle Component Regression) که به اختصار با PCR نشان داده می‌شود، استفاده کنیم.

رگرسیون مولفه‌های اصلی در دو گام اجرا می‌شود.

1. استخراج مولفه‌های اصلی براساس متغیرهای توصیفی
2. اجرای رگرسیون براساس مولفه‌های ایجاد شده به عنوان متغیرهای مستقل با متغیر پاسخ

به این ترتیب، مشکل هم‌خطی یا هم‌خطی چندگانه از مدل رگرسیونی خارج شده و از طرفی با توجه به استفاده از مولفه‌های کمتر از تعداد متغیرهای توصیفی، ابعاد یا تعداد متغیرهای به کار رفته در مدل رگرسیونی نیز کاهش می‌یابد.

بخش اول در محاسبات مربوط به رگرسیون مولفه‌های اصلی، تعیین «بارهای عاملی» (Loads) است که به کمک آن مولفه‌ها ایجاد می‌شوند. هر مولفه (مثل $$U_i$$) به صورت زیر تشکیل می‌شود.

$$ \large U_i =  \beta_1X_1 + \beta_2X_2 + \ldots + \beta_pX_p $$

با شرط اینکه بارها ($$\beta_i$$) در شرط زیر صدق کنند.

$$ \large \sum_{i=1}^p \beta_i^2 =  1 $$

اولین مولفه اصلی دارای بیشترین سهم از واریانس متغیر پاسخ را در خود جای داده است. به همین ترتیب، مولفه‌های بعدی، سهم کمتری در بیان واریانس کل متغیر پاسخ خواهند داشت.

موضوع دیگری که در مورد مولفه‌های اصلی وجود دارد، ناهمبسته بودن آن‌ها است. به این معنی که ضریب همبستگی بین مولفه‌ها تقریبا صفر است. در نتیجه مشکل هم‌خطی یا هم‌خطی چندگانه در مدل ایجاد شده، از بین خواهد رفت.

همچنین از آنجایی که مقدار $$p$$ را می‌توان کمتر یا مساوی با $$k$$ انتخاب کرد، کاهش بعد مسئله نیز از مزایای استفاده از PCR محسوب می‌شود. در نتیجه می‌توان به جای استفاده از مدل با ۱۰ متغیر توصیفی، فقط با ۲ یا ۳ مولفه، مدل رگرسیونی را ایجاد کرد بطوریکه کمترین میزان اطلاعات در مورد متغیر وابسته، در مدل از بین رفته یا نادیده گرفته شده باشد.

نکته: باید این موضوع را در نظر بگیرم که استفاده از PCR، روشی برای تعیین ویژگی‌های موثر در مدل رگرسیونی نیست بلکه با بهره‌گیری از آن، مولفه‌های جدیدی ایجاد می‌شود که بیشترین توصیف یا سهم تغییرات برای متغیر وابسته را در خود دارند. در نتیجه نمی‌توان گفت که کدام متغیر توصیفی، بیشترین نقش را در مدل رگرسیونی PCR دارد.

به منظور پیاده‌سازی رگرسیون PCR از کتابخانه pls در زبان برنامه‌نویسی و محاسباتی R استفاده می‌کنیم. پس ابتدا کتابخانه‌ را نصب و سپس بارگذاری می‌کنیم.

install.packages("pls")
library(pls)

در اینجا از مجموعه داده longley استفاده می‌کنیم که در R به طور پیش‌فرض وجود دارد. به جز ستون سال (Year) بقیه متغیرها را استفاده خواهیم کرد.

data1 = longley[,colnames(longley) != "Year"]
View(data1)

در ادامه این داده‌ها را مشاهده می‌کنید. قرار است تعداد افراد شاغل (Employed) را براساس متغیرهای دیگر نظیر «جمعیت» (Population)، «نیروی نظامی» (Armed.Forces)، «تعداد افراد بیکار» (Unemployed)، «شاخص درآمد ناخالص ملی» (GNP) و «شاخص درآمد ضمنی ناخالص ملی» (GNP.deflator)، مدل‌سازی کنیم.

> longley
     GNP.deflator     GNP Unemployed Armed.Forces Population Year Employed
1947         83.0 234.289      235.6        159.0    107.608 1947   60.323
1948         88.5 259.426      232.5        145.6    108.632 1948   61.122
1949         88.2 258.054      368.2        161.6    109.773 1949   60.171
1950         89.5 284.599      335.1        165.0    110.929 1950   61.187
1951         96.2 328.975      209.9        309.9    112.075 1951   63.221
1952         98.1 346.999      193.2        359.4    113.270 1952   63.639
1953         99.0 365.385      187.0        354.7    115.094 1953   64.989
1954        100.0 363.112      357.8        335.0    116.219 1954   63.761
1955        101.2 397.469      290.4        304.8    117.388 1955   66.019
1956        104.6 419.180      282.2        285.7    118.734 1956   67.857
1957        108.4 442.769      293.6        279.8    120.445 1957   68.169
1958        110.8 444.546      468.1        263.7    121.950 1958   66.513
1959        112.6 482.704      381.3        255.2    123.366 1959   68.655
1960        114.2 502.601      393.1        251.4    125.368 1960   69.564
1961        115.7 518.173      480.6        257.2    127.852 1961   69.331
1962        116.9 554.894      400.7        282.7    130.081 1962   70.551

اگر دسترسی به این مجموعه داده برایتان مقدور نیست، می‌توانید فایل longley را از اینجا با قالب فشرده از اینجا دریافت کنید و پس از خارج کردن از حالت فشرده با دستور read.csv در R‌ بارگذاری کنید.

از آنجایی که بعضی از این متغیرها به یکدیگر وابستگی دارند (مثلا درآمد ناخالص ملی با تعداد افراد بیکار و همچنین درآمد ضمنی ناخالص ملی در رابطه است)، بهتر است از مدل PCR استفاده کنیم. کد زیر به این منظور نوشته شده است. همانطور که مشاهده می‌کنید، مدل ~.Employed نشانگر ارتباط بین متغیر Employed با بقیه متغیرها است.

pcr_model <- pcr(Employed~., data = data1, scale = TRUE, validation = "CV")
summary(pcr_model)

خروجی به صورت زیر خواهد بود.

Data:  X dimension: 16 5 
 Y dimension: 16 1
Fit method: svdpc
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept)  1 comps  2 comps  3 comps  4 comps  5 comps
CV           3.627    1.194    1.118   0.5555   0.6514   0.5954
adjCV        3.627    1.186    1.111   0.5489   0.6381   0.5819

TRAINING: % variance explained
          1 comps  2 comps  3 comps  4 comps  5 comps
X           72.19    95.70    99.68    99.98   100.00
Employed    90.42    91.89    98.32    98.33    98.74

همانطور که مشاهده می‌کنید، حدود 95٫70 درصد تغییرات متغیر وابسته توسط دو مولفه اول و دوم در مدل رگرسیونی PCR پوشش داده می‌شوند. به عنوان شاخص برای اعتبار مدل از RMSEP یا «ریشه میانگین مربعات خطای پیش‌بینی» (Root Mean Square Error Of Prediction) استفاده شده است. همچنین محاسبه اعتبارسنجی متقابل (Crossvalidation) برای سنجش کارایی مدل روی داده‌ها براساس هر یک از مدل‌ها (تعداد مولفه‌ها) صورت گرفته است.

کد زیر به منظور ترسیم نمودار اعتبار سنجی نوشته شده است. همچنین در انتها نیز مقادیر پیش‌بینی شده براساس سه مولفه، محاسبه شده‌اند.

validationplot(pcr_model,val.type = "MSEP")

validationplot(pcr_model,val.type = "R2")

pred = predict(pcr_model,data1,ncomp = 3)

خروجی به صورت زیر خواهد بود.

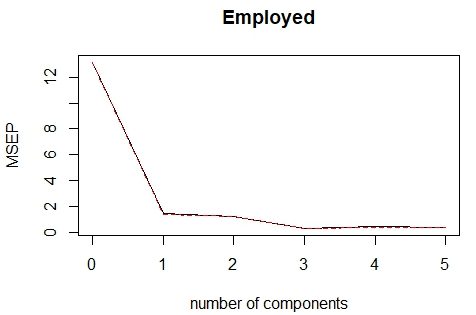
همانطور که مشخص است با افزایش تعداد مولفه‌ها، میزان خطای MSEP نیز کاهش می‌یابد ولی از مولفه سوم به بعد این کاهش خیلی محسوس نیست و می‌توان براساس سه مولفه اول کار محاسبات و ایجاد مدل رگرسیونی را انجام داد.

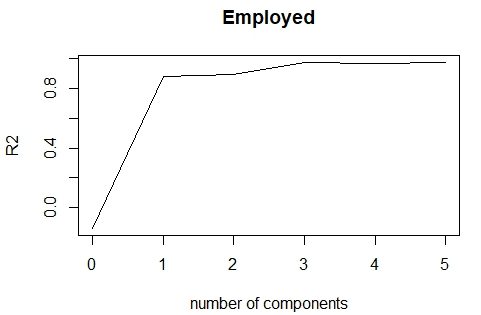
از طرفی نمودار $$R^2$$ نیز نشان می‌دهد که با افزایش تعداد مولفه‌ها، ضریب تعیین افزایش داشته ولی از مولفه سوم به بعد باز هم تغییرات آن چشمگیر نیست. بنابراین اگر سه مولفه اول در مدل به کار گرفته شوند، بهترین دقت و کمترین خطا را به همراه کمترین تعداد مولفه‌ها خواهیم داشت.

حاصل پیش‌بینی‌ها توسط این سه مولفه در ادامه قابل مشاهده است.

> pred
, , 3 comps

     Employed
1947 60.14949
1948 61.52509
1949 60.14052
1950 61.28339
1951 63.57905
1952 64.23811
1953 65.08944
1954 63.66381
1955 65.47474
1956 66.68995
1957 67.77152
1958 66.59554
1959 68.67805
1960 69.47458
1961 69.41667
1962 71.30205

همچنین اگر پیش‌بینی را براساس هر یک از مولفه‌ها جداگانه محاسبه و نمودار آن را رسم کنیم، مشخص می‌شود که تفاوت زیادی بین مولفه‌ها در پیش‌بینی وجود ندارد.

firstcomp1=pcr_model$fitted.values[,,1]
firstcomp2=pcr_model$fitted.values[,,2]
firstcomp3=pcr_model$fitted.values[,,3]

plot(firstcomp1,data1$Employed,col=1,xlab="Comp Values",ylab="Real Value")
lines(firstcomp2,data1$Employed,type='p',col=5)
lines(firstcomp3,data1$Employed,type='p',col=2)
legend(60,70,legend=c("comp1","comp2","comp3"),col=c(1,5,2),lty=1)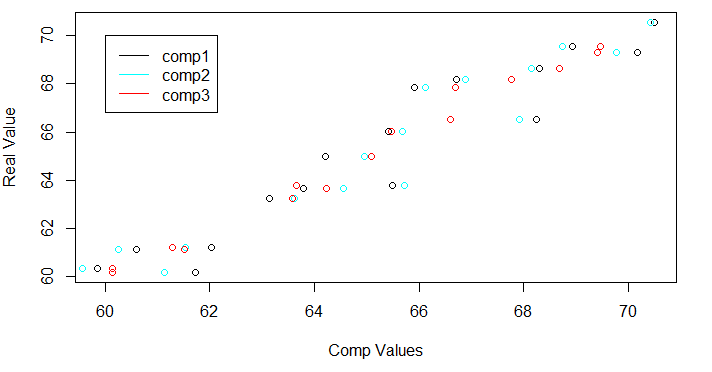

۸. رگرسیون کمترین مربعات جزئی

زمانی که بین متغیرهای توصیفی، وابستگی شدید وجود داشته باشد، به جای رگرسیون مولفه‌های اصلی (PCR) بهتر است از رگرسیون کمترین مربعات جزئی (PLS) یا Partial Least Square Regression استفاده شود. همچنین زمانی که تعداد متغیرهای توصیفی زیاد هستند و می‌خواهیم موثرترین متغیرها در مدل حضور داشته باشند، از رگرسیون کمترین مربعات جزئی (PLS) استفاده می‌کنیم.

هم در روش رگرسیون مولفه‌های اصلی و هم کمترین مربعات جزئی، متغیر جدیدی به عنوان متغیر پیش‌گو ساخته می‌شود که به آن مولفه (Component) گفته می‌شود. این متغیر جدید، ترکیب خطی از متغیرهای توصیفی است. ولی تفاوت در این است که در تحلیل رگرسیون PCR، مولفه‌ها براساس توصیف واریانس کل متغیرهای توصیفی (پیشگو-Predictor) تولید می‌شوند بدون آنکه به مقایر متغیر پاسخ توجه شود. در حالیکه در PLS با در نظر گرفتن متغیر پاسخ و متغیرهای پیشگو، مولفه‌ها تولید می‌شوند و در نهایت مدلی ایجاد می‌شود که با کمترین عوامل، بهترین برازش را دارد.

در کد زیر براساس مجموعه داده vehicles که مشخصات خودروها را ثبت کرده، می‌خواهیم قیمت خودرو (ستون سیزدهم) با نام متغیر price را برحسب متغیرهای دیگر مدل‌بندی کنیم. به منظور دسترسی به این مجموعه داده می‌توانید فایل vehicles را از اینجا به قالب فشرده دریافت کنید و پس از خارج کردن از حالت فشرده، به کمک دستور read.csv آن را در در برنامه R فراخوانی و بارگذاری کنید.

ابتدا بعضی از مقادیر این مجموعه داده را نمایش می‌دهیم. این مجموعه داده، شامل 30 مشاهده و 16 متغیر است. برای ایجاد مدل رگرسیونی PLS از متغیر سیزدهم یعنی قیمت خودرو (price) به عنوان متغیر وابسته استفاده می‌کنیم. همچنین بقیه متغیرها به عنوان متغیرهای پیشگو به کار خواهند رفت.

> head(vehicles)
          diesel turbo two.doors hatchback wheel.base length width height curb.weight eng.size
alfaromeo      0     0         1         1       94.5  171.2  65.5   52.4        2823      152
audi           0     0         0         0      105.8  192.7  71.4   55.7        2844      136
bmw            0     0         1         0      101.2  176.8  64.8   54.3        2395      108
chevrolet      0     0         0         0       94.5  158.8  63.6   52.0        1909       90
dodge1         0     1         1         1       93.7  157.3  63.8   50.8        2128       98
dodge2         0     0         0         1       93.7  157.3  63.8   50.6        1967       90
          horsepower peak.rpm price symbol city.mpg highway.mpg
alfaromeo        154     5000 16500      1       19          26
audi             110     5500 17710      1       19          25
bmw              101     5800 16430      2       23          29
chevrolet         70     5400  6575      0       38          43
dodge1           102     5500  7957      1       24          30
dodge2            68     5500  6229      1       31          38

توجه داشته باشید که برای اجرای رگرسیون PLS باید از کتابخانه plsdepot استفاده کنید. مجموعه داده vehicles نیز در این کتابخانه قرار دارد.

library(plsdepot)
data(vehicles)
pls.model = plsreg1(vehicles[, c(1:12,14:16)], vehicles[, 13], comps = 3)
# summary
summary(pls.model)
# Predicted values
pls.model$y.pred
# loads of factors
pls.model$x.loads
# R-Square
pls.model$R2

همانطور که مشاهده می‌کنید، رگرسیون PLS‌ از سه مولفه استفاده کرده است زیرا در کد عبارت comps=3 به کار رفته است. به این ترتیب خروجی به صورت زیر خواهد بود.

> summary(pls.model)
          Length Class  Mode   
x.scores  90     -none- numeric
x.loads   45     -none- numeric
y.scores  90     -none- numeric
y.loads    3     -none- numeric
cor.xyt   48     -none- numeric
raw.wgs   45     -none- numeric
mod.wgs   45     -none- numeric
std.coefs 15     -none- numeric
reg.coefs 16     -none- numeric
R2         3     -none- numeric
R2Xy      48     -none- numeric
y.pred    30     -none- numeric
resid     30     -none- numeric
T2        93     -none- numeric
Q2        15     -none- numeric
y         30     -none- numeric
> # Predicted values
> pls.model$y.pred
         1          2          3          4          5          6          7          8          9 
18186.8186 17880.1674 14547.1022  5990.3904  8805.9785  4357.6998  5545.7037 10140.0942  7306.1875 
        10         11         12         13         14         15         16         17         18 
36512.4736  5221.2953 25798.8095 17472.6262  6653.6606  6809.4727  6977.2829  4357.6998 17427.1386 
        19         20         21         22         23         24         25         26         27 
33931.7662 14254.0017  8285.7662   784.7039 10960.9806 15410.8928 10749.3651 11546.7997 14782.5522 
        28         29         30 
13053.9396 18398.4627 19615.1680 
> # loads of factors
> pls.model$x.loads
                     p1         p2           p3
diesel       0.09271495 -0.3890200  0.678689303
turbo        0.18536097 -0.2436168 -0.086493899
two.doors   -0.10124057  0.3717346 -0.039073060
hatchback   -0.14373397  0.2481944 -0.480716370
wheel.base   0.32361239 -0.2729353 -0.018798612
length       0.35328772 -0.1794076  0.022031790
width        0.33579957 -0.1300531  0.008125624
height       0.20723718 -0.3762250 -0.099462195
curb.weight  0.37681297 -0.0261901  0.117117365
eng.size     0.34243554  0.1890635  0.252856936
horsepower   0.29507625  0.3616392 -0.081524076
peak.rpm    -0.11417298  0.3743210 -0.273045978
symbol      -0.14375163  0.4326949  0.131893643
city.mpg    -0.31971248 -0.2441165  0.352607126
highway.mpg -0.34605016 -0.1329582  0.317595249
> # R-Square
> pls.model$R2
        t1         t2         t3 
0.70474894 0.11708109 0.09872169

در بخش اول، متغیرها و مقادیرشان معرفی شده‌اند. در بخش دوم، مقدارهای پیش‌بینی شده توسط مدل برای متغیر وابسته با دستور pls.model$y.pred ظاهر شده است. همچنین بارهای عاملی برای تشکیل مولفه‌ها، براساس سه مولفه اول مشخص شده. به این ترتیب ضریب هر یک از متغیرهای توصیفی که در اینجا همان عامل‌ها نامیده می‌شوند، در تشکیل مدل رگرسیونی، دیده می‌شوند.

در انتها نیز ضریب $$R^2$$ برای هر یک از مولفه‌ها مشخص شده است. همانطور که انتظار داریم، اولین مولفه، بیشترین همبستگی را با متغیر وابسته دارد. به همین ترتیب برای مولفه‌های دوم و سوم، ضریب همبستگی کاهش یافته است.

۹. رگرسیون بردار پشتیبان

به کمک رگرسیون بردار پشتیبان (Support Vector Regression)  که گاهی آن را با SVR نیز نشان می‌دهند، می‌توان مدل‌های خطی و غیرخطی را ایجاد و پارامترهای آن را محاسبه کرد. این کار توسط به کارگیری یک «تابع هسته» (kernel) غیرخطی (مانند چندجمله‌ای) حاصل می‌شود. محاسبه پارامترهای این تابع به شکل است که خطا کمینه شود بطوری که فاصله بین صفحاتی که عمل جداسازی بین دسته‌ها را ایجاد می‌کنند، بیشینه شود.

کتابخانه e1071 از زبان برنامه‌نویسی R، امکان اجرای رگرسیون بردار پشتیبان را می‌دهد. در کدی که در ادامه مشاهده می‌کنید، با استفاده از داده‌های شبیه‌سازی شده، یک مدل رگرسیونی بردار پشتیبان ایجاد می‌شود.

متغیر مستقل (x) براساس دنباله‌ای از مقادیر ۰ تا ۵ با افزایش ۰٫۰۵ تولید شده است. متغیر وابسته (y) نیز براساس رابطه زیر ساخته شده است.

$$ \large y = \log(x) + z, \; \; \; z \sim N(mean = x , standard deviation = 0.2) $$

پارامترها و کد دستوری برای اجرای این مدل رگرسیونی در ادامه قابل مشاهده است.

svm.default(x = x, y = y)
Parameters:
   SVM-Type:  eps-regression 
 SVM-Kernel:  radial 
       cost:  1 
      gamma:  1 
    epsilon:  0.1 

Number of Support Vectors:  71

کدی که در ادامه مشاهده می‌کنید، برای اجرای رگرسیون SVM برای داده‌های شبیه‌سازی شده به کار می‌رود.  پس از اجرای مدل، مقادیر پیش‌بینی شده نیز محاسبه شده و به همراه مقادیر x و y در یک نمودار ترسیم می‌شود.

library(e1071)
# create data
x <- seq(0.1, 5, by = 0.05)
y <- log(x) + rnorm(x, sd = 0.2)

# estimate model and predict input values
m   <- svm(x, y)
new <- predict(m, x)

# visualize
plot(x, y)
points(x, log(x), col = 2)
points(x, new, col = 4)

همانطور که مشخص است مدل رگرسیون حاصل، غیرخطی بوده و توانسته است داده‌ها را به خوبی پیش‌بینی کند. نتیجه خروجی و نمودار حاصل در ادامه قابل مشاهده است.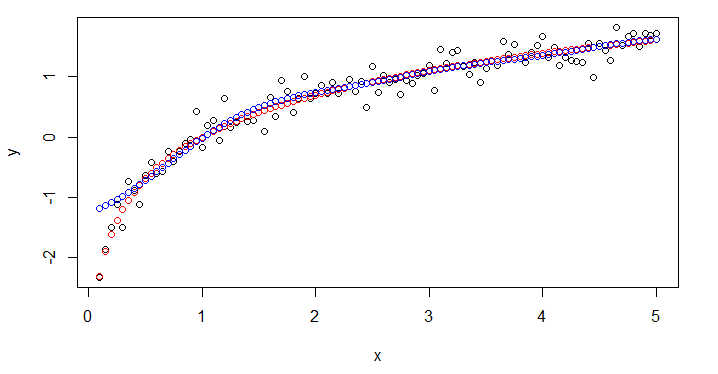

نقطه‌های مشکی رنگ، بیانگر نقاط x و y است. نقطه‌های قرمز رنگ هم نتیجه ارتباط بین نقاط x با (log(x را نشان می‌دهد. قرار است ارتباط بین y با (log(x را به صورت خطی نمایش دهیم. مدل برازش شده توسط رگرسیون SVM نیز با نقطه‌های آبی رنگ روی نمودار دیده می‌شود که انطباق مناسبی با نقطه‌های قرمز رنگ دارد. البته در مقادیر نزدیک به صفر این مطابقت از بین رفته است زیرا تغییرات لگاریتم در این قسمت شدید خواهد بود.

۱۰. رگرسیون ترتیبی

اگر متغیر پاسخ یا وابسته به صورت ترتیبی (Ordinal) یا رتبه‌ای (Rank) باشد، بهتر است از مدل رگرسیون ترتیبی (Ordinal Regression) استفاده شود. به این ترتیب اگر با استفاده از طیف لیکرت (Likert Scale)، با پاسخ‌های مربوط به پرسشنامه مواجه هستید، بهتر است برای مدل‌سازی بین این متغیر پاسخ با متغیرهای مستقل یا توصیفی، از رگرسیون ترتیبی استفاده کنید. برای مثال ممکن است براساس یک پرسش‌نامه که پاسخ‌های آن با مقیاس یا طیف لیکرت ۵ سطحی تشکیل شده بخواهید میزان بهبود درد بیماران نسبت به دوزهای مختلف یک دارو را بسنجید. چنین مدلی به کمک رگرسیون ترتیبی ساخته خواهد شد.

به منظور پیاده‌سازی این مدل از رگرسیون با مجموعه داده wine که میزان تندی سرکه را مشخص کرده است کار خواهیم کرد. این مجموعه داده، شامل ۷۲ مشاهده است که براساس قضاوت ۹ داور میزان تندی با متغیر رتبه‌ای response از ۰ تا ۱۰۰ مشخص و درجه‌بندی شده است. همچنین متغیر rating نیز مقادیر response را به ۵ طبقه به صورت ترتیبی، گروه‌بندی کرده است. دما (temp) با دو سطح گرم و سرد و همچنین نحوه چیدن انگور با متغیر contact با دوسطح no و yes ثبت شده. نوع بطری (bottle) نیز نحوه نگهداری سرکه را با توجه به هشت وضعیت مختلف تعیین می‌کند.

ابتدا به مجموعه داده، نگاه مختصری می‌کنیم. اگر به این داده‌ها دسترسی ندارید می‌توانید فایل اطلاعاتی مربوط به آن را از اینجا دریافت و پس از خارج کردن از حالت فشرده، در R با دستور read.csv بارگذاری کنید.

> head(wine)
  response rating temp contact bottle judge
1       36      2 cold      no      1     1
2       48      3 cold      no      2     1
3       47      3 cold     yes      3     1
4       67      4 cold     yes      4     1
5       77      4 warm      no      5     1
6       60      4 warm      no      6     1

در اینجا، مدل ارائه شده طبق کد زیر به بررسی رابطه بین متغیر وابسته rating به عنوان متغیر عامل یا ترتیبی با داورها (judge) و دما (temp) پرداخته‌ایم.

library(ordinal)
o.model <- clm( rating~ temp*judge, data = wine)
summary(o.model)

خروجی به صورت زیر خواهد بود.

formula: rating ~ temp * judge
data:    wine

 link  threshold nobs logLik AIC    niter max.grad cond.H 
 logit flexible  72   -73.79 189.58 6(0)  3.99e-07 4.7e+02

Coefficients:
                  Estimate Std. Error z value Pr(>|z|)   
tempwarm         3.683e+00  1.465e+00   2.514  0.01194 * 
judge2          -4.132e+00  1.643e+00  -2.515  0.01189 * 
judge3          -1.357e+00  1.360e+00  -0.998  0.31838   
judge4          -1.357e+00  1.360e+00  -0.998  0.31838   
judge5          -3.433e-16  1.390e+00   0.000  1.00000   
judge6          -1.357e+00  1.360e+00  -0.998  0.31838   
judge7          -4.720e+00  1.579e+00  -2.990  0.00279 **
judge8          -2.152e+00  1.403e+00  -1.534  0.12495   
judge9          -2.995e+00  1.549e+00  -1.933  0.05320 . 
tempwarm:judge2  1.703e+00  2.218e+00   0.768  0.44259   
tempwarm:judge3  1.357e+00  1.893e+00   0.717  0.47359   
tempwarm:judge4 -2.086e+00  2.022e+00  -1.031  0.30240   
tempwarm:judge5 -3.663e+00  1.970e+00  -1.859  0.06301 . 
tempwarm:judge6 -1.402e-01  1.950e+00  -0.072  0.94269   
tempwarm:judge7 -3.202e-01  2.094e+00  -0.153  0.87850   
tempwarm:judge8 -8.934e-01  1.956e+00  -0.457  0.64786   
tempwarm:judge9  1.057e-01  2.102e+00   0.050  0.95990   
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Threshold coefficients:
    Estimate Std. Error z value
1|2   -4.656      1.271  -3.663
2|3   -1.302      1.013  -1.285
3|4    1.341      1.013   1.325
4|5    3.507      1.171   2.994

۱۱. رگرسیون پواسون

زمانی که متغیر وابسته به صورت شمارشی باشد، از مدل رگرسیون پواسون (Poisson Regression) استفاده می‌کنیم. به عنوان مثال در پیش‌بینی تعداد تماس‌های تلفن در یک شرکت برحسب میزان فروش یا برآورد تعداد تماس‌های به بخش اورژانس بر اساس رخداد یک سانحه! همچنین تعداد مرگ و میر بر اثر عوامل آلودگی هوا از مدل رگرسیون پواسن استفاده می‌شود.

متغیر وابسته در این مدل باید شرایط زیر را داشته باشد:

1. متغیر وابسته (y) دارای توزیع پواسون است.
2. مقدار متغیر وابسته نباید منفی باشد (زیرا حاصل از شمارش است).
3. مدل رگرسیون پواسن برای زمانی که مقادیر متغیر وابسته متعلق به مجموعه اعداد طبیعی نیستند، نباید استفاده شود.

به منظور اجرای مدل رگرسیون پواسون از یک مجموعه داده که مربوط به پارگی دو نوع نخ است استفاده می‌کنیم. ابتدا به داده‌های warpbreaks نگاهی می‌اندازیم. این مجموعه داده شامل ۵۴ مشاهده و ۳ متغیر است.

• تعداد پارگی‌ها (breaks) که مقادیر آن به صورت شمارشی است.
• نوع نخ (wool) که با دو مقدار A و B‌ مشخص شده است.
• میزان کشش (tension) که در سه سطح کم (L)، متوسط (M) و زیاد (H) طبقه‌بندی شده است.

اگر از طریق برنامه R به این مجموعه داده دسترسی ندارید می‌توانید فایل مربوطه را با قالب فشرده از اینجا دریافت کنید. پس از خارج کردن فایل از حالت فشرده با دستور read.csv آن را بارگذاری کنید.

> head(warpbreaks)
  breaks wool tension
1     26    A       L
2     30    A       L
3     54    A       L
4     25    A       L
5     70    A       L
6     52    A       L

کدی که در ادامه مشاهده می‌کنید، مربوط به مجموعه داده استحکام نخ‌ها است. تعداد پارگی‌های نخ‌ها (breaks) برحسب نوع نخ (wool)، کشش نخ (tension) و اثر متقابل این دو براساس یک مدل رگرسیونی پواسون، مورد محاسبه قرار گرفته و پارامترهای آن بدست آمده است.

pos.model<-glm(breaks~wool*tension, data = warpbreaks, family=poisson)
summary(pos.model)

از آنجایی که در مدل عبارت wool*tension دیده می‌شود، اثرات اصلی و متقابل بین این دو متغیر در مدل نیز حضور خواهند داشت. خروجی به صورت زیر خواهد بود.

glm(formula = breaks ~ wool * tension, family = poisson, data = warpbreaks)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.3383  -1.4844  -0.1291   1.1725   3.5153  

Coefficients:
               Estimate Std. Error z value Pr(>|z|)    
(Intercept)     3.79674    0.04994  76.030  < 2e-16 ***
woolB          -0.45663    0.08019  -5.694 1.24e-08 ***
tensionM       -0.61868    0.08440  -7.330 2.30e-13 ***
tensionH       -0.59580    0.08378  -7.112 1.15e-12 ***
woolB:tensionM  0.63818    0.12215   5.224 1.75e-07 ***
woolB:tensionH  0.18836    0.12990   1.450    0.147    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for poisson family taken to be 1)

    Null deviance: 297.37  on 53  degrees of freedom
Residual deviance: 182.31  on 48  degrees of freedom
AIC: 468.97

Number of Fisher Scoring iterations: 4

همانطور که مشخص است همه متغیرها (یا ضرایب) در مدل از لحاظ آماری معنی‌دار بوده و فقط نوع نخ B با میزان کشش سطح H در سطح آزمون ۵٪ معنی‌دار نیستند.

از طرفی دیده می‌شود که میانگین مقدار متغیر پاسخ (Intercept) برابر با 3٫79674 است در حالیکه مقدار پراکندگی (Dispersion) برای توزیع پواسن عدد ۱ در نظر گرفته شده است. در نتیجه با مشکل «کم‌پراکنش» (Underdispersion) مواجه هستیم و بهتر است با مدل رگرسیون دوجمله‌ای منفی یا شبه پواسن مدل را ایجاد کنیم. این مدل در ادامه معرفی و به کار گرفته شده است.

۱۲. رگرسیون دوجمله‌ای منفی

برای فراگیری رگرسیون دو جمله‌ای منفی (Negative Binomial Regression) و دستورات مرتبط با آن در R به بررسی یک مجموعه داده به نام quine‌ می‌پردازیم که مربوط به تعداد روزهای غیبت دانش‌آموزان با توجه به قومیت، سن، جنس و سرعت یادگیری آن‌ها است.

این مجموعه داده شامل 146 مشاهده و ۵ متغیر است که از بین مدارس چهار منطقه متفاوت جمع‌آوری شده است.

1. قومیت (Eth) که شامل دو مقدار بومی (A) و غیربومی (N) است.
2. جنسیت (Sex) که شامل دو مقدار دختر (F) و پسر (M) است.
3. سن (Age) که به طبقه‌های F0 تا F3 تقسیم‌بندی شده است.
4. سرعت یادگیری (Lrn) که شامل دو سطح متوسط (AL) و کند (SL) می‌شود.
5. تعداد روزهای غیبت در مدرسه در طول سال (Days) که یک متغیر شمارشی است و به عنوان متغیر وابسته به کار رفته است.

برای دسترسی به این مجموعه داده باید ابتدا کتابخانه MASS را راه‌اندازی کنید. در ادامه قسمتی از اطلاعات این مجموعه داده را مشاهده می‌کنید. اگر به این مجموعه داده دسترسی ندارید، می‌توانید فایل مرتبط با این اطلاعات را از اینجا به صورت یک فایل فشرده دریافت کنید. پس از خارج کردن این فایل از حالت فشرده با دستور read.csv محتویات فایل باز شده را در R فراخوانی کنید.

library(MASS)
> head(quine)
  Eth Sex Age Lrn Days
1   A   M  F0  SL    2
2   A   M  F0  SL   11
3   A   M  F0  SL   14
4   A   M  F0  AL    5
5   A   M  F0  AL    5
6   A   M  F0  AL   13

قرار است به کمک متغیرهای توصیفی که در ستون های اول تا چهارم قرار دارند، مدلی برای پیش‌بینی متغیر پنجم یعنی تعداد روزهای غیبت در مدرسه (Days)، ایجاد کنیم. کد زیر به این منظور نوشته شده است.

nb.model <- glm.nb(Days ~ Sex/(Age + Eth*Lrn), data = quine)
summary(nb.model)

همانطور که مشاهده می‌کنید در اینجا از تابع glm.nb استفاده کرده‌ایم تا مدل رگرسیون دوجمله‌ای منفی را به کار ببریم. در اینجا متغیر وابسته Days و متغیرهای مستقل Sex, Age, Eth و Lrn هستند که البته از متغیر Sex برای تفکیک مدل‌ها استفاده شده است.

خروجی به صورت زیر خواهد بود.

glm.nb(formula = Days ~ Sex/(Age + Eth * Lrn), data = quine, 
    init.theta = 1.597990733, link = log)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.8950  -0.8827  -0.2299   0.5669   2.1071  

Coefficients:
                Estimate Std. Error z value Pr(>|z|)    
(Intercept)      3.01919    0.29706  10.163  < 2e-16 ***
SexM            -0.47541    0.39550  -1.202 0.229355    
SexF:AgeF1      -0.70887    0.32321  -2.193 0.028290 *  
SexM:AgeF1      -0.72373    0.33048  -2.190 0.028527 *  
SexF:AgeF2      -0.61486    0.37141  -1.655 0.097826 .  
SexM:AgeF2       0.62842    0.27366   2.296 0.021655 *  
SexF:AgeF3      -0.34235    0.32717  -1.046 0.295388    
SexM:AgeF3       1.15084    0.31385   3.667 0.000246 ***
SexF:EthN       -0.07312    0.26539  -0.276 0.782908    
SexM:EthN       -0.67899    0.25631  -2.649 0.008072 ** 
SexF:LrnSL       0.94358    0.32246   2.926 0.003432 ** 
SexM:LrnSL       0.23891    0.33553   0.712 0.476443    
SexF:EthN:LrnSL -1.35849    0.37719  -3.602 0.000316 ***
SexM:EthN:LrnSL  0.76142    0.44134   1.725 0.084483 .  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for Negative Binomial(1.598) family taken to be 1)

    Null deviance: 234.56  on 145  degrees of freedom
Residual deviance: 167.56  on 132  degrees of freedom
AIC: 1093

Number of Fisher Scoring iterations: 1


              Theta:  1.598 
          Std. Err.:  0.213 

 2 x log-likelihood:  -1063.025

همانطور که مشاهده می‌کنید برای هر متغیر مستقل، در دو وضعیت پسر و دختر (M و F)، ضرایب به طور مجزا محاسبه شده‌اند. توجه داشته باشید که عرض از مبدا (Intercept) برای گروه دخترها محاسبه شده. برای پسر‌ها باید مقدار محاسبه شده در ضریب SexM به مقدار Intercept اضافه شده تا عرض از مبدا برای مدل رگرسیون دوجمله‌ای منفی در گروه پسرها، حاصل شود.

نکته: همانطور که به یاد دارید، در مدل رگرسیون پواسون، ممکن است با مشکل بیش‌پراکندگی یا کم‌پراکندگی مواجه شویم. در قسمت قبل براساس داده‌های مربوط به کشش نخ‌ها با مشکل کم‌برازش مواجه شدیم. این بار با استفاده از رگرسیون دوجمله‌ای منفی مدل را ایجاد می‌کنیم زیرا نسبت به بیش‌برازش و کم‌برازش مقاوم است. کافی است کد زیر را به کار ببریم.

pos.model<-glm(breaks~wool*tension, data = warpbreaks, family=quasipoisson)
summary(pos.model

خروجی به صورت زیر خواهد بود.

glm(formula = breaks ~ wool * tension, family = quasipoisson, 
    data = warpbreaks)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-3.3383  -1.4844  -0.1291   1.1725   3.5153  

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)     3.79674    0.09688  39.189  < 2e-16 ***
woolB          -0.45663    0.15558  -2.935 0.005105 ** 
tensionM       -0.61868    0.16374  -3.778 0.000436 ***
tensionH       -0.59580    0.16253  -3.666 0.000616 ***
woolB:tensionM  0.63818    0.23699   2.693 0.009727 ** 
woolB:tensionH  0.18836    0.25201   0.747 0.458436    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for quasipoisson family taken to be 3.76389)

    Null deviance: 297.37  on 53  degrees of freedom
Residual deviance: 182.31  on 48  degrees of freedom
AIC: NA

Number of Fisher Scoring iterations: 4

همانطور که مشاهده می‌کنید در قسمت Dispersion parameter، مقدار واریانس 3٫76389 محاسبه شده که با میانگین مدل (Intercept) با مقدار 3٫79674 تقریبا برابر است و مشکل بیش‌پراکندگی یا کم‌پراکندگی بوجود نیامده است.

۱۳. رگرسیون شبه پواسون

یکی از روش‌های رگرسیونی که می‌تواند به عنوان جایگزین رگرسیون دوجمله‌ای منفی به کار رود، رگرسیون شبه پواسون (Quasi Poisson Regression) است. هر چند هر دو شیوه پاسخ‌های یکسانی تولید می‌کنند ولی در ماتریس کوواریانس برآوردگرها اختلافاتی وجود دارد. بطوری که واریانس مدل شبه پواسن، یک ترکیب خطی از میانگین بوده ولی واریانس مدل رگرسیون دو جمله‌ای منفی، به صورت تابعی درجه چهار از میانگین است.

به منظور پیاده‌سازی این مدل رگرسیونی در زبان برنامه‌نویسی R باز هم از تابع glm‌ استفاده می‌کنیم ولی مدل را در قسمت Family برابر با quasipoisson قرار می‌دهیم. مجموعه داده به کار رفته همان quine است که در رگرسیون دو جمله‌ای منفی به کار بردیم.

qs.pos.model <- glm(Days ~ Sex/(Age + Eth*Lrn), data = quine, family = "quasipoisson")

در کد بالا، مدل رگرسیون شبه پواسن را براساس متغیرهای وابسته و مستقل به شکل زیر اجرا کرده‌ایم.

اثر متغیرهای طبقه‌ای سن، به همراه اثرات اصلی (Main Effect) و اثرات متقابل (Interaction) بین متغیرهای قومیت (Eth) و سرعت یادگیری (Lrn) به تفکیک جنسیت (Sex) برای متغیر روز‌های غیبت (Days) مدل‌سازی شده است.

glm(formula = Days ~ Sex/(Age + Eth * Lrn), family = "quasipoisson", 
    data = quine)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-7.3924  -2.4923  -0.5745   1.5507   8.5631  

Coefficients:
                Estimate Std. Error t value Pr(>|t|)    
(Intercept)      2.89964    0.28113  10.314  < 2e-16 ***
SexM            -0.39728    0.38999  -1.019 0.310204    
SexF:AgeF1      -0.48941    0.31188  -1.569 0.118988    
SexM:AgeF1      -0.82267    0.40664  -2.023 0.045081 *  
SexF:AgeF2      -0.19579    0.34387  -0.569 0.570071    
SexM:AgeF2       0.62626    0.26615   2.353 0.020096 *  
SexF:AgeF3      -0.21627    0.31725  -0.682 0.496619    
SexM:AgeF3       1.01691    0.30175   3.370 0.000986 ***
SexF:EthN       -0.08595    0.27661  -0.311 0.756503    
SexM:EthN       -0.49065    0.24160  -2.031 0.044278 *  
SexF:LrnSL       0.73625    0.30990   2.376 0.018950 *  
SexM:LrnSL       0.33779    0.29888   1.130 0.260451    
SexF:EthN:LrnSL -1.27702    0.41039  -3.112 0.002280 ** 
SexM:EthN:LrnSL  0.59021    0.40165   1.469 0.144083    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for quasipoisson family taken to be 10.53364)

    Null deviance: 2073.5  on 145  degrees of freedom
Residual deviance: 1393.5  on 132  degrees of freedom
AIC: NA

Number of Fisher Scoring iterations: 5

ضرایبی که با علامت * مشخص شده‌اند، از لحاظ آماری معنی‌دار بوده و حضورشان در مدل ضروری است.

۱۴. رگرسیون کاکس

از «رگرسیون کاکس» (Cox Regression) برای داده‌های وابسته به زمان استفاده می‌شود. برای درک بیشتر این موضوع به مثال‌های زیر توجه کنید:

1. زمان طی شده از وقتی که کاربر وارد حساب خود شده تا زمانی که خارج می‌شود.
2. طول دوره درمان بیماری سرطان تا مرگ بیمار.
3. زمان بین اولین و دومین حمله قلبی.

همانطور که مشاهده می‌کنید، مدل رگرسیون کاکس مانند مدل رگرسیون لجستیک است با این تفاوت که در رگرسیون لجستیک تعداد پیشامدها مهم است ولی در رگرسیون کاکس، طول یا بازه زمانی بین پیشامدها مورد بررسی قرار می‌گیرد.

چنین تحلیل‌هایی را به عنوان «تحلیل بقا» (Survival Analysis) می‌شناسیم. همانطور که مشخص است متغیر وابسته از دو بخش تشکیل شده. در بخش اول که مقداری پیوسته است، زمان یا طول دوره رخداد یک پیشامد ثبت شده و در بخش دوم،‌ رخداد یا عدم رخداد آن پیشامد مشخص شده است.

کد زیر به منظور بررسی رابطه بین طول عمر بیماران سرطانی (SurvObj) و عوامل دیگر مانند سن (age)، جنس (sex) و امتیاز کارایی کارنوفکسی ( Karnofsky performance score) که با ph.karno قابل مشاهده است، به همراه میزان کاهش وزن (wt.loss) تهیه شده است. برای دسترسی به این مجموعه داده باید کتابخانه survival را راه‌اندازی کنید.

نکته: برای دسترسی مستقیم به فایل مربوط به این داده‌ها می‌توانید اطلاعات و مقادیر متغیرها را از اینجا در قالب یک فایل فشرده دریافت کنید و بعد از خارج کردن فایل از حالت زیپ، آن را با دستور read.csv بازیابی کنید.

library(survival)
# Lung Cancer Data
# status: 2=death
lung$SurvObj <- with(lung, Surv(time, status == 2))
cox.reg <- coxph(SurvObj ~ age + sex + ph.karno + wt.loss, data = lung)
cox.reg

خروجی این کد به صورت زیر خواهد بود که نشان می‌دهد، متغیرهای سن و کاهش وزن در طول عمر فرد مبتلا به سرطان، تاثیری ندارند زیرا دارای مقدار احتمال (p value) بزرگتر از ۵ درصد هستند.

coxph(formula = SurvObj ~ age + sex + ph.karno + wt.loss, data = lung)

              coef exp(coef)  se(coef)      z       p
age       0.015140  1.015255  0.009837  1.539 0.12379
sex      -0.513955  0.598125  0.174410 -2.947 0.00321
ph.karno -0.012871  0.987211  0.006184 -2.081 0.03741
wt.loss  -0.002246  0.997757  0.006357 -0.353 0.72389

Likelihood ratio test=18.84  on 4 df, p=0.0008436
n= 214, number of events= 152 
   (14 observations deleted due to missingness)

خلاصه و جمع‌بندی

رگرسیون به یک تکنیک آماری، در «یادگیری ماشین» (Machine Learning) و داده‌‌کاوی (Data mining) گفته می‌شود که به کمک آن رابطه بین یک یا چند متغیر، مدل‌سازی می‌شود. به همین علت کسانی که در علم داده مشغول فعالیت هستند، لازم است که بر این روش آماری مسلط شوند. شیوه‌های مختلفی برای برازش خط یا منحنی روی داده‌ها وجود دارد که توسط مدل‌های مختلف رگرسیونی پیاده‌سازی شده است. نکته قابل توجه در مدل‌های رگرسیونی، کشف رابطه بین متغیرها به واسطه مقادیر آن‌ها است در حالیکه در ریاضیات براساس مدل‌ها، داده‌ها تولید می‌شوند.

در این نوشتار با جنبه‌های مختلف و انواع روش های رگرسیونی خطی و غیرخطی همچنین نحوه پیاده‌سازی آن‌ها در نرم‌افزار R آشنا شدیم و از کتابخانه‌ها و توابع مختلفی برای برازش یا حل مسائل رگرسیون با ویژگی‌های متفاوت، کمک گرفتیم. فراموش نکنید که منظور از برازش منحنی توسط مدل رگرسیونی، برآورد پارامترهای مدل محسوب می‌شود. در این بین همچنین نحوه ارزیابی و صحت مدل ارائه شده نیز مورد بحث قرار گرفت.

اگر مطلب بالا برای شما مفید بوده است، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های برنامه‌ نویسی R و نرم‌ افزار RStudio
• آموزش همبستگی و رگرسیون خطی در SPSS
• مجموعه آموزش‌های آمار و احتمالات
• رگرسیون کمترین زاویه (LAR Regression) — به زبان ساده
• رگرسیون خطی — مفهوم و محاسبات به زبان ساده
• تحلیل واریانس (Anova) — مفاهیم و کاربردها

^^