منگانومتری چیست؟ – تیتراسیون به زبان ساده

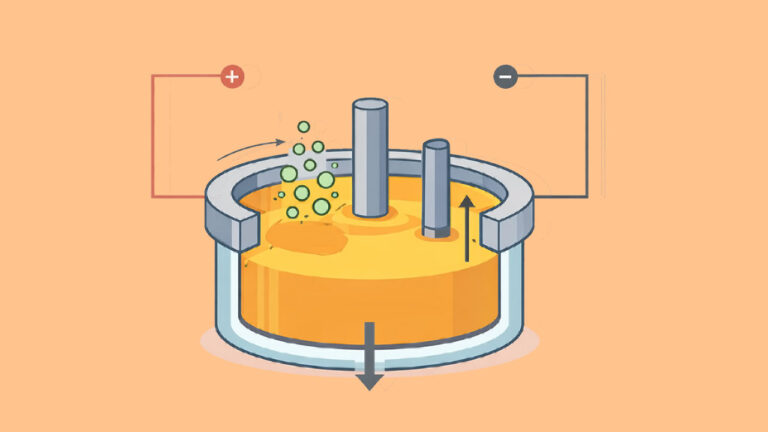
«منگانومتری» (Manganometry) روش تیتراسیونی در علم شیمی تجزیه است که به کمک آن غلظت ترکیبات مجهول را به دست می‌آورند. در این روش از پتاسیم پرمنگنات به عنوان تیترانت با غلظت مشخص، استفاده می‌شود. در این مطلب می‌خواهیم در مورد تیتراسیون کاهشی و منگانومتری به عنوان زیرشاخه‌ای از آن بدانیم و روش صحیح انجام آن را مورد بررسی قرار دهیم. همچنین به بررسی محاسباتی می‌پردازیم که برای رسیدن به غلظت مجهول در این روش، مورد نیاز هستند.

منگانومتری چیست؟

تیتراسیون منگانومتری یکی از انواع تیتراسیون است که در آن از پتاسیم پرمنگنات با فرمول شیمیایی $$KMnO_4$$ به عنوان پایه و اساس انجام تیتراسیون استفاده می‌شود و به همین دلیل به آن «منگانومتری» (Manganometry) گفته می‌شود.

تمرکز این تیتراسیون روی واکنش اکسایش و کاهشی است که توسط پتاسیم پرمنگنات قابل اندازه‌گیری خواهد بود.

پتاسیم پرمنگنات عاملی کاهنده

استفاده از پتاسیم پرمنگنات به عنوان عاملی برای اکسیداسیون نخستین بار توسط پزشکی کانادایی به نام «فلورانس مارگریت هیل» (Florence Marguriete Hill) برای تیتراسیون آهن(II) پیشنهاد شد. این تعادل کاهشی را می‌توان در محلول‌های اسیدی به‌صورت زیر نمایش داد.

$$ \mathrm{MnO}_4^{-}+8 \mathrm{H}^{+}+5 e \rightleftharpoons \mathrm{Mn}^{2+}+4 \mathrm{H}_2 \mathrm{O} $$

مقدار پتانسیل استاندارد این ماده در محلول اسیدی برابر با ۱٫۵۱ ولت است و از همین رو در محلول‌های اسیدی به عنوان عامل اکسنده قوی در نظر گرفته می‌شود. این اسید اگر به‌صورت سولفوریک اسید باشد، بسیار مطلوب است زیر با پتاسیم پرمنگنات وارد واکنش نمی‌شود. در صورتی که استفاده از اسیدی مانند هیدروکلریک اسید، واکنش زیر را ایجاد می‌کند.

 

$$2 \mathrm{MnO}_4^{-}+10 \mathrm{Cl}^{-}+16 \mathrm{H}^{+}=2 \mathrm{Mn}^{2+}+5 \mathrm{Cl}_2+8 \mathrm{H}_2 \mathrm{O}$$

توجه داشته باشید که مقداری از پرمنگنات در فرایند تولید کلر مصرف خواهد شد. این واکنش به ویژه در حضور نمک‌های آهن محتمل است و باید برای جلوگیری از آن اقداماتی را به عمل آورد. این جلوگیری شامل مواردی مانند رقیق کردن زیاد محلول، تنظیم دمای پایین و انجام تیتراسیون به‌آهستگی می‌شود. همچنین باید در انجام تیتراسیون محتویات را به طور مداوم هم زد. با این حال برخی تیتراسیون‌ها با ترکیباتی مانند آرسنیک (III) اکسید، آنتیموان (III) و هیدروژن پرکسید را در حضور هیدروکلریک اسید نیز می‌توان به انجام رساند.

 

در آنالیزهای مربوط به سنگ معدن‌های آهن، وجود هیدروکلریک اسید غلیظ تاثیرگذار خواهد بود. به‌صورتی که آهن (III) کاهش می‌یابد و آهن (II) در محلول اندازه‌گیری می‌شود. برای انجام این کار بهتر است که ۲۵ میلی‌لیتر از «محلول زیمرمان راینهات» (Zimmermann and Reinhardt's Solution)، به واکنش اضافه شود. این محلول که با نام «محلول بازدارنده» (Preventive Solution) نیز شناخته می‌شود از انحلال ۵۰ گرم منگنز (II) سولفات با فرمول شیمیایی $$MnSO_4.4H_2O$$ به ۲۵۰ میلی‌لیتر آب تهیه می‌شود.

 

سپس به آن ۱۰۰ میلی‌لیتر محلول خنک شامل سولفوریک اسید غلیظ و ۳۰۰ میلی‌لیتر آب اضافه می‌شود. در نهایت نیز ۱۰۰ میلی‌لیتر اورتوفسفریک اسید افزوده خواهد شد. حضور منگنز (II) سولفات باعث کاهش پتانسیل اکسیداسیون زوج $$MnO_4^-$$ و $$Mn(II)$$ می‌شود و آن را تبدیل به عاملی با قدرت اکسندگی کمتر می‌کند و به این صورت تمایل پرمنگنات برای اکسیداسیون یون کلر نیز کاهش می‌یابد. مشخص شده است که کارکرد بعدی منگنز (II) سولفات، محیا کردن غلظت کافی از یون $$Mn^{2+}$$ است تا با مقدار باقی‌مانده از یون پرمنگنات وارد واکنش شود. در کاهش یون پرمنگنات به منگنز (II)، احتمالا مقداری منگنز (III) نیز به وجود خواهد آمد. منگنز (II) و اورتوفسفریک اسید روی پتانسیل زوج منگنز(II)-منگنز(III) تاثیر بازدارندگی خواهند داشت، در این صورت منگنز(III) بیش از اینکه توسط یون کلرید کاهش یابد، توسط یون $$Fe^{2+}$$ کاهش پیدا می‌کند.

 

فسفریک اسید (V) با یون زرد رنگ $$Fe^{3+}$$ ترکیب شده و یون کمپلکس $$[Fe(HPO_4)]^+$$ را به وجود می‌آورد که نقطه پایانی در این صورت قابل مشاهده‌تر خواهد شد. فسفریک اسید (V) باعث کاهش پتانسیل کاهندگی سیستم آهن(III)-آهن(II) و افزایش قدرت کاهندگی یون $$Fe^{3+}$$ می‌شود. تحت این شرایط یون پرمنگنات آهن(II) را به سرعت کاهش می‌دهد و با یون کلر به آرامی وارد واکنش می‌شود.

اجزای تیتراسیون

تیتراسیون‌ها به روش‌ها و با ترکیبات متنوعی صورت می‌گیرند اما در هر روش تیتراسیون اجزایی وجود دارند که شناخت آن‌ها ضروری است. این اجزا می‌توانند در تیتراسیون‌های مختلف متفاوت باشند اما می‌توان تعریفی کلی از آن‌ها ارائه داد. در این بخش با آن‌ها آشنا خواهیم شد.

تیترانت چیست ؟

«تیترانت» (Titrant) محلولی با غلظت مشخص است که به محلول با غلظت نامشخص افزوده می‌شود و با به دست آوردن حجم مورد نیاز برای رسیدن به نقطه هم‌ارزی می‌توان به غلظت مجهول پی‌ برد. تیترانت را به کمک یک بورت به ارلن حاوی نمونه مجهول اضافه می‌کنند. در این صورت می‌توان آن را به‌آهستگی و قطره‌قطره افزود تا دقت روش تیتراسیون بالا رود.

آنالیت یا تیتران چیست ؟

«تیتراند» (Titrand) که از آن با نام آنالیت نیز یاد می‌شود، محلولی است که در این روش مورد مطالعه قرار می‌گیرد. غلظت تیتراند نامعلوم است و با انجام تیتراسیون به کمک نمونه‌ای با غلظت مشخص، آن را می‌یابیم. تیتراند معمولا اسید یا باز است اما می‌توان ترکیباتی مانند نمک را نیز در این روش مورد بررسی قرار داد. همچنین می‌توان این نقطه را از روی منحنی تیتراسیون و توسط محاسبات به دست آورد. در صورتی که استوکیومتری گونه کاهنده و اکسنده در واکنش با یکدیگر به‌صورت ۱:۱ باشد، «نقطه هم‌ارزی متقارنی» (Symmetric Equivalence Point) خواهیم داشت. در غیر این‌ صورت نقطه هم‌ارزی نزدیک‌تر به بالا یا پایین منحنی خواهد بود که به نام «نقطه هم‌ارزی نامتقارن» (Asymmetric Equivalence Point) از آن یاد می‌کنیم.

شناساگر تیتراسیون چیست ؟

شناساگر‌های تیتراسیون ترکیباتی هستند که در حالت‌های مختلف خود رنگ‌های متفاوتی را نشان می‌دهند. برای مثال شناساگری در تیتراسیون اسید و باز مناسب است که در محیطی اسیدی و بازی دارای دو رنگ متفاوت باشد. شناساگر‌های تیتراسیون کاهشی نیز در فرم اکسایشی و کاهشی خود دو رنگ متفاوت دارند. از این تغییر رنگ می‌توان به نقطه پایان تیتراسیون پی‌ برد.

نقطه هم‌ارزی چیست ؟

«نقطه هم‌ارزی» (Equivalance) تیتراسیون کاهشی زمانی اتفاق میفتد که مقدار استوکیومتری آنالیت و تیترانت با یکدیگر برابر باشد و مانند تیتراسیون اسید و باز به‌صورت تجربی به دست می‌آید. برای یافتن این نقطه می‌توان از شناساگری استفاده کرد که پایان تیتراسیون را با تغییر رنگ نشان می‌دهد. در برخی از تیتراسیون‌های کاهشی اجزای واکنش به‌صورت خودبه‌خودی تغییر رنگ می‌دهند و نیازی به استفاده از شناساگر نیست.

تیراسیون کاهشی چیست؟

«تیتراسیون کاهشی» (Redox Titration) نوعی از تیتراسیون است که بر اساس واکنش کاهشی بین یک آنالیت و تیترانت انجام می‌شود. در این واکنش بر حسب نیاز از شناساگر کاهشی یا پتانسیومتر استفاده می‌شود.

 

برای مثال می‌توان به واکنش بین ید با عاملی اشاره کرد که طی آن یدید تولید می‌شود. در این تیتراسیون برای تشخیص نقطه پایان هم‌ارزی از شناساگر نشاسته بهره می‌گیرند. برای تبدیل $$I_2$$ به $$I^-$$ می‌توان از تیوسولفید با فرمول شیمیایی $$S_2O_3^{2-}$$ استفاده کرد. در این واکنش بعد از اینکه تمامی یدها به یون یدید تبدیل شوند، محلول آبی رنگ تبدیل به محلولی بی‌رنگ می‌شود که اصطلاحا به آن «تیتراسیون یدومتری» (Iodometric Titration) گفته می‌شود. در جدول زیر تعدادی از مهم‌ترین انواع تیتراسیون کاهشی را مشاهده می‌کنید. توجه داشته باشید که این دسته‌بندی بر اساس نوع تیترانت آن‌ها انجام شده است.

بنابراین متوجه می‌شویم که منگانومتری یکی از انواع تیتراسیون کاهشی است و تمامی مفاهیم مربوط به تیتراسیون کاهشی برای آن قابل تعمیم است. برای درک بهتر مفهوم منگانومتری نیاز است تا با یک سری اصطلاحات آشنا شویم. در بخش بعد تعداد از آن‌ها را آورده‌ایم.

شناساگر تیتراسیون کاهشی

به طور کلی از سه نوع شناساگر برای تشخیص نقطه هم‌ارزی تیتراسیون کاهشی استفاده می‌شود. گونه‌های اکسیدی و کاهشی تیترانت‌هایی مانند $$MnO_4^-$$ از خود رنگ‌های متفاوتی را نشان می‌دهند. در این مورد $$MnO_4$$ در محلول دارای رنگ بنفش تندی است با این‌حال وقتی به عنوان تیترانت مورد استفاده قرار می‌گیرد، تا زمان رسیدن به نقطه هم‌ارزی بی‌رنگ خواهد بود. نقطه هم‌ارزی در لحظه‌ای به دست می‌آيد که با قطره‌ای از $$MnO_4^-$$ کوچک‌ترین رنگ مشاهده شود، در واقع زمانی است که محلول بی‌رنگ شروع به نشان دادن رنگی بنفش از خود می‌کند.

توجه داشته باشید که در صورتی که از محلول‌های بسیار رقیق پتاسیم پرمنگنات برای تیتراسیون استفاده شود، بهتر است برای تشخیص راحت‌تر و دقیق‌تر نقطه هم‌ارزی از شناساگر تیتراسیون استفاده شود. تعدادی از شناساگرهایی که می‌توان در این مورد به کار گرفت، در لیست زیر آورده‌ شده‌اند.

• سدیم دی‌فنیل آمین سولفونات
• فرورین
• ان فنیل آنترانیلیک اسید

برای درک بهتر رابطه بین پتانسیل و رنگ شناساگر، نیم‌واکنش کاهشی شناساگر را در نظر بگیرید. این نیم‌واکنش را می‌توان به‌صورت زیر نوشت. توجه داشته باشید که برای سهولت، هر دو فرم خنثی نوشته شده‌اند اما در واقع به دلیل تغییر عدد اکسایش، ممکن نیست که هر دو خنثی باشند.

 

$$\mathrm{In_{ox}}+ne^-rightleftharpoons \mathrm{In_{red}}$$

• $$In_{OX}$$: فرم اکسایش یافته شناساگر
• $$In_{red}$$: فرم کاهش‌یافته شناساگر

رابطه نرنست را برای تعیین پتانسیل این نیم‌واکنش به‌صورت زیر می‌نویسیم.

$$E=E^o_mathrm{In_{\large ox}/In_{\large red}}-dfrac{0.05916}{n}logmathrm{\dfrac{[In_{red}]}{[In_{ox}]}}$$

با تبدیل فرم اکسایشی به فرم کاهشی، تغییر رنگی در شناساگر مشاهده می‌شود. در این صورت همان‌طور که در نمودار زیر پیداست، نقطه پایانی تیتراسیون در انتهای این بازه خواهد بود.

$$E=E^o_mathrm{In_{\large ox}/In_{\large red}}pmdfrac{0.05916}{n}$$

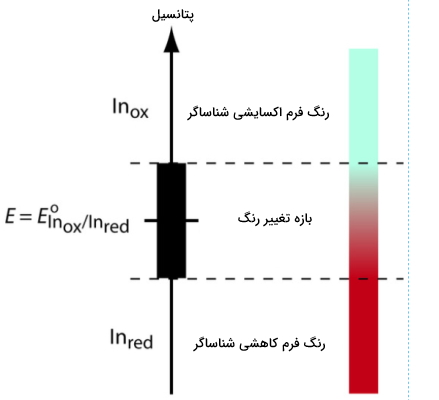
در جدول زیر تعدادی از شناساگرهای تیتراسیون اکسایشی کاهشی را به همراه بازه تغییر رنگشان مشاهده می‌کنید.

مثال تیتراسیون کاهشی

برای مثال می‌خواهیم تیتراسیون پتاسیم پرمنگنات را در برابر اگزالیک اسید مورد بررسی قرار دهیم. در مرحله اول محلول استانداری از اگزالیک اسید به حجم ۲۵۰ میلی‌لیتر آماده می‌کنیم. همان‌طور که می‌دانید با جمع بستن جرم اتمی عناصر موجود در آن می‌توان، جرم مولکولی اگزالیک اسید را به دست آورد. این کار را به‌صورت زیر انجام می‌دهیم.

$$  H_2C_2O_4.2H_2O = 126$$

با توجه به اینکه وزن اگزالیک اسید مورد نیاز برای تهیه ۱۰۰۰ میلی‌لیتر محلول ۱ مولار آن برابر با ۱۲۶ گرم است، وزن مورد نیاز برای تهیه ۲۵۰ میلی‌لیتر محلول ۰٫۱ مولار آن را می‌توان به روش زیر به دست آورد.

$$\frac{126}{1000} times250 \times 0.1 = 3.15\;g $$

منحنی تیتراسیون کاهشی

برای بررسی تیتراسیون‌های کاهشی از منحنی تیتراسیون بهره می‌گیرند. توجه داشته باشید که در تیتراسیون‌های کاهشی تغییرات پتانسیل واکنش مورد بررسی قرار می‌گیرد و مانند تیتراسیون اسید و باز، مبنا بر تغییرات غلظت و حجم گونه‌ها نیست. در ادامه به بررسی چگونگی تفسیر این نمودارها خواهیم پرداخت.

طبق «رابطه نرست» (Nerst Equation) در یک واکنش اکسایشی- کاهشی، پتانسیل محلول را می‌توان به غلظت واکنش‌دهنده و محصول مرتبط دانست. برای مثال تیتراسیونی را در نظر بگیرید که در آن آنالیت در حالت کاهش‌یافته خود با تیترانتی به حالت اکسایش‌یافته خود وارد واکنش می‌شود. این را می‌توان به‌صورت ساده مانند زیر نمایش داد.

$$ A_textrm{red}+B_textrm{ox} \rightleftharpoons B_textrm{red}+A_textrm{ox} $$

در این تعادل $$A_{ox}$$ نشان‌دهنده آنالیت در حالت اکسایش‌یافته خود و $$B_{red}$$ نشان‌دهنده تیترانت در حالت کاهش‌یافته است. پتانسیل این واکنش، در واقع تفاوت بین پتانسیل کاهشی برای هر «نیم‌واکنش» (Half Reaction) است که آن را به‌صورت زیر نشان می‌دهیم.

$$ E_textrm{rxn}=E_{B_mathrm{\Large ox}/B_mathrm{\Large red}}-E_{A_mathrm{\Large ox}/A_mathrm{\Large red}} $$

با افزودن تیترانت، واکنش بین آنالیت و تیترانت به نقطه‌ای می‌رسد که در آن تعادل برقرار خواهد بود. از آن‌جایی که مقدار پتانسیل در نقطه تعادل برابر ۰ است، طبق رابطه بالا، پتانسیل کاهشی آنالیت و تیترانت مانند زیر با یکدیگر برابر می‌شود. این نکته از اهمیت بسیار زیادی برخوردار است زیرا با دانستن آن، می‌توانیم برای بررسی روند کار، هر کدام از آنالیت یا تیترانت را در نظر بگیریم.

$$ E_{B_mathrm{\Large ox}/B_mathrm{\Large red}}=E_{A_mathrm{\Large ox}/A_mathrm{\Large red}} $$

قبل از رسیدن به نقطه هم‌ارزی، محتویات تیتراسیون شامل مقادیر قابل‌توجهی از گونه اکسیدی و کاهشی آنالیت است و در عین حال غلظت تیترانت واکنش‌نداده نیز بسیار پایین است. بنابراین در این نقطه محاسبه مقدار پتانسیل نیم‌واکنش آنالیت از رابطه نرنست آسان‌تر خواهد بود. این رابطه در زیر آورده شده است.

$$E_textrm{rxn}= E^o_{A_mathrm{\Large ox}/A_mathrm{\Large red}}-dfrac{RT}{nF}lndfrac{[A_textrm{red}]}{[A_textrm{ox}]} $$

همچین بنابر دلایل ذکر شده، محاسبه پتانسیل نیم‌واکنش تیترانت طبق رابطه نرنست، بعد از رسیدن به نقطه هم‌ارزی راحت‌تر خواهد بود. این محاسبه به‌صورت زیر قابل انجام است.

$$ E_textrm{rxn}= E^o_{B_mathrm{\Large ox}/B_mathrm{\Large red}}-dfrac{RT}{nF}lndfrac{[B_textrm{red}]}{[B_textrm{ox}]} $$

با وجود اینکه رابطه نرنست بر اساس «پتانسیل حالت استاندارد» (Standard State Potential) نیم‌واکنش‌های طراحی شده است، در بسیاری از موراد به جای آن‌ها از «پتانسیل فرمال»‌ (Formal Potential) وابسته به ماتریس محیط، استفاده می‌شود. این مقادیر را می‌توان با مراجعه به کتاب‌های مرجع یافت و مورد استفاده قرار داد.

محاسبه منحنی تیتراسیون کاهشی

همان‌طور که می‌دانید هدف از انجام تیتراسیون به دست آوردن غلظت مجهول یک محلول، آنالیت، توسط تیترانت با غلظت معلوم است. در این بخش می‌خواهیم بدانیم چطور به کمک تیتراسیون‌های کاهشی که مبنای منحنی آن‌ها بر پتانسیل کاهشی است، می‌توان این محاسبات را انجام داد. در ادامه با بررسی تعدادی مثال این موضوع را روشن خواهیم کرد.

می‌خواهیم منحنی تیتراسیون را برای تیتراسیون ۵۰ میلی‌لیتر از $$Fe^{2+}$$ با مولاریته ۰٫۱ را با $$Ce^{4+}$$ با مولاریته ۰٫۱ در ماتریس پرکلریک اسید ۱ مولار با فرمول شیمیایی $$HClO_4$$ محاسبه کنیم. واکنش این تیتراسیون به‌صورت زیر است.

$$\textrm{Fe}^{2+}(aq)+textrm{Ce}^{4+}(aq)\rightleftharpoons \textrm{Ce}^{3+}(aq)+textrm{Fe}^{3+}(aq)\tag{9.15} $$

در پرکلریک اسید ۱ مولار، پتانسیل فرمال برای کاهش $$Fe^{3+}$$ به $$Fe^{2+}$$ برابر با ۰٫۷۶۷ ولت و برای کاهش $$Ce^{4+}$$ به $$Ce{3+}$$ برابر با ۱٫۷ ولت است. از آنجا که ثابت تعادل این واکنش بسیار بزرگ است، ممکن است تصور کنیم که واکنش بین آنالیت و تیترانت به‌طور کامل انجام می‌شود. با طی مراحل زیر به منحنی تیتراسیون خواهیم رسید.

 

مرحله اول:‌ محاسبه حجم تیترانت مورد نیاز برای رسیدن به نقطه هم‌ارزی

در ابتدا باید حجم $$Ce^{4+}$$ مورد نیاز برای رسیدن تیراسیون به نقطه هم‌ارزی را محاسبه کنیم. از استوکیومتری واکنش بالا، می‌توانیم رابطه بین مول‌ها را به‌صورت زیر بنویسیم.

$$ \textrm{moles Fe}^{2+}=\textrm{moles Ce}^{4+} $$

$$ M_textrm{Fe}\times V_textrm{Fe} = M_textrm{Ce}\times V_textrm{Ce} $$

در نتیجه حجمی که در آن نقطه هم‌ارزی اتفاق می‌افتد برابر است با:

$$V_textrm{eq} = V_textrm{Ce} = \dfrac{M_textrm{Fe}V_textrm{Fe}}{M_textrm{Ce}}=\dfrac{\textrm{(0.100 M)(50.0 mL)}}{\textrm{(0.100 M)}}=\textrm{50.0 mL} $$

مرحله دوم: محاسبه پتانسیل قبل از هم‌ارزی به کمک غلظت گونه‌های اکسیدی و کاهشی آنالیت و رابطه نرنست برای نیم‌واکنش کاهشی آن

همان‌طور که پیشتر اشاره کردیم، غلظت $$Fe^{2+}$$ واکنش‌نداده و غلظت $$Fe^{3+}$$ را می‌توان به سادگی به دست آورد. در همین راستا ابتدا پتانسیل را به کمک رابطه نرنست برای این نیم‌واکنش محاسبه می‌کنیم.

$$ E = E^o_mathrm{\large Fe^{3+}/Fe^{2+}} - \dfrac{RT}{nF}logdfrac{[\mathrm{Fe^{2+}}]}{[\mathrm{Fe^{3+}}]}=+0.767textrm V - 0.05916logdfrac{[\mathrm{Fe^{2+}}]}{[\mathrm{Fe^{3+}}]}\tag{9.16} $$

برای مثال غلظت $$Fe^{2+}$$ و $$Fe^{3+}$$ بعد از افزودن ۱۰ میلی‌لیتر تیترانت به‌صورت زیر به دست می‌آيد.

$$ \begin{align}
[\textrm{Fe}^{2+}]&\;=\dfrac{\textrm{initial moles Fe}^{2+} - \textrm{moles Ce}^{4+}\textrm{ added}}{\textrm{total volume}}=\dfrac{M_textrm{Fe}V_textrm{Fe} - M_textrm{Ce}V_textrm{Ce}}{V_textrm{Fe}+V_textrm{Ce}}
&\;mathrm{= \dfrac{(0.100\;M)(50.0\;mL)-(0.100\;M)(10.0\;mL)}{50.0\;mL+10.0\;mL} = 6.67times10^{-2}\;M}
\end{align} $$

$$ \begin{align}
[\mathrm{Fe^{3+}}]&\;=\mathrm{\dfrac{moles\;Ce^{4+}\;added}{total\;volume}}=\dfrac{M_textrm{Ce}V_textrm{Ce}}{V_textrm{Fe} + V_textrm{Ce}}
&\;=\dfrac{\textrm{(0.100 M)(10.0 mL)}}{\textrm{50.0 mL + 10.0 mL}}=1.67times10^{-2}\textrm{ M}
\end{align} $$

با جای‌گذاری این غلظت‌ها در رابطه بالا پتانسیل به دست می‌آید.

$$E = +0.767textrm{ V} - 0.05916 logdfrac{6.67times10^{-2}\textrm{ M}}{1.67times10^{-2}\textrm{ M}}=+0.731textrm{ V} $$

مرحله سوم: محاسبه پتانسیل پس از نقطه هم‌ارزی به کمک غلظت گونه‌های اکسیدی و کاهشی تیترانت و رابطه نرنست برای نیم‌واکنش کاهشی آن

پس از نقطه هم‌ارزی، غلظت $$Ce^{3+}$$ و غلظت $$Ce^{4+}$$ مازاد را می‌توان به سادگی محاسبه کرد. در همین راستا پتانسیل نیم‌واکنش آن را به کمک رابطه نرنست به دست می‌آوریم.

$$ E=E^o_mathrm{\large{Ce^{4+}/Ce^{3+}}}-dfrac{RT}{nF}logmathrm{\dfrac{[Ce^{3+}]}{[Ce^{4+}]}}=+ 1.70textrm{ V} - 0.05916 logmathrm{\dfrac{[Ce^{3+}]}{[Ce^{4+}]}}\tag{9.17} $$

به‌طور مثال پس از افزودن ۶۰ میلی‌لیتر تیترانت، غلظت‌ها به شکل زیر قابل محاسبه هستند.

$$ \begin{align}
[\textrm{Ce}^{3+}]&\;={\dfrac{\textrm{initial moles Fe}^{2+}}{\textrm{total volume}}}=\dfrac{M_textrm{Fe}V_textrm{Fe}}{V_textrm{Fe}+V_textrm{Ce}}
&\;=\dfrac{\textrm{(0.100 M)(50.0 mL)}}{\textrm{50.0 mL + 60.0 mL}}=4.55times10^{-3}\textrm{ M}
\end{align} $$

$$ \begin{align}
[\textrm{Ce}^{4+}]&\;=\dfrac{\textrm{moles Ce}^{4+}\textrm{ added} - \textrm{initial moles Fe}^{2+}}{\textrm{total volume}}=\dfrac{M_textrm{Ce}V_textrm{Ce}-M_textrm{Fe}V_textrm{Fe}}{V_textrm{Fe}+V_textrm{Ce}}
&\;=\dfrac{\textrm{(0.100 M)(60.0 mL)}-textrm{(0.100 M)(50.0 mL)}}{\textrm{50.0 mL + 60.0 mL}}=9.09times10^{-3}\textrm{ M}
\end{align}$$

در پایان نیز با جایگذاری مقادیر به دست آمده در رابطه نرنست خواهیم داشت.

$$ E=+1.70textrm{ V}-0.05916logdfrac{4.55times10^{-2}\textrm{ M}}{9.09times10^{-3}\textrm{ M}}=+1.66textrm{ V} $$

مرحله چهارم:‌ محاسبه پتانسیل نقطه هم‌ارزی

در نقطه هم‌ارزی تیتراسیون، پتانسیل نقطه هم‌ارزی در هر دو رابطه بالا با یکدیگر یکسان است. با افزودن این دو رابطه به هم خواهیم داشت:

$$ 2E_textrm{eq}= E^o_mathrm{\large Fe^{3+}/Fe^{2+}}+E^o_mathrm{\large Ce^{4+}/Ce^{3+}}-0.05916logdfrac{\mathrm{[{Fe}^{2+}][Ce^{3+}]}}{\mathrm{[Fe^{3+}][Ce^{4+}]}} $$

از آنجا که در نقطه هم‌ارزی غلظت $$Fe^{2+}$$ با $$Ce^{4+}$$ و غلظت $$Ce^{3+}$$ با $$Fe^{3+}$$ برابر هستند، مقدار لگاریتم برابر با ۰ می‌شود و پتانسیل نقطه هم‌ارزی به‌صورت زیر به دست می‌آید.

$$ E_textrm{eq}=\dfrac{E^o_mathrm{\large Fe^{3+}/Fe^{2+}} + E^o_mathrm{\large Ce^{4+}/Ce^{3+}}}{2}=\dfrac{\textrm{0.767 V + 1.70 V}}{2}=1.23textrm{ V}$$

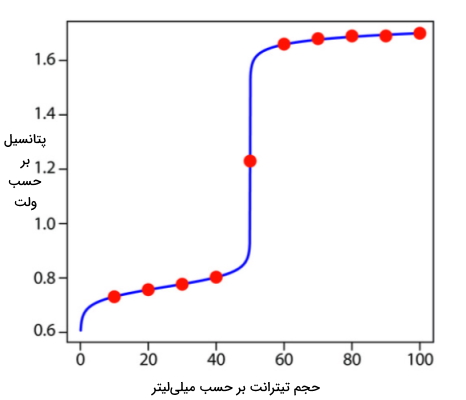
روند محاسبات برای این تیتراسیون به‌صورت تشریح شده است. در جدول زیر محاسبات بیشتری انجام شده است که می‌توان با بهره‌گیری از آن‌ها منحنی این تیتراسیون را رسم کرد. به این تیتراسیون کاهشی که از سریم به عنوان تیترانت استفاده کرده است، سریمتری گفته می‌شود.

در این منحنی نقاط قرمز مختصاتی هستند که در جدول بالا محاسبه شده‌اند، خط آبی نشان‌دهنده منحنی تیتراسیون ۵۰ میلی‌لیتر $$Fe^{2+}$$ با مولاریته ۰٫۱ به کمک $$Ce^{4+}$$ با مولاریته ۰٫۱ است.

مثال تیتراسیون منگانومتری

در تیتراسیونی تصمیم داریم $$Fe^{2+}$$ را توسط $$MnO_4^-$$ تیتر کنیم. تعادل این واکنش کاهشی-اکسایشی به‌صورت زیر قابل مشاهده است.

$$5textrm{Fe}^{2+}(aq)+textrm{MnO}_4^-(aq)+8textrm H^+(aq)\rightarrow 5textrm{Fe}^{3+}(aq)+textrm{Mn}^{2+}(aq)+mathrm{4H_2O}$$

توجه داشته باشید که در این واکنش‌ها معمولا به جای $$H_3O^+$$ از $$H^+$$ استفاده می‌شود. نیاز داریم نیم‌واکنش هر کدام از گونه‌ها را بنویسیم. در این‌صورت دو نیم‌واکنش زیر به دست می‌آیند.

$$\textrm{Fe}^{2+}(aq)rightarrowtextrm{Fe}^{3+}(aq)+e^-$$

$$\textrm{MnO}_4^-(aq)+8textrm H^+(aq)+5e^-rightarrow \textrm{Mn}^{2+}(aq)+4mathrm{H_2O}(l)$$

برای این دو رابطه نرنست را یادداشت می‌کنیم.

$$E=E^o_mathrm{\large Fe^{3+}/Fe^{2+}}-0.05916logdfrac{[\textrm{Fe}^{2+}]}{[\textrm{Fe}^{3+}]}$$

$$E=E^o_mathrm{\large MnO_4^-/Mn^{2+}}-dfrac{0.05916}{5}logdfrac{[\textrm{Mn}^{2+}]}{{[MnO_4^- ][H^+]^8}}$$

پیش از جمع بستن دو رابطه باید دومی را در عدد ۵ ضرب کنیم تا بتوان لگاریتم‌ها را با یکدیگر جمع بست. برای این کار به‌صورت زیر عمل می‌کنیم.

$$6E=E^o_mathrm{\large Fe^{3+}/Fe^{2+}}+5E^o_mathrm{\large MnO_4^-/Mn^{2+}}-0.05916logmathrm{\dfrac{[Fe^{2+}][Mn^{2+}]}{[Fe^{3+}][{MnO_4^-}][H^+]^8}}$$

می‌دانیم که در نقطه هم‌ارزی دو رابطه زیر پابرجا هستند:

$$[\textrm{Fe}^{2+}]=5times[\textrm{MnO}_4^-]$$

$$[\textrm{Fe}^{3+}]=5times[\textrm{Mn}^{2+}]$$

در مرحله بعد ابتدا این دو رابطه را در روابط پیشین جای‌گذاری می‌کنیم و سپس با بازآرایی آن‌ها خواهیم داشت:

$$6E_textrm{eq}=E^o_mathrm{\large Fe^{3+}/Fe^{2+}}+5E^o_mathrm{\large MnO_4^-/Mn^{2+}}-0.05916logmathrm{\dfrac{5[{MnO_4^-}][Mn^{2+}]}{5[Mn^{2+}][{MnO_4^-}][H^+]^8}}$$

$$E_textrm{eq}=\dfrac{E^o_mathrm{\large Fe^{3+}/Fe^{2+}} + 5E^o_mathrm{\large MnO_4^-/Mn^{2+}}}{6}-dfrac{0.05916}{6}logdfrac{1}{[\textrm H^+]^8}$$

$$E_textrm{eq}=\dfrac{E^o_mathrm{\large Fe^{3+}/Fe^{2+}}+5E^o_mathrm{\large MnO_4^-/Mn^{2+}}}{6}+dfrac{0.05916times8}{6}\log[\textrm H^+]$$

$$E_textrm{eq}=\dfrac{E^o_mathrm{\large Fe^{3+}/Fe^{2+}}+5E^o_mathrm{\large MnO_4^-/Mn^{2+}}}{6}-0.07888textrm{pH}$$

با توجه به این رابطه، در مقدار $$pH$$ برابر با ۱، در سولفوریک اسید، پتانسیل را می‌توان به‌صورت زیر محاسبه کرد.

$$E_textrm{eq}=\dfrac{0.768+5times1.51}{6}-0.07888times1=1.31textrm{ V}$$

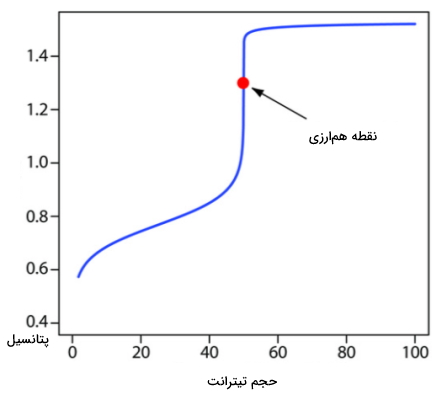
منحنی این تیتراسیون را می‌توان مانند تصویر با جای‌گذاری حجم‌های مختلف از پرمنگنات به دست آورد. توجه داشته باشید که این منحنی از نوع منحنی تیتراسیون نامتقارن است که در آن نقطه هم‌ارزی به بالای منحنی نزدیک‌تر قرار دارد.

ویژگی‌های پتاسیم پرمنگنات

برای درک بهتر این نوع تیتراسیون، شناخت ویژگی‌های پتاسیم پرمنگنات کمک به‌سزایی خواهد کرد. پتاسیم پرمنگنات که آن را با فرمول شیمیایی $$KMnO_4$$ نشان می‌دهند، اکسنده‌ای بسیار قوی است. این قدرت اکسندگی به ویژه در محلول‌های زیر نمود پیدا می‌کند.

• محلول‌هایی که باز ضعیف هستند.
• محلول‌هایی که خنثی هستند.
• محلول‌هایی که اسید ضعیف هستند.

ذکر این نکته خالی از لطف نیست که در محلولی با خاصیت بازی قوی، یون‌های پرمنگنات می‌توانند کاهش پیدا کنند. کاهش پرمنگنات در این محلول منجر به تولید یون منگنات با فرمول شیمیایی $$Mn^{2+}$$ می‌شود. طی این تغییر رنگ محلول نیز تغییر پیدا می‌کند. هنگامی که پتاسیم پرمنگنات به یون پرمنگنات کاهش می‌یابد، محلول رنگی سبز خواهد داشت. بنابراین برای کنترل غلظت یک اسید قوی، استفاده از آن توصیه می‌شود. زیرا هیچ واکنش جانبی در این صورت اتفاق نمی‌افتد و وقوع واکنش و تغییر رنگ آنی خواهد بود. پتاسیم پرمنگنات به دلیل خاصیت ضدعفونی‌کنندگی که دارد در علم پزشکی و دامپزشکی نیز شناخته‌شده و پرکاربرد است. از این ماده برای تمیز کردن زخم‌ها استفاده می‌شود.

 

منگانومتری در محلول قلیایی

پتاسیم پرمنگنات می‌تواند در محلول قلیایی قوی نیز مورد استفاده قرار گیرد. در این مورد به دو واکنش پشت هم زیر دقت کنید.

واکنش اول با سرعت بالایی صورت می‌گیرد.

$$ \mathrm{MnO}_4^{-}+e \rightleftharpoons \mathrm{MnO}_4^{2-} $$

واکنش دوم به‌صورت زیر و آهسته انجام می‌شود.

$$
\mathrm{MnO}_4^{2-}+2 \mathrm{H}_2 \mathrm{O}+2 e \rightleftharpoons \mathrm{MnO}_2+4 \mathrm{OH}^{-}
$$

پتانسیل استاندارد واکنش اول ۰٫۵۶ ولت و پتانسیل استاندارد واکنش دوم ۰٫۶ ولت است. با کنترل شرایط آزمایش (افزودن یون‌های باریوم)، می‌توانیم تنها واکنش اول را داشته باشیم. در محلول قلیایی با شدت متوسط، پرمنگنات کاهش پیدا می‌کند و منگنز دی‌اکسید را به وجود می‌آورد. واکنش این نیم سلول را می‌توان به‌‌صورت زیر نشان داد.

$$ \mathrm{MnO}_4^{-}+2 \mathrm{H}_2 \mathrm{O}+3 e \rightleftharpoons \mathrm{MnO}_2+4 \mathrm{OH}^{-} $$

پتاسیم پرمنگنات استانداری اولیه نیست زیرا در دست داشتن آن به‌صورت کاملا خالص و عاری از منگنز دی‌اکسید دشوار است. به علاوه، آب مقطر دارای موادی کاهنده است که می‌تواند با پتاسیم پرمنگنات وارد واکنش شود و منگنز دی‌اکسید را به وجود بیاورد. حضور منگنز دی‌اکسید بسیار نامطلوب است زیرا واکنش تخریب محلول پرمنگنات را کاتالیز می‌کند. به واکنش زیر دقت کنید.

$$ 4 \mathrm{MnO}_4^{-}+2 \mathrm{H}_2 \mathrm{O}rightleftharpoons4 \mathrm{MnO}_2+3 \mathrm{O}_2+4 \mathrm{OH}^{-} $$

پرمنگنات به ذات در حضور یون‌های منگنز (II) ناپایدار است. به واکنش زیر توجه کنید.

$$ 2 \mathrm{MnO}_4^{-}+3 \mathrm{Mn}^{2+}+2 \mathrm{H}_2 \mathrm{O}rightleftharpoons5 \mathrm{MnO}_2+4 \mathrm{H}^{+} $$

این واکنش در محلول اسیدی کند است اما در محلول خنثی با سرعت بسیار زیادی انجام می‌شود. به همین دلیل محلول پتاسیم پرمنگنات به ندرت از حل کردن مقدار مورد نیاز آن به‌صورت جامد در آب تهیه می‌شود. به جای آن به محلول تازه تهیه شده آن گرما داده و آن را می‌جوشانند و به مدت چند ساعت در حمام بخار قرار می‌دهند. سپس این محلول را به کمک فیلتری که دارای محیطی فاقد هر گونه کاهنده باشد، صاف می‌کنند. از این مورد می‌توان به قیف‌های دارای سینتر گلس اشاره کرد. در برخی موارد محلول را پیش از صاف کردن، به مدت ۲ تا ۳ روز در دمای اتاق رها می‌کنند.

 

توجه داشته باشید که تمیز بودن ظروف از اهمیت بالایی برخوردار است. نیاز است که ظروف از هرگونه روغن یا منگنز دی‌اکسید به‌جامانده از پیش پاک‌سازی شوند. این کار را می‌توان با شستشو با مخلوط تمیزکننده دی‌کرومات-سولفوریک اسید و سپس با آب مقطر به انجام رساند. همان‌طور که می‌دانید محلول‌های اسیدی و بازی از محلول‌های خنثی ناپایدارتر هستند. محلول پرمنگنات را باید دور از هرگونه نور و در ظرفی تیره نگهداری کرد.

نکات تکمیلی منگانومتری

تا اینجا دانستیم که منگانومتری روشی از تیتراسیون کاهشی است که به کمک پتاسیم پرمنگنات انجام می‌شود. در این بخش به مرور تعدادی از مهم‌ترین نکته‌هایی می‌پردازیم که نیاز است بدانیم.

• از آنجا که در این تیتراسیون نیاز به محیط اسیدی داریم، پتاسیم پرمنگنات به ارلنی اضافه می‌شود که شامل سولفوریک اسید رقیق است.
• وجود اسید غلیظ در نمونه به‌صورت سولفوریک اسید یا نیتریک اسید در واکنش ایجاد تداخل می‌کند.
• پتاسیم پرمنگنات محلول استاندارد اولیه نیست و شامل مقادیری از منگنز دی‌اکسید است.
• برای استاندارد کردن پتاسیم پرمنگنات از اگزالیک اسید یا نمک موهر استفاده می‌شود.
• در این تیتراسیون وجود شناساگر ضروری نیست و می‌توان از رنگ پتاسیم پرمنگنات نقطه پایان را تشخیص داد.

ابزار مور نیاز برای انجام تیتراسیون منگانومتری

در این روش تیتراسیون نیز مانند باقی روش‌های نیاز به ابزارهای خاصی داریم تا بتوان واکنش را دقیق‌تر انجام و خطاها را کاهش داد. از مهم‌ترین ابزارهای آزمایشگاهی که برای این روش نیاز است می‌توان به موارد زیر اشاره کرد.

• پیپت حجمی
• ارلن
• بورت

تاریخچه تیتراسیون منگانومتری

استفاده از این روش تیتراسیون به سال‌های بسیار دوری برمی‌گردد. در واقع بیش از یک دهه است که شیمی‌دان‌‌ها، تیتراسیون پرمنگانومتری را در شرایط متفاوتی انجام می‌دهند. روش‌های تیتراسیونی در سال ۱۸۴۵ توسط یک شیمی‌دان فرانسوی به نام اتین هانری (Etienne Ossian Henry) ابداع و به کار گرفته شد.

مثال و حل تمرین از منگانومتری

تا اینجا به مفهوم تیتراسیوت منگانومتری و نحوه انجام آن آشنا شدیم. در این بخش با بررسی تعدادی مثال و تمرین درک خود را از این موضوع عمیق‌تر خواهیم کرد.

حل مثال از منگانومتری

در این بخش ابتدا تعدادی مثال را به همراه پاسخ تشریحی مورد بررسی قرار می‌دهیم. با حل این مثال‌ها توانایی حل تمرین‌های مشابه را پیدا می‌کنیم.

مثال اول

واکنش تیتراسیونی را بنویسید که در آن اگزالیک اسید توسط پتاسیم پرمنگنات تیتر شود.

پاسخ

این واکنش را می‌توان به‌صورت زیر نمایش داد.

$$ 2KMnO_4+3H_2SO_4+5H_2C_2O_4 \rightarrow K_2SO_4+2MnSO_4+8H_2O+10CO_2 $$

مثال دوم

منحنی تیتراسیون را برای تیتراسیون بین ۵۰ میلی‌لیتر $$Sn^{2+}$$ با مولاریته ۰٫۰۵ به همراه $$Ti^{3+}$$ با مولاریته ۰٫۱ به دست آورید. در این تیتراسیوت هم تیترانت و هم آنالیت در $$HCl$$ هستند. همچنین می‌توان واکنش بین آن‌ها را به صورت زیر نمایش داد.

$$ \textrm{Sn}^{2+}(aq)+textrm{Tl}^{3+}(aq)\rightarrow \textrm{Sn}^{4+}(aq)+textrm{Tl}^+(aq)$$

پاسخ

ابتدا حجم مورد نیاز از $$Ti^{3+}$$ مورد نیاز برای رسیدن به نقطه هم‌ارزی را محاسبه می‌کنیم.

$$V_textrm{eq}=V_textrm{Tl}=\dfrac{M_textrm{Sn}V_textrm{Sn}}{M_textrm{Tl}}=\mathrm{\dfrac{(0.050\;M)(50.0\;mL)}{0.100\;M}=25.0\;mL}$$

محاسبه غلظت $$Sn^{2+}$$ واکنش‌نداده و غلظت $$Sn^{4+}$$ پیش از رسیدن به نقطه هم‌ارزی آسان است. به همین دلیل پتانسیل نیم‌واکنش‌ آن‌ها را به کمک رابطه نرنست به دست می‌آوریم. برای مثال با افزودن ۱۰ میلی‌لیتر از تیترانت خواهیم داشت:

$$\mathrm{[Sn^{2+}]=\dfrac{(0.050\;M)(50.0\;mL)-(0.100\;M)(10.0\;mL)}{50.0\;mL+10.0\;mL}=0.0250\;M}$$

$$\mathrm{[Sn^{4+}]=\dfrac{(0.100\;M)(10.0\;mL)}{50.0\;mL+10.0\;mL}=0.0167\;M}$$

با جایگذاری در رابطه نرنست می‌توانیم این‌طور بنویسیم:

$$E=\mathrm{+0.139\;V-dfrac{0.05916}{2}logdfrac{0.0250\;M}{0.0167\;M}=+0.134\;V}$$

همچنین پس از رسیدن به نقطه هم‌ارزی محاسبه غلظت $$Ti^+$$ و $$Ti^{3+}$$ مازاد ساده است و به همین دلیل پتانسیل آن را به کمک رابطه نرنست این نیم‌واکنش به دست می‌آوریم. مثلا اگر ۴۰ میلی‌لیتر از تیترانت اضافه شده باشد، برای محاسبه مقادیر غلظت به روش زیر خواهیم داشت:

$$\mathrm{[Tl^+]=\dfrac{(0.0500\;M)(50.0\;mL)}{50.0\;mL+40.0\;mL}=0.0278\;M}$$

$$\mathrm{[Tl^{3+}]=\dfrac{(0.100\;M)(40.0\;mL)-(0.0500\;M)(50.0\;mL)}{50.0\;mL+40.0\;mL}=0.0167\;M}$$

سپس به‌صورت زیر، مقادیر به دست آمده را در رابطه نرنست این نیم‌واکنش جایگذاری می‌کنیم.

$$E=\mathrm{+0.77\;V-dfrac{0.05916}{2}logdfrac{0.0278\;M}{0.0167\;M}=+0.76\;V}$$

همچنین در نقطه هم‌ارزی تیتراسیون، پتانسیل نقطه هم‌ارزی را محاسبه می‌کنیم.

$$E_textrm{eq}=\mathrm{\dfrac{0.139\;V+0.77\;V}{2}=0.45\;V}$$

با استفاده از همین روش می‌توان مقادیر پتانسیل را در حجم‌های مختلف تیترانت محاسبه کرد و از آن‌ها برای رسم منحنی تیتراسیون بهره گرفت. تعدادی از این نقاط را در محاسبه کرده و در جدول زیر آورده‌ایم.

مثال سوم

برای تیتراسیون کاهشی $$U^{4+}$$ توسط $$Ce^{4+}$$ معادله‌ای بنویسید که پتانسیل نقطه هم‌ارزی را به دست بدهد. واکنش این اکسایش-کاهش به‌صورت زیر است.

$$\textrm{Ce}^{4+}(aq)+textrm U^{4+}(aq)\rightarrow \textrm{UO}_2^{2+}(aq)+textrm{Ce}^{3+}(aq)$$

پاسخ

برای رسیدن به پاسخ ابتدا باید نیم‌واکنش هر یک از گونه‌ها را یادداشت کنیم.

$$\textrm{Ce}^{4+}(aq)+e^-rightarrow \textrm{Ce}^{3+}(aq)$$

$$\mathrm{U^{4+}}(aq)+mathrm{2H_2O}\rightarrow \mathrm{UO_2^{2+}}(aq)+mathrm{4H^+}(aq)+2e^-$$

رابطه نرنست برای هر یک از نیم‌واکنش‌های بالا به‌‌صورت زیر است.

$$E=E^{\circ}\mathrm{_{Ce^{4+}/Ce^{3+}}-dfrac{0.05916}{1}logdfrac{[Ce^{3+}]}{[Ce^{4+}]}}$$

$$E=E^{\circ}\mathrm{_{UO_2^{2+}/U^{4+}}-dfrac{0.05916}{2}logdfrac{[U^{4+}]}{[UO_2^{2+}][H^+]^4}}$$

پیش از جمع بستن دو رابطه با یکدیگر، باید رابطه دوم را در عدد ۲ ضرب کنیم. این کار را به‌صورت زیر انجام می‌دهیم.

$$3E=E^{\circ}\mathrm{_{Ce^{4+}/Ce^{3+}}}+2E^{\circ}\mathrm{_{UO_2^{2+}/U^{4+}}-0.05916logdfrac{[Ce^{3+}][U^{4+}]}{[Ce^{4+}][UO_2^{2+}][H^+]^4}}$$

همچنین در نقطه هم‌ارزی این دو رابطه برقرار هستند.

$$\mathrm{[Ce^{3+}]=2times[UO_2^{2+}]}$$

$$\mathrm{[Ce^{4+}]=2times[U^{4+}]}$$

بعد از جایگذای این دو رابطه در رابطه بالا و انجام بازآرایی، معادله‌ای که نشان‌دهنده پتانسیل در نقطه هم‌ارزی باشد به‌صورت زیر به دست می‌آید.

$$3E=E^{\circ}\mathrm{_{Ce^{4+}/Ce^{3+}}}+2E^{\circ}\mathrm{_{UO_2^{2+}/U^{4+}}-0.05916logdfrac{2[UO_2^{2+}][U^{4+}]}{2[U^{4+}][UO_2^{2+}][H^+]^4}}$$

$$E=\dfrac{E^{\circ}_mathrm{Ce^{4+}/Ce^{3+}}+2E^{\circ}_mathrm{UO_2^{2+}/U^{4+}}}{3}-dfrac{0.05916}{3}logdfrac{1}{[\textrm H^+]^4}$$

$$E=\dfrac{E^{\circ}_mathrm{Ce^{4+}/Ce^{3+}}+2E^{\circ}_mathrm{UO_2^{2+}/U^{4+}}}{3}+dfrac{0.05916times4}{3}\log[\textrm H^+]$$

$$E=\dfrac{E^{\circ}_mathrm{Ce^{4+}/Ce^{3+}}+2E^{\circ}_mathrm{UO_2^{2+}/U^{4+}}}{3}-0.07888textrm{ pH}$$

در مقدار $$pH$$ برابر با ۱، پتانسیل نقطه هم‌ارزی را محاسبه می‌کنیم.

$$E_textrm{eq}=\dfrac{1.72 + 2times0.327}{3}-0.07888times1=0.712textrm{ V}$$

مثال چهارم

از تیتراسیون منگانومتری برای محاسبه میزان خلوص نمونه‌ای از سدیم اگزالات استفاده شده است. اگر برای تیتراسیون تا نقطه هم‌ارزی با ۳۵٫۶۲ میلی‌لیتر از پتاسیم پرمنگنات ۰٫۰۴ مولار، ۰٫۵۱۱۶ گرم از نمونه مصرف شود، درصد جرمی $$Na_2C_2O_4$$ را محاسبه کنید.

پاسخ

از آنجا که معادله موازنه شده این واکنش در سوال آورده نشده است، می‌توانیم با توجه به بار دو طرف به استوکیومتری این واکنش اکسایشی-کاهشی پی ببریم.

اکسایش گونه $$C_2O_4^{2-}$$ که در آن کربن دارای عدد اکسایش ۳+ است، به $$CO_2$$ با کربن دارای عدد اکسایش ۴+، نیازمند یک الکترون به ازای هر کربن است. در واقع به ازاری هر مول $$C_2O_4^{2-}$$ نیازمند ۲ عدد الکترون است. همچنین کاهش $$MnO_4^-$$ با منگنز دارای عدد اکسایش ۷+ به $$Mn^{2+}$$، نیازمند ۵ عدد الکترون است. بنابراین باید به ازاری هر دو مول پتاسیم پرمنگنات (۱۰ مول الکترون)، ۵ مول $$Na_2C_2O_4$$ یا ۱۰ مول الکترون شرکت داشته باشد.

تعداد مول‌های پتاسیم پرمنگنات مورد استفاده را می‌توان به‌صورت زیر محاسبه کرد.

$$\mathrm{(0.0400\;M\;KMnO_4)\times(0.03562\;L\;KMnO_4)=1.42times10^{-3}\;mol\;KMnO_4}$$

در این صورت مول‌های نمونه را نیز خواهیم داشت.

$$\mathrm{1.42times10^{-3}\;mol\;KMnO_4timesdfrac{5\;mol\;Na_2C_2O_4}{2\;mol\;KMnO_4}=3.55times10^{-3}\;mol\;Na_2C_2O_4}$$

با داشتن مول‌های سدیم اگزالات، درصد جرمی آن به شکل زیر قابل محاسبه است.

$$\mathrm{3.55times10^{-3}\;mol\;Na_2C_2O_4timesdfrac{134.00\;g\;Na_2C_2O_4}{mol\;Na_2C_2O_4}=0.476\;g\;Na_2C_2O_4}$$

$$\mathrm{\dfrac{0.476\;g\;Na_2C_2O_4}{0.5116\;g\;sample}times100=93.0%\;w/w\;Na_2C_2O_4}$$

درصد جرمی سدیم اگزالات در نمونه برابر با ۹۳٪ است.

حل تمرین از منگانومتری

در بخش پایانی تعدادی تمرین چند‌گزینه‌ای را مرور خواهیم کرد.

تمرین اول

 

تمرین دوم

 

سوالات متداول

حال که با مفهوم تیتراسیون منگانومتری آشنا شدیم، می‌خواهیم برخی از مهم‌ترین سوالاتی که پیرامون این موضوع وجود دارد را پاسخ دهیم.

تیترانت در تیتراسیون منگانومتری چیست ؟

در تیتراسیون منگانومتری از محلول پتاسیم پرمنگنات با غلظت مشخص به عنوان تیترانت استفاده می‌شود.

منحنی منگانومتری بر چه اساسی رسم می‌شود ؟

در این منحنی هر نقطه نشان‌دهنده پتانسیل واکنشی است که با افزودن حجم مشخصی از تیترانت به وجود می‌آید.

آیا در منگانومتری نیاز به شناساگر داریم ؟

خیر، منگانومتری از جمله روش‌های تیتراسیونی است که در آن نیازی به داشتن شناساگر برای تشخیص نقطه هم‌ارزی وجود ندارد زیرا حالت اکسایشی و کاهشی پتاسیم پرمنگنات دارای دو رنگ متفاوت است. البته در صورتی که غلظت پتاسیم پرمنگنات ناچیز باشد، می‌توان برای افزایش دقت از شناساگر تیتراسیون مناسب بهره برد.

در چه نقطه ای از تیتراسیون، پتانسیل نیم‌ واکنش کاهشی و اکسایشی با یکدیگر برابر خواهد بود ؟

در نقطه هم‌ارزی تیتراسیون پتانسیل نیم‌واکنش کاهشی و اکسایشی با هم برابر است.

جمع‌ بندی

هدف از این مطلب این بود که بدانیم تیتراسیون منگانومتری چیست و چگونه انجام می‌شود. این تیتراسیون به خانواده تیتراسیون‌های کاهشی تعلق دارد و در آن غالبا نیازی به استفاده از شناساگر برای تشخیص نقطه هم‌ارزی نیست، زیرا پتاسیم پرمنگنات در حالت اکسایشی و کاهشی خود دارای دو رنگ متفاوت است. در ادامه با بررسی تعدادی مثال و تمرین درک خود را از این مفهوم بیش‌تر کردیم و توانایی حل مسائلی برای یافتن غلظت آنالیت در تیتراسیون را به دست آوردیم.