فرادرسپتانسیل استاندارد در الکتروشیمی — از صفر تا صد
در یک سلول گالوانی، زمانیکه الکترون‌ها در خارج از سلول بوسیله سیم الکتریکی مدار، از آند به کاتد جریان پیدا می‌کنند، این جریان به دلیل اختلاف در انرژی پتانسیل بین دو الکترود در سلول الکتروشیمیایی بوجود می‌آید. در مباحث گذشته «مجله فرادرس»، مطالبی در خصوص پتانسیل سلول الکتروشیمیایی مطرح شد. در این مطلب قصد داریم تا به طور ویژه به پتانسیل استاندارد در سلول الکتروشیمیایی بپردازیم.
در سلول الکتروشیمیایی روی مس (سیستم Zn/Cu)، الکترون‌های لایه ظرفیت در روی (Zn)، انرژی پتانسیل بیشتری از الکترون‌های لایه ظرفیت در مس دارند چراکه در الکترون‌های لایه ظرفیت روی، اثر پوششی الکترون‌های S را بر روی اوربیتال پر شده d داریم. بنابراین، الکترون‌ها به طور خود به خودی از روی به طرف یون‌های مس (II) حرکت می‌کنند و یون‌های روی (II) و فلز مس را تشکیل می‌دهند. همانطور که با جریان خودبه‌خودی آب از بالا به پایین می‌توان یک چرخ چاه یا چرخ آبی را حرکت داد، جریان الکترون‌ها از انرژی پتانسیل بالاتر به پایین‌تر نیز می‌تواند برای انجام کار، مورد استفاده قرار بگیرد.
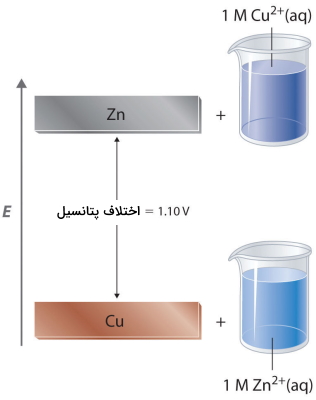
از آن‌جایی که انرژی پتانسیل الکترون‌های لایه ظرفیت از ماده‌ای به ماده دیگر تفاوت دارند، ولتاژ سلول گالوانی تا بخشی به ماهیت مواد شرکت کننده در واکنش وابسته است. اگر سلولی گالوانی را مشابه با تصویر بالا ایجاد کنیم اما به جای نوار مسی از فلز کبالت و محلول ۱ مولار $$Co ^ {2+}$$ در بخش کاتد بهره بگیریم، ولتاژ اندازه‌گیری شده به جای ۱/۱۰ ولت، برابر با ۰/۵۱ ولت خواهد بود. بنابراین می‌توانیم به این نتیجه برسیم که اختلاف در انرژی پتانسیل بین الکترون‌های لایه ظرفیت کبالت و روی، کمتر از اختلاف بین الکترون‌های ظرفیت مس و روی است و این اختلاف، مقداری برابر با 0/59 ولت دارد.
پتانسیل اندازه‌گیری شده سلول، همچنین به شدت به غلظت ذرات واکنش‌دهنده و دمای سیستم وابسته است. برای اینکه یک مقایس نسبی را توسعه دهیم که به کمک آن بتوانیم جهت یک واکنش الکتروشیمیایی و مقدار نیروی محرکه را پیش‌بینی کنیم، باید پتانسیل اکسایش و کاهش مواد مختلف را در شرایطی مشخص اندازه‌گیری کنیم و یک مقدار مرجع داشته باشیم. شیمیدان‌ها برای این کار از پتانسیل استاندارد سلول $$(E ^ \circ _ {cell})$$ استفاده می‌کنند.
پتانسیل استاندارد سلول چیست؟
پتانسیل استاندارد سلول به صورت پتانسیل یک سلول تحت شرایط استاندارد تعریف می‌شود. این بدان معنی است که تمامی ذرات در حالت استاندارد خود هستند. بنابراین، توجه داشته باشید که پتانسیل اکسایش کاهش به انرژی پتانسیل الکترون‌های لایه ظرفیت، غلظت ذرات در واکنش و دمای سیستم وابسته است.
اندازه گیری پتانسیل استاندارد الکترود
به طور فیزیکی نمی‌توان پتانسیل یک الکترود تنها را اندازه‌گیری کرد بلکه تنها می‌توانیم اختلاف پتانسیل بین دو الکترود را اندازه‌گیری کنیم. این مورد، شبیه به اندازه‌گیری انرژی آزاد یا آنتالپی است چراکه در آن مورد نیز تنها می‌توانستیم اختلاف این مقادیر را محاسبه کنیم. با این حال، می‌توان پتانسیل استاندارد را بین دو الکترود با یکدیگر مقایسه کرد که در این صورت، باید یک الکترود مشترک (مرجع) برای مقایسه داشته باشیم. با این کار، اختلاف پتانسیل بین دو الکترود مشابه، اندازه‌گیری خواهد شد.
به طور مثال، مقدار اندازه‌گیری شده پتانسیل استاندارد برای سیستم روی-مس برابر با 1/10 ولت است در حالیکه $$E ^ \circ$$ برای سیستم کبالت-روی، مقداری برابر با 0/51 ولت دارد. این مورد مشخص می‌کند که اختلاف پتانسیل بین الکترودهای کبالت و مس برابر با $$1.10 V − 0.51 V = 0.59 V$$ است. در حقیقت، اگر در شرایط استاندارد، دیاگرام سلولی مشابه زیر داشته باشیم، مقدار پتانسیل اندازه‌گیری شده آن دقیقا با مقدار 0/59 ولت برابر است.
$$C o_{(s)} ∣ Co^{2+} (aq, 1 M)∥Cu^{2+}(aq, 1 M) ∣ Cu (s)\;\;\; E°=0.59\; V$$
این دیاگرام سلول متناظر با اکسایش آند کبالت و کاهش $$Cu ^ {2+}$$ در محلول و در کاتد مس است. تمامی مقادیر فهرست‌شده پتانسیل‌های الکترود استاندارد، به طور معمول، به صورت کاهشی نوشته می‌شوند تا بتوان آن‌ها را با پتانسیل استاندارد سایر مواد، مقایسه کرد. بنابراین، پتانسیل استاندارد سلول برابر با اختلاف بین پتانسیل‌های کاهشی دو نیم‌واکنش است که آن‌را به صورت اختلاف پتانسیل استاندارد کاتد منهای آند تعریف می‌کنند.
$$E°_{cell} = E°_{cathode} − E°_{anode} $$
در مقابل، به یاد دارید که نیم واکنش‌ها برای نشان دادن واکنش‌های اکسایش و کاهش بکار می‌روند که در داخل سلول انجام می‌شوند. بنابراین، واکنش کلی سلول را به صورت مجموع دو نیم‌واکنش می‌نویسند. بر اساس رابطه بالا، زمانی که پتانسیل استاندارد را برای هر نیم‌واکنش داشته باشیم، می‌توانیم مقدار پتانسیل استاندارد بسیاری از نیم‌واکنش‌های دیگر را با اندازه‌گیری پتاسیل استاندارد سلول متناظر آن، بدست آوریم.
توجه داشته باشید که واکنش کلی در سلول، برابر با مجموع دو نیم‌واکنش است اما پتانسیل سلول، به اختلاف بین پتانسیل‌های کاهش می‌گویند.
الکترود استاندارد هیدروژن
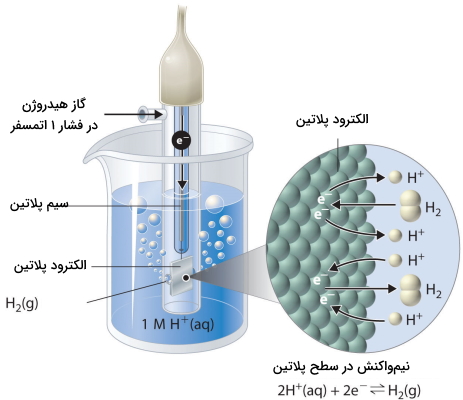
با وجود اینکه نمی‌توان پتانسیل هر الکترود را به طور مستقیم محاسبه کرد، اما همانطور که گفته شد، از یک الکترود مرجع برای این کار بهره می‌گیریم که و پتانسیل آن‌را در شرایط استاندارد، صفر ولت تعریف می‌کنیم. «الکترود استاندارد هیدروژن» (Standard Hydrogen Electrode) یا (SHE) به همین منظور استفاده می‌شود. این الکترود شامل نواری از پلاتین، در تماس با محلول آبی یک مولار از $$H ^ +$$ است. $$H ^ +$$ در محلول، در تعادل با گاز $$H _ 2$$ در فشار ۱ اتمسفر قرار دارد.
بر طبق واکنش زیر، در سطح پلاتین، پروتون‌ها کاهش می‌یابند یا به عبارت دیگر، مولکول‌های هیدروژن اکسید می‌شوند.
$$2 H^+_{(aq)} +2e^− \rightleftharpoons H_ {2 (g)}$$
یکی از ویژگی‌های جذاب SHE این است که الکترود پلاتین، در طول واکنش، مصرف نمی‌شود.
تصویر زیر یک سلول گالوانی را نشان می‌دهد که شامل SHE در یک بشر و نواری از جنس روی (Zn) در بشر دیگر و حاوی محلولی از یون‌های $$Zn ^ {2+}$$ است. زمانیکه مدار بسته شود، ولت‌متر، پتانسیل 0/76 ولت را نشان می‌دهد. الکترود روی شروع به حل شدن و تشکیل یون $$Zn ^ {2+}$$ می‌کند و یون‌های $$H ^ +$$ در طرف دیگر به $$H _ 2$$ تبدیل می‌شوند.
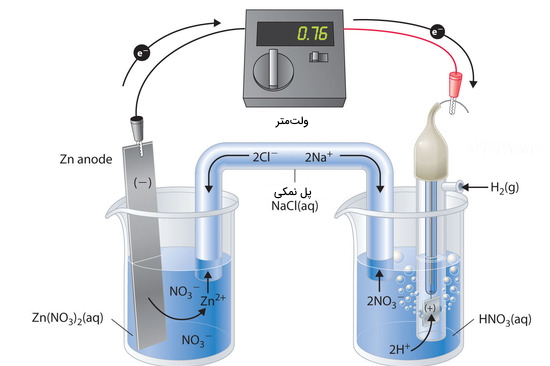
بنابراین، کاتد در اینجا، الکترود هیدروژن و آند، الکترود روی است. دیاگرام این سلول گالوانی در زیر آورده شده است:
$$Zn _ {(s)} ∣ Z n ^{2 + }_ {(a q )}∥ H ^+(aq, 1 M)∣ H _ 2(g, 1 atm )∣ P t _{(s)}$$
در زیر، نیم‌واکنش‌های سلول و الکترودهای مربوطه، آورده شده است:
نیم‌واکنش کاتد: $$2 H^+_{(aq)} + 2e^− \rightarrow H_ {2(g)}\;\;\; E° _{cathode} =0 V $$
نیم‌واکنش آند: $$Z n _ {(s)} \rightarrow Z n ^ {2+} _ {(aq)} + 2e^−\;\;\; E°_ {anode}= −0.76\; V $$
واکنش کلی: $$Z n _{(s)} + 2 H^+_{(aq)} \rightarrow Z n ^{2+}_ {(a q)} +H _ {2(g)}$$
$$E° _ {cell} = E°_ {cathode}− E°_{anode}= 0.76\; V$$
با وجود اینکه واکنش در آند، اکسایشی است اما به طور معمول، آن‌را در جداول به صورت پتانسیل کاهشی گزارش می‌کنند. به پتانسیلی در نیم‌واکنش که تحت شرایط استاندارد و در برابر SHE اندازه‌گیری شود، «پتانسیل استاندارد الکترود» (Standard Electrode Potential) آن واکنش می‌گویند.
در این مثال، پتانسیل استاندارد کاهش برای $$\mathrm {Z n}^ {2+}(\mathrm {a q})+2 \mathrm{ e}^{-} \rightarrow \mathrm{ Z n} (\mathrm{s})$$ برابر با $$-0.76$$ ولت است یعنی پتانسیل الکترود استاندارد برای این واکنش در آند رخ می‌دهد. اکسایش $$Zn$$ به $$Zn ^ {2+}$$ را به طور معمول، جفت اکسایش کاهش $$Zn/Zn ^ {2+}$$ می‌نامند. برای بدست آوردن $$E ^ \circ _{cell}$$ نیز از رابطه زیر استفاده می‌کنیم:
$$\begin {equation} \mathrm {E}_{\text {cell }}^{\circ}: 0-(-0.76 \mathrm{V})=0.76 \mathrm{V}\end{equation}$$
از آن‌جایی که پتانسیل الکتریکی به انرژی مورد نیاز برای حرکت دادن یک ذره باردار در یک میدان الکتریکی می‌گویند، پتانسیل استاندارد الکترود برای نیم‌واکنش‌ها، از جمله خواص شدتی به شمار می‌آید و وابسته به مقدار ماده موجود نیست. در نتیجه، مقادیر $$E ^ \circ$$، مستقل از ضرایب استوکیومتری نیم‌واکنش هستند و مهم‌تر اینکه ضرایبی که بمنظور ایجاد یک معادله موازنه شده استفاده می‌شوند، تاثیری بر مقدار پتانسیل سلول نخواهند داشت. از گفته‌های بالا به یک نکته مهم می‌رسیم:
به دلیل اینکه پتانسیل استاندارد، خاصیتی شدتی است، مقادیر $$E ^ \circ$$ به ضرایب استوکیومتری وابسته نیستند.
پتانسیل استاندارد الکترود
برای اندازه‌گیری پتانسیل جفت $$Cu / Cu ^{2+}$$، می‌توانیم یک سلول گالوانی مانند تصویر قبل بسازیم که به جای $$Zn/Zn ^ {2+}$$، شامل جفت $$Cu / Cu ^{2+}$$ باشد. این بار، با بسته شدن مدار، پتانسیل اندازه‌گیری شده برای سلول، عدد $$-0.34 V$$ خواهد بود که عددی منفی است. مقدار منفی $$E ^ \circ _{cell}$$ نشان می‌دهد جهت جریان خودبه‌خودی الکترون‌ها، بر خلاف جفت $$Zn/Zn ^ {2+}$$ است. بنابراین، واکنش‌هایی که به صورت خودبه‌خودی روی می‌دهند، با $$E ^ \circ _{cell}$$ مثبت مشخص خواهند شد که در اینجا، کاهش $$Cu ^{2+}$$ به $$Cu$$ در الکترود مس خواهد بود.
با پیشرفت واکنش، بر جرم الکترود مس، افزوده می‌شود و در الکترود پلاتین، $$H _ 2$$ به $$H ^ +$$ اکسید می‌شود. در این سلول، مس، کاتد و الکترود هیدروژن، آند است. بنابراین، نحوه نوشتن دیاگرام سلول، به صورت زیر خواهد بود که در آن، SHE در چپ و جفت $$Cu / Cu ^{2+}$$ در راست، آورده شده‌اند.
$$Pt_{(s)}∣H_2(g, 1 atm)∣H^+(aq, 1\; M)∥Cu^{2+}(aq, 1 M)∣Cu_{(s)}$$
نیم‌واکنش‌ها و پتانسیل‌های واکنش خودبه‌خودی در زیر آورده شده است:
کاتد: $$C u ^ {2 +} {(aq)} + 2 e^− \rightarrow C u_{(g)}\;\;\; E ° _ {cathode} = 0.34\; V$$
آند: $$H _{2(g)} \rightarrow 2 H ^+_ {(aq)} + 2 e^−\;\;\; E°_ {anode} = 0\; V$$
واکنش کلی: $$H_{2(g)} + Cu^{2+}_{(aq)} \rightarrow 2H^+_{(aq)} + Cu_{(s)}$$
$$E°_ {cell} = E°_ {cathode}− E° _{anode} = 0.34\; V$$
بناراین، پتانسیل استاندارد الکترود برای جفت $$Cu / Cu ^{2+}$$، برابر با 0/34 ولت خواهد بود.
محاسبه پتانسیل استاندارد سلول
پتانسیل استاندارد برای یک واکنش ردوکس، معیاری از تمایل واکنش‌دهنده‌ها در حالت استاندارد، برای تشکیل فرآورده در حالت استاندارد است. بنابراین، به نوعی «نیروی محرکه» (Driving Force) واکنش قلمداد می‌شود که این نیروی محرکه را با ولتاژ توصیف کردیم. با استفاده از دو پتانسیل استاندارد الکترودی که پیش‌تر بدست آوردیم، می‌توان پتانسیل استاندارد برای سلول الکتروشیمیایی روی مس را بدست آوریم که دیاگرام سلول آن به صورت زیر است:
$$Z n{(s)}∣Z n^{2+}(aq, 1 M)∥C u^{2+}(aq, 1 M) ∣Cu_{(s)} $$
مقادیر $$E°$$ را برای آند و کاتد داریم و بنابراین، مقدار $$E°_ {cell}$$ را محاسبه خواهیم کرد.
کاتد: $$C u^{2+}_{(aq)} + 2e^− \rightarrow Cu_{(s)} \;\;\; E°_{cathode} = 0.34\; V$$
آند: $$Z n_{(s)} \rightarrow Zn^{2+} (aq, 1 M) + 2e^−\;\;\; E°_ {anode} = −0.76\; V $$
واکنش کلی: $$Zn_{(s)} + Cu^{2+}_{(aq)} \rightarrow Zn^{2+}_{(aq)} + Cu_{(s)} $$
$$E° _{cell} = E°_ {cathode} − E°_ {anode} = 1.10\; V$$
عدد بدست آمده با مقدار آزمایشگاهی آن مطابقت دارد. اگر مقدار $$E°_ {cell}$$ مثبت باشد، واکنش به طور خودبه‌خودی به همان شکل معادله واکنش، انجام می‌گیرد و اگر این مقدار، منفی باشد، این واکنش، خوبه‌خودی نخواهد بود و تحت شرایط استاندارد، بر اساس معادله بالا انجام نمی‌گیرد و انجام آن، در جهت مخالف امکان‌پذیر است.
البته مقدار منفی به آن معنی نیست که نتوان کاری کرد که واکنش به جهت دلخواه ما انجام بگیرد. اگر به میزان کافی از انرژی الکتریکی استفاده کنیم، به این هدف دست پیدا می‌کنیم.
مثال محاسبه پتانسیل استاندارد
یک سلول گالوانی با میزان پتانسیل استاندارد سلول 0/27 ولت را به کمک دو بشر و یک پل نمکی تهیه کرده‌ایم. یک بشر حاوی نواری از فلز گالیم در محلول ۱ مولار $$GaCl_3$$ و دیگری شامل قطعه‌ای از فلز نیکل در محلول ۱ مولار از $$NiCl_2$$ است. نیم‌واکنش‌ها بعد از اتصال دو بخش به یکدیگر، به صورت زیر خواهند بود:
کاتد: $$\begin {equation}\mathrm{ Ni}^{2+}(\mathrm {aq})+2 \mathrm{e}^{-} \rightarrow \mathrm {Ni}(\mathrm{s})\end {equation}$$
آند: $$\begin {equation} \mathrm{ Ga} (\mathrm{s}) \rightarrow \mathrm {Ga} ^{3+} (\mathrm {aq})+3 \mathrm {e}^{-} \end {equation}$$
اگر پتانسیل اکسایش $${Ga} ^{3+}$$ تحت شرایط استاندارد، برابر با 0/55 ولت باشد، پتانسیل اکسایش $$Ni$$ به $$Ni^ {2+}$$ چقدر است.
برای حل این سوال، به روش زیر عمل می‌کنیم:
- معادله نیم‌واکنش در آند را به همراه مقدار پتانسیل استاندارد الکترود آن می‌نویسیم.
- از رابطه‌ای که داشتیم، مقدار پتانسیل استاندارد الکترود برای نیم واکنش کاتد را محاسبه می‌کنیم و سپس، علامت آن‌را برای بدست آوردن نیم‌واکنش اکسایش، قرینه می‌کنیم.
پتانسیل اکسایش $${Ga} ^{3+}$$ به $$Ga$$ را تحت شرایط استاندارد داریم اما برای استفاده، باید علامت آن قرینه شود. در نتیجه، برای نیم‌واکنش کاهش، خواهیم داشت:
$$\begin {equation} \mathrm {Ga} ^{ 3+} (\mathrm{aq}) + 3 \mathrm{e} ^ {-} \rightarrow \mathrm{Ga} (\mathrm{s}), \mathrm {E} ^ {\circ} \text { anode } = -0.55 \mathrm { V } \end {equation}$$
با مقادیر داده شده برای $$E°_ {cell}$$ و مقادیر محاسبه شده $$E \circ _ {anode}$$، می‌توانیم مقدار پتانسیل استاندارد برای کاهش $$N i ^ {2+}$$ به $$Ni$$ را حساب کنیم:
$$\begin{equation}
\begin{array}{c}
\mathrm{E}^ {\circ} \mathrm {cell} = \mathrm { E}^ {\circ} \text { cathode } - \mathrm{E} ^ {\circ} \text { anode } \\
0.27 \mathrm {V} = \mathrm {E}^ {\circ} \text { cathode }-(-0.55 \mathrm{V}) \\
\mathrm {E} ^ {\circ} \text { cathode } = -0.28 \mathrm{V}
\end {array}
\end {equation}$$
این مقدار محاسبه شده، پتانسیل استاندارد الکترود برای واکنش $$\mathrm {N i}^ {2+} (\mathrm {aq}) +2 \mathrm {e}^{-} \rightarrow \mathrm {Ni} (\mathrm {s})$$ است. از آن‌جایی که می‌خواهیم پتانسیل اکسایش $$Ni$$ به $$N i ^ {2+}$$ را تحت شرایط استاندارد حساب کنیم، باید علامت $$E ^ \circ_ {cathode}$$ را قرینه کنیم. بنابراین، مقدار آن برابر با 0/28 ولت برای اکسایش خواهد بود. با نگاهی به معادله واکنش در می‌یابیم که ۳ الکترون (در فرآیند کاهش) مصرف و ۲ الکترون (در فرآیند اکسایش) تولید شده‌اند. بنابراین، این واکنش، موازنه نیست اما همانطور که در ابتدای متن نیز گفته شد، پتانسیل استاندارد، مستقل از ضرایب استوکیومتری است.
جدول پتانسیل استاندارد
با استفاده از روشی که توضیح داده شد، می‌توانیم پتانسیل استاندارد را برای گستره عظیمی از مواد شیمیایی بدست آوریم و مقادیر بدست آمده را همگی در یک جدول، فهرست کنیم.
نمونه‌ای از این فهرست، در انتهای مطلب «پتانسیل سلول — به زبان ساده» آورده شده است. این جدول به ما کمک می‌کند تا قدرت‌های اکسندگی و کاهندگی مواد بسیاری را با یکدیگر مقایسه کنیم. برای ارائه توضیحات بهتر، بخش بسیار کوچکی از این جدول در زیر آورده شده است.
| پتانسیل استاندارد | نیم‌واکنش |
| $$+0.17$$ | $$\mathrm{SO}_{4}^{2-}(\mathrm{aq})+4 \mathrm{H}^{+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow 2 \mathrm{H}_{2} \mathrm{O}(\mathrm{I})+\mathrm{SO}_{2}(\mathrm{g})$$ |
| $$+0.154$$ | $$\mathrm{Sn}^{4+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{Sn}^{2+}(\mathrm{aq})$$ |
| $$+0.14$$ | $$S(s)+2 H^{+}(a q)+2 e^{-} \rightarrow H_{2} S(g)$$ |
| $$0$$ | $$2 \mathrm{H}^{+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{H}_{2}(\mathrm{g})$$ |
| $$-0.125$$ | $$\mathrm{Pb}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{Pb}$$ |
| $$-0.137$$ | $$\mathrm{Sn}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{Sn}(\mathrm{s})$$ |
| $$-0.440$$ | $$\mathrm{Fe}^{2+}(\mathrm{aq})+2 \mathrm{e}^{-} \rightarrow \mathrm{Fe}(\mathrm{s})$$ |
| $$-0.763$$ | $$\mathrm{Zn}^{2+}+2 \mathrm{e}^{-} \rightarrow \mathrm{Zn}(\mathrm{s})$$ |
تمامی واکنش‌دهنده‌های بالای SHE، اکسنده‌های قوی‌تری نسبت به $$H ^ +$$ هستند و آن‌هایی که پایین‌تر از SHE قرار دارند، اکسنده‌های ضعیف‌تری هستند. به طور مثال، برای $$F _ 2$$، مقدار این پتانسیل برابر با 2/87 ولت است. این مقدار زیاد در تطابق با الکترونگاتیوی بالای فلوئور قرار دارد و این نکته را به ما گوشزد می‌کند که فلوئور، تمایل بیشتری برای پذیرش الکترون‌ها نسبت به سایر عناصر موجود در جدول تناوبی دارد.
از آن‌جایی که نیم‌واکنش‌های نشان داده شده در جدول بالا، همگی بر اساس مقادیر $$E ^ \circ$$ نوشته شده‌اند، به کمک جدول می‌توان به سرعت، قدرت نسبی اکسنده‌ها و کاهنده‌های مختلف را پیش‌بینی کرد. هر ذره‌ای در سمت چپ نیم‌واکنش، به طور خودبه‌خودی، هر ذره (جزء) در سمت راست نیم‌واکنش دیگر را اکسید می‌کند به شرطی که بالاتر از آن در جدول قرار گرفته باشد. برای توضیح بیشتر این مطلب، مثال زیر را مطرح می‌کنیم.
مثال استفاده از جدول پتانسیل استاندارد
لکه‌های تیره بوجود آمده بر روی سطوح ساخته شده از نقره، به طور معمول از $$Ag_2S$$ تشکیل شده‌اند. نیم‌واکنش برای معکوس کردن این فرآیند در زیر آورده شده است:
$$\begin {equation}
\mathrm {Ag} _ {2} \mathrm { S} (\mathrm {s}) +2 \mathrm {e} ^ {-} \rightarrow 2 \mathrm {A g }( \mathrm{s}) + \mathrm{S } ^ {2-}(\text { aq }) \quad \mathrm {E} ^ {\circ} =-0.69 \mathrm {V}
\end {equation}$$
- با استفاده از جدول پتانسیل، پیش‌بینی کنید که کدامیک از مواد زیر، می‌توانند تحت شرایط استاندارد، $$Ag_2S$$ را به $$Ag$$ کاهش دهند.
- $$H_2 O_2 (aq)$$
- $$Zn (s)$$
- $$I ^ - (aq)$$
- $$Sn ^ {2+} (aq)$$
- به کمک هر یک از ترکیبات (ذرات) بالا، مشخص کنید که کدامیک از این ترکیبات، قوی‌ترین عامل کاهنده در محلول آبی به شمار می‌آید.
- با استفاده از جدول، عوامل کاهنده دیگری را پیشنهاد کنید که دسترسی آسان، قیمت کم و اثر بیشتری در حذف لکه‌ها داشته باشند.
این مثال را می‌توان از دو روش حل کرد: محل نسبی چهار کاهنده را با جفت $$Ag_2S / Ag $$ مقایسه کنیم یا اینکه مقدار $$E ^ \circ$$ را برای هر ذره با مقدار آن برای جفت $$Ag_2S / Ag $$ مقایسه کنیم که مقدار آن برابر با $$-0.69V$$ است.
جدول پتانسیل از پایین به بالا بر اساس افزایش قدرت کاهندگی مرتب شده است. از بین ذرات داده شده در مثال، تنها $$Zn (s)$$، بالاتر از $$Ag_2S$$ قرار دارد. بنابراین به این نتیجه می‌رسیم که تنها $$Zn (s)$$ می‌تواند $$Ag_2S$$ را تحت شرایط استاندارد، کاهش دهد.
همانطور که گفته شد، قوی‌ترین کاهنده، $$Zn (s)$$ است. محصولات تجاری که از قطعه‌ای از روی ساخته شده‌اند، به طور معمول نام «کالای معجزه‌گر» (Miracle Product) دارند چراکه برای حذف لکه‌های تیره، تنها کافی است آب گرم به همراه کمی نمک اضافه کنید تا لکه‌ها از بین بروند.
از بین سایر واکنش‌دهنده‌هایی که بالاتر از $$Zn (s)$$ قرار دارند و در نتیجه، کاهنده‌های قوی‌تری هم هستند، تنها یک مورد را می‌توان پیدا کرد که شرایط سوال را داشته باشد و آن، فویل آلومینیومی است که در بسته‌بندی مواد غذایی مورد استفاده قرار می‌گیرد و به خوبی و با قیمت پایین، در دسترس است.
سلام
پتانسیل کاهشی پلاتین ۱/۲ و پتانسیل کاهشی اکسیژن در محیط اسیدی ۱/۲۳ است پس قاعدتاً باید پلاتین در محیط اسیدی اکسید شود اما در کتاب شیمی دوازدهم آمده حتی در محیط اسیدی هم این واکنش رخ نمی دهد.
ممنون میشم جواب بدید.
سلام و روز به‌خیر به شما دوست عزیز؛
پلاتین نیز مانند طلا به دسته فلزهای نجیب تعلق دارد که با وجود میزان پتانیل کاهشی کمتر از اکسیژن، حتی در محیط‌های اسیدی نیز دچار اکسایش نمی‌شود.
خوشحالیم که ما مجله فرادرس همراه هستید.
سلام مهندس ممنون از مطالب خوبتون یه سوال دارم مهندس بنده از محلول تیزاب مقداری طلای گم شده دارم که می خوام از طریق الترولیز استخراجش کنم به نظر شما شما چه نو فلزی برای کاتد و انداستفاده کنم که بهم کمک بیشتری به استخراج طلا از محلول تیزابی کنه با چه ولتاژی ممنون میشم راهنمایم کنی. ممنون
با سلام؛
برای آشنایی با نحوه استخراج طلا، پیشنهاد می‌کنیم مطلب «استخراج طلا با سیانوراسیون — از صفر تا صد» را مطالعه کنید.
با تشکر از همراهی شما با مجله فرادرس