قاعده چیست؟ | قاعده در اشکال هندسی به زبان ساده

قاعده بخش خاصی از یک شکل هندسی است که از سایر بخش‌های آن شکل متمایز شده و در واقعیت یا از نظر تصویری در پایین یا کف تصویر یا جسم قرار می‌گیرد. در ادامه این آموزش از مجله فرادرس، با جزئیات بیشتری بیان می‌کنیم که قاعده چیست و در اشکال و احجام مختلف هندسی چگونه است.

قاعده چیست ؟

همان‌طور که گفتیم، «قاعده» یا «پایه» (Base) بخش خاصی از یک شکل هندسی است که از سایر بخش‌های آن شکل متمایز شده و معمولاً در پایین یا کف تصویر یا جسم قرار می‌گیرد و به همین دلیل قاعده یا پایه نام گرفته است.

در بعضی موارد قاعده از نظر کیفی با سایر قسمت‌های شکل متفاوت است.

قاعده چند ضلعی ها

برای یک چندضلعی دو بعدی مشخص، ممکن است هر یک از اضلاع آن به طور موقت از قسمت‌های دیگر متمایز و به عنوان قاعده در نظر گرفته شود. معمول این است که چند ضلعی طوری رسم شود که قاعده به صورت افقی و در پایین شکل قرار گیرد.

فیلم آموزش هندسه پایه دهم – هندسه ۱ در فرادرس

کلیک کنید

قاعده قطعه‌ای از دایره

قاعده یک قطعه از یک دایره، پاره‌خط مستقیمی است که یکی از مرزهای آن قسمت را تشکیل می‌دهد. در شکل زیر، AB قاعده قطعه دایره زرد بوده که در تصویر مشخص شده است.

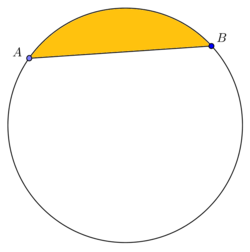
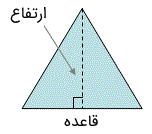
قاعده مثلث

قاعده‌‌ یکی از اضلاع چندضلعی است که معمولاً به عنوان ضلع مرجع برای اندازه‌گیری‌های دیگر استفاده می‌شود. قاعده‌ مثلث را اغلب در محاسبه مساحت آن می‌بینیم.

 یک روش معمول برای محاسبه مساحت مثلث، حاصل‌ضرب نصف قاعده در ارتفاع است که در آن، «ارتفاع» فاصله عمود از قاعده‌ تا رأس مقابل آن است.

قاعده متوازی الاضلاع

اگر چهار ضلعی دارای یک جفت ضلع موازی باشد، هر دو آن‌ها دو ضلع را قاعده‌ می‌نامند. و دقیقاً مثل مثلث، ارتفاع چنین شکلی فاصله عمودی از یک قاعده‌ تا قاعده مقابل است. می‌توان هر دو قاعده‌ را به عنوان نقطه شروع انتخاب کرد. به عنوان مثال، در یک متوازی‌الاضلاع شکل زیر را داریم.

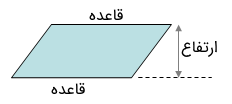
قاعده‌های لوزی، ذوزنقه و... نیز همین‌گونه تعریف می‌شوند.

قاعده‌ احجام سه بعدی

قاعده یک شکل فضایی یکی از وجه‌های آن است که به گونه‌ای از سایر وجوه متمایز شده است. شکل فضایی معمولاً به گونه‌ای است که قاعده‌ در کف آن قرار می‌گیرد.

قاعده متوازی السطوح

یکی از وجوه موازی به طور دلخواه انتخاب شده و از سایر وجه‌ها متمایز و به صورت قاعده‌ در نظر گرفته می‌شود. معمولاً انتخاب قاعده‌ به صورتی است که در کف قرار دارد. در شکل زیر، ABCD به طور متعارف به عنوان قاعده‌ شناخته می‌شود.

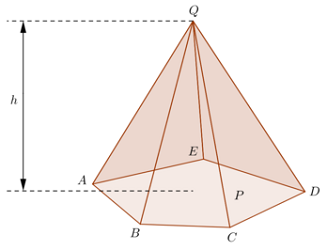
قاعده هرم

یک چند ضلعی از هرمی که رئوس آن به هم متصل است، قاعده‌ هرم نامیده می‌شود. در شکل زیر، ABCDE قاعده هرم ABCDEQ است.

قاعده منشور

قاعده‌های منشور دو چندضلعی موازی هستند که وجوه را در دو انتهای منشور تشکیل میدهند. در شکل زیر، وجه‌های ABCDE و FGHIJ قاعد‌ه‌های منشور هستند.

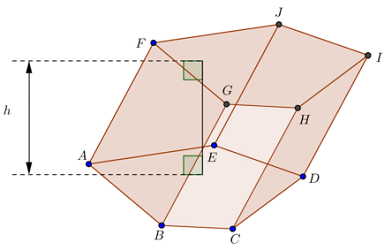
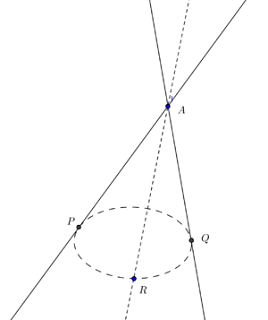
قاعده مخروط

صفحه PQR را قاعده‌ مخروط زیر می‌نامند. برای مخروط قائم نیز همین‌گونه است.

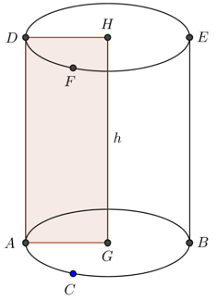
قاعده استوانه

دو وجه ABC و DEF قاعده‌های استوانه زیر هستند.

برای یادگیری اشکال مختلف هندسی و محاسبه محیط، مساحت و حجم آن‌ها، توصیه می‌کنیم آموزش‌های مجله فرادرس را که در این زمینه تهیه شده‌اند، مطالعه کنید: