فرادرس
فرمول های محیط و مساحت اشکال هندسی (+ فیلم و PDF رایگان)
قبلاً در مجموعه آموزشهای مجله فرادس با اشکال هندسی و فرمول های محیط و مساحت آن‌ها آشنا شدیم و مثال‌های متنوعی را نیز حل کردیم. در این آموزش، فرمول های محیط و مساحت اشکال هندسی را مرور می‌کنیم.
فرمول های محیط و مساحت اشکال هندسی
در ادامه، فرمول های محیط و مساحت و حجم اشکال هندسی را بیان می‌کنیم.
فرمول های محیط و مساحت دایره
دایره زیر را در نظر بگیرید.
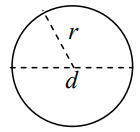
فرمول مساحت دایره
مساحت دایره‌ای به شعاع $$r$$ برابر است با:
$$ \large \boxed {A = \pi r ^ 2 } $$
مساحت دایره‌ای به قطر $$ d $$ به صورت زیر است:
$$ \large \boxed {A = \pi \frac {d ^ 2 }{4}} $$
برای آشنایی بیشتر با محاسبه مساحت دایره و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «مساحت دایره — به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید.
فرمول محیط دایره
محیط دایره‌ای به شعاع $$r $$ برابر است با:
$$ \large \boxed {P = 2 \pi r } $$
محیط یک دایره به قطر $$d$$ به صورت زیر است:
$$ \large \boxed {P = \pi d } $$
برای آشنایی بیشتر با محاسبه محیط دایره و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «محیط دایره — به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید.
فرمول های محیط و مساحت مثلث
مثلث زیر را در نظر بگیرید.
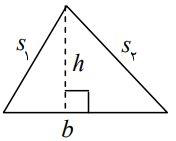
فرمول مساحت مثلث
مساحت مثلثی به ارتفاع $$h$$ و قاعده $$b $$ به شکل زیر است:
$$ \large \boxed {A = \frac 12 \times b \times h } $$
برای آشنایی بیشتر با محاسبه مساحت مثلث و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «مساحت مثلث — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.
فرمول محیط مثلث
محیط مثلث با ساق‌های $$s_1$$ و $$s_2$$ و قاعده $$b$$ برابر است با:
$$ \large \boxed {P = s_1 + s_ 2 + b} $$
برای آشنایی بیشتر با محاسبه محیط مثلث و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «محیط مثلث — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.
برای آشنایی بیشتر با فرمول های محیط و مساحت و حجم اشکال مختلف هندسی، پیشنهاد می‌کنیم به مجموعه فیلم‌های آموزش دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.
- برای مشاهده مجموعه فیلم‌های آموزش دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.
فرمول های محیط و مساحت مربع
مربع زیر را در نظر بگیرید.
فرمول مساحت مربع
مساحت مربعی به ضلع $$ s $$ برابر است با:
$$\large \boxed {A = s ^ 2 }$$
فرمول محیط مربع
اگر طول ضلع مربعی $$ s $$ باشد، محیط آن به صورت زیر خواهد بود:
$$\large \boxed {P = 4 s }$$
برای آشنایی بیشتر با محاسبه محیط مربع و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «محیط مربع و محاسبه آن | به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید.
فرمول های محیط و مساحت مستطیل
مستطیل زیر را داریم.
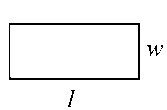
فرمول مساحت مستطیل
مساحت مستطیلی به طول $$ l $$ و عرض $$w $$ برابر است با:
$$ \large \boxed {A = l \times w} $$
برای آشنایی بیشتر با محاسبه مساحت مستطیل و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «مساحت مستطیل — به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید.
فرمول محیط مستطیل
محیط مستطیلی به طول $$ l $$ و عرض $$w $$ برابر است با:
$$ \large \boxed {P = 2 ( l + w)} $$
برای آشنایی بیشتر با محاسبه محیط مستطیل و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «محیط مستطیل و محاسبه آن — به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید.
فرمول های محیط و مساحت لوزی
لوزی زیر را در نظر بگیرید.
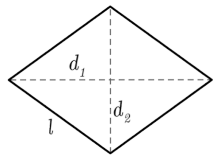
فرمول مساحت لوزی
مساحت یک لوزی با قطرهای $$ d _ 1 $$ و $$ d _ 2 $$ به صورت زیر است:
$$\large \boxed { A = \frac 12 d _ 1 d _ 2 }$$
برای آشنایی بیشتر با محاسبه مساحت لوزی و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «مساحت لوزی — به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید.
فرمول محیط لوزی
محیط یک لوزی به ضلع $$l$$ برابر است با:
$$\large \boxed { P = 4 l }$$
برای آشنایی بیشتر با محاسبه محیط لوزی و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «محیط لوزی — به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید.
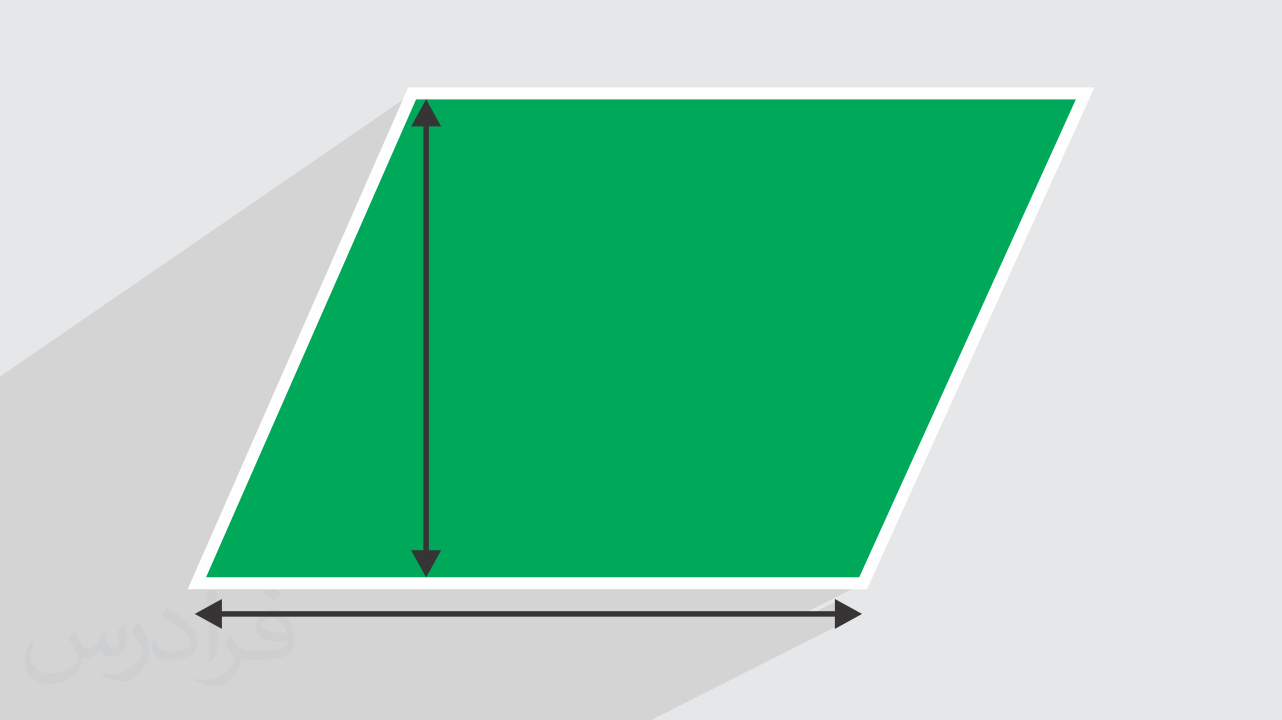
فرمول های محیط و مساحت متوازی الاضلاع
متوزی الاضلاع زیر را داریم.
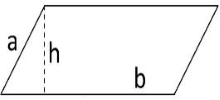
فرمول مساحت متوازی الاضلاع
مساحت متوازی‌الاضلاعی با ارتفاع $$h$$ و قاعده $$ b $$ برابر است با:
$$ \large \boxed {A = b \times h } $$
برای آشنایی بیشتر با محاسبه مساحت متوازی الاضلاع و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «مساحت متوازی الاضلاع و محاسبه آن | به زبان ساده» مراجعه کنید.
فرمول محیط متوازی الاضلاع
اگر دو ضلع متوالی یک متوازی‌الاضلاع برابر با $$a $$ و $$ b $$ باشند، محیط آن به صورت زیر محاسبه می‌شود:
$$ \large \boxed {P = 2 ( a + b ) } $$
برای آشنایی بیشتر با محاسبه محیط متوازی الاضلاع و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «محیط متوازی الاضلاع و محاسبه آن | به زبان ساده» مراجعه کنید.
فرمول های محیط و مساحت ذوزنقه
ذوزنقه زیر را در نظر بگیرید.
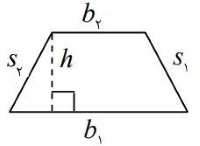
فرمول مساحت ذوزنقه
اگر ارتفاع ذوزنقه برابر با $$h $$ و قاعده‌های آن $$ b_1 $$ و $$ b_2 $$ و ساق‌هایش $$s_1$$ و $$s_ 2 $$ باشند، مساحت آن به صورت زیر به دست می‌آید:
$$ \large \boxed {A = \frac 1 2 h ( b _ 1 + b _ 2 ) } $$
برای آشنایی بیشتر با محاسبه مساحت ذوزنقه و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «محاسبه مساحت ذوزنقه — به زبان ساده» مراجعه کنید.
فرمول محیط ذوزنقه
محیط ذوزنقه‌ای با قاعده‌های $$ b_1 $$ و $$ b_2 $$ و ساق‌های $$s_1$$ و $$s_ 2 $$ برابر است با:
$$\large \boxed {P=s_1 + b_ 1 + s _2 + b _ 2}$$
برای آشنایی بیشتر با محاسبه محیط ذوزنقه و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «محیط ذوزنقه و محاسبه آن | به زبان ساده (+ فیلم آموزش رایگان)» مراجعه کنید.
فرمول های محیط و مساحت بیضی
بیضی زیر داده شده است.
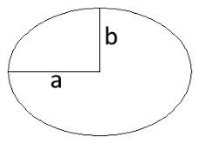
فرمول مساحت بیضی
مساحت یک بیضی با قطر کوچک $$b$$ و قطر بزرگ $$ a $$ به صورت زیر به دست می‌آید:
$$\large \boxed {A = \pi a b }$$
فرمول محیط بیضی
محیط تقریبی بیضی برابر است با:
$$\large \boxed {P = 2 \pi \sqrt {\frac {a^2+b^2}2} }$$
برای آشنایی بیشتر با محاسبه محیط بیضی و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «محیط بیضی — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.
فرمول های محیط و مساحت n ضلعی
n ضلعی زیر داده شده است.
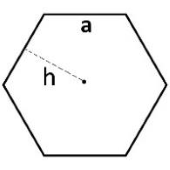
فرمول مساحت n ضلعی
مساحت یک n ضلعی با ارتفاع $$h$$ و طول ضلع $$a$$ به صورت زیر محاسبه می‌شود:
$$\large \boxed { A = \frac 12 n \times a \times h }$$
فرمول محیط n ضلعی
محیط یک n ضلعی به طول ضلع $$a$$ برابر است با:
$$\large \boxed { P = n \times a }$$
فرمول های حجم و مساحت کره
کره زیر را در نظر بگیرید.
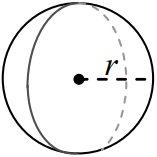
فرمول مساحت سطح کره
مساحت سطح کره‌ای به شعاع $$r$$ برابر است با:
$$\large \boxed {S = 4 \pi r ^2 }$$
مساحت سطح کره‌ای به قطر $$d$$ به صورت زیر به دست می‌آید:
$$\large \boxed {S = \pi d ^2 }$$
برای آشنایی بیشتر با محاسبه مساحت کره و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «مساحت کره و محاسبه آن | به زبان ساده» مراجعه کنید.
فرمول حجم کره
حجم کره‌ای با شعاع $$r$$ به صورت زیر محاسبه می‌شود:
$$\large \boxed { V = \dfrac { 4 } { 3 } \pi r ^ 3 } $$
برای آشنایی بیشتر با محاسبه حجم کره و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «حجم کره و محاسبه آن | به زبان ساده» مراجعه کنید.
فرمول های حجم و مساحت مکعب مستطیل
مکعب زیر را داریم.
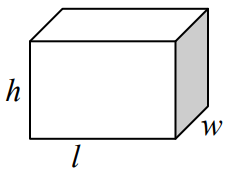
فرمول حجم مکعب مستطیل
حجم مکعب مستطیلی به ارتفاع $$h$$، طول $$ l $$ و عرض $$w $$ به صورت زیر است:
$$\large \boxed {V = h \times w \times l }$$
فرمول مساحت مکعب مستطیل
مساحت سطح مکعب مستطیلی به ارتفاع $$h$$، طول $$ l $$ و عرض $$w $$ برابر است با:
$$\large \boxed { S = 2 \times (w l + w h + l h ) }$$
برای آشنایی بیشتر با محاسبه مساحت مکعب مستطیل و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «مساحت مکعب مستطیل و محاسبه آن | به زبان ساده» مراجعه کنید.
فرمول های حجم و مساحت استوانه
استوانه زیر را داریم.
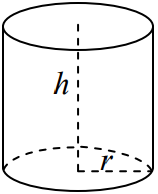
فرمول حجم استوانه
حجم استوانه‌ای با ارتفاع $$h$$ و شعاع قاعده $$r $$ برابر است با:
$$\large \boxed { V = \pi r ^ 2 h }$$
فرمول مساحت استوانه
اگر یک استوانه دارای ارتفاع $$h$$ و شعاع قاعده $$r $$ باشد، مساحت سطح آن به شکل زیر محاسبه می‌شود:
$$\large \boxed { S = 2 \pi r h }$$
برای آشنایی بیشتر با محاسبه مساحت استوانه و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «مساحت استوانه و محاسبه آن | به زبان ساده» مراجعه کنید.
فرمول های حجم و مساحت مخروط
مخروط زیر را در نظر بگیرید.
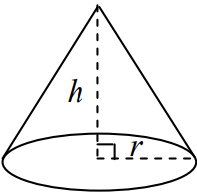
فرمول حجم مخروط
حجم مخروطی به شعاع قاعده $$r$$ و ارتفاع $$h$$، برابر است با:
$$\large \boxed { V = \dfrac { 1 } { 3 } \pi r ^ 2 h } $$
برای آشنایی بیشتر با محاسبه حجم مخروط و مثال‌های آن، پیشنهاد می‌کنیم به آموزش «حجم مخروط و محاسبه آن | به زبان ساده» مراجعه کنید.
فرمول مساحت سطح مخروط
مساحت سطح یک مخروط که شعاع قاعده آن $$r$$ و ارتفاعش $$h$$ است، به صورت زیر محاسبه می‌شود:
$$\large \boxed { S = \pi r (r + \sqrt {r ^ 2 + h ^ 2 })}$$
فرمول های حجم و مساحت مخروط ناقص
شکل زیر یک مخروط ناقص را نشان می‌دهد.
فرمول حجم مخروط ناقص
حجم یک مخروط ناقص با ارتفاع $$h$$، شعاع قاعده بالای $$r_ 2 $$ و شعاع قاعده پایین $$ r _ 1 $$ برابر است با:
$$\large \boxed { V = \frac 13 \pi h (r_1^2 + r _ 1 r_ 2 + r _ 2 ^ 2 )}$$
فرمول مساحت سطح مخروط ناقص
حجم یک مخروط ناقص با طول شیب $$s$$، شعاع قاعده بالای $$r_ 2 $$ و شعاع قاعده پایین $$ r _ 1 $$ برابر است با:
$$\large \boxed { S = \pi \times (r_ 1 + r_ 2 ) \times s }$$
فرمول های حجم و مساحت منشور
منشور زیر را داریم.
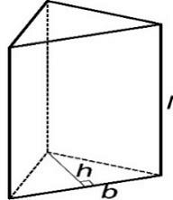
فرمول حجم منشور
حجم منشوری به طول $$l$$ و قاعده $$b$$ و ارتفاع قاعده $$h$$ برابر است با:
$$\large \boxed { V = \frac 13 l w h }$$
فرمول مساحت منشور
مساحت سطح منشوری به طول $$l$$ و قاعده $$b$$ و ارتفاع قاعده $$h$$ برابر است با:
$$\large \boxed { S = 3 b l + b h }$$
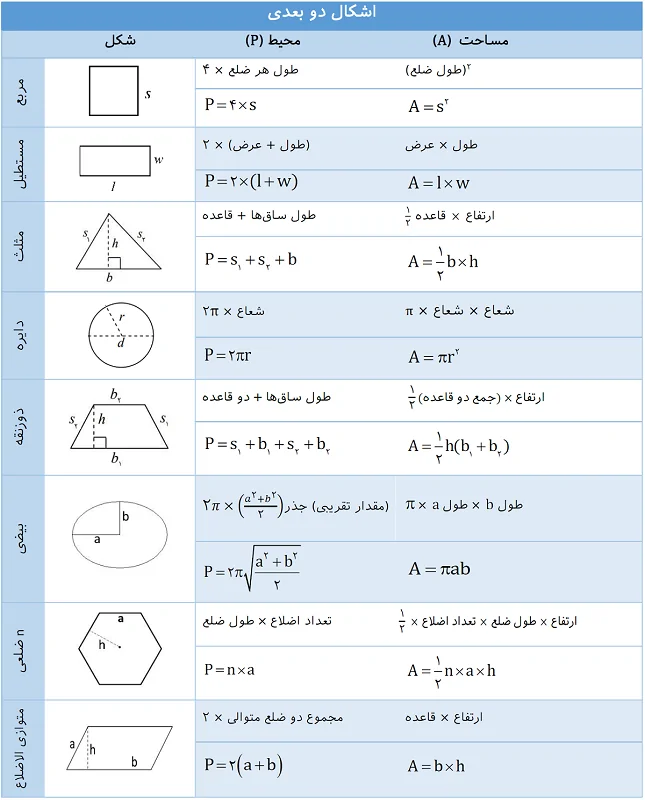
چکیده فرمول های محیط و مساحت اشکال هندسی در یک نگاه
برای دسترسی ساده‌تر به فرمول های محیط و مساحت بالا، چکیده آن‌ها را در ادامه آورده‌ایم.
چکیده فرمول های محیط و مساحت اشکال دو بعدی به صورت زیر است.
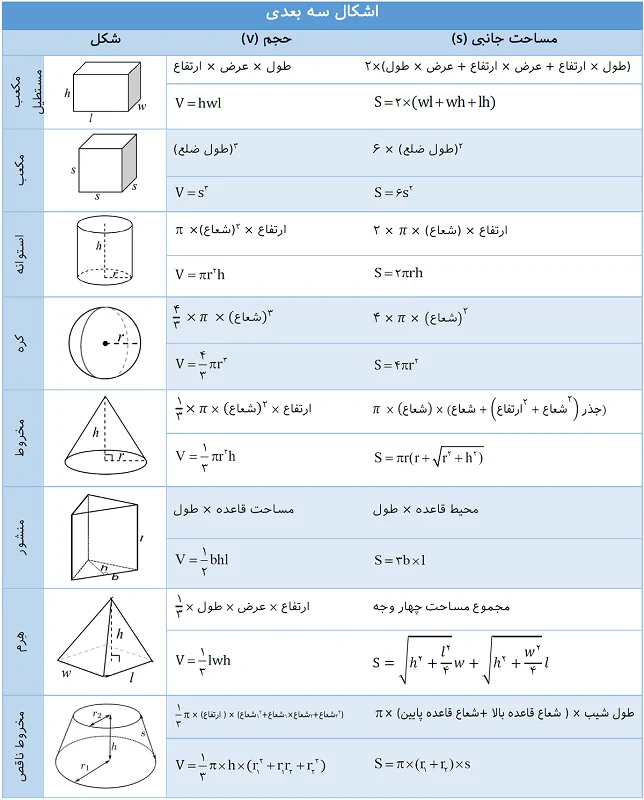
چکیده فرمول های محیط و مساحت اشکال سه بعدی در ادامه آورده شده است.
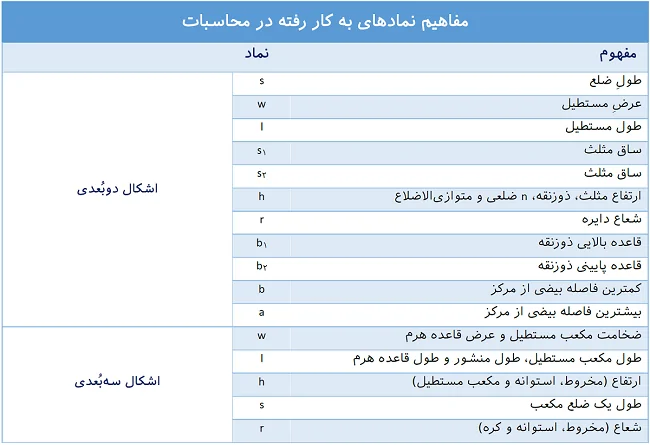
جدول زیر نیز شامل چکیده نمادهای به کار رفته در محاسبات است.
دانلود فایل pdf فرمول های محیط و مساحت و حجم
برای راحتی استفاده از فرمول های محیط و مساحت و حجم اشکال مختلف هندسی، آن‌ها را در قالب تقلب‌نامه‌های مجله فرادرس در یک فایل pdf تدوین کرده‌ایم.
این تقلب‌نامه را می‌توانید با کلیک روی لینک زیر دانلود کنید.
برای یادگیری اشکال مختلف هندسی و محاسبه محیط، مساحت و حجم آن‌ها، توصیه می‌کنیم آموزشهای مجله فرادرس را که در این زمینه تهیه شده‌اند، مطالعه کنید:
- چهار ضلعی ها در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- چندضلعی و تعریف آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- آشنایی با چند وجهی ها — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- دایره، تعریف و محاسبات آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- مثلث، تعریف و محاسبات آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- مربع و محاسبه محیط و مساحت آن — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- مستطیل و محاسبات آن — به زبان ساده (+ فیلم آموزش رایگان)
- متوازی‌الاضلاع، تعریف و محاسبات آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش رایگان)
- لوزی و محاسبات آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- کایت یا شبه‌لوزی، تعریف و محاسبات آن در هندسه — به زبان ساده
- ذوزنقه چیست؟ | محاسبات و فرمول‌ها به زبان ساده (+فیلم آموزش رایگان)
- بیضی، تعریف و محاسبات آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- مخروط، کره و استوانه — حجم و مساحت اشکال هندسی به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- مخروط و محاسبان آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- استوانه و مفاهیم آن در هندسه — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- آشنایی با منشور و محاسبات آن — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- مکعب، منشور مربعی و مکعب‌مستطیل — به زبان ساده (+ دانلود فیلم آموزش رایگان)
- مکعب در هندسه — به زبان ساده (+ دانلود فیلم آموزش رایگان)
- مساحت دایره — به زبان ساده (+ فیلم آموزش رایگان)
- مساحت مثلث — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- مساحت مستطیل — به زبان ساده (+ فیلم آموزش رایگان)
- مساحت لوزی — به زبان ساده (+ فیلم آموزش رایگان)
- محاسبه مساحت ذوزنقه — به زبان ساده
- مساحت متوازی الاضلاع و محاسبه آن | به زبان ساده
- محاسبه مساحت ذوزنقه — به زبان ساده
- مساحت کره و محاسبه آن | به زبان ساده
- مساحت مکعب مستطیل و محاسبه آن | به زبان ساده
- مساحت استوانه و محاسبه آن | به زبان ساده
- محیط دایره — به زبان ساده (+ فیلم آموزش رایگان)
- محیط مثلث — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- محیط مربع و محاسبه آن | به زبان ساده (+ فیلم آموزش رایگان)
- محیط مستطیل و محاسبه آن — به زبان ساده (+ فیلم آموزش رایگان)
- محیط لوزی — به زبان ساده (+ فیلم آموزش رایگان)
- محیط متوازی الاضلاع و محاسبه آن | به زبان ساده
- محیط ذوزنقه و محاسبه آن | به زبان ساده (+ فیلم آموزش رایگان)
- محیط بیضی — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
- حجم کره و محاسبه آن | به زبان ساده
- حجم مخروط و محاسبه آن | به زبان ساده
فیلم های آموزش فرمول های محیط و مساحت اشکال هندسی (+ فیلم و PDF رایگان)
فیلم آموزشی مساحت دایره
فیلم آموزشی محاسبه محیط دایره
فیلم آموزشی مساحت مثلث
فیلم آموزشی محیط مثلث
فیلم آموزشی محاسبه محیط مربع
فیلم آموزشی محاسبه مساحت مستطیل
فیلم آموزشی محاسبه محیط مستطیل
فیلم آموزشی مساحت لوزی
فیلم آموزشی محیط لوزی
فیلم آموزشی محیط ذوزنقه
فیلم آموزشی محیط بیضی
فیلم آموزشی مخروط
فیلم آموزشی مخروط، کره و استوانه
فیلم آموزشی حجم و مساحت رویه منشور
فیلم آموزشی استوانه و مفاهیم آن
با تشکر از زحمات این سایت و تمام دست اندر کاران.انسانیت پشت و پناهتون.به جرات میشه گفت دانشگاهی مجازی ایرانیان هستید.
سلام فرهود عزیز.
سپاس ار همراهی‌تان با مجله فرادرس.
شاد و پیروز باشید.
عالی و کامل nice.?
یعنی شماااااااا عالی هستید مطالب خیلی عالی هستن ممنون از شما.?
سلام محمدحسن عزیز.
خوشحالیم که آموزشهای مجله فرادرس برایتان مفید بوده‌اند.
شاد و پیروز باشید.
به من خیلی کمک کرد.
ازتون ممنونم.
سلام.
خوشحالیم که آموزشهای مجله فرادرس برایتان مفید بوده است.
سپاس از همراهی‌تان.
خیلی عالی بود
عالی بود
بسیارعالی دست شمادر نکند.