محیط مستطیل چگونه بدست می آید؟ + فیلم آموزشی و حل تمرین و مثال

محیط مستطیل برابر «حاصل جمع طول و عرض ضرب‌در دو» است. البته امکان محاسبه محیط این چهار ضلعی توسط اندازه قطر و یکی از ضلع‌های آن نیز وجود دارد. محیط شکل‌های هندسی اصلی مانند مستطیل، از اهمیت بالایی در زندگی روزمره برخوردار هستند. در این مقاله، نحوه محاسبه محیط مستطیل را با استفاده از روش‌های مختلف و مثال‌های کاربردی متنوع آموزش می‌دهیم.

مستطیل چیست؟

مستطیل (به انگلیسی Rectangle)، یک شکل چند ضلعی است که از چهار ضلع و چهار راس با زاویه 90 درجه تشکیل می‌شود. تصویر زیر، نمونه‌ای از یک مستطیل را نمایش می‌دهد. این شکل چهار ضلعی، شباهت زیادی به مربع دارد. با این تفاوت که در مستطیل، طول تمام ضلع‌ها برابر نبوده و ضلع‌های رو به رویی با هم برابر هستند. ضلع‌های بزرگ‌تر مستطیل، با عنوان «طول» و ضلع‌های کوچک‌تر آن، با عنوان «عرض» شناخته می‌شوند.

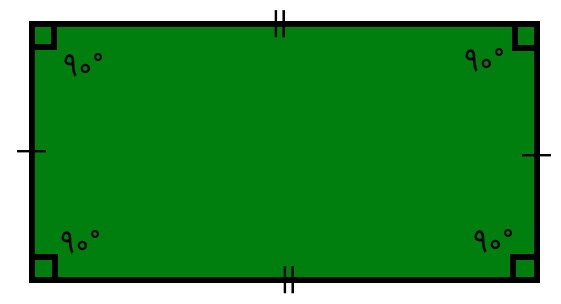
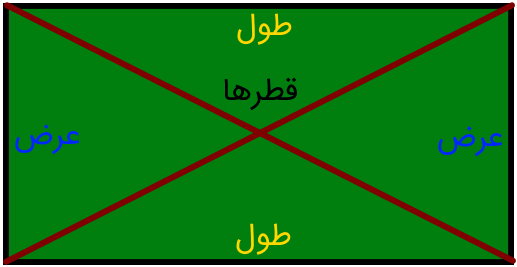
به پاره خط اتصال دهنده دو راس رو به رویی مستطیل، قطر مستطیل می‌گویند. اندازه طول، عرض و قطر، از مقادیر مورد استفاده در محاسبه محیط و مساحت مستطیل هستند.

محیط چیست؟

محیط (به انگلیسی Perimeter)، مجموع طول ضلع‌های تشکیل دهنده یک شکل هندسی بسته است. از شناخته شده‌ترین شکل‌های منتظم بسته می‌توان به مربع، مستطیل، لوزی، دایره، متوازی الاضلاع و مثلث اشاره کرد.

محیط مستطیل چیست ؟

محیط مستطیل، اندازه دور آن یا مجموع طول ضلع‌های تشکیل دهنده این شکل هندسی است. برای درک مفهوم محیط، یک مستطیل با طول و عرض دلخواه را بر روی کاغذ رسم کنید.

سپس قلم خود را بر روی یک نقطه از ضلع‌های آن قرار داده و در مسیر ساعت‌گرد یا پادساعتگرد حرکت دهید. با بازگشت قلم به نقطه شروع، حرکت آن را متوقف کنید. طول مسیر طی شده توسط قلم، همان محیط مستطیل است.

مطابق با مسیر مشخص شده در تصویر بالا، رابطه محیط مستطیل به صورت زیر نوشته می‌شود:

جمع تمام ضلع‌ها = محیط

عرض + طول + عرض + طول = محیط مستطیل

(عرض) $$\times$$ 2 + (طول) $$\times$$ 2 = محیط مستطیل

(طول + عرض) $$\times$$ 2 = محیط مستطیل

محیط مستطیل چگونه بدست می آید ؟

محیط مستطیل، از جمع طول و عرض مستطیل ضرب در 2 به دست می‌آید. البته در صورت دانستن مقدار قطر و یکی از ضلع‌ها (طول یا عرض)، امکان محاسبه محیط وجود خواهد داشت. در بخش‌‌های بعدی به نحوه استفاده از قطر و فرمول مربوط به آن خواهیم پرداخت.

مثال: محاسبه محیط در

درهای ساختمان، معمولا به شکل مستطیل ساخته می‌شوند. تصویر زیر، درِ یکی از اتاق‌های ساختمان را نمایش می‌دهد. اگر طول داخلی چارچوب در، برابر 210 سانتی‌متر و عرض داخلی آن برابر 80 سانتی‌متر باشد، محیط درِ نصب شده درون آن چقدر است؟

محیط در با محیط داخل چارچوب برابر است. به منظور محاسبه این محیط، ابتدا رابطه محیط مستطیل را می‌نویسیم:

(طول + عرض) $$\times$$ 2 = محیط مستطیل

سپس، رابطه بالا را بر حسب مقادیر چارچوب بازنویسی می‌کنیم:

(طول چارچوب + عرض چارچوب) $$\times$$ 2 = محیط چارچوب

(210 + 80) $$\times$$ 2 = محیط چارچوب

(290) $$\times$$ 2 = محیط چارچوب

580 = محیط چارچوب

در نتیجه، محیط درِ نصب شده درون چارچوب برابر 580 سانتی‌متر است.

علامت ریاضی محیط چیست؟

در ریاضیات، محیط مستطیل و دیگر شکل‌های هندسی با حرف انگلیسی P نمایش داده می‌شود. این حرف، ابتدای کلمه «Perimeter» به معنای «محیط» است. حرف انگلیسی l به منظور نمایش طول، حرف انگلیسی w، برای عرض و حرف انگلیسی d جهت نشان دادن قطر مستطیل مورد استفاده قرار می‌گیرد.

فرمول محیط مستطیل چیست؟

برای نوشتن فرمول محیط مستطیل به صورت عبارت جبری، از علامت‌های ریاضی استفاده می‌کنیم. بر این اساس، فرمول محاسبه محیط مستطیل با طول و عرض به شکل زیر است:

$$P = 2 \times ( l + w )$$

• P: محیط
• l: طول مستطیل
• w: عرض مستطیل

فرمول محیط مستطیل، با استفاده از اندازه قطر و یکی از اضلاع نیز نوشته می‌شود. در بخش آخر این آموزش، به معرفی این فرمول و تشریح مثال‌های مربوط به آن خواهیم پرداخت.

کاربرد محیط مستطیل چیست؟

محیط اطراف ما از اجسامی با شکل‌های متنوع تشکیل شده است. مستطیل، یکی از شکل‌های پرکاربرد برای ساخت وسایل و سازه‌های مختلف به شمار می‌رود. تجهیزات الکترونیکی، زمین ساختمان‌ها، لوازم خانگی، زمین‌های ورزشی و غیره، معمولا به شکل مستطیل ساخته می‌شوند. به همین دلیل، یادگیری نحوه محاسبه محیط مستطیل، از اهمیت بالایی در طراحی و مهندسی این اجسام برخوردار است.

حل مثال های کاربردی محیط مستطیل

در این بخش، شش مثال متنوع را در زمینه محاسبه محیط مستطیل در حالت‌های مختلف حل می‌کنیم.

مثال اول: تعیین محیط با طول و عرض

مستطیلی دارای طول 7 و عرض 6 است. محیط مستطیل را به دو صورت (مطابق با تعریف و مطابق با فرمول) به دست آورید.

به منظور درک بهتر مسئله، ابتدا شکل مستطیل را رسم کرده و اندازه‌های داده شده را بر روی ضلع‌های مستطیل یادداشت می‌کنیم.

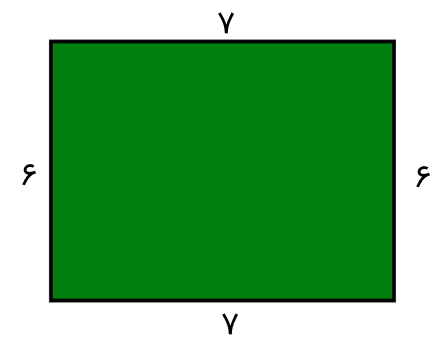
مطابق با تعریف، اندازه دور هر شکل را محیط آن شکل می‌گویند. در نتیجه محیط مستطیل بالا برابر است با:

عرض + طول + عرض + طول = محیط مستطیل

6 + 7 + 6 + 7 = محیط مستطیل

26 = محیط مستطیل

مطابق با فرمول محیط مستطیل، داریم:

(عرض) $$\times$$ 2 + (طول) $$\times$$ 2 = محیط مستطیل

(6) $$\times$$ 2 + (7) $$\times$$ 2 = محیط مستطیل

12 + 14 = محیط مستطیل

26 = محیط مستطیل

به این ترتیب، محیط مستطیلی به طول 7 و عرض 6 برابر 26 است.

مثال دوم: تعیین مسافت پیاده روی

شخصی هر روز، اطراف یک زمین ورزشی به پیاده‌روی می‌پردازد. این زمین، به شکل مستطیل بوده و اندازه ضلع‌های آن برابر با 90 و 40 متر است.

با توجه به اطلاعات تصویر بالا، به سوالات زیر پاسخ دهید؟

1. این شخص، با یک دور پیاده‌روی کامل در اطراف این زمین، فرد چه مسافتی را طی خواهد کرد؟
2. اگر این شخص، پنج دور اطراف این زمین پیاده‌وری کند، مجموع مسافت طی شده چقدر خواهد بود؟
3. اگر این شخص بخواهد هر روز به اندازه 3900 متر پیاده‌روی کند، باید چند دور کامل اطراف زمین بزند؟

برای جواب دادن به سوالات بالا، ابتدا شکل ساده شده مسئله را رسم می‌کنیم.

جواب سوال 1

اگر شخص، یک دور کامل در اطراف زمین پیاده‌روی کند، مسافت پیاده‌روی او برابر با محیط زمین خواهد بود. محیط این زمین برابر است با:

$$P = 2 \times ( l + w )$$

(طول + عرض) $$\times$$ 2 = محیط مستطیل

(طول زمین + عرض زمین) $$\times$$ 2 = محیط زمین

(90 + 40) $$\times$$ 2 = محیط زمین

(130) $$\times$$ 2 = محیط زمین

260 = محیط زمین

محیط زمین ورزشی برابر 260 متر است. بنابراین، مسافت یک دور کامل پیاده‌روی در اطراف این زمین برابر 260 متر خواهد بود.

جواب سوال 2

اگر شخص، پنج دور در اطراف زمین پیاوری کند، مسافت طی شده توسط او، از رابطه زیر محاسبه می‌شود:

محیط زمین $$\times$$ تعداد دور = مسافت پیاده‌روی

260 $$\times$$ 5 = مسافت پیاده‌روی

1300 = مسافت پیاده‌روی

مسافت پنج دور زمین ورزشی برابر 1300 متر است.

جواب سوال 3

برای تعیین تعداد دورهای مورد نیاز برای طی کردن 3900 متر پیاده‌روی در اطراف زمین ورزشی، باید مسافت مورد نظر خود را بر محیط زمین تقسیم کرد:

محیط زمین $$\times$$ تعداد دور = مسافت پیاده‌روی

تعداد دور = محیط زمین ÷ مسافت پیاده‌روی

تعداد دور = 260 ÷ 3900

تعداد دور = 15

شخص، با 15 دور پیاده‌روی در اطراف زمین ورزشی، می‌تواند مسافت 3900 متر را طی کند.

مثال سوم: محاسبه مجموع محیط‌ها

در تصویر زیر، سه مستطیل با طول و عرض متفاوت نمایش داده شده است. مجموع محیط‌های این مستطیل‌ها چقدر است؟

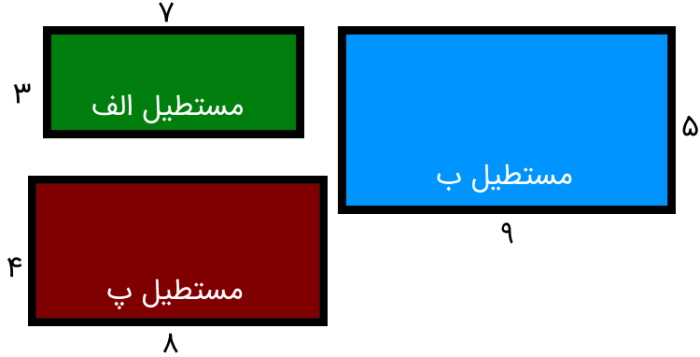
مطابق با تصویر بالا، اندازه‌های داده شده را یادداشت می‌کنیم:

• مستطیل الف
  • طول: 7 متر
  • عرض: 3 متر
• مستطیل ب
  • طول: 9 متر
  • عرض: 5 متر
• مستطیل پ
  • طول: 8 متر
  • عرض: 4 متر

محاسبه محیط‌ها را از یکی از مستطیل‌ها، مانند الف شروع می‌کنیم:

(طول الف + عرض الف) $$\times$$ 2 = محیط الف

(3 + 7) $$\times$$ 2 = محیط الف

(10) $$\times$$ 2 = محیط الف

20 = محیط الف

محیط مستطیل ب برابر است با:

(طول ب + عرض ب) $$\times$$ 2 = محیط ب

(9 + 5) $$\times$$ 2 = محیط ب

(14) $$\times$$ 2 = محیط ب

28 = محیط ب

محیط مستطیل پ نیز به صورت زیر تعیین می‌شود:

(طول پ + عرض پ) $$\times$$ 2 = محیط پ

(8 + 4) $$\times$$ 2 = محیط پ

(12) $$\times$$ 2 = محیط پ

24 = محیط پ

مجموع محیط‌های این سه مستطیل از رابطه زیر به دست می‌آید:

محیط پ + محیط ب + محیط الف = جمع محیط‌ها

24 + 28 + 20 = جمع محیط‌ها

72 = جمع محیط‌ها

مجموع محیط‌های سه مستطیل برابر 72 متر است.

مثال چهارم: پیدا کردن اندازه ضلع از روی محیط

اگر مجموع محیط‌های دو مستطیل نمایش داده شده در تصویر زیر برابر 68 سانتی‌متر باشد، عرض مستطیل کوچک‌تر چقدر است؟

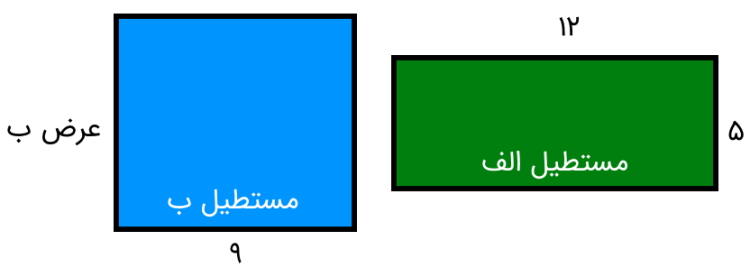
پیش از شروع انجام محاسبات، اطلاعات داده شده را یادداشت می‌کنیم:

• مستطیل الف
  • طول: 12
  • عرض: 5
• مستطیل ب
  • طول: 9
  • عرض: ؟

به دلیل مشخص بودن طول و عرض مستطیل الف، می‌توانیم محیط آن را به صورت زیر محاسبه کنیم:

(طول الف + عرض الف) $$\times$$ 2 = محیط الف

(12 + 5) $$\times$$ 2 = محیط الف

(17) $$\times$$ 2 = محیط الف

34 = محیط الف

مجموع محیط‌های دو مستطیل برابر است با:

محیط ب + محیط الف = مجموع محیط‌ها

محیط ب + 34 = 68

محیط ب = 34 - 68

محیط ب = 34

محیط مستطیل کوچک برابر 34 سانتی‌متر است. به دلیل مشخص بودن مقدار طول مستطیل کوچک و به دست آوردن محیط آن، امکان تعیین عرض این مستطیل از رابطه زیر فراهم می‌شود:

(طول ب + عرض ب) $$\times$$ 2 = محیط ب

(9 + عرض ب) $$\times$$ 2 = 34

۹ $$\times$$ 2 + عرض ب $$\times$$2 = 34

18 + عرض ب $$\times$$2 = 34

عرض ب $$\times$$2 = 18 - 34

عرض ب $$\times$$2 = 16

عرض ب = 2 ÷ 16

عرض ب = 8

در نتیجه عرض مستطیل ب برابر 8 سانتی‌متر است. نکته جالب در مورد این دو مستطیل این است که با وجود برابر بودن محیط‌ها آن‌ها (34 سانتی‌متر)، مساحت مستطیل ب بزرگ‌تر است. برای یادگیری در زمینه مقایسه مساحت‌های مستطیل، مطالعه مطلب «آموزش مساحت مستطیل به زبان ساده» را به شما پیشنهاد می‌کنیم.

مثال پنجم: پیدا کردن شکل با بزرگ‌ترین محیط

از بین شکل‌های نمایش داده شده در تصویر زیر، محیط کدام بیشتر است؟

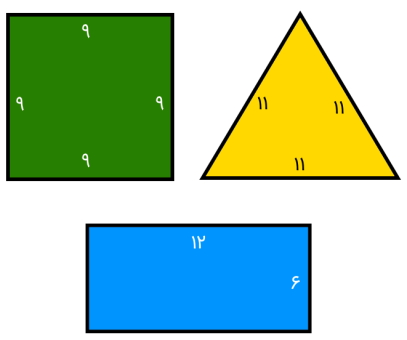
پیش از شروع محاسبات، اطلاعات مسئله را یادداشت می‌کنیم:

• مستطیل
  • طول: 12
  • عرض: 5
• مربع
  • ضلع: 9
• مثلث متساوی الاضلاع
  • ضلع: 11

رابطه محاسبه محیط مستطیل برابر است با:

(طول + عرض) $$\times$$ 2 = محیط مستطیل

(12 + 5) $$\times$$ 2 = محیط مستطیل

(17) $$\times$$ 2 = محیط مستطیل

34 = محیط مستطیل

با توجه به تعریف، محیط، جمع ضلع‌های تشکیل‌دهنده یک شکل هندسی است. به دلیل برابر بودن هر چهار ضلع مربع، محیط آن به صورت زیر محاسبه می‌شود:

ضلع + ضلع + ضلع + ضلع = محیط مربع

9 + 9 + 9 + 9 = محیط مربع

36 = محیط مربع

هر سه ضلع مثلث متساوی الاضلاع نیز با هم برابر هستند. به همین دلیل، محیط این شکل، از رابطه زیر به دست می‌آید:

ضلع + ضلع + ضلع = محیط مثلث متساوی الاضلاع

11 + 11 + 11 = محیط مثلث متساوی الاضلاع

33 = محیط مثلث متساوی الاضلاع

در نتیجه، از میان شکل‌های بالا، محیط مربع بیشتر است. برای یادگیری فرمول‌های محاسبه مستقیم محیط مربع و مثلث، مطالب «آموزش محاسبه محیط مربع به زبان ساده» و «آموزش محیط مثلث به زبان ساده» را به شما پیشنهاد می‌کنیم.

مثال ششم: محاسبه محیط از روی مساحت و طول یک ضلع

محیط مستطیلی با مساحت 120 متر مربع و عرض ۸ متر چقدر است؟

محیط مستطیل با استفاده از اندازه طول و عرض آن به دست می‌آید. به دلیل مشخص نبودن طول در صورت سوال، ابتدا این اندازه را تعیین می‌کنیم. برای حل این مسئله باید با نحوه محاسبه مساحت مستطیل آشنا باشید. فرمول محاسبه مساحت مستطیل عبارت است از:

عرض $$\times$$ طول = مساحت مستطیل

اندازه‌های داده شده در صورت سوال را در رابطه بالا قرار می‌دهیم:

8 $$\times$$ طول = 120

طول = 8 ÷ 120

طول = 15

اکنون اندازه‌های طول و عرض مستطیل مشخص هستند. با استفاده از این اندازه‌ها و رابطه زیر، محیط مستطیل را به دست می‌آوریم:

(طول + عرض) $$\times$$ 2 = محیط مستطیل

(15 + 8) $$\times$$ 2 = محیط مستطیل

(23) $$\times$$ 2 = محیط مستطیل

46 = محیط مستطیل

محیط مستطیل برابر با 46 متر است.

محاسبه محیط مستطیل با قطر و یک ضلع

یکی دیگر از روش‌های محاسبه مستطیل، استفاده از اندازه قطر و یکی از ضلع‌های آن است. محاسبه محیط مستطیل با این روش، توسط مفاهیمی نظیر توان، جذر و قضیه فیثاغورس انجام می‌گیرد. تصویر زیر، یک مستطیل را به همراه یکی از قطرها و علامت جبری ضلع‌های آن را نمایش می‌دهد.

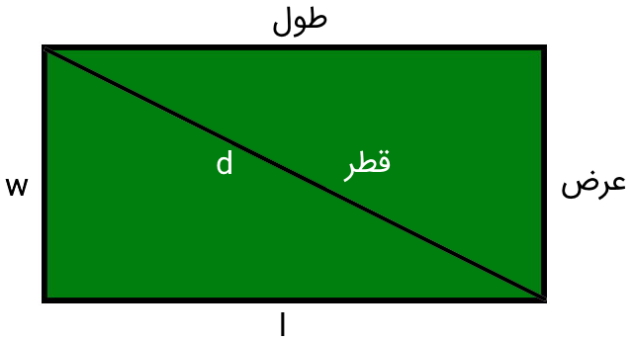
در صورت مشخص بودن قطر و طول مستطیل، فرمول جبری محاسبه محیط مستطیل با قطر به صورت زیر نوشته می‌شود:

$$P=2 l+2 \sqrt{d^{2}-l^{2}}$$

• P: محیط
• l: طول مستطیل
• d: قطر مستطیل

اگر قطر و عرض مستطیل مشخص باشد، می‌توان فرمول بالا را به صورت زیر نوشت:

$$P=2 w+2 \sqrt{d^{2}-w^{2}}$$

• P: محیط
• w: عرض مستطیل
• d: قطر مستطیل

مثال: محاسبه محیط توسط قطر و عرض

محیط و طول مستطیلی با قطر 5 و عرض 3 چقدر است؟

پیش از حل مسئله، اطلاعات داده شده را یادداشت می‌کنیم:

• عرض مستطیل: 3
• قطر مستطیل: 5
• محیط مستطیل: ؟
• طول مستطیل: ؟

مطابق با فرمول محیط مستطیل بر اساس قطر، داریم:

$$P=2 w+2 \sqrt{d^{2}-w^{2}}$$

مقادیر قطر و عرض را در فرمول بالا قرار می‌دهیم:

$$P=(2 \times 3)+ (2 \sqrt{5^{2}-3^{2}})$$

$$P=(6)+ (2 \sqrt{25-9})$$

$$P=(6)+ (2 \sqrt{16})$$

$$P=(6)+ (2 \times 4)$$

$$P=(6)+ (8)$$

$$P=14$$

محیط مستطیل برابر 14 است. برای تعیین طول مستطیل، فرمول محیط بر اساس طول و عرض را می‌نویسیم:

$$P = 2 \times ( l + w )$$

اندازه عرض را از صورت سوال و مقدار محیط را از مرحله قبل درون فرمول بالا قرار می‌‌دهیم:

$$14 = 2 \times ( l + 3 )$$

$$14 = ( 2 \times l ) + ( 2 \times 3 )$$

$$14 = ( 2 \times l ) + ( 6 )$$

$$14 - 6= 2 \times l$$

$$8 = 2 \times l$$

$$8 ÷ 2 = l$$

$$4 = l$$

در نتیجه، طول مستطیلی با قطر 5 و عرض 3 برابر 4 است.