مخروط چیست؟ | تعریف، شکل، مفاهیم و فرمول ها

در آموزش‌های قبلی مجله فرادرس، مطالبی را درباره برخی از اشکال هندسی سه‌بعدی از قبیل استوانه بیان کردیم. در این آموزش، با مخروط آشنا می‌شویم، انواع آن را معرفی و روش محاسبه حجم و مساحت سطح آن را بیان می‌کنیم.

مخروط چیست؟

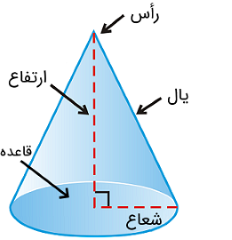
مخروط یک شکل سه‌بعدی در هندسه است که از یک قاعده دایره‌ای صاف شروع شده و به آرامی به یک نقطه می‌رسد که یک محور را به مرکز قاعده می‌سازد. این نقطه رأس نام دارد. همچنین، می‌توانیم مخروط‌ را به عنوان هرمی تعریف کنیم که دارای یک سطح مقطع دایره‌ای است. این مخروط‌ها به عنوان مخروط‌ دایره‌ای نیز شناخته می‌شوند.

طبق یک تعریف دقیق‌تر، مخروط شکلی است که با مجموعه‌ای از پاره‌خط‌هایی تشکیل می‌شود که یک نقطه مشترک به نام رأس را به تمام نقاط مرز یک قاعده دایره‌ای متصل می‌کنند. فاصله از رأس و طول مخروط‌ از رأس تا هر نقطه از محیط قاعده «یال» نامیده می‌شود.

شکل زیر رأس، ارتفاع، یال، قاعده و شعاع قاعده مخروط‌ را نشان می‌دهد.

نکته: احتمالاً شنیده‌اید که به برخی اجسام مخروطی می‌گویند. در واقع، به هر جسمی که شبیه یک مخروط‌ باشد، «مخروط» گفته می‌شود.

شکل زیر چند نمونه مخروط‌ را نشان می‌دهد که در زندگی روزمره در اطراف خود می‌بینیم.

برای آشنایی بیشتر با مباحت هندسه و ریاضیات، پیشنهاد می‌کنیم به مجموعه فیلم‌های آموزش دروس دبیرستان و پیش دانشگاهی فرادرس مراجعه کنید که لینک آن در ادامه آورده شده است.

• برای مشاهده مجموعه فیلم‌های آموزش دروس دبیرستان و پیش دانشگاهی + اینجا کلیک کنید.

انواع مخروط

مخروط‌ها را می‌توان به سه دسته قائم، مایل و ناقص تقسیم کرد.

مخروط قائم

مخروط قائم نوعی مخروط‌ است که در آن، فاصله همه نقاط روی دایره قاعده از رأس مخروط یکسان باشد. به عبارت دیگر، اگر خطی عمود از مرکز قاعده دایره‌ای رسم کنیم، از رأس مخروط عبور خواهد کرد. شکل زیر یک مخروط قائم را نشان می‌دهد.

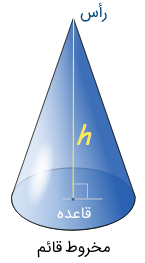
مخروط مایل

مخروط مایل نوعی مخروط است که اصطلاحاً کج شده است. در واقع، در مخروط مایل، اگر خط عمود بر قاعده از رأس (یا همان ارتفاع) برا خطی که از رأس و مرکز دایره قاعده می‌گذرد، منطبق نیست. شکل زیر یک مخروط مایل را نشان می‌دهد.

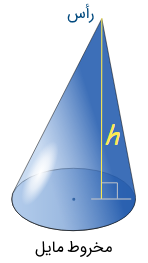
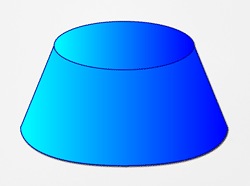
مخروط ناقص

مخروط ناقص اصطلاحاً به مخروطی می‌گویند که از بالا بریده شده باشد. شکل زیر یک مخروط ناقص را نشان می‌دهد.

مساحت سطح مخروط

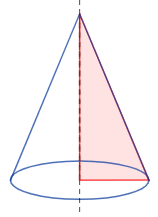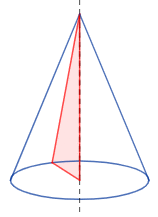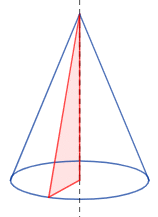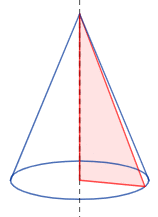
مساحت مخروط‌ برابر با مجموع مساحت سطح جانبی مخروط‌ و مساحت قاعده آن است. قاعده یک دایره است و سطح جانبی بخشی از یک دایره به شعاع یال مخروط. شکل زیر مساحت سطح جانبی مخروط‌ را به خوبی نشان می‌دهد.

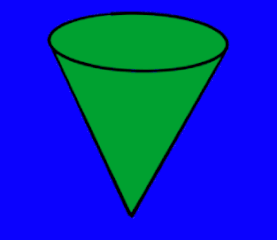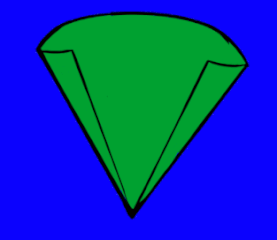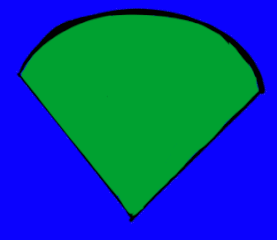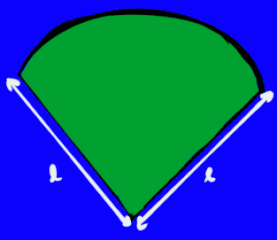
بنابراین، مساحت کل سطح مخروط به صورت شکل زیر خواهد بود.

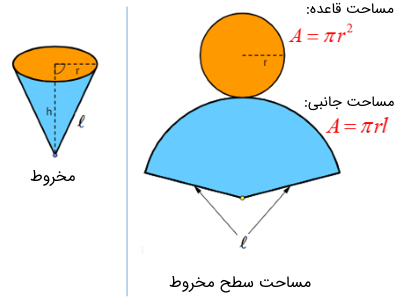
بنابراین، مساحت مخروطی با اندازه یال $$l$$ و شعاع قاعده $$r$$، برابر خواهد بود با:

$$ \large A  =\pi r ^ 2 + \pi r  l= \pi r (r + l)=\pi \times 3 \times (3+5) = 24 \pi $$

نکته: اگر اندازه ارتفاع $$h$$ را داشته باشیم، می‌توانیم مقدار $$l$$ را با استفاده از قضیه فیثاغورس محاسبه کنیم:

$$ \large l = \sqrt {r^2+h^2}$$

حجم مخروط

فرمول محاسبه حجم مخروط‌ را می‌توان برای سه مخروطی که در بالا به آن‌ها اشاره کردیم، بیان کرد.

حجم مخروط قائم

برای محاسبه حجم مخروط‌ قائم کافی است شعاع قاعده و ارتفاع آن را داشته باشیم. شکل زیر یک مخروط‌ قائم را با شعاع قاعده $$r$$ و ارتفاع $$h$$ نشان می‌دهد.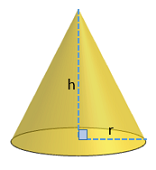

فرمول محاسبه حجم مخروط‌ به صورت زیر است:

$$ \large \boxed { V = \dfrac { 1 } { 3 } \pi r ^ 2 h } $$

نکته: شاید برایتان جالب باشد که بدانید حجم استوانه‌ای با شعاع قاعده و ارتفاع مشخص، سه برابر مخروطی با همان شعاع قاعده و ارتفاع است. تصویر متحرک زیر این موضوع را به خوبی نشان می‌دهد.

حجم مخروط مایل

شکل زیر یک مخروط‌ مایل را نشان می‌دهد.

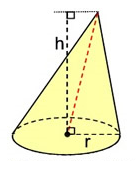
حجم یک مخروط‌ مایل با ارتفاع $$ h$$ و شعاع قاعده $$r$$ با فرمول زیر به دست می‌آید و تفاوتی با مخروط‌ قائم ندارد:

$$ \large V = \dfrac { 1 } { 3 } \pi r ^ 2 h $$

فرمول حجم مخروط ناقص

همان‌طور که در بالا گفتیم، مخروط‌ ناقص اصطلاحاً به مخروطی می‌گویند که از بالا بریده شده باشد. شکل زیر یک مخروط ناقص را نشان می‌دهد.

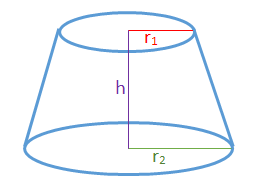
حجم یک مخروط ناقص با شعاع قاعده کوچک $$r_1$$ و شعاع قاعده بزرگ $$r_2$$ و ارتفاع $$h$$ با فرمول زیر به دست می‌آید:

$$ \large V = \frac 13 \times \pi \times h \times (r_1^2 +r_1r_2+r_2^2) $$

مثال های مخروط

در این بخش، چند مثال را درباره مخروط حل می‌کنیم.

مثال اول مخروط

اندازه یال مخروطی $$25$$ و شعاع قاعده‌اش برابر با $$24$$ است. حجم آن را به دست آورید.

حل: $$h$$ و $$l$$ را به ترتیب به عنوان ارتفاع و یال مخروط فرض می‌کنیم. برای محاسبه حجم مخروط باید شعاع قاعده $$r$$ و ارتفاع $$h$$ را بیابیم. ارتفاع را با استفاده از یال و قضیه فیثاغورس محاسبه می‌کنیم:

$$ \large \begin {aligned} l & =\sqrt { h ^ 2 + r ^ 2 } \\ 2 5 ^ 2 & = \sqrt { h ^ 2 + 2 4 ^ 2 } \\ h ^ 2 & = 4 9 \\ h & = 7 . \end {aligned} $$

بنابراین، حجم مخروط برابر خواهد بود با:

$$ \large \frac { 1 } { 3 } \pi \times 2 4 ^ 2 \times 7 = 1 3 4 4 \pi . $$

مثال دوم مخروط

ساعت شنی زیر داده شده است. پیش از خالی شدن شنِ‌ مخروط بالایی در مخروط پایینی، شخصی باید به سؤال‌هایی که مطرح می‌شود پاسخ دهد. سرعت ریزش شن $$50$$ میلی‌متر مکعب بر ثانیه است. مدت زمان پاسخ به سؤالات را بر حسب ثانیه به دست آورید.

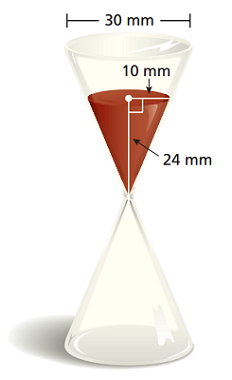
حل: ابتدا حجم شن در مخروط بالایی را به دست می‌آوریم:

$$ \large V = \dfrac { 1 } { 3 } \pi r ^ 2 h = \dfrac { 1 }{ 3 } \pi \cdot 1 0 ^ 2 \cdot 2 4 = 8 0 0 \pi . $$

بنابراین، حجم شن موجود در مخروط $$800 \pi$$ میلی‌متر مکعب است. برای یافتن زمانی که باید به سؤال پاسخ داده شود، باید حجم را بر سرعت ریزش تقسیم کنیم:

$$ \large 800 \pi\times\dfrac{1}{50}=16\pi\approx 50.265\text{ (seconds)}. $$

مثال سوم مخروط

مخروط زیر داده شده است که در آن، $$h=4$$ و $$r=3$$. مساحت سطح این مخروط را محاسبه کنید.

حل: ابتدا طول یال $$l$$ را با استفاده از قضیه فیثاغورس محاسبه می‌کنیم:

$$ \large l  = \sqrt { h ^ 2 + r ^ 2 } = \sqrt {4 ^ 2 + 3 ^ 2 } = \sqrt {25} = 5 $$

بنابراین، $$l=5$$ و $$r=3$$ را داریم. با توجه به فرمولی که بیان کردیم، مساحت مخروط به صورت زیر به دست می‌آید:

$$ \large A  =\pi r ^ 2 + \pi r  l= \pi r (r + l)=\pi \times 3 \times (3+5) = 24 \pi $$

معرفی فیلم آموزش هندسه پایه دهم (هندسه ۱) فرادرس 

برای آشنایی بیشتر با مباحث اشکال هندسی، پیشنهاد می‌کنیم به فیلم آموزش هندسه پایه دهم (هندسه ۱) مراجعه کنید که توسط فرادرس تهیه شده است. این آموزش ویدیویی که مدت زمان آن ۴ ساعت و ۳ دقیقه است، شامل چهار درس می‌شود.

در درس اول این آموزش، موضوعات ترسیم‌های هندسی و استدلال بیان شده‌اند. مباحث درس دوم، به قضیه تالس و تشابه مثلث‌ها و کاربردهای آن‌ها اختصاص یافته است. در درس سوم، مباحث مربوط به چندضلعی‌ها و ویژگی‌هایی از آن‌ها و همچنین، مساحت و کاربردهای آن مورد بیان شده است. در نهایت، موضوع درس چهارم، تجسم فضایی است که خط، نقطه و صفحه و همچنین تفکر تجسمی را شامل می‌شود.

• برای مشاهده فیلم آموزش هندسه پایه دهم (هندسه ۱) + اینجا کلیک کنید.

برای یادگیری اشکال مختلف هندسی و محاسبه محیط، مساحت و حجم آن‌ها، توصیه می‌کنیم آموزش‌های مجله فرادرس را که در این زمینه تهیه شده‌اند، مطالعه کنید: