فشار استاتیک چیست؟ – توضیح به زبان ساده
یکی از مهمترین مفاهیمی که اثر آن را در موقعیتهای مختلفی مانند شنا کردن، نوشیدن به کمک نی و ... حس میکنیم، کمیتی به نام «فشار» (Pressure) است. در مطالعه فشار، با کمیتها و اصطلاحات مختلفی روبرو میشویم که یکی از آنها «فشار استاتیک» (Static Pressure) است. فشار استاتیک، همان فشار ترمودینامیکی یک سیال ساکن است، یعنی فشاری که ناشی از سرعتهای موضعی سیال نیست. به این فشار، «فشار هیدروستاتیک» (Hydrostatic Pressure) هم گفته میشود. در این مطلب از مجله فرادرس میخواهیم توضیح دهیم که فشار استاتیک چیست، چگونه بهدست میآید و چه تفاوتهایی با انوع دیگر فشار دارد.
- یاد خواهید گرفت فشار استاتیک را از فشار دینامیک و فشار کل تفکیک کنید.
- خواهید آموخت چگونه فشار کل را بهعنوان جمع فشارهای استاتیک و دینامیک محاسبه کنید.
- میآموزید معادله برنولی و اصل پاسکال را در تحلیل جریان سیال به کار ببرید.
- یاد میگیرید از ابزارهای مختلف مثل پیزومتر و لوله پیتوت برای اندازهگیری فشار استفاده کنید.
- توانایی تبدیل و مقایسه واحدهای مختلف فشار مانند پاسکال و atm را پیدا میکنید.
- میآموزید مفهوم فشار مطلق و گیج را در کاربردهای عملی تشخیص دهید.


فشار استاتیک چیست؟
فشار استاتیک یک جریان آزاد، فشاری است که در صورت حذف تمام نیروهای وارد بر سیال، حاصل میشود. پس این فشار، فشار سیالی است که حرکتی ندارد و توسط نیروی وزن آن تولید میشود. طبق اصل برنولی، همواره مجموع تمام انرژیهای یک سیال، شامل انرژی جنبشی و پتانسیل آن باید ثابت بماند. اگر مجموع انرژیهای یک سیال آزاد در نقطه شروع حرکت را «فشار کل» (Total Pressure) در نظر بگیریم، فشار استاتیک بیانگر انرژی پتانسیل سیال و «فشار دینامیک» (Dynamic Pressure) بیانگر انرژی جنبشی یک سیال است. برای یک مایع، فشار استاتیک همان فشار ترمودینامیکی مایع به شکل است.
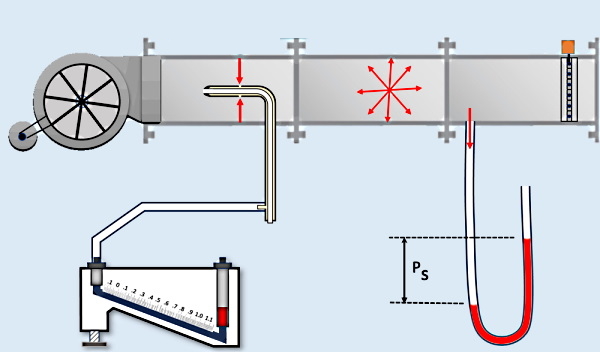
شکل زیر مفهوم فشار استاتیک را بهخوبی توضیح میدهد. در قسمت بالای این شکل، لوله افقی حاوی سیالی است که جریان ندارد یا ساکن است. اگر دقت کنید درب انتهای این لوله در سمت چپ بسته است. مشاهده میکنید که برای سیال ساکن، فشار دینامیک (پیکانهای آبی) که وابسته به سرعت سیال است، وجود ندارد. بنابراین تنها فشاری که در این لوله به دیوارههای آن وارد میشود، فشار استاتیک (پیکانهای قرمز) یا Ps است. برای این لوله فشار کل برابر میشود با فشار استاتیک.
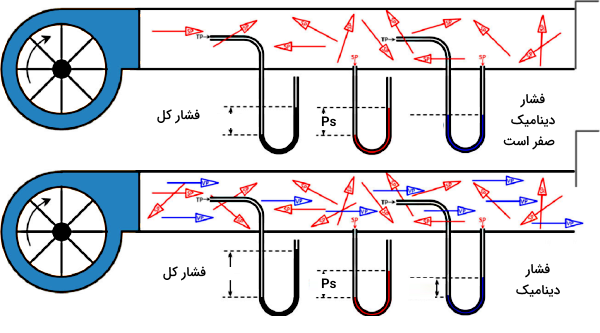
ولی در لوله پایین با باز شدن درب انتهای لوله در سمت چپ تصویر، سیال شروع به جاری شدن میکند و جریان برقرار میشود. چون سیال دارای سرعت است، پس در این مورد فشار دینامیک داریم. همانطور که در شکل مشخص است، داخل لوله علاوهبر پیکانهای قرمز مربوط به فشار استاتیک، پیکانهای آبی فشار دینامیکی هم وجود دارند. فشار دینامیک دارای یک جهت مشخص (همجهت با سرعت سیال) است، در حالی که فشار استاتیک جهت نامشخصی دارد و به دیوارههای لوله به شکل تصادفی وارد میشود. بنابراین در این مورد، فشار کل برابر است با مجموع فشار استاتیک و فشار دینامیک.
پس فشار استاتیک وضعیت فشار سیال آزاد را در حالتی که ساکن است و هیچ نیروی دیگری به آن وارد نمیشود، بررسی میکند. بنابراین تنها نیرویی که به چنین سیالی وارد میشود، نیروی وزن خودش است. طبق تعریف، فشار همان نیرویی است که به سطح وارد میشود. پس فشاری که وزن یا نیروی جاذبه وارد بر سیال ساکن تولید میکند، فشار استاتیک آن است.
مقدار فشار استاتیکی برای یک مایع از رابطه محاسبه میشود که در واقع رابطه ترمودینامیکی فشار برای یک مایع است. خیلی مهم است که هنگام بررسی فشار استاتیک، تفاوت آن را با فشار کل و فشار دینامیک تشخیص دهیم. معمولا همیشه آن فشاری که در هر نقطه از سیال اندازهگیری میشود، فشار استاتیکی است.
فشار چیست؟
برای اینکه بهتر یاد بگیریم فشار استاتیک چیست، لازم است ابتدا ببینیم کمیتی به نام فشار که با حرف P نشان داده میشود، چه مفهومی دارد. تعریف کلی فشار در فیزیک معادل است با اندازه نیروی عمودی وارد بر یک سطح مشخص. پیش از اینکه به ادامه تعریف فشار بپردازیم، چنانچه دانشآموز پایه دهم هستید و میخواهید مبحث فشار در شارهها را بهتر فرابگیرید، لینک مشاهده فیلم آموزشی فیزیک پایه دهم فرادرس برای شما در ادامه قرار داده شده است:
اگر بخواهیم تعریف بالا را در قالب یک فرمول بنویسیم، فشار برابر خواهد شد با:
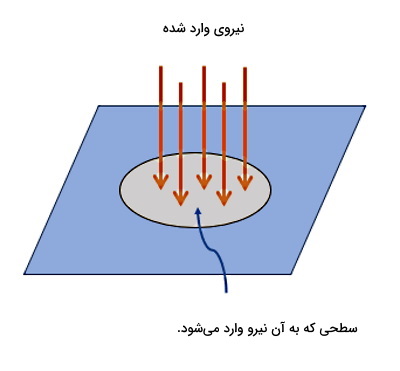
در این رابطه نیروی F بر حسب نیوتن (N) است. همچنین مساحت سطحی (A) که نیرو به آن وارد میشود، بر حسب متر مربع (m۲) است. بنابراین از این فرمول میتوانیم نتیجهگیری کنیم که واحد فشار برابر خواهد شد با نیوتن بر متر مربع یا (). واحد فشار در سیستم بینالمللی یکاها یا SI نیوتن بر متر مربع نیست و نام دیگری دارد.
از فرمول بالا مشخص است رابطه فشار با سطحی که نیرو به آن وارد میشود، معکوس است. هر چه سطحی که نیرو به آن وارد میشود کوچکتر باشد، فشار ایجاد شده بیشتر است. اگر به شکل زیر دقت کنید، با فرض یکسان بودن نیروی وزن آقا و خانم، فشار وارد به پای خانم بیشتر است. چون کفش خانم سطح کمتری دارد و نیروی وارد بر این سطح، فشار بیشتری را ایجاد خواهد کرد.
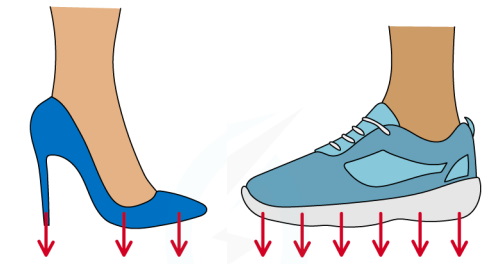
فشار یک کمیت نردهای است، به این معنا که فقط دارای اندازه است و جهت ندارد. با اینکه در فرمول اصلی محاسبه فشار، نیرو وجود دارد که یک کمیت برداری است، اما فشار جهت ندارد. علت این است که در تعریف فشار گفتیم نیروی عمودی، یعنی جهت نیرو خود به خود بهصورت عمود بر سطح در نظر گرفته شده است و در مورد فشار، مسئله فقط اندازه نیروی وارد شده است. معمولا مقادیر فشار از مرتبه کیلوپاسکال هستند. برای مثال مقدار فشار اتمسفر در سطح دریا، ۱۰۱٫۳ kPa است.
رابطه فشار با دما
در بخشهای قبل تا حدی آموختیم که فشار استاتیک چیست و فرمول اساسی فشار را نیز بیان کردیم. در این قسمت میخواهیم ببینیم دما چه اثری روی فشار دارد. هر چه دما بیشتر شود، فشار نیز افزایش خواهد یافت. یعنی رابطه دما و فشار، مستقیم است.
اگر اتاقی با در بسته را در نظر بگیرید، با افزایش دما در این اتاق، انرژی جنبشی مولکولهای هوای داخل اتاق زیاد خواهد شد. بنابراین با افزایش سرعت مولکولهای هوا، فشاری که این مولکولها به دیوارها یا اجسام داخل اتاق وارد میکنند، بیشتر خواهد شد. در شکل زیر با حجم (V) و تعداد مولکولهای (N) برابر، اگر یک محفظه را گرم کنیم، دما (T) و فشار مولکولهای آن بیشتر از دیگری خواهد شد.
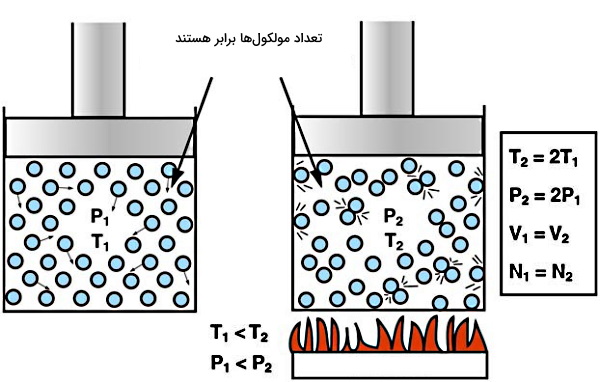
واحد فشار چیست؟
برای اینکه بتوانیم یادگیری خود را در مورد اینکه «فشار استاتیک چیست» بیشتر کنیم، لازم است با واحدهای مختلف فشار نیز کاملا آشنا شویم. واحد استاندارد فشار در سیستم SI «پاسکال» (Pascal) است که با Pa نشان داده میشود. یک پاسکال برابر با یک نیوتن بر متر مربع است.
اما برای نشان دادن مقدار فشار، از واحدهای متنوعی استفاده میشود. علاوهبر پاسکال، واحدهایی مانند بار، اتمسفر، تور، پوند بر اینچ مربع و میلیمتر یا سانتیمتر جیوه از پرکاربردترین واحدهای فشار هستند. طبق آزمایش توریچلی، ارتباط این واحدها بهصورت زیر به دست آمده است:
مرسوم است فشار هوا بر حسب اتمسفر بیان شود و معمولا با P۰ نشان داده میشود، طوری که داریم یا اندازهگیری فشار خون توسط واحد میلیمتر جیوه انجام شود. اگر میخواهید تبدیل واحدهای فشار را بهتر فرابگیرید، مطالعه مطلب «تبدیل واحد فشار – به زبان ساده» از مجله فرادرس اطلاعات خوبی به شما خواهد داد. در جدول زیر تبدیل چند واحد معروف فشار به واحد استاندارد پاسکال و نمادشان بهصورت خلاصه بیان شده است:
| تبدیل به پاسکال | نماد | واحد فشار |
| Pa | پاسکال | |
| bar | بار | |
| torr | تور | |
| atm | اتمسفر | |
| psi | پوند بر اینچ مربع | |
| mmHg | میلیمتر جیوه |
مقدمه یادگیری فشار استاتیک با فرادرس
اگر در مقطع متوسطه مشغول به تحصیل هستید، ممکن است برای یادگیری بهتر فشار استاتیک نیازمند کسب اطلاعات کاملتری در مورد مقدمات این مبحث طبق کتابهای درسی خود باشید. مشاهده فیلمهای آموزشی زیر از فرادرس به شما در تکمیل این مسیر کمک خواهد کرد:
- فیلم آموزش علوم نهم بخش فیزیک فرادرس
- فیلم آموزش فیزیک دهم فرادرس
- فیلم آموزش فیزیک دهم مرور و حل تمرین فرادرس
فشار مایعات
پیش از پرداختن به اینکه فشار استاتیک چیست، لازم است ابتدا با مفهوم «سیال یا شاره» (Fluid) هم آشنا شویم. سیال یا شاره هر مادهای است که بر اثر دریافت نیروی خارجی، همواره جریان دارد و دارای شکل ثابت و مشخصی نیست. با توجه به سه حالت ماده، این تعریف هم مایعات و هم گازها را شامل میشود. علاوهبر مایعات و گازها، پلاسما هم جز انواع سیالات بهشمار میرود. در این بخش فشار مایعات را معرفی میکنیم و به فشار سیالات، در بخشهای بعدی خواهیم پرداخت.
معمولا برای محاسبه فشار مایعات از رابطه بخش قبل استفاده نمیشود، بلکه در مورد مایعات پارامترهای دیگری مانند چگالی، ارتفاع یا عمق آن و شتاب جاذبه زمین مهم میشود. فرمول محاسبه فشار مایعات را میتوانیم از فرمول بخش قبل بهدست آوریم.

فرمول اصلی فشار برابر بود با نیروی عمودی وارد بر سطح. فرض کنید ستونی از یک سیال مایع ساکن داریم. نیرویی که این ستون مایع به سطحی با مساحت A وارد میکند برابر است با نیروی وزن آن. بنابراین میتوانیم بنویسیم:
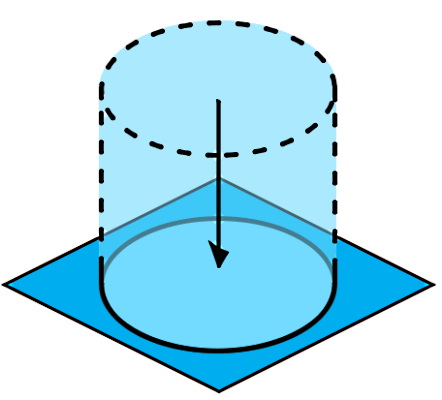
از طرفی جرم مایع را میتوان برحسب چگالی و حجماش بازنویسی کرد:
با جانشینی جرم در فرمول نیروی وزن، برای فشار این نوع سیال ساکن خواهیم داشت:
دقت داریم که برای حجم V از سیال ساکن داریم: . بنابراین فشاری که توسط یک مایع ساکن اعمال میشود، فقط به عمق یا ارتفاع، چگالی آن و شتاب جاذبه زمین بستگی دارد. در واقع فشار یک مایع ساکن، از وزن آن به وجود میآید و با فرمول زیر نشان داده میشود:
که در این رابطه g شتاب جاذبه زمین بر حسب متر بر مجذور ثانیه ()، h ارتفاع بر حسب متر (m) و ρ چگالی مایع بر حسب کیلوگرم بر متر مکعب () است و با فرمول زیر مشخص میشود:
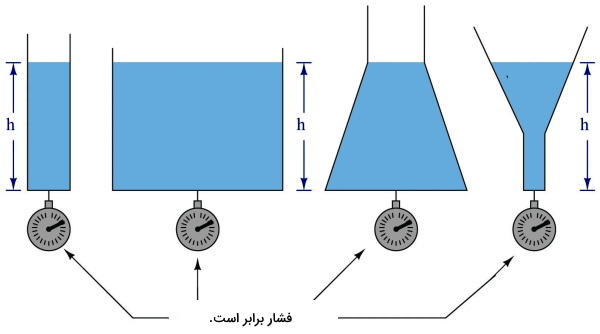
فشار مایع به شکل آن، جرم کل یا مساحت سطح خارجی آن بستگی ندارد. این مسئله را میتوانید در شکل زیر مشاهده کنید. برای مایع مشابهی که در ظروفی با شکلهای مختلف ریخته شده است، مقدار فشار ستون مایع فقط به ارتفاع ظرف بستگی دارد و شکل ظرف مهم نیست. به دلیل برابر بودن ارتفاع ستون مایع، فشار اندازهگیری شده برای هر چهار ستون برابر است.
اصل پاسکال چیست؟
یک مفهوم مهم دیگر برای یادگیری اینکه فشار استاتیک چیست، اصل پاسکال است. فرض کنید سیالی داخل یک ظرف بسته باشد. اگر به یک سمت از این ظرف نیرویی وارد شود، فشار حاصل از این نیرو در تمام نقاط سیال به یک اندازه خواهد بود. این پدیده، اصل پاسکال نام دارد.
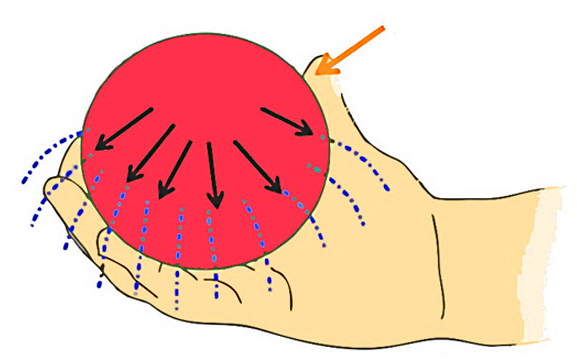
اساس کار ترمزها و جکهای هیدرولیکی، اصل پاسکال است. شکل بالا نمونهای از عملکرد اصل پاسکال است. با فشار دست و وارد شدن نیرو در یک نقطه از توپ، اندازه فشار حاصل از آن در تمام نقاط داخل توپ یکسان است.
فشار سیالات و معادله برنولی
پیش از اینکه ببینیم فرمول فشار استاتیک چیست، در این بخش فشار سیالات را بررسی می کنیم. در بخش قبل دیدیم که فشار مایعات بهعنوان بخشی از سیالات، چگونه محاسبه میشود. فشار سیالات توسط معادله معروفی به نام معادله برنولی محاسبه میشود. معادله برنولی به شکلی که امروز از آن استفاده میکنیم، در سال ۱۷۵۲ توسط «لئونارد اویلر» (Leonhard Euler) ارائه شد.

این معادله نشاندهنده بقای انرژی در سیالات است و اساس دینامیک سیالات «تراکمناپذیر» (Incompressible) بهشمار میرود. منظور از تراکمناپذیری سیال این است که چگالی آن تغییر نمیکند. در کل این مطلب، فرض تراکمناپذیری برقرار است. اگر سرعت سیال خیلی زیاد شود، تراکمپذیری برای سیال رخ میدهد و این معادلات برقرار نخواهند بود.
پیش از اینکه معادله برنولی را مطرح کنیم، لازم است ابتدا شرایط لازم برای برقراری این معادله را بیان کنیم که شامل موارد زیر است:
- صرفنظر کردن از اصطکاک
- عدم امکان تبادل گرما یا کار در مسیر حرکت سیال
- پایا بودن جریان سیال
- تراکمناپذیر بودن سیال
- ناکشسان بودن سیال
حالا با فرض اینکه ρ چگالی سیال، υ سرعت سیال و P فشار سیال است، معادله برنولی به فرم کلی زیر است:
در این رابطه g شتاب جاذبه زمین بر حسب متر بر مجذور ثانیه ()، h ارتفاع سیال بر حسب متر (m)، υ سرعت سیال بر حسب متر بر ثانیه ()، ρ چگالی سیال بر حسب کیلوگرم بر متر مکعب () و P فشار سیال بر حسب پاسکال (Pa) است. b در این فرمول یک عدد ثابت است که به «ثابت برنولی» معروف است.
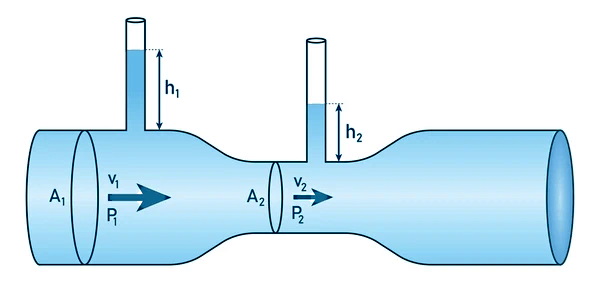
اگر بخواهیم از معادله برنولی در مورد یک سیال استفاه کنیم، میگوییم برای هر دو نقطه یک و دو در یک سیال طبق شکل بالا، همواره رابطه زیر برقرار است:
هد فشار چیست؟
در ادامه یادگیری معادله برنولی جهت پاسخدهی بهتر به این مسئله که فشار استاتیک چیست، مفهوم دیگری به نام «هد فشار» (Head of Pressure) را تعریف میکنیم. هدف از محاسبه چنین کمیتی این است که ارتفاع سیال از سطح مبنا محاسبه شود. هد فشار با تقسیم طرفین معادله برنولی بر شتاب جاذبه زمین (g) به دست میآید:
مرسوم است بهعنوان «وزن مخصوص» (Specific Weight or Unit Weight) سیال در نظر گرفته شود. هر جمله در عبارت بالا را هد مینامیم. برای مثال عبارت و به ترتیب برابر هستند با هد فشار و هد سرعت. بنابراین برای یک سیال، همیشه مجموع سه هد فشار، سرعت و ارتفاع مقدار ثابتی خواهد شد.
بار دیگر به شرایط اولیهای که برای برقراری معادله برنولی لیست کرده بودیم، دقت کنید. در کاربرد معمولا با اصطکاک یا جریانهای کشسان مواجه میشویم و معمولا با چنین سیال ایدهآلی برخورد نداریم. مثلا برای جابجایی سیال داخل لولهها، معمولا از پمپ استفاده میشود که باعث افزایش انرژی سیال خواهد شد یا در صورت وجود اختلاف دما بین سیال و محیط، تبادل گرما رخ میدهد.
برای اینکه این مشکلات برطرف شود و عملا شرایط اولیه دور از واقعیتی نداشته باشیم، از معادله برنولی که بهصورت زیر اصلاح شده است، استفاده میکنیم:
در واقع طرف دوم معادله جدید به جای اینکه مقدار ثابتی شود، برابر با تغییرات گرما و کار است. حرف d که در طرف اول معادله قرار گرفته است، به معنای تغییراتی است که بین هر دو نقطه از مسیر سیال ایجاد میشود. همچنین در رابطه جدید، Q هد مقدار گرمای انتقال داده شده، W هد کار انجام شده و H هد اتلاف انرژی ناشی از اصطکاک است.
اصل برنولی چیست؟
تا اینجا آموختیم که در معادله برنولی، جایگاه فشار استاتیک چیست. در این قسمت بررسی میکنیم معادله برنولی از چه اصولی ناشی میشود. در «مکانیک سیالات» (Fluid Dynamics)، اصل برنولی یک مفهوم مهم و اساسی است که بین سه کمیت مهم فشار، سرعت و ارتفاع ارتباط برقرار میکند. اصل برنولی بیان میکند که با افزایش سرعت یک سیال، همزمان فشار استاتیک یا انرژی پتانسیل آن نیز کم میشود.
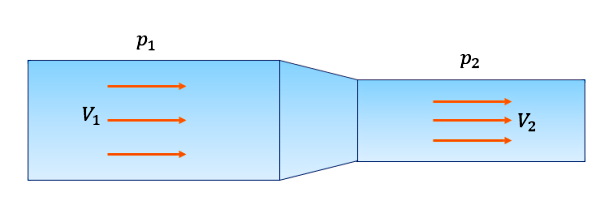
این اصل توسط دانشمند سوییسی به نام «دنیل برنولی» (Daniel Bernoulli) اولین بار مطرح شد. در واقع، اصل برنولی به نوعی همان اصل بقای انرژی در سیالات است. طبق اصل بقای انرژی، برای یک شاره یا سیال پایدار، مجموع انواع انرژیها در تمام نقاطی که چسبندگی ندارند، یکسان است. بنابراین لازم است مجموع انرژی جنبشی، انرژی پتانسیل و انرژی داخلی یکسان باقی بماند.

حالا با در نظر گرفتن انرژیها بهتر میتوانیم اصل برنولی را مجددا بیان کنیم: با افزایش سرعت سیال، انرژی جنبشی آن نیز زیاد میشود. زیاد شدن انرژی جنبشی با کاهش انرژی پتانسیل همراه است و در نتیجه، فشار استاتیکی و انرژی داخلی نیز کم خواهد شد.
این توضیح اصل برنولی برای سیال ساکن بود، یعنی سیالی که داخل یک منبع در حالت سکون است و احتمالا به خاطر ارتفاعی که از سطح زمین دارد، انرژی پتانسیل دارد. به همین دلیل هم با کاهش انرژی پتانسیل، فشار استاتیکی سیال کم خواهد شد. اگر سیال از منبع خارج شده و جاری شود، در این شرایط هم مجموع تمام انواع انرژیها یکی است.
اصل برنولی را میتوان بهصورت مستقیم از قانون دوم نیوتن هم استخراج کرد. اگر حجم خیلی کوچکی از یک سیال بهصورت افقی از یک ناحیه با فشار بالاتر به ناحیهای با فشار پایینتر جاری شود، در این صورت اختلاف فشار باعث خواهد شد نیروی برآیندی به این حجم از سیال وارد شود. این نیرو، طبق قانون دوم نیوتن باعث شتاب گرفتن سیال شود.
اگر بخواهیم مثال ملموسی از اصل برنولی در زندگی واقعی را بیان کنیم، شخصی را فرض کنید که در حال سیگار کشیدن داخل ماشین در حال حرکت است. اگر این شخص پنجره نزدیک به خود را کمی باز کند، دود سیگار بهسرعت از ماشین خارج خواهد شد. به عبارت دیگر، دود سیگار به سمت بیرون مکش میشود. علت این مکش، اختلاف فشار داخل و خارج ماشین است که این اختلاف فشار، به دلیل حرکت ماشین و سرعت آن ایجاد میشود.
روش محاسبه فشار استاتیک
پس از یادگیری معادله برنولی، در این بخش میخواهیم ببینیم کاربرد این معادله در محاسبه فشار استاتیک چیست. یکبار دیگر معادله برنولی و جمله هد فشار را نگاه کنید:
طبق تعریف فشار استاتیک، گفتیم سیال وقتی دارای فشار استاتیک است که ساکن باشد. پس جمله اول در عبارت بالا یا جمله هد سرعت با ساکن بودن سیال و صفر شدن سرعت آن (υ=۰)، صفر می شود. اگر ثابت برنولی در سمت دیگر معادله را نیز صفر در نظر بگیریم، بنابراین جمله هد فشار با ارتفاع سیال برابر خواهد شد. اگر قدر مطلق این برابری را در نظر بگیریم، خواهیم داشت:

پس محاسبه هد فشار، ارتفاعی از سیال را به ما میدهد که اگر تمام نیروهای وارد بر سیال را حذف کنیم (برای مثال نیروهایی مانند مقاومت هوا یا اصطکاک، بهجز نیروی وزن سیال)، سیال به اندازه این ارتفاع بالا میرود. همچنین از عبارت بالا میتوانیم نتیجهگیری کنیم که هد فشار از جنس طول است.
پس یک روش محاسبه فشار استاتیک این است که هد فشار را محاسبه کنیم. یعنی فشار را بر وزن مخصوص سیال تقسیم کنیم.چنین روشی در نهایت ما را به فرمول محاسبه فشار مایعات میرساند:
در این محاسبات باید به تفاوت وزن مخصوص سیال و چگالی سیال دقت کنیم. وزن مخصوص همانطور که گفتیم برابر است با حاصلضرب شتاب جاذبه زمین در چگالی سیال. بهعبارتی وزن مخصوص سیال برابر است با نسبت وزن سیال به حجم آن:
در حالی که چگالی سیال برابر است نسبت جرم سیال به وزن آن. پس چگالی سیال (ρ) از شتاب جاذبه زمین مستقل است اما وزن مخصوص سیال (γ) به شتاب گرانش زمین وابسته است.
روش دیگر محاسبه فشار استاتیک، استفاده از فرمول پایه است. در بخشهای قبل، ثابت کردیم که فرمول فشار مایعات هم به نوعی معادل همین فرمول است. بنابراین فرمولها تقریبا یکی هستند. چیزی که برای پیدا کردن فشار استاتیک مهم است این است که توجه داشته باشیم فشار استاتیک، در شرایط سکون سیال محاسبه میشود. در بخش بعد مفاهیم فشار کل و فشار دینامیک را شرح میدهیم تا به درک درستتری از فشاراستاتیک برسیم.
فشار دینامیک چیست؟
تشخیص اینکه فشار استاتیک چیست، زمانی دقیقتر اتفاق میافتد که بدانیم فشار دینامیک چیست و این دو چه تفاوتی با هم دارند. اهمیت فشار دینامیک از این جهت است که میتواند یک پیشبینی از مقدار سرعت سیال در اختیار ما قرار دهد. اگر به معادله برنولی دقت کنیم، یک جمله در این معادله وجود داشت که به سرعت سیال وابسته بود. این جمله، همان فشار دینامیک است.

همانطور که در شکل بالا مشخص است، فشار دینامیک به سرعت سیال بستگی دارد، در حالی که فشار استاتیک مستقل از اینکه سرعت سیال چقدر است، فشاری است که اگر سیال ساکن بود باز هم به دیوارههای لوله وارد میشد. پس فشار دینامیک بیانگر فشار یک سیال در حال جریان با سرعت υ است. برای یک سیال تراکمناپذیر طبق معادله برنولی، فشار دینامیک برابر است با:
که در آن q مقدار فشاردینامیکی بر حسب پاسکال (Pa)، ρ چگالی سیال بر حسب کیلوگرم بر متر مکعب () و υ سرعت سیال بر حسب متر بر ثانیه () است. بنابراین برخلاف فشار استاتیک که فشار سیال در حالت سکون بررسی میشد، فشار دینامیک شرایط سیال را در حالتی که با سرعتی مثل سرعت υ در جریان است، بررسی میکند. به همین علت، این فشار به «فشار سرعت» (Velocity Pressure) هم معروف است.
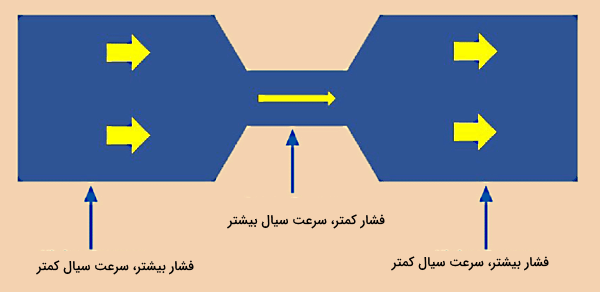
اگر به معادله برنولی دقت کنیم، با توجه به ثابت بودن طرف دوم معادله، مشخص است که در نقاطی که سرعت سیال زیاد است، فشار دینامیکی بیشتر و در نتیجه مقدار فشار استاتیکی کمتر است. معمولا در سیستمهای لولهکشی افت فشار ناشی از وجود تجهیزاتی مثل شیر یا زانویی، از کاهش سرعت سیال و در نتیجه کاهش فشار دینامیک ناشی میشوند.
فشار کل چیست؟
حالا که متوجه شدیم تفاوت فشار دینامیک و فشار استاتیک چیست، میتوانیم تعریف مجموع این دو فشار، یعنی فشار کل را بیان کنیم. برای اینکه تفاوت دو مفهوم فشار استاتیک و فشار کل را بهتر متوجه شوید، در این بخش ابتدا چند موقعیت مختلف را بهعنوان مثال توضیح میدهیم و سپس در قالب فرمول، تمایز این سه نوع فشار را بررسی میکنیم.
فرض کنید روی یک سطح سیالی داریم که در حالت سکون است، یعنی حرکتی ندارد. میدانیم داخل سیال، مولکولهای بیشماری وجود دارند که در حال حرکت در جهتهای مختلف بهصورت کاتورهای یا تصادفیاند. بنابراین در هر نقطهای از این سیال ساکن، هر مولکول میتواند به سطحی که سیال روی آن قرار دارد، نیرویی وارد کند و در نتیجه در هر نقطه فشار استاتیکی داریم.
حالا اگر فرض کنیم همین سیال داخل یک لوله قرار بگیرد و جریان داشته باشد، این سیال دیگر ساکن محسوب نمیشود. در این شرایط همچنان هر مولکول دارای حرکات تصادفی است و به سطح بالا و پایین لوله نیرویی وارد میکند که فشار استاتیکی را ایجاد خواهد کرد. اگر در انتهای این لوله دربی قرار داده شود، تمام مولکولها در انتهای لوله به این درب نیرویی وارد خواهند کرد. نیروی وارد بر درب، فشار کل را ایجاد میکند.
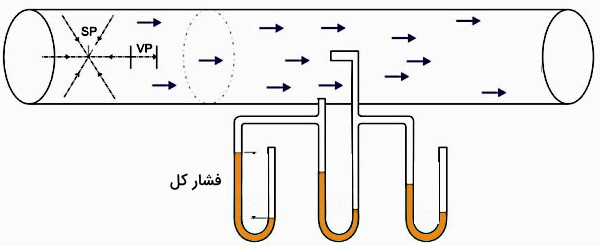
اجازه دهید یک مثال ملموستر بیان کنیم. فرض کنید زنبوری در یک ماشین، در حال بال زدن در جهتهای مختلف و تصادفی است. این ماشین با سرعتی حدود ۶۰ کیلومتر بر ساعت در حال حرکت به سمت راست است. شما در صندلی جلو در حال رانندگی هستید، در حالی که زنبور پشت سر شما در حال بال زدن است. قاعدتا زنبور هم با سرعت ۶۰ در حال حرکت به سمت راست است.
حرکت زنبور در جهتهای مختلف متناظر با فشار استاتیکی است. حالا فرض کنید یک پنجره ماشین را باز میکنید و در حالی که یک نفر بیرون ایستاده است، زنبور به خارج از ماشین حرکت میکند. اگر زنبور با این شخص برخورد کند، احتمالا این شخص نیروی خیلی قوی را حس خواهد کرد. نیرویی که این شخص حس میکند، اثر فشار کل است.
محاسبه فشار کل از معادله برنولی
در مکانیک سیالات، فشار کل برای یک سیال در حال جریان با P0 نشان داده میشود و برابر است با مجموع فشار استاتیک و فشار دینامیک یک جریان آزاد:
- : فشار استاتیکی
- : فشار دینامیکی یا q
- : فشار کل
در رابطه بالا، ممکن است مقادیر فشار استاتیکی و دینامیکی در نقاط مختلف سیال تغییر کنند ولی فشار کل در شرایطی که کار خارجی یا انتقال حرارت در سیستم نداشته باشیم، ثابت است. به فشار کل، «فشار سکون یا ایستایی» (Stagnation Pressure) یا «فشار پیتوت» (Pitot Pressure) هم گفته میشود. علت نامگذاری فشار کل به فشار سکون این است که در نقطه سکون، سرعت سیال صفر است و تمام انرژی جنبشی سیال به فشار تبدیل شده است.
اگر بخواهیم ببینیم رابطه بالا چطور از معادله برنولی بهدست آمده است، دو نقطه هم ارتفاع داخل یک سیال فرضی تراکمناپذیر را در نظر میگیریم که یکی از این نقاط دقیقا منطبق بر نقطه سکون است. معادله برنولی به شکل زیر است:
برای دو نقطه موردنظر باید این معادله برقرار باشد. پس خواهیم داشت:
دقت داریم که در رابطه بالا چگالی و ارتفاع برای هر دو طرف یکسان است. پس میتوانیم جملات وسط هر دو طرف را حذف کنیم:
اگر فرض کنیم نقطه ۲، نقطه سکون است، پس υ۲=۰ و فشار این نقطه برابر با Pstagnation خواهد شد. بنابراین طرف دیگر معادله به ما مقادیر فشار استاتیک و فشار دینامیک را خواهد داد:
بنابراین با دانستن فشار کل، میتوانیم بگوییم فشار دینامیک برابر میشود با اختلاف مقادیر فشار کل و فشار استاتیک. در بخشهای بعد با حل مثال و استفاده از روابط، تفاوتهای این سه نوع فشار را بهتر متوجه خواهید شد.
روش اندازهگیری فشار استاتیک
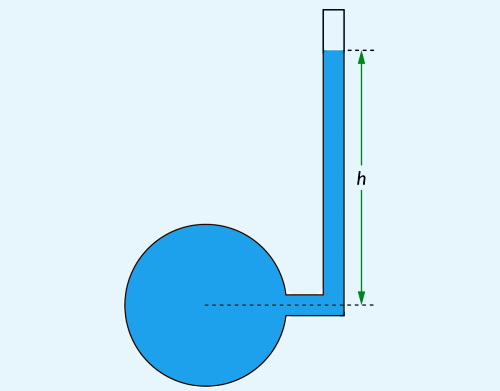
در بخشهای گذشته توضیح دادیم که فرمول محاسبه فشار استاتیک چیست. گفتیم هد فشار بیانگر ارتفاعی است که یک سیال در صورت حذف نیروهای خارجی دیگر، میتواند نسبت به سطح مبنا برخلاف جاذبه زمین بالا رود. پس اندازهگیری این ارتفاع، به نوعی محاسبه هد فشار یا فشار استاتیک است. یک ابزار ساده جهت اندازهگیری این ارتفاع، «پیزومتر» (Piezometer) است.
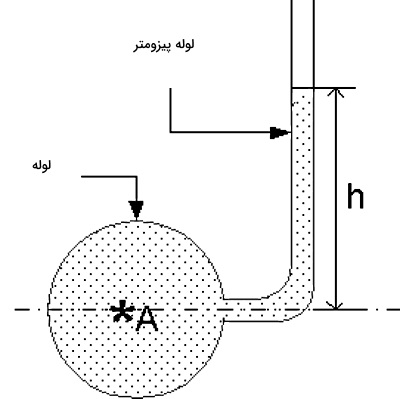
پیزومتر ابزاری است که برای اندازهگیری فشار مایعات در یک سیستم طراحی شده است، به این صورت که ارتفاعی که ستون مایع بر خلاف جاذبه بالا میرود، را اندازه میگیرد. این ابزار ساده از یک لوله شیشهای تشکیل شده است که یک سر آن، به خط لوله وصل است و فشار این قسمت قرار است اندازهگیری شود. اما سر دیگر آن طبق شکل بالا، در معرض فشار هوا یا فشار اتمسفر قرار میگیرد. در این وسیله ارتفاعی که مایع در لوله بالا میرود، هد فشار را به دست میدهد.
دقت کنید پیزومتر نمیتواند مقادیر منفی فشار یا فشار خلا را محاسبه کند. همچنین همانطور که گفتیم، پیزومتر فقط فشار مایعات را میسنجد و برای اندازهگیری فشار گازها بکار نمیرود. علت این است که یک سر این لوله در معرض فشار اتمسفر است و گازها سطح آزاد ندارند. بیشترین کاربرد پیزومتر، در اندازهگیری فشار آب داخل یک ظرف است. در پیزومتر شکل بالا، با اندازهگیری ارتفاع h، فشار استاتیک مایع در نقطه A محاسبه میشود.
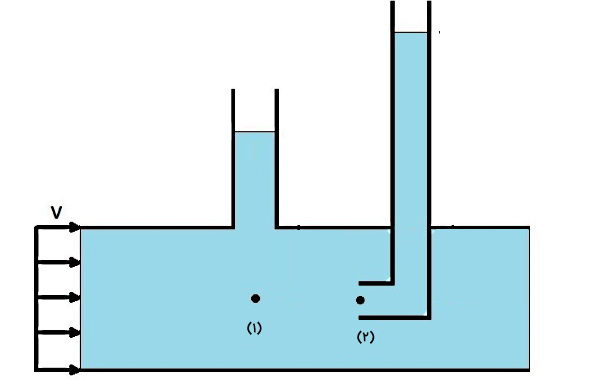
این ابزار جهت اندازهگیری فشار استاتیک طراحی شده است و با «لوله پیتوت» (Pitot Tube) متفاوت است. برای اینکه تفاوت پیزومتر با لوله پیتوت را بهتر متوجه شوید، در ادامه سیستم اندازهگیری فشار کل را توضیح میدهیم. معمولا برای اندازهگیری فشار کل، از سیستمی متشکل از دو لوله (Pitot-static Tubes)، به نام لوله پیتوت و لوله فشار استاتیک یا همان پیزومتر استفاده میشود. در شکل زیر، سیستم اندازهگیری فشار سکون نشان داده شده است.
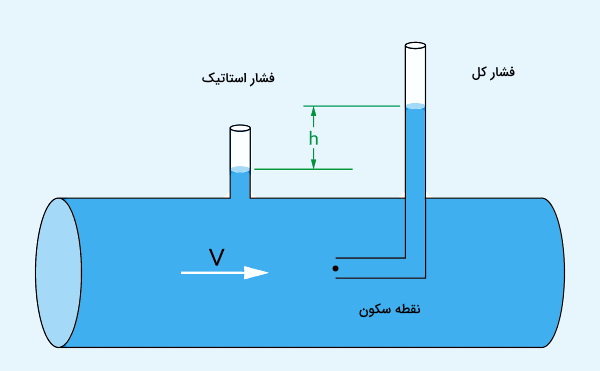
اگر به محل قرارگیری این دو لوله توجه کنید، لوله استاتیک یا همان پیزومتر در دیواره ظرف قرار میگیرد (لوله خارجی)، در حالی که لوله پیتوت (لوله داخلی) داخل سیال و در معرض سرعت آن قرار میگیرد. یعنی لوله پیتوت، ارتفاع سیال را از محور میانی لوله در نظر میگیرد. این دو لوله سرعت سیال را محاسبه میکنند و با محاسبه سرعت، فشار کل نیز محاسبه خواهد شد.
حل مثال فشار استاتیک
در این بخش با حل چند مثال، به شما کمک میکنیم تا بهتر متوجه شوید که فشار استاتیک چیست و چگونه محاسبه میشود.
مثال ۱
فرض کنید ظرف استوانهای شکلی با ارتفاع ۳ m و شعاع ۰٫۲۵ m داریم که درب بالایی آن نیز بار است. داخل این ظرف از مایعی که نمیدانیم دقیقا چیست، کاملا پر شده است. جرم مایعی که داخل ظرف است، چقدر است؟ (فرض کنید فشار ته ظرف ۱٫۲ atm است)
پاسخ
با توجه به شرایط مسئله، مایع در حالت سکون است. همچنین چون نکته دیگری در صورت سوال بیان نشده است، بنابراین سیال این سوال، مایعی است تراکم ناپذیر، یعنی چگالی آن در سرتاسر ارتفاع ظرف یکسان خواهد بود. از فرمولی که در بخش پیش گفتیم، استفاده میکنیم:
در این رابطه P فشار ته ظرف است که مقدارش در صورت سوال ۱٫۲ atm است. این فشار که همان فشار کل است برابر خواهد بود با مجموع فشار ستون مایع به ارتفاع ۳ m و فشاری که محیط به سطح مایع وارد میکند. چون در سوال ذکر شده بود که درب بالایی طرف باز است، پس این فشار وجود دارد و برابر است با P۰. میدانیم مقدار P۰ برابر با ۱ atm است.
اما نکته مهم این است که باید هر دو مقدار فشاری که داریم از اتمسفر به پاسکال تبدیل شوند و بعد در فرمول بالا قرار داده شوند. از بخش تبدیل واحدها میدانیم که . پس داریم:
حالا این دو مقدار فشار را در فرمول اول قرار میدهیم:
دقت داریم که حجم مایع برابر است با حجم ظرفی که در آن ریخته شده است. ظرف استوانهای دارای حجمی بهصورت زیر است:
مثال ۲
در شکل زیر مشاهده میکنید که یک لوله پیتوت و یک پیزومتر به یه لوله آب افقی متصل شدهاند. سرعت آب در مرکز لوله را محاسبه کنید:
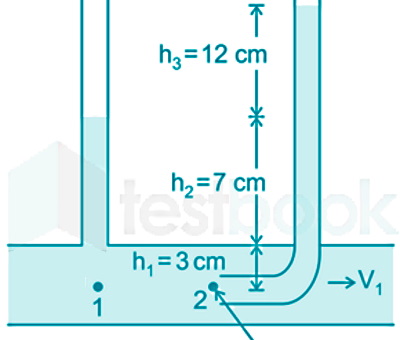
پاسخ
برای اینکه به این سوال بهتر پاسخ دهیم، از معادله برنولی یا همان اصل برابری فشار کل در هر دو نقطه استفاده میکنیم. اگر دو نقطه در سیال انتخاب کنیم، یکی در نقطه ۱ طبق شکل و دیگری در نقطه ۲ که کاملا منطبق بر نقطه سکون است، آنگاه خواهیم داشت:
مقدار چگالی برای دو طرف رابطه بالا یکسان است. پس از دو طرف ρ را حذف میکنیم. در نقطه ۲ که همان Stagnation Point یا نقطه سکون است، سرعت سیال مساوی با صفر است. همچنین ارتفاع سیال در این نقطه ۱۹ cm است که برابر میشود با ۰٫۱۹ m. در نقطه ۱ نیز ارتفاع آب ۷ cm یا ۰٫۰۷ m است. دقت کنید حتما باید تبدیل واحدها به واحدهای استاندارد انجام شود. با قرار دادن این مقادیر در فرمول بالا خواهیم داشت:
انواع دیگر فشار
پس از اینکه آموختیم فشار استاتیک چیست و دو نوع فشار مهمی که با فشار استاتیک رابطه دارند، یعنی فشار کل و فشار دینامیک را نیز شرح دادیم، در این بخش میخواهیم ببینیم انواع دیگر فشار به چه صورت هستند. آشنایی با انواع دیگر فشار، در تشخیص فشار استاتیک کمککننده خواهد بود. بنابراین در ادامه «فشار مطلق» (Absolute Pressure) و «فشار گیج» (Gauge Pressure) را توضیح خواهیم داد.
فشار مطلق چیست؟
اگر بخواهیم بهدرستی تشخیص دهیم که فشار استاتیک چیست، باید انواع فشار را بشناسیم. مجموع فشارهای وارد بر یک سطح یا جسم، فشار مطلق نامیده میشود. در حالی که فشار گیج یا Gauge Pressure از فشار اتمسفر سنجیده میشود، فشار مطلق نسبت به صفر مطلق اندازهگیری میشود. شکل زیر تفاوت این دو نوع فشار را بهتر نشان میدهد.
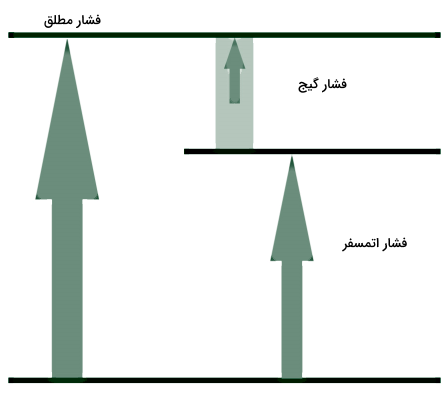
فشار پیمانهای یا فشار گیج چیست؟
در ادامه روند تشخیص اینکه فشار استاتیک چیست، در این قسمت فشار گیج را توضیح میدهیم. فشار گیج یا فشار پیمانهای فشاری است که معمولا در فشارسنجها نشان داده میشود. چون این فشار نسبت به فشار محیط سنجیده میشود، آن را «فشار نسبی» (Relative Pressure) هم مینامند. همچنین، نام دیگر این فشار، «فشار مانومتریک» (Manometric Pressure) است. با توجه به تعریفی که برای فشار مطلق داشتیم، فشار نسبی برابر است با فشار مطلق یک محفظه منهای فشار اتمسفر.
اندازهگیری فشار نسبی توسط ابزارهایی به نام گیج فشار یا «مانومتر» (Manometer) انجام میشود که تصویر آن را در زیر مشاهده میکنید. در این وسیله عقربهای وجود دارد که تحت اثر فشار اعمال شده دچار انحراف میشود و به این صورت، فشار را اندازه میگیرد. این ابزار برای اندازهگیری مقادیر بالای فشار و در شرایطی که دقت چندان زیادی هم نیاز نیست، بکار میرود.

معمولا در داخل لولههای بزرگ یا دیگهای بخار که گیجهای لولهای مستقیم مانند پیزومتر بهراحتی وصل نمیشوند، از این ابزار استفاده میشود. پیزومتر، سادهترین فرم یک مانومتر یا گیج فشار محسوب میشود.
یادگیری فشار استاتیک با فرادرس
در این مطلب یاد گرفتیم فشار استاتیک چیست، چگونه محاسبه میشود و چه تفاوتهایی با فشار کل و فشار دینامیکی دارد. چنانچه علاقهمندید یادگیری خود در مورد فشار استاتیک را با حل تمرینها و مثالهای مختلف و بررسی کاربرد آن در مباحث مکانیک سیالات توسعه دهید یا با سوالات چهار گزینهای در مورد این مبحث بیشتر آشنا شوید، مشاهده فیلمهای آموزشی زیر از فرادرس را به شما پیشنهاد میکنیم:
- فیلم آموزش فیزیک پایه ۳ فرادرس
- فیلم آموزش فیزیک ۳ حل تمرین فرادرس
- فیلم آموزش مکانیک سیالات ۱ فرادرس
- فیلم آموزش مکانیک سیالات ۱ مرور و حل تمرین فرادرس
- فیلم آموزش مکانیک سیالات مرور و حل تست کنکور ارشد فرادرس
- فیلم آموزش مقدماتی مکانیک سیالات ۲ فرادرس
جمعبندی
در این مطلب از مجله فرادرس یاد گرفتیم که فشار استاتیک چیست و چه ارتباطی با فشار دینامیک و فشار کل یک سیال دارد. برای یک جریان سیال، فشار استاتیک فشار سیال در شرایطی است که سیال در حالت سکون است. فشار استاتیک در واقع فشاری است که سیال به واسطه وزن خود دارد. مشخصه این فشار، ارتفاعی است که سیال در یک لوله در صورت حذف تمام نیروهای وارد بر آن، بالا میرود.
اما فشار دینامیک فشاری است که وقتی سیال شروع به حرکت میکند، ایجاد میشود. این فشار با سرعت سیال یا υ رابطه مستقیم دارد. فشار کل، مجموع فشار استاتیک و فشار دینامیک سیال است. اندازهگیری فشار استاتیک، توسط یک لوله ساده به نام پیزومتر انجامپذیر است.
آزمون فشار استاتیک
اگر میخواهید میزان یادگیری خود در مورد اینکه فشار استاتیک چیست را محک بزنید، در این بخش آزمونی را برای شما تهیه کردهایم. پس از پاسخدهی به سوالات آزمون، با کلیک بر روی بخش «دریافت نتیجه آزمون» میتوانید نمره نهایی خود را مشاهده کنید.
تمرین و آزمون
کدام گزینه در مورد پیزومتر اشتباه است؟
پیزومتر ابزاری است که فشار مایعات را با محاسبه ارتفاعی که مایع در ستون لوله برخلاف جاذبه بالا میرود، اندازهگیری میکند.
پیزومتر ابزاری است که برای محاسبه فشار استاتیک طراحی شده است.
لوله پیزومتر برخلاف لوله پیتوت، داخل جریان سیال هیچگونه جهتگیری ندارد.
پیزومتر به همراه لوله پیتوت در اندازهگیری فشار استاتیک بکار میرود.
گزینه آخر اشتباه است. لوله پیزومتر به همراه لوله پیتوت، فشار کل را اندازه میگیرد.
فشار اندازهگیری شده توسط یک لوله پیتوت، ۱۰۰ kPa است.اگر سرعت جریان آب داخل آن ۹ m/s باشد، فشار استاتیک آب تقریبا برابر با کدام گزینه است؟
گزینه اول درست است. لوله پیتوت فشار کل را اندازه میگیرد. بنابراین اگر فرمول فشار کل را برحسب فشار دینامیکی (سرعت سیال) و فشار استاتیک بنویسیم، خواهیم داشت:
مقدار فشار کل و سرعت سیال را در صورت سوال داریم. همچنین مشخص است که سیال در این سوال آب است. پس چگالی سیال نیز مشخص شد که برابر است با . با جایگذاری مقادیر عددی در فرمول بالا، خواهیم داشت:
دقت کنید برای مقدار فشار کل، حتما باید تبدیل واحد کیلوپاسکال به پاسکال در فرمول اعمال شود.
فشاری که به دلیل حرکت سیال ایجاد میشود، ... نام دارد.
فشار استاتیک
فشار کل
فشار دینامیک
فشار سکون
گزینه درست، گزینه دوم است. گفتیم که فشاری که شرایط سیال در حالت سکون را بررسی میکند، فشار استاتیک نام دارد. اگر سیال شروع به حرکت با سرعت υ کند، فشار دینامیک ایجاد خواهد شد. فشار کل یا فشار سکون نیز مجموع فشار دینامیک و استاتیک است.
اگر در نقطهای از یک سیال سرعت سیال دو برابر شود، فشار استاتیکی و دینامیکی آن چقدر خواهد شد؟
فشار استاتیکی نصف و فشار دینامیکی چهار برابر میشود.
فشار استاتیکی نصف و فشار دینامیکی دو برابر میشود.
فشار استاتیکی یک چهارم و فشار دینامیکی چهار برابر میشود.
فشار استاتیکی یک چهارم و فشار دینامیکی دو برابر میشود.
پاسخ درست گزینه سوم است. از فرمول فشار دینامیکی بهصورت ، مشخص است که رابطه فشار دینامیکی با سرعت سیال به شکل توان دوم است. یعنی اگر سرعت سیال در نقطهای دو برابر شود، فشار دینامیکی برابر خواهد شد. پس فشار دینامیکی چهار برابر میشود.
از طرفی طبق معادله برنولی، میدانیم مقدار فشار کل ثابت است. پس اگر فشار دینامیکی زیاد شود، فشار استاتیک هم به همان اندازه کاهش یافته است. بنابراین فشار استاتیکی یک چهارم برابر شده است.
فرض کنید سیالی داخل یک لوله بسته قرار دارد. اگر یک انتهای لوله باز شود و سیال شروع به حرکت کند، کدام گزینه در مورد فشار کل این دو موقعیت صحیح است؟
همواره فشار کل برابر است با مجموع فشار استاتیک و فشار دینامیک سیال.
ابتدا فشار کل برابر است با مجموع فشار استاتیک و فشار دینامیک. بعد از باز شدن یک انتهای لوله، فشار کل همان فشار استاتیک است.
ابتدا فشار کل با فشار استاتیک برابر است. بعد از باز شدن یک انتهای لوله، فشار کل برابر است با مجموع فشار استاتیک و فشار دینامیک سیال.
هیچکدام
برای سیالی با سرعت υ در حال حرکت داخل یک لوله است، کدام فشار وجود دارد؟
فشار کل
فشار دینامیک
فشار استاتیک
همه موارد
فشار مایعات به کدام گزینه بستگی دارد؟
ارتفاع مایع
شکل ظرفی که مایع در آن است.
مساحت سطح مقطع ظرفی که مایع در آن است.
هیچکدام
در نقطه سکون داخل یک سیال، سرعت سیال کدام است؟
بیشترین مقدار
کمترین مقدار
صفر
مشخص نیست.
فشار استاتیک مایعی به چگالی a و ارتفاع b در یک ستون در بسته چقدر است؟
برای سیال جاری در یک لوله که شرایط اصل برنولی را دارد، اگر در نقطهای سرعت سیال زیاد شود، فشار استاتیکی آن ... میشود.
کم
زیاد
هیچکدام
نمیتوان مشخص کرد.













عرض دیگه هم اینکه
به نظر میاد در پاسخ سؤال چهارگزینه ای که مطرح شد:
“ فشاری که به دلیل حرکت سیال ایجاد میشود، … نام دارد.”
پاسخ گزینه “فشار دینامیکی” باشد؟!
لطفا در صورت امکان راهنمایی بفرمایید
با تشکر فراوان
سلام خدمت شما؛
بله اصلاح گزینه درست انجام شد.
از دقت نظر شما سپاسگزاریم.
با سلام و احترام؛
ضمن تشکر از تدریس روان و بی نظیرتون،
سؤالی که داشتم در مورد شکل با captain
“مجموع فشار استاتیک (SP) و فشار دینامیک (VP) برابر است با فشار کل (TP) وارد بر انتهای لوله”
اینه که چطور ممکنه فشار استاتیکی و فشار دینامیکی از فشار کل بیشتر باشند؟
متشکرم
با سلام خدمت شما؛
نکته بیان شده صحیح است و اصلاحات لازم در تصویر اعمال شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
درود بر شما
اگر یک گیج بالای یک لوله وصل شود و سیال در داخل لوله در حال حرکت باشد چه فشاری اندازه گیری میشود؟لوله افقی و گیج عمود بر لوله نصب شود
با سلام خدمت شما؛
گیج مجموع هر دو فشار یعنی فشار دینامیکی و فشار استاتیکی که همان فشار کل است را اندازهگیری میکند. دقت کنید در اینجا منظور ما از فشار کل با فشار کلی که از مجموع فشار مطلق و فشار پیمانهای بهدست میآید، متفاوت است.
از همراهی شما با مجله فرادرس سپاسگزاریم.
توی مثال اخر گفتین ارتفاع اول ۷ و نقشه دوم ۱۹ هست در حالی که ارتفاع ۱۰ و ۲۲ هست
در ثانی اگر ارتفاع یکی نیست چرا در اثبات فرمول فشار کل ارتفاع را یکسان گرفتین
با سلام خدمت شما؛
در اثبات فشار کل، منظور ما از ارتفاع h که از دو طرف ساده شده است، فاصله بین هر کدام از نقاط ۱ یا ۲ تا بالای لوله است. این فاصله برای هر دو نقطه یکسان است. در این مثال هم این فاصله که معادل با ۳ سانتیمتر است، برای هر دو نقطه یکی است. به همین خاطر در محاسبات خود آن را در نظر نمیگیریم و از اعداد ۷ و ۱۹ بهجای ۱۰ و ۲۲ استفاده میکنیم. لازم به ذکر است که اگر بهجای ۷ و ۱۹ از ۱۰ و ۲۲ استفاده شود، باز هم نتیجه یکی است. کاربرد این روش معادل این است که در اثبات فرمول فشار کل، دو عبارت pgh را از طرفین ساده نکنیم و به جای آنها عدد قرار دهیم.
از همراهی شما با مجله فرادرس متشکریم.