فرمول شتاب چیست؟ – به زبان ساده + حل مسئله

به هنگام صحبت در مورد حرکت جسمی بر خط راست، از مفاهیمی به نام سرعت و شتاب استفاده میکنیم. در حالت کلی، سرعت و شتاب به اشتباه به جای یکدیگر استفاده میشوند، اما مفهوم این دو کمیت در فیزیک به طور کامل متفاوت است. در این مطلب، فرمول شتاب لحظهای و متوسط را با ذکر مثالهای مختلف توضیح میدهیم. همچنین، برای داشتن درک بهتری از مفهوم شتاب، تفاوت آن را با سرعت بیان میکنیم.
فرمول شتاب چیست ؟
فرمول شتابهای مختلف در جدول زیر به طور خلاصه آورده شده است.
| نوع شتاب | فرمول شتاب |
| شتاب متوسط | |
| شتاب لحظهای | |
| شتاب و نیرو | |
| شتاب گرانش | |
| شتاب مرکزگرا |
قبل از توضیح در مورد فرمول شتاب، ابتدا در مورد مفهوم این کمیت و تفاوت آن با سرعت، صحبت میکنیم.
تفاوت سرعت و شتاب چیست ؟
سرعت برابر تغییرات مکان جسم نسبت به زمان است، در حالیکه شتاب به صورت تغییرات سرعت نسبت به زمان تعریف میشود. جسمی را در مکان A در نظر بگیرید. این جسم در مدت زمان t، از نقطه A به نقطه B میرود. تغییر مکان این جسم از نقطه A به نقطه B، نسبت به مدت زمان این تغییر مکان، برابر سرعت حرکت جسم است.

تعریف سرعت به زبان ریاضی برابر است با:
رابطه فوق، سرعت متوسط یا سرعت حرکت جسم را در بازه زمانی t میدهد. اما سوالی که ممکن است مطرح شود آن است که سرعت در هر لحظه از زمان از چه رابطهای بهدست میآید. برای محاسبه سرعت لحظهای، زمان را به سمت صفر میبریم:
به عنوان مثال، اتومبیلی را فرض کنید که با سرعت 48 کیلومتر بر ساعت به سمت شرق حرکت میکند. سرعت، کمیتی برداری است. بنابراین جهت بردار سرعت به سمت شرق و اندازه آن برابر ۴۸ کیلومتر بر ساعت خواهد بود. این اتومبیل در هر ساعت، ۴۸ کیلومتر به سمت شرق حرکت میکند. پس از گذشت ۲ ساعت، اتومبیل ۹۶ کیلومتر به سمت شرق حرکت کرده است. در نتیجه، سرعت به ما میگوید مکان جسم با چه نرخی تغییر میکند.
به تغییرات سرعت در مدت زمان مشخصی، شتاب گفته میشود و با استفاده از فرمول زیر بهدست میآید:
شتاب متوسط حرکت جسم است. برای بهدست آوردن شتاب لحظهای، زمان را به سمت صفر میبریم:
جسمی را فرض کنید که با شتابی برابر ۸ متر بر مجذور ثانیه ( حرکت میکند. اکنون به جدول زیر دقت کنید. مقدار افزایش سرعت در هر ثانیه برابر ۸ است. به مقدار افزایش سرعت در هر ثانیه، شتاب گفته میشود.
| زمان | سرعت |
| 0 | 0 |
| ۱ | |
| 2 | |
| 3 | |
| ۴ |
فرمول شتاب و سرعت چیست ؟
تا اینجا با تعریف سرعت و شتاب و رابطههای آنها به طور کلی آشنا شدیم. در ادامه، فرمولهای محاسبه سرعت و شتاب را با جزییات بیشتری بررسی میکنیم.
اگر جسمی در زمان در مکان و در زمان در مکان قرار داشته باشد، سرعت حرکت آن در فاصله زمانی تا به صورت زیر بهدست میآید:
سرعت بهدست آمده با استفاده از رابطه فوق، سرعت متوسط نام دارد. حال اگر بازه زمانی را بسیار کوچک و را به نزدیک کنیم، سرعت در هر لحظه بهدست خواهد آمد. برای داشتن درک عمیقتری از این موضوع، نمودار مکان بر حسب زمان، در تصویر زیر را در نظر بگیرید. برای محاسبه سرعت متوسط از روی نمودار مکان-زمان، شیب خط متصلکننده دو نقطه و را بهدست میآوریم. در مقابل، برای محاسبه سرعت لحظهای، زمانهای و ، به یکدیگر نزدیک میشوند. بنابراین، به جای محاسبه شیبِ خط متصلکننده دو نقطه، شیب نمودار در نقطه دلخواه را بهدست میآوریم.
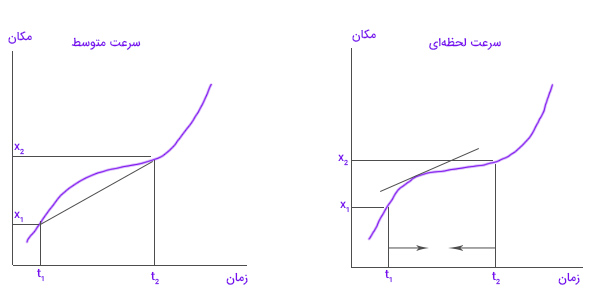
- نکته ۱: اگر شیب نمودار مکان-زمان در هر نقطه ثابت باشد، جسم با سرعت ثابت حرکت میکند. بنابراین، سرعت متوسط و سرعت لحظهای آن با یکدیگر برابر هستند.
- نکته ۲: اگر شیب نمودار مکان-زمان، منفی باشد، سرعت جسم با گذشت زمان، کاهش مییابد.
- نکته ۳: اگر شیب نمودار مکان-زمان، مثبت باشد، سرعت جسم با گذشت زمان، افزایش مییابد.
- نکته ۴: اگر سرعتهای متوسط و لحظهای با یکدیگر برابر باشند، حرکت جسم، حرکت با سرعت ثابت نام دارد.
شتاب را به صورت تغییرات سرعت بر حست مدت زمان آن تغییرات، تعریف کردیم. اگر سرعت جسمی در زمان برابر و در زمان برابر باشد، شتاب حرکت آن در فاصله زمانی تا به صورت زیر بهدست میآید:
رابطه فوق، تعریف شتاب متوسط است، زیرا شتاب در بازه زمانی محدودی محاسبه میشود. برای بهدست آوردن شتاب لحظهای، نرخ تغییرات سرعت را در لحظهای مشخص بهدست میآوریم. برای انجام این کار، بازه زمانی را بسیار کوچک و را به نزدیک میکنیم. توجه به این نکته مهم است که واحد اندازهگیری سرعت و شتاب، به ترتیب برابر متر بر ثانیه () و متر بر مجذور ثانیه () است. با مرتب کردن رابطه شتاب، به رابطه مرتبتری میرسیم:
همانند سرعت متوسط و لحظهای، شتاب متوسط و لحظهای را نیز میتوان از روی نمودار سرعت-زمان بهدست آورد. برای محاسبه شتاب متوسط از روی نمودار مکان-زمان، شیب خط متصلکننده دو نقطه و را بهدست میآوریم. در مقابل، برای محاسبه شتاب لحظهای، زمانهای و به یکدیگر نزدیک میشوند. بنابراین، به جای محاسبه شیب خط متصلکننده دو نقطه، شیب نمودار در نقطه دلخواه را بهدست میآوریم.
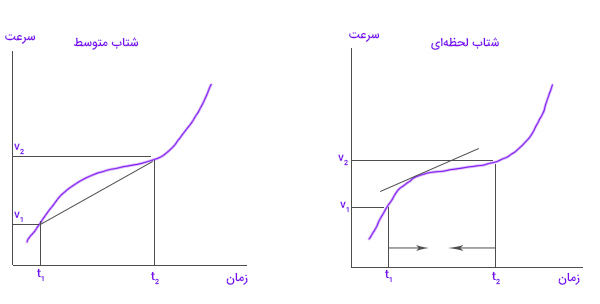
- نکته ۱: اگر شیب نمودار سرعت-زمان در هر نقطه ثابت باشد، جسم با شتاب ثابت حرکت میکند. بنابراین، شتاب متوسط و شتاب لحظهای آن با یکدیگر برابر هستند.
- نکته ۲: اگر شیب نمودار سرعت-زمان، منفی باشد، شتاب جسم با گذشت زمان، کاهش مییابد.
- نکته ۳: اگر شیب نمودار سرعت-زمان، مثبت باشد، شتاب جسم با گذشت زمان، افزایش مییابد.
- نکته ۴: اگر شتابهای متوسط و لحظهای با یکدیگر برابر باشند، حرکت جسم، حرکت با شتاب ثابت نام دارد.
پس از آشنایی با تعریف سرعت و شتاب و فرمولهای محاسبه آنها، شتاب را کمی مفهومیتر بررسی میکنیم.
مفهوم شتاب چیست ؟
شتاب یکی از نخستین ایدههای پیچیده در فیزیک است. دلیل این موضوع آن نیست که مردم هیچ شهود و درکی از شتاب ندارند. بسیاری از افراد شتاب را درک میکنند، اما در بیشتر مواقع این درک نادرست است. در حالت کلی، مفهوم یکسانی برای سرعت و شتاب در نظر گرفته میشود. شاید شما جزو آن دسته از افرادی باشید که تصور میکنند هنگامی که جسمی با سرعت زیادی در حرکت است، اندازه شتاب حرکت آن نیز باید بزرگ باشد. اما این تصور به طور کامل اشتباه است. مقدار سرعت در هر زمان، مقدار شتاب را تعین نمیکند. برای آنکه به این اطمینان برسید که اندازه سرعت، تعیینکننده شتاب نیست، پرسشهای زیر را با دقت بخوانید و سعی کنید قبل از دیدن پاسخ، به آنها جواب دهید.
مثال ۱. ماشینی با سرعتی نسبتا آرام و یکنواخت، از نزدیکی مدرسه عبور میکند.
سرعت زیاد، شتاب کم
سرعت زیاد، شتاب زیاد
سرعت کم، شتاب کم
سرعت کم، شتاب زیاد
اتومبیلی با سرعت زیاد در اتوبان، تلاش میکند از ماشین کناری سبقت بگیرد.
سرعت زیاد، شتاب کم
سرعت زیاد، شتاب زیاد
سرعت کم، شتاب کم
سرعت کم، شتاب زیاد
اتومبیلی با سرعت زیاد و تقریبا یکنواخت در اتوبان حرکت میکند.
سرعت زیاد، شتاب کم
سرعت زیاد، شتاب زیاد
سرعت کم، شتاب کم
سرعت کم، شتاب زیاد
چراغ سبز میشود و راننده اتومبیل پایش را تا ته روی گاز فشار میدهد و از چهاراه عبور میکند.
سرعت زیاد، شتاب کم
سرعت زیاد، شتاب زیاد
سرعت کم، شتاب کم
سرعت کم، شتاب زیاد
پاسخ: هنگامی که راننده پای خود را تا ته روی گاز فشار میدهد، مقدار شتاب زیاد خواهد بود، زیرا نرخ تغییر سرعت بسیار زیاد است. هنگامی که اتومبیل با سرعت نسبتا یکنواختی حرکت میکند، مقدار شتاب کم است، زیرا اندازه سرعت، تغییر زیادی نمیکند و تقریبا ثابت است. اگر اتومبیل با سرعت ثابتی حرکت کند، مقدار شتاب برابر صفر خواهد بود. هنگامی که اتومبیل با سرعت زیادی در اتوبان حرکت میکند، مقدار سرعت زیاد است. هنگامی که اتومبیل در نزدیکی مدرسه حرکت یا به هنگام سبز شدن چراغ راهنمایی-رانندگی، از چهارراه عبور میکند، مقدار سرعت آن کم خواهد بود. به این نکته دقت داشته باشید که به هنگام شروع حرکت، راننده پای خور را روی پدال گاز فشار میدهد، اما سرعت اتومبیل هنوز کم است و برای رسیدن به سرعت زیاد، زمان نیاز است. از آنجا که نرخ تغییر سرعت زیاد است، مقدار شتاب نیز زیاد خواهد بود.
تصور اشتباه دیگری نیز در مورد شتاب وجود دارد. به این جمله کمی فکر کنید، اگر شتاب منفی باشد، حرکت جسم آهسته میشود و اگر شتاب مثبت باشد، جسم سریعتر حرکت خواهد کرد. آیا این جمله صحیح است؟ خیر. جسمی با شتاب منفی میتواند سریعتر و جسمی با شتاب مثبت میتواند، آهستهتر حرکت کند. این موضوع چگونه رخ میدهد؟ به این نکته توجه داشته باشید که شتاب برداری است که جهت آن در راستای تغییر سرعت است. بنابراین، جهت شتاب تعیین میکند آیا به سرعت اضافه یا از مقدار آن کم میشود. به زبان ریاضی، معنای شتاب منفی آن است که از مقدار کنونی سرعت کاسته میشود. در مقابل، شتاب مثبت بدان معنا است که به مقدار کنونی سرعت اضافه خواهد شد. اگر مقدار اولیه سرعت منفی باشد، کم کردن مقدار سرعت سبب افزایش مقدار آن میشود. شاید با خود فکر کنید که سرعت منفیتر و مقدار آن کوچکتر میشود، اما در اینجا در مورد اندازه یا قدرمطلق سرعت صحبت میکنیم.
به عنوان مثال، گورکنی با سرعت ۳- متر بر ثانیه شروع به حرکت به سمت چپ میکند. یک متر بر ثانیه از سرعت گورکن کم میکنیم، بنابراین سرعت آن زیاد خواهد شد:
این مثال نشان میدهد کم شدن سرعت، (شتاب منفی) میتواند حرکت جسم را سریعتر کند.
اگر جهت بردارهای شتاب و سرعت یکسان باشند، جسم سریعتر حرکت خواهد کرد. اما اگر جهت این دو بردار مخالف یکدیگر باشد، حرکت جسم آهسته میشود. به تصویر نشان داده شده در ادامه دقت کنید. راننده بدون توجه به گلولای، به سمت آن حرکت میکند. به همین دلیل، حرکت اتومبیل کند میشود. سمت راست را جهت مثبت در نظر میگیریم. تا زمانی که اتومبیل به سمت راست حرکت میکند، سرعت آن مثبت و هنگامی که به سمت چپ حرکت میکند، سرعت آن منفی است. اگر سرعت حرکت اتومبیل زیاد شود، جهت شتاب در راستای جهت سرعت خواهد بود و اما اگر سرعت حرکت اتومبیل کم شود، بردارهای شتاب و سرعت در خلاف یکدیگر قرار میگیرند.
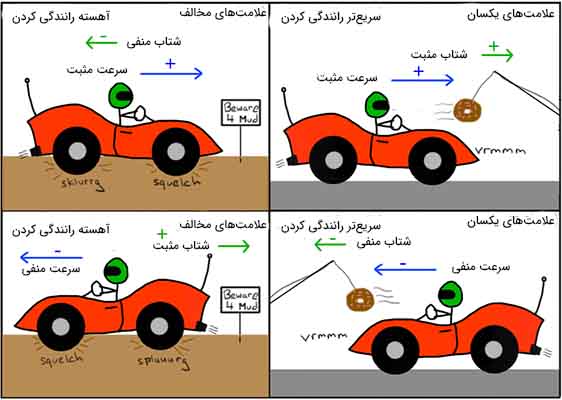
تاکنون با مفهوم شتاب، تفاوت سرعت با شتاب و فرمول شتاب و سرعت آشنا شدهایم. همچنین، گفتیم شتاب به دو نوع شتاب لحظهای و متوسط تقسیم میشود. به مقدار شتاب در بازه زمانی مشخصی، به عنوان مثال سه ثانیه اول حرکت، شتاب متوسط گفته میشود. به اندازه شتاب حرکت جسم در هر لحظه از زمان، شتاب لحظهای میگوییم. در ادامه، با فرمولهای کلیتر این دو شتاب با ذکر مثالهای مختلف آشنا میشویم.
فرمول شتاب متوسط و شتاب لحظه ای چیست ؟
شتاب را به صورت نرخ تغییرات سرعت تعریف کردیم. اگر تغییرات سرعت مثبت باشد (سرعت افزایش یابد)، شتاب مثبت خواهد بود. در مقابل، اگر تغییرات سرعت منفی باشد (سرعت کاهش یابد)، شتاب منفی میشود. همچنین، اگر تغییرات سرعت برابر صفر باشد (حرکت با سرعت ثابت)، مقدار شتاب برابر صفر است. سوالی که ممکن است مطرح شود آن است که اگر جهت حرکت جسم تغییر کند، آیا شتاب به وجود میآید یا مقدار شتاب اولیه تغییر میکند. به بیان دیگر، اگر جهت حرکت جسمی با سرعت ثابت تغییر کند، چه چیزی در مورد حرکت آن میتوان گفت؟ این نکته را به یاد داشته باشید، اگر اندازه سرعت حرکت جسمی تغییر کند، حرکت جسم شتابدار خواهد بود. اگر جهت حرکت جسمی با سرعت ثابت تغییر کند، جسم شتابی به نام شتاب مرکزگرا بهدست میآورد. در مورد شتاب مرکزگرا در ادامه صحبت میکنیم.
نکته: سرعت کمیتی برداری با اندازه و جهت است. بنابراین، هنگامی که اندازه سرعت، جهت آن یا هر دو تغییر کنند، جسم شتاب بهدست میآورد.
شتاب متوسط با استفاده از فرمول زیر بهدست می آید:
شتاب لحظهای نیز با استفاده از رابطه زیر محاسبه میشود:
مقدار در شتاب لحظهای بسیار کوچک و به صفر نزدیک میشود. گاهی از رابطه مربوط به شتاب متوسط برای تخمین شتاب لحظهای استفاده میکنیم. اگر فرمول شتاب متوسط را مرتب کنیم، به صورت زیر نوشته خواهد شد:
رابطه فوق نشان میدهد که با داشتن سرعتهای اولیه و نهایی و مدت زمان تغییرات آنها، شتاب متوسط را میتوان بهدست آورد. شتاب متوسط با استفاده از فرمول زیر نیز محاسبه میشود:
رابطه فوق را بر حسب شتاب متوسط مرتب میکنیم:
در نتیجه، شتاب متوسط با استفاده از دو فرمولی که در بالا گفته شد، بهدست می آید.
پرسش: نمودار سرعت حرکت جسمی برحسب زمان به صورت زیر داده شده است. در فاصله زمانی تا ، شتاب متوسط و لحظهای را روی نمودار نشان دهید.
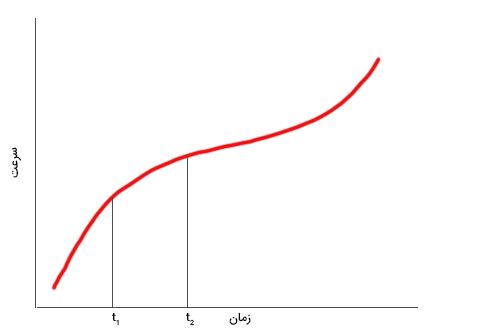
پاسخ: در مطالب بالا، در مورد شتابهای لحظهای و متوسط و چگونگی نمایش آنها روی نمودار سرعت-زمان صحبت کردیم. برای بهدست آوردن شتاب متوسط روی نمودار سرعت-زمان، نقطه شروع و پایان حرکت را به یکدیگر متصل و شیب خط را بهدست میآوریم.
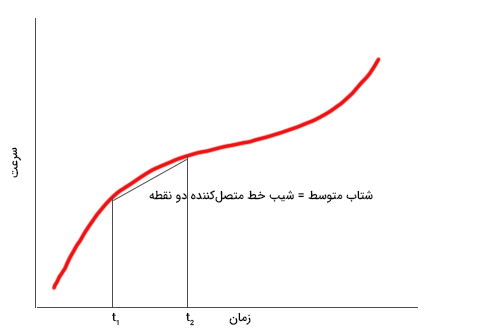
در شتاب لحظهای، زمانهای تا به یکدیگر نزدیک میشوند. به بیان دیگر، به سمت صفر میل میکند. از اینرو، شتاب لحظهای برابر شیب خط مماس بر نمودار سرعت-زمان در لحظه زمانی t است.
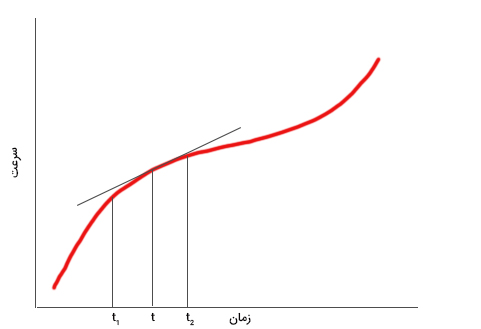
به هنگام صحبت در مورد شیب نمودار، چه چیزی را به یاد میآورید؟ مشتق. در نتیجه، برای محاسبه شتاب لحظهای، کافی است از سرعت بر حسب زمان، مشتق بگیرید.
مثال اول محاسبه شتاب متوسط
سرعت اتومبیلی در مدت زمان ۴ ثانیه، از ۱۰ متر بر ثانیه به ۳۰ متر بر ثانیه تغییر میکند. شتاب متوسط آن را بهدست آورید.
پاسخ
دادههای مسئله عبارت هستند از:
شتاب متوسط با استفاده از رابطه زیر بهدست میآید:
دادههای مسئله را در رابطه بالا قرار میدهیم:
مثال دوم محاسبه شتاب متوسط
سرعت اتوبوسی پس از طی مسافت ۴۰۰ متر، از ۱۵ متر بر ثانیه به ۴۵ متر بر ثانیه افزایش مییابد. مقدار شتاب متوسط آن را بهدست آورید.
پاسخ
دادههای مسئله عبارت هستند از:
فرمول دیگری که برای محاسبه شتاب متوسط میتوان از آن استفاده کرد، عبارت است از:
با قرار دادن، دادههای مسئله در رابطه بالا، داریم:
نکته: هنگامی که سرعت اولیه، سرعت نهایی و زمان بین تغییر سرعت داده شوند، برای محاسبه شتاب متوسط از فرمول زیر استفاده میکنیم:
هنگامی که سرعت اولیه، سرعت نهایی و مسافت طی شده توسط جسم داده شوند، از رابطه زیر برای محاسبه شتاب متوسط استفاده میکنیم:
عقابی با سرعت ۳۴ متر بر ثانیه به سمت چپ حرکت میکند. باد در خلاف جهت حرکت عقاب شروع به وزیدن میکند و منجر به کاهش حرکت آن با شتاب ثابت ۸ متر بر مجذور ثانیه میشود. بزرگی سرعت حرکت عقاب را ۳ ثانیه پس از وزش باد بهدست آورید.
در این مثال، مقدار شتاب، سرعت اولیه و زمان تغییر سرعت داده شده است و باید بزرگی سرعت را پس از ۳ ثانیه از شروع وزش باد بهدست آوریم. از آنجا که مسافت طی شده توسط عقاب داده نشده است، از فرمول زیر برای محاسبه شتاب متوسط استفاده میکنیم:
رابطه بالا را برحسب مینویسیم:
با قرار دادن سرعت اولیه در رابطه بالا، داریم:
چرا علامت سرعت را منفی قرار دادیم؟ زیرا، حرکت به سمت راست را به طور اختیاری، جهت مثبت گرفتهایم. در ادامه، شتاب و مدت زمان تغییر سرعت را در رابطه قرار میدهیم. به این نکته توجه داشته باشید که علامت شتاب مخالف علامت سرعت و مثبت است، زیرا حرکت عقاب کند میشود:
بنابراین، بزرگی سرعت برابر خواهد بود.
مثال اول محاسبه شتاب لحظه ای
سرعت لحظهای ذرهای با استفاده از تابع زیر توصیف میشود:
- شتاب متوسط ذره را بین ۲ تا ۴ ثانیه بهدست آورید.
- شتاب لحظهای ذره را در زمان بهدست آورید.
پاسخ
قسمت ۱: فرمول شتاب متوسط را به صورت زیر مینویسیم:
برای بهدست آوردن شتاب متوسط ذره، باید مقدار سرعت حرکت آن را در ثانیههای ۴ و ۲ بهدست آوریم. برای انجام این کار، زمان را در رابطه سرعت قرار میدهیم.
مقدار سرعت در زمان ۲ ثانیه:
مقدار سرعت در زمان ۴ ثانیه:
با قرار دادن مقدار سرعت در زمانهای ۲ و ۴ ثانیه در رابطه شتاب متوسط داریم:
قسمت ۲: شتاب لحظهای را به صورت زیر تعریف کردیم:
را باید به گونهای کوچک کنیم که به ۳ ثانیه نزدیک باشد. بنابراین، تغییرات زمانی در نزدیکی ثانیه سوم، صفر یا بسیار نزدیک به صفر خواهد بود. برای محاسبه شتاب لحظهای در زمان ۳ ثانیه، ابتدا بازه زمانی را انتخاب میکنیم و در رابطه داده شده برای سرعت برحسب زمان قرار میدهیم.
بازه زمانی را کوچکتر و برابر انتخاب میکنیم.
هرچه بازه زمانی را کوچکتر کنیم، شتاب متوسط به شتاب لحظهای نزدیکتر خواهد شد. برای بهدست آوردن جواب دقیق، از تابع سرعت برحسب زمان، مشتق میگیریم.
در نتیجه، مقدار شتاب لحظهای در زمان ۳ ثانیه برابر است با:
در مطالب بالا، اندکی در مورد نمودار سرعت برحسب زمان صحبت کردیم و چگونگی محاسبه شتاب متوسط و لحظهای را به طور خلاصه توضیح دادیم. در ادامه، در مورد چگونگی محاسبه شتاب از روی نمودار سرعت-زمان با جزییات بیشتری صحبت خواهیم کرد.
محاسبه شتاب لحظه ای و متوسط از روی نمودار سرعت برحسب زمان
نمودار سرعت-زمان زیر را در نظر بگیرید. مقدار سرعت در زمان ۴ ثانیه، چه مقدار است؟ برای پاسخ به این پرسش، ابتدا زمان ۴ ثانیه را روی محور افقی (زمان) مشخص و از نقطه خطی موازی محور عمودی (سرعت)، رسم میکنیم. محل تقاطع خط عمودی و نمودار سرعت-زمان با ستاره مشخص شده است. از محل تقاطع، خطی موازی محور افقی (زمان) رسم میکنیم تا محور عمودی یا سرعت را قطع کند. محل تقاطع، سرعت در زمان ۴ ثانیه، یعنی ۳ متر بر ثانیه، را به ما میدهد.
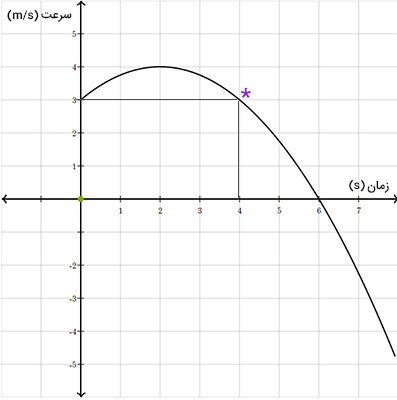
شیب نمودار سرعت-زمان، نشاندهنده شتاب حرکت جسم است. بنابراین، شیب نمودار در زمانی مشخص، بیانگر شتاب حرکت در آن لحظه است. هنگامی که شیب نمودار سرعت-زمان زیاد باشد، تغییرات سرعت حرکت بسیار سریع خواهد بود. هنگامی که شیب نمودار ملایم باشد، سرعت حرکت جسم به آرامی تغییر میکند. همچنین، اگر شیب نمودار سرعت-زمان منفی باشد، شتاب منفی و اگر شیب نمودار مثبت باشد، مقدار شتاب نیز مثبت خواهد بود.
به نمودار زیر دقت کنید و به پرسشهای زیر پاسخ دهید.
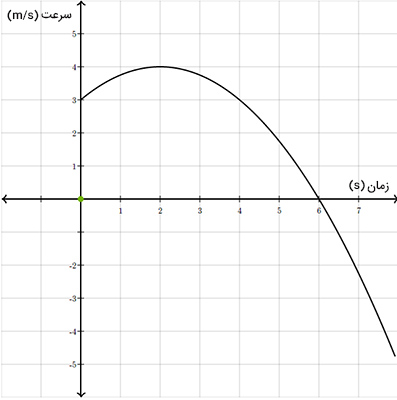
پرسش ۱: شیب نمودار در چه بازه زمانی مثبت است؟
پاسخ: شیب نمودار در بازه زمانی صفر تا ۲ ثانیه مثبت است، بنابراین جسم در این بازه زمانی با شتاب مثبت حرکت میکند.
پرسش ۲: شیب نمودار در چه بازه زمانی منفی است؟
پاسخ: شیب نمودار در بازه زمانی ۲ تا ۸ ثانیه منفی است، بنابراین جسم در این بازه زمانی با شتاب منفی حرکت میکند. خط مماس بر نمودار در زمان ۲ ثانیه، موازی محور افقی است. از اینرو، شیب آن برابر صفر خواهد بود. بنابراین، شتاب حرکت جسم در این لحظه برابر صفر است. حرکت با شتاب صفر به چه معنا است؟ اگر شتاب حرکت جسمی برابر صفر باشد، دو نتیجه میتوان گرفت:
- جسم با سرعت ثابت حرکت میکند.
- سرعت حرکت جسم پس از افزایش (کاهش)، کاهش (افزایش) مییابد.
پرسش ۳: حرکت جسمی به صورت نمودار نشان داده شده در تصویر زیر، توصیف میشود. در زمان ۴ ثانیه، حرکت جسم سریعتر میشود یا آهستهتر؟

پاسخ: جسم در زمان ، آهستهتر حرکت میکند. دو توضیح برای این پاسخ وجود دارد:
توضیح اول
شیب نمودار در منفی و در نتیجه، شتاب آن نیز منفی است. اما جسم در این زمان با سرعت حرکت میکند. از آنجا که علامتها سرعت و شتاب مخالف یکدیگر هستند، حرکت جسم باید آهستهتر شود.
توضیح دوم
در زمان ، نمودار سرعت-زمان به محور افقی نزدیک میشود. از آنجا که محور افقی نشاندهنده سرعت صفر است، حرکت جسم کندتر خواهد شد. به طور مشابه، دور شدن نمودار سرعت-زمان از محور افقی، نشاندهنده حرکت سریعتر جسم است. نمودار سرعت-زمان، محور افقی را در زمان ۶ ثانیه قطع میکند. بنابراین، در این زمان، سرعت حرکت جسم صفر میشود. از ثانیه ششم به بعد، نمودار از محور افقی دور و حرکت جسم سریعتر میشود.
مثال محاسبه شتاب متوسط و لحظه ای از روی نمودار سرعت-زمان
حرکت جسمی با استفاده از نمودار سرعت-زمان، به صورت زیر نشان داده شده است.
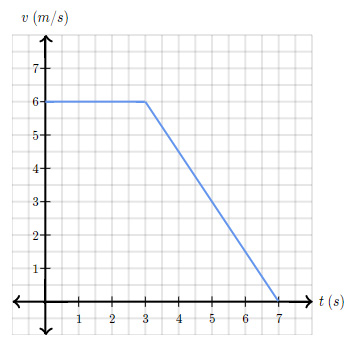
- مقدار شتاب را در زمان ۴ ثانیه بهدست آورید.
- مقدار شتاب را در بازه زمانی ۳ تا ۷ ثانیه بهدست آورید.
قسمت ۱: از آنجا که مقدار شتاب در یک زمان مشخص خواسته شده است، شتاب در آن لحظه برابر شتاب لحظهای خواهد بود. برای بهدست آوردن شتاب لحظهای در زمان مشخص t، شیب نمودار را در آن لحظه بهدست میآوریم. نمودار سرعت-زمان در لحظه به شکل خطی با شیب ثابت و منفی است. در نتیجه، برای محاسبه شتاب در زمان ، کافی است شیب خط را محاسبه کنیم. برای محاسبه شیب خط به معادله خط یا دو نقطهای که خط از آنها میگذرد، نیاز داریم. در اینجا، معادله خط را نداریم، بنابراین از دو نقطه ابتدا و انتهای خط برای محاسبه شیب استفاده میکنیم.
نقطه ابتدا:
نقطه ابتدا:
بنابراین، شیب خط و شتاب در زمان ۴ ثانیه برابر، خواهد بود.
قسمت ۲: در این قسمت، شتاب را در بازه زمانی خواسته شده باید بهدست آوریم. از آنجا که شتاب در بازه زمانی و نه در یک زمان محاسبه میشود، شتاب بهدست آمده، همان شتاب متوسط حرکت جسم است.
نکته: هنگامی که شیب نمودار سرعت-زمان ثابت باشد، مقدار شتاب متوسط و لحظهای برابر خواهند بود.
با توجه به نکته گفته شده در بالا، شتاب متوسط در بازه زمانی ۳ تا ۷ ثانیه برابر شتاب لحظهای محاسبه شده در قسمت یک است. از اینرو، شتاب متوسط نیز برابر بهدست میآید.
فرمول شتاب با نیرو چیست ؟
شتاب با نیرو نسبت مستقیم دارد و جهت آنها با یکدیگر یکسان است. تا اینجا گفتیم، شتاب متوسط و لحظهای را میتوانیم با داشتن سرعتهای اولیه و نهایی جسم و مدت زمان تغییر سرعت، بهدست آوریم. در ادامه، با بیان قانون دوم نیوتن، فرمول دیگری را برای محاسبه شتاب، توضیح میدهیم. قبل از بیان قانون دوم نیوتن، کمی در مورد نیرو و اثر آن روی حرکت جسم صحبت خواهیم کرد.
فرض کنید توپی با سرعت ثابت، حرکت میکند. تا وقتی ضربه یا نیرویی به توپ وارد نشود، حرکت آن تغییر نخواهد کرد. به بیان دیگر، تا هنگامی که نیرویی بر توپ وارد نشود، توپ به حرکت خود با سرعت ثابت ادامه میدهد. هنگامی که به توپ ضربهای وارد کنیم، با سرعت بیشتری به حرکت خود ادامه خواهد داد. بنابراین، سرعت توپ افزایش مییابد و حرکت آن شتابدار میشود. در نتیجه، وارد کردن نیرو بر جسم سبب ایجاد شتاب در حرکت آن خواهد شد. هرچه مقدار نیروی وارد شده بیشتر باشد، مقدار شتاب حرکت نیز بیشتر میشود.
بر طبق قانون دوم نیوتن، شتاب حرکت جسم به طور مستقیم با مجموع نیروی وارد شده بر آن و به طور معکوس با جرم جسم، متناسب است.
با توجه به رابطه بالا، اگر مجموع نیروهای وارد شده بر جسمی افزایش یابد، جسم با شتاب بیشتری حرکت خواهد کرد. همچنین، اگر مجموع نیروهای وارد شده ثابت بماند و جرم جسم افزایش یابد، شتاب حرکت کاهش خواهد یافت.
مثال اول فرمول شتاب و نیرو
جسمی به جرم ۵ کیلوگرم روی سطح بدون اصطکاکی قرار دارد. اگر نیرویی برابر ۴۰ نیوتن به سمت راست بر جسم وارد شود، شتاب حرکت و جهت شتاب را بهدست آورید.

پاسخ: نیروی وارد شده بر جسم و شتاب حرکت آن با استفاده از رابطه زیر به یکدیگر مربوط میشوند:
با جایگذاری مقدارهای داده شده در مثال در رابطه فوق، داریم:
جهت شتاب و نیرو یکسان و هر دو به سمت راست هستند.
مثال دوم فرمول شتاب و نیرو
جسمی به جرم ۸ کیلوگرم روی میزی قرار دارد. اگر نیرویی برابر ۳۵ نیوتن به سمت چپ بر جسم وارد شود و نیروی اصطکاک وارد شده بر جسم از سمت میز، برابر ۱۹ نیوتن باشد، شتاب حرکت و جهت شتاب را بهدست آورید.
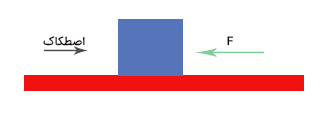
پاسخ: سمت راست را راستای مثبت در نظر میگیریم. برای بهدست آوردن شتاب حرکت جسم، ابتدا برآیند نیروهای وارد شده بر آن را محاسبه میکنیم. دو نیرو بر جسم وارد میشوند:
- نیروی F به سمت چپ.
- نیروی اصطکاک به سمت راست.
منفی بودن نیروی برآیند نشان میدهد که راستای آن به سمت چپ است. بنابراین، شتاب جسم نیز به سمت چپ خواهد بود. اندازه شتاب حرکت برابر است با:
جسمی را در نظر بگیرید که با سرعت به سمت راست حرکت میکند. بنابراین سرعت آن مثبت است. اگر جهت نیروی کل وارد شده بر جسم نیز به سمت راست باشد، حرکت آن چگونه خواهد بود؟ اگر جهت نیروی کل و سرعت حرکت جسم با یکدیگر یکسان باشند، سرعت حرکت افزایش مییابد. بنابراین، جسم شتاب میگیرد. اکنون حالتی را در نظر بگیرید که جسم به سمت راست حرکت میکند، اما نیروی F به سمت چپ بر آن وارد میشود. چه اتفاقی میافتد؟ اگر سرعت و نیرو در خلاف جهت یکدیگر باشند، سرعت حرکت جسم کاهش مییابد. بنابراین، حرکت جسم کند خواهد شد.
اگر جسم به سمت راست حرکت کند و نیروی وارد شده بر آن عمود بر سرعت و به سمت بالا بر آن وارد شود، چه اتفاقی رخ خواهد داد؟ هرگاه نیرو و سرعت بر یکدیگر عمود باشند، سرعت حرکت جسم تغییری نخواهد کرد. در این حالت، جهت حرکت تغییر میکند.
مثال سوم فرمول شتاب و نیرو
مقدار متوسط نیروی لازم برای تغییر سرعت جعبهای به جرم ۵ کیلوگرم از صفر به ۵۴ متر بر ثانیه در مدت زمان ۹ ثانیه، چه مقدار است؟
پاسخ
برای بهدست آوردن نیروی متوسط وارد بر جسم، باید شتاب حرکت آن را بهدست آوریم. در این مثال، سرعتهای اولیه، نهایی و مدت زمان تغییر سرعت داده شدهاند، بنابراین از فرمول شتاب متوسط استفاده میکنیم:
جسم از حال سکون شروع به حرکت میکند، بنابراین مقدار زمان و سرعت اولیه برابر صفر است:
فرمول شتاب برحسب نیرو به صورت زیر نوشته میشود:
مثال چهارم فرمول شتاب و نیرو
اتومبیلی به جرم 1500 کیلوگرم با سرعت ۲۰/۱ کیلومتر بر ساعت حرکت میکند. این اتومبیل پس از طی مسافت ۲۰۰ متر، متوقف میشود. نیروی متوسط وارد شده از طرف ترمزها بر آن چه مقدار است؟
پاسخ
اگر فرض کنیم اتومبیل با سرعت ۲۰/۱ کیلومتر بر ساعت به سمت راست حرکت میکند، پس از ترمز، نیرویی در خلاف جهت حرکت (سمت چپ) بر آن وارد خواهد شد. به این نکته توجه داشته باشید که حرکت اتومبیل آهسته میشود، بنابراین نیرو و شتاب در خلاف جهت یکدیگر هستند. برای بهدست آوردن نیروی متوسط وارد شده بر اتومبیل، شتاب حرکت آن را بهدست میآوریم. با توجه به آنکه سرعت اولیه، نهایی و مسافت طی شده داده شدهاند، از رابطه زیر برای بهدست آوردن شتاب متوسط استفاده میکنیم:
مقدار منفی بهدست آمده برای شتاب، آهسته شدن حرکت اتومبیل را نشان میدهد. با داشتن مقدار شتاب، نیروی متوسط را بهدست میآوریم:
فرمول شتاب گرانش چیست ؟
تا اینجا، با فرمول شتاب لحظهای، شتاب متوسط، و فرمول شتاب با نیرو آشنا شدیم. در این بخش، در مورد فرمول شتاب گرانش صحبت خواهیم کرد. فرض کنید جسمی در ارتفاع مشخصی از سطح ماه قرار دارد. ماه، جسم را به سمت خود میکشاند، بنابراین جسم شتاب میگیرد. برای درک بهتر این حالت به مثال سیب و زمین توجه کنید. اگر سیب را از ارتفاع مشخصی از سطح زمین رها کنید، زمین آن را به سمت خود میکشاند. حالت مشابهی در ماه رخ میدهد. ماه بر جسمی که در نزدیکی آن قرار دارد، نیروی گرانشی وارد میکند. در بخش قبل گفتیم، هرگاه نیرویی بر جسمی وارد شود، جسم شتابی در راستای نیروی وارد شده بر آن بهدست میآورد. به این شتاب، شتاب حاصل از نیروی گرانش یا شتاب گرانشی گفته میشود.
برای بهدست آوردن فرمول شتاب گرانشی، ابتدا رابطه بین نیروی کل وارد بر جسم و شتاب را مینویسیم. اگر نیروی کل در راستای x باشد، داریم:
نیروی گرانش با استفاده از رابطه زیر بهدست میآید:
در رابطه فوق:
- و جرم دو جسم هستند.
- G ثابت گرانش جهانی است.
- r فاصله بین دو جسم است.
اگر یکی از دو جسم، ماه و دیگری جسم دلخواهی به جرم M باشد، به صورت زیر نوشته خواهد شد:
در این حالت، R فاصله بین مرکز ماه تا جسم است. در ادامه، را برابر قرار میدهیم.
با ساده کردن m از طرفین رابطه بالا، داریم:
همان شتاب جاذبه گرانشی است و به طور معمول با g نشان داده میشود.
بنابراین، شتاب جاذبه حاصل از گرانش در سطح هر سیاره دلخواهی، با جرم سیاره نسبت مستقیم و با فاصله جسم تا مرکز سیاره، نسبت معکوس دارد.
مثال اول فرمول شتاب گرانش
شتاب حاصل از نیروی جاذبه ماه (گرانش) را بهدست آورید. جرم ماه برابر و شعاع آن برابر است.
پاسخ
شتاب جاذبه گرانشی در سطح ماه با استفاده از رابطه زیر بهدست میآید:
مقدار ثابت جهانی گرانش برابر است. با قرار دادن G و جرم و شعاع ماه در رابطه بالا، داریم:
توجه به این نکته مهم است که برای بهدست آوردن شتاب جاذبه گرانش در سطح ماه، فرض میکنیم جسم روی آن قرار دارد. بنابراین، r برابر شعاع ماه خواهد بود.
مثال دوم فرمول شتاب گرانش
شتاب جاذبه گرانشی را
- در سطح زمین بهدست آورید.
- در فاصله ۳۵۰۰ کیلومتری از سطح زمین، محاسبه کنید.
جرم زمین برابر و شعاع آن برابر است.
پاسخ
قسمت اول: ابتدا شتاب جاذبه گرانشی را در سطح زمین بهدست میآوریم.
قسمت دوم: اکنون جسم در فاصله ۳۵۰۰ کیلومتری از سطح زمین قرار دارد. قبل از حل این قسمت، به این پرسش فکر کنید، آیا مقدار شتاب جاذبه گرانش افزایش مییابد یا کاهش؟ از آنجا که g با فاصله به صورت معکوس تغییر میکند، مقدار آن کاهش خواهد یافت.
شتاب جاذبه گرانشی سیاره X برابر است. اگر جرم این سیاره برابر کیلوگرم باشد، جرم آن را بهدست آورید.
کیلوگرم
کیلوگرم
کیلوگرم
کیلوگرم
دادههای پرسش عبارت هستند از:
فرمول شتاب جاذبه گرانشی برابر است با:
رابطه بالا را برحسب M مرتب میکنیم:
مقدارهای داده شده را در رابطه فوق قرار میدهیم:
فرمول شتاب مرکزگرا چیست ؟
تاکنون با فرمول شتاب متوسط، لحظهای، رابطه بین شتاب و نیرو (قانون دوم نیوتن) و شتاب جاذبه گرانشی آشنا شدیم. در این بخش، شتاب مرکزگرا و فرمول آن را توضیح خواهیم داد.
جسمی را در نظر بگیرید که در مسیر دایرهای به صورت نشان داده شده در تصویر حرکت میکند. بردار سرعت حرکت جسم در نقاط مختلف در امتداد مسیر حرکت آن، نشان داده شده است. در این بخش، فرض میکنیم بزرگی سرعت در تمام نقاط یکسان است. به عبارت دیگر، جهت بردار سرعت در هر لحظه تغییر میکند، اما مقدار آن ثابت است. همچنین، شعاع مسیر دایرهای را برابر r در نظر میگیریم. بنابراین، مکان بردار سرعت در هر لحظه ثابت و برابر r خواهد بود.
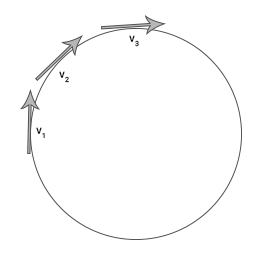
در ادامه، فرمول شتاب مرکزگرا را بهدست میآوریم. سرعتهای نشان داده شده در تصویر را در دایرهای دیگری و از مرکز آن رسم میکنیم. در این حالت، شعاع دایره برابر v خواهد بود.
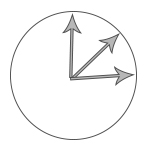
میدانیم بردار سرعت، تغییرات مکان برحسب زمان را به ما میدهد. سوالی که ممکن است مطرح شود آن است که چه عاملی سبب تغییرات بردار سرعت برحسب زمان میشود. پاسخ این پرسش، بردار شتاب است.
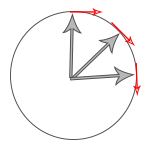
بردارهای قرمز نشان داده شده در تصویر بالا، بردارهای شتاب هستند. در دایره اول، بردار مکان همانند عقربه ساعت میچرخد و عامل این چرخش، بردار سرعت است. در دایره سوم، بردار سرعت همانند عقربه ساعت میچرخد و عامل حرکت آن، بردارهای شتاب هستند. همچنین، در دایره اول، بردارهای سرعت بر مسیر دایرهای مماس و بر بردار مکان عمود هستند. در دایره سوم، بردار شتاب بر مسیر حرکت دایرهای مماس و بر بردار سرعت عمود است. چرا این شتاب، شتاب مرکزگرا نامیده میشود؟ اگر بردارهای قرمز نشان داده شده در دایره سوم را به دایره اول اضافه کنیم، به شکل زیر خواهیم رسید.
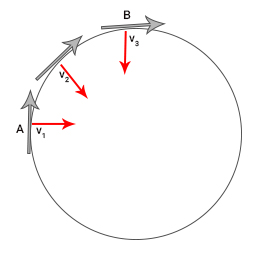
همانند بردار سرعت، بزرگی بردار شتاب را در تمام مسیر دایرهای یکسان و برابر در نظر میگیریم. در ادامه، مدت زمان لازم برای حرکت از نقطه A به نقطه B را بهدست میآوریم. برای انجام این کار، طول کمان AB را حساب میکنیم. با توجه به تصویر، کمان AB برابر یکچهارم محیط دایره است:
زمان لازم برای طی کردن کمان AB، برابر طول کمان تقسیم بر بزرگی سرعت حرکت ذره روی کمان است:
توجه به این نکته مهم است که مدت زمان لازم برای رفتن از نقطه A به B روی دایرهای به شعاع r برابر مدت زمان لازم برای رفتن از نقطه A به B روی دایره نشان داده شده در تصویر زیر به شعاع است.
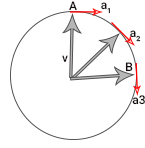
برای مدت زمان لازم برای رفتن از نقطه A به B در دایره بالا، ابتدا طول کمان AB را بهدست میآوریم. طول این کمان نیز، برابر یکچهارم محیط دایره است. در اینجا به این نکته توجه داشته باشید که شعاع دایره برابر ، بزرگی سرعت حرکت، خواهد بود. چه کمیتی در امتداد دایره حرکت میکند؟ در این حالت، بردار مماس بر دایره به جای بردار شتاب است و در امتداد آن حرکت میکند. از اینرو، در مخرج به جای ، کمیت a را قرار میدهیم:
دو رابطه بهدست آمده برای زمان را برابر یکدیگر قرار میدهیم:
پس از ساده کردن تساوی فوق به فرمول شتاب مرکزگرا میرسیم:
مثال اول فرمول شتاب مرکزگرا
توپی به انتهای نخی افقی بسته شده است و در مسیر دایرهای به شعاع ۱/۵ متر حرکت میکند. توپ در هر ثانیه دو بار به طور کامل میچرخد. مقدار شتاب مرکزگرا را بهدست آورید.
پاسخ: فرمول شتاب مرکزگرا را به صورت زیر بهدست آوردیم:
در این مثال، شعاع دایره برابر طول نخ، ۱/۵ متر، است. بنابراین، برای بهدست آوردن مقدار شتاب مرکزگرا، تنها باید سرعت حرکت را بهدست آوریم. توپ بسته شده به نخ در هر ثانیه، دو دور کامل مسیر دایرهای به شعاع ۱/۵ متر را طی میکند. طول هر چرخش برابر محیط دایره است:
سرعت حرکت از حاصلضرب طول هر چرخش در فرکانس بهدست میآید. از آنجا که در هر ثانیه، توپ دو بار به طور کامل میچرخد، فرکانس برابر دو خواهد بود:
با داشتن سرعت و شعاع دایره، شتاب مرکزگرا را بهدست میآوریم:
مثال دوم فرمول شتاب مرکزگرا
اگر شهربازی رفته باشید، به احتمال قوی سوار محفظهای به نام استوانه جادویی شدهاید. پس از ورود به محفظه استوانهای و تکیه به دیوار، استوانه شروع به چرخش میکند. هنگامی که سرعت چرخش آن به مقدار مشخصی رسید، کف استوانه باز و زیر پای شما خالی میشود، اما هیچ اتفاقی برای شما نخواهد افتاد، چرا؟ شتاب و نیروی مرکزگرا نقش مهمی در اینجا ایفا میکند.
دانشآموزی به جرم ۵۰ کیلوگرم تصمیم میگیرد سوار استوانه جادویی شود. ضریب اصطکاک ایستایی بین دانشآموز و دیوار استوانه برابر ۰/۸ است. اگر شعاع استوانه برابر ۱۰ متر باشد، حداکثر دوره تناوب چرخش استوانه برای نگه داشتن دانشآموز پس از باز شدن کف آن را بهدست آورید. شتاب جاذبه گرانشی زمین را 10 متر بر مجذور ثانیه در نظر بگیرید.
پاسخ
برای حل این مثال، گامهای زیر را طی خواهیم کرد:
گام اول
در ابتدا، مقدار کمینه نیروی اصطکاک ایستایی را بهدست میآوریم. دو نیرو بر دانشآموز وارد میشوند:
- نیروی وزن به سمت پایین
- نیروی اصطکاک ایستایی به سمت بالا
از آنجا که دانشآموز در مکان خود ساکن باقی میماند و پس از باز شدن کف محفظه، سقوط نمیکند، نیروهای وزن و اصطکاک ایستایی باید با یکدیگر برابر باشند:
گام دوم
پس از بهدست آوردن مقدار کمینه نیروی اصطکاک ایستایی، نیروی عمودی لازم برای این مقدار نیروی اصطکاک را محاسبه میکنیم:
گام سوم
مقدار بهدست آمده برای نیروی عمودی سطح برابر مقدار کمینه نیروی مرکزگرا برای نگهداشتن دانشآموز پس از باز شدن کف محفظه استوانهای است.
گام چهارم
با استفاده از رابطه زیر، شتاب مرکزگرا را به سرعت انتقالی، تبدیل میکنیم:
گام پنجم
سرعت بهدست آمده در گام چهارم، برابر سرعتی چرخش محفظه استوانهای است. در ادامه، بیشینه دوره تناوب چرخش استوانه را بهدست میآوریم.
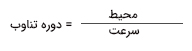
در صورتی که نمیدانید چگونه به رابطه بالا برسید، از تحلیل ابعادی (واحدها) استفاده کنید.
مثال سوم فرمول شتاب مرکزگرا
کودکی به جرم ۲۵ کیلوگرم سوار چرخوفلکی به شعاع ۵ متر شده است. اگر سرعت حرکت کودک برابر ۶ متر بر ثانیه باشد، مقدار نیروی مرکزگرا را بهدست آورید.
پاسخ
در مطالب بالا گفتیم نیروی وارد بر جسمی دلخواه با شتاب حرکت آن به طور مستقیم متناسب است:
a برابر شتاب مرکزگرا است و با استفاده از رابطه زیر بهدست میآید:
با ترکیب دو رابطه، نیروی مرکزگرا با استفاده از رابطه زیر بهدست میآید:
مثال چهارم فرمول شتاب مرکزگرا
در مدل کلاسیک اتم، الکترون در مسیر دایرهای به دور هسته میچرخد. اگر قطر تقریبی اتم برابر باشد و الکترون با سرعت ۲۲۰۰ کیلومتر بر ثانیه به دور هسته در مسیر دایرهای حرکت کند، نیروی مرکزگرای وارد شده از طرف هسته بر الکترون را بهدست آورید. جرم الکترون را برابر در نظر بگیرید.
پاسخ
نیروی مرکزگرا با استفاده از رابطه زیر بهدست میآید:
مقدارهای داده شده در مثال را در رابطه بالا قرار میدهیم. به این نکته توجه داشته باشید که در مثال، قطر اتم داده شده است و ما باید شعاع اتم را در فرمول شتاب مرکزگرا قرار دهیم:
توپی به جرم یک کیلوگرم به طنابی به طول ۲ متر بسته شده است. اگر این توپ در مسیر دایرهای عمودی با سرعت ثابت و دوره تناوب ۲ ثانیه بچرخد، بیشینه نیروی کشش طناب برابر است با:
۲۷/۹ نیوتن
۱۹/۷ نیوتن
۲۵/۶ نیوتن
۱۷/۷ نیوتن
توپ به شکل زیر در مسیر دایرهای حرکت میکند و دو نیروی کشش و گرانش (نیروی وزن) بر آن وارد میشوند. در ابتدا باید نقطهای را بیابیم که مقدار نیروی کشش در آن نقطه بیشینه است. در بالاترین نقطه، نیروهای وزن و کشش در راستای یکدیگر و به پایین و در پایینترین نقطه، این دو نیرو در خلاف جهت یکدیگر هستند.
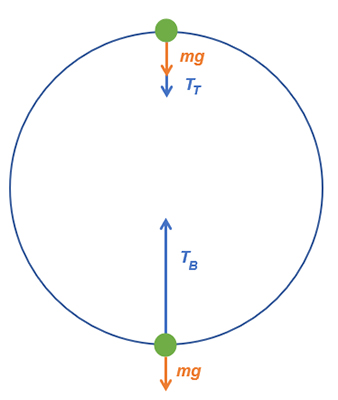
از آنجا که توپ در مسیر دایرهای و با شتاب مرکزگرای حرکت میکند، برآیند نیروهای وارد بر آن در هر نقطه برابر است. برآیند نیروها را برای بالاترین و پایینترین نقطه مینویسیم.
برآیند نیروها در پایینترین نقطه:
برآیند نیروها در بالاترین نقطه:
به این نکته توجه داشته باشید که همان نیروی مرکزگرا است و با نشان داده میشود.
مقدار نیروی کشش در پایینترین نقطه:
مقدار نیروی کشش در بالاترین نقطه:
بنابراین نیروی کشش در پایینترین نقطه، بیشینه است:
مقدار g را میدانیم، اما مقدار را باید بهدست آوریم:
شعاع مسیر دایرهای را میدانیم، بنابراین باید مقدار سرعت را به صورت زیر بهدست میآوریم:
در رابطه فوق، P دوره تناوب و برابر ۲ ثانیه است. با قرار دادن سرعت در فرمول شتاب مرکزگرا، داریم:
را در رابطه نیروی کشش در پایینترین نقطه قرار میدهیم:
حل مسئله در فرمول شتاب
تا اینجا، با فرمول شتاب لحظهای، متوسط، شتاب گرانش، مرکزگرا و رابطه نیرو و شتاب، آشنا شدیم. در ادامه، برای درک بهتر این مطلب، چند مسئله حل خواهیم کرد.
مسئله ۱
با توجه به نمودار سرعت-زمان نشان داده شده در تصویر زیر، به سوالات پرسیده شده پاسخ دهید. سرعت اولیه در نمودار برابر ۱۰ متر بر ثانیه و به سمت جلو است. جسم، ۸ ثانیه پس از شروع حرکت، متوقف میشود. در ادامه، جسم به مدت ۲ ثانیه به عقب برمیگردد و سرعت آن به ۲/۵ متر بر ثانیه میرسد.
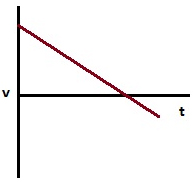
پرسش ۱: جابجایی جسم در ۸ ثانیه اول حرکت را بهدست آورید.
پاسخ: جابجایی برابر مساحت زیر نمودار است. در این حالت، مساحت زیر نمودار برابر مساحت مثلثی به ارتفاع ۱۰ و قاعده ۸ است، زیرا سرعت اولیه جسم برابر ۱۰ متر بر ثانیه است و جسم پس از ۸ ثانیه، متوقف میشود (به سرعت صفر میرسد).
پرسش ۲: اگر مکان اولیه جسم برابر ۱۵- متر باشد، مکان نهایی آن را بهدست آورید.
پاسخ: جابجایی کل جسم برابر مساحت دو مثلث ایجاد شده در زیر نمودار است (مثلث بالای محور افقی و مثلث پایین محور افقی). همانطور که در پرسش اول دیدیم، جابجایی جسم در ۸ ثانیه اول حرکت برابر ۴۰ متر است. به طور مشابه، مساحت مثلت کوچکتر و پایین محور افقی برابر ۲/۵- متر است. در نتیجه، جابجایی کل برابر ۳۷/۵+ متر خواهد بود .
پرسش ۳: شتاب حرکت جسم را بهدست آورید.
پاسخ: شتاب برابر شیب نمودار سرعت-زمان است. از آنجا که شیب نمودار سرعت-زمان ثابت است، شتاب لحظهای و شتاب متوسط با یکدیگر برابر هستند.
مسئله ۲
اتومبیلی به جرم ۱۰۰۰ کیلوگرم، با سرعت مشخصی در حال حرکت است. ناگهان راننده ترمز میکند. نیروی ترمز برابر ۱۰۰۰ نیوتن در مدت زمان ۵ ثانیه بر اتومبیل وارد میشود و سرعت آن را به نصف سرعت اولیه کاهش میدهد. اتومبیل چند ثانیه پس از کاهش سرعت، به طور کامل متوقف خواهد شد. فرض کنید نیروی ترمز تا توقف کامل اتومبیل بر آن وارد میشود.
پاسخ: دادههای مسئله عبارت هستند از:
جرم اتومبیل = 1000 کیلوگرم
نیروی ترمز = 1000 نیوتن
زمان داده شده برای کاهش سرعت به نصف سرعت اولیه = ۵ ثانیه
سرعت اولیه =
سرعت نهایی =
مدت زمان لازم برای توقف کامل اتومبیل را بهدست میآوریم.
بر طبق قانون دوم نیوتن، مقدار نیرو برابر است با:
شتاب متوسط برابر است با:
هنگامی که راننده ترمز میکند، حرکت آن آهسته میشود. بنابراین، مقدار شتاب در خلاف جهت حرکت و منفی خواهد بود.
در پایان، زمان لازم برای توقف را از هنگامی که سرعت اتومبیل نصف سرعت اولیه میشود، بهدست میآوریم:
مسئله ۳
جسمی به جرم ۱۰۰۰ کیلوگرم با سرعت اولیه مشخصی حرکت میکند. نیرویی برابر ۵۰۰ نیوتن بر آن وارد میشود و جسم پس از طی مسافت ۶۴ متر میایستد. سرعت اولیه و زمان لازم برای توقف کامل جسم را بهدست آورید.
پاسخ: دادههای مسئله عبارت هستند از:
جرم جسم = 1000 کیلوگرم
نیروی وارد شده بر جسم = ۵۰۰ نیوتن
سرعت نهایی جسم = صفر متر بر ثانیه
مسافت طی شده تا توقف کامل = ۶۴ متر
بر طبق قانون دوم نیوتن داریم:
از آنجا که نیروی ۵۰۰ نیوتنی جسم را متوقف میکند، شتاب حرکت منفی خواهد بود.
مدت زمان لازم برای توقف برابر است با:
جمعبندی
در این مطلب، در مورد مفهوم شتاب و تفاوت آن با سرعت صحبت کردیم. سپس، فرمول شتاب لحظهای و متوسط را با ذکر مثال توضیح دادیم. در ادامه، در مورد فرمول شتاب مرکزگرا، فرمول شتاب جاذبه گرانش و رابطه بین نیرو و شتاب با حل مثالهای مختلف، صحبت کردیم.













دمت گرم موفقی
ضمن تشکر بابت ارائه این مطلب در خط
“در نتیجه، برای محاسبه سرعت در زمان t=4s …” فکر می کنم در اینجا می بایست “شتاب” به جای “سرعت” استفاده می شد.
با سلام،
متن بازبینی و اصلاح شد،
با تشکر از همراهی شما با مجله فرادرس
سلام. ضمن تشکر بابت ارائه این مقاله قسمت “فرمول شتاب و سرعت چیست ؟” تتو این مقاله به درستی دیده نمی شود. متن و تصویر به هم میریزد. تشکر
با سلام؛
از ارائه بازخورد شما سپاسگزاریم. متن بازبینی و اصلاح شد.
با تشکر از همراهی شما با مجله فرادرس