تراکم پذیری چیست؟ — از صفر تا صد

در علم ترمودینامیک و مکانیک سیالات، تراکم پذیری که گاهی آنرا به صورت ضریب تراکم پذیری یا تراکم پذیری همدما نیز میشناسند، به عنوان معیاری برای سنجش تغییرات نسبی حجم یک مایع یا جامد در پاسخ به تغییر فشار (یا تنش میانگین) است. در تعریفی سادهتر، تراکم پذیری را میتوان به صورت رابطه زیر بیان کرد که در این رابطه، V حجم و P فشار است:
انتخاب علامت منفی در رابطه بالا سبب میشود تا مقدار عددی تراکم پذیری در شرایط معمول، عددی مثبت باشد که در چنین شرایطی، افزایش فشار، سبب کاهش حجم خواهد شد.
تعریف تراکم پذیری
تعریفی که در بالا ارائه شد، تعریف کاملی نیست چراکه برای هر شئ یا سیستم، مقدار تراکم پذیری به نوع فرآیند «همدما» (Isotermal) یا «همآنتروپی» (Isentropic) وابسته است. به این ترتیب، تراکم پذیری همدما به صورت زیر تعریف میشود:
تراکم پذیری را با نماد و با رابطه زیر نیز نشان میدهند:
زیروند T نشان میدهد که در دمای ثابت باید از مشتق جزئی بهره بگیریم. به طور مشابه، تراکم پذیری همدما نیز به صورت زیر خواهد بود:
ارتباط تراکم پذیری با سرعت صوت
تعریف کلاسیک سرعت صوت به شکل زیر است که در آن، به عنوان چگالی در نظر گرفته میشود:
به کمک مشتقات جزئی، تراکم پذیری همآنتروپی (آیزنتروپیک) را میتوان از طریق رابطه زیر بیان کرد:
ضریب حجمی
معکوس تراکم پذیری موسوم ضریب حجمی یا «مدول حجمی» (Bulk Modulus) است که معمولا با یا نشان داده میشود. معادله تراکم پذیری به طور مستقیم تراکم پذیری همدما و به طور غیرمستقیم فشار را با ساختار مایع مرتبط میکند.
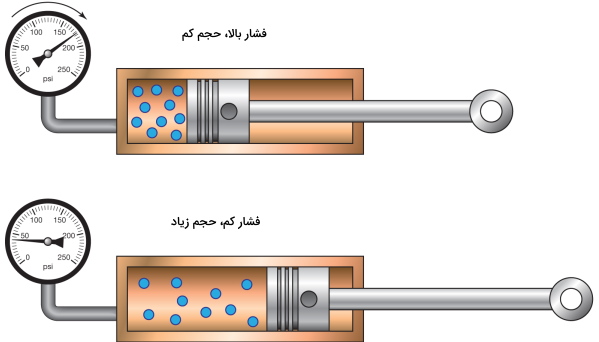
بیان ترمودینامیکی تراکم پذیری
از عبارت تراکم پذیری به طور معمول در ترمودینامیک برای توصیف انحراف در خواص ترمودینامیکی یک گاز واقعی از حالت ایدهآل استفاده میشود. در این رابطه به طور معمول از ضریب تراکم پذیری با تعریف زیر بهره میگیرند:
- : فشار
- : دما
- : حجم مولی
اگر ضریب تراکم پذیری برابر با ۱ باشد، آنگاه به تعریف گاز ایدهآل خواهیم رسید. اما این ضریب برای گاز واقعی، میتواند کمتر یا بیشتر از ۱ باشد.
انحراف از رفتار گاز ایدهآل در نزدیکی نقطه بحرانی و همچنین در شرایط فشار زیاد یا دمای پایین، به شدت افزایش مییابد. در چنین شرایطی از نمودارهای تراکم پذیری یا معادلات حالت برای حصول نتایج دقیق استفاده میشود. چنین حالاتی در سرعتهای مافوق صوت هوا بوقوع میپیوندند و حجم مولی تفکیک افزایش پیدا میکند چراکه یک مول اکسیژن به صورت به دو مول اکسیژن تکاتمی تبدیل و به طور مشابه ، نیز به به تبدیل میشود. در فشارهای متوسط و دمای بالاتر از 10000 کلوین، گاز به الکترونهای آزاد و یونها تفکیک خواهد شد. تراکم پذیری همدما به کمک رابطه زیر به تراکم پذیری همآنتروپی مرتبط میشود:
به کمک روابط ماکسول در ترمودینامیک، این رابطه سادهتر خواهد شد که در این معادله، موسوم به نسبت ظرفیت حرارتی است:
انبساط پذیری هم فشار
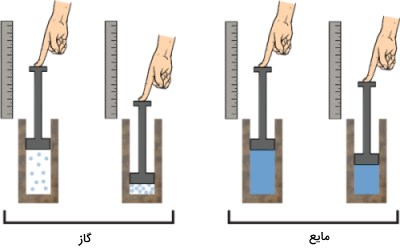
از جمله خواص مهم مواد، نحوه تغییرات حجم در اثر تغییرات دما است. با توجه به قانون شارل، گازها نسبت به مایعات و جامدات، این تغییرات را بهتر نشان میدهند. در تعریف انبساط پذیری همفشار یا به عبارت دیگر ضریب انبساط، از رابطه زیر بهره میگیریم:
توجه داشته باشید که برای اینکه این عبارت را به خاصیت شدتی تبدیل کنیم، عبارت مورد نیاز بود. زمانی که انبساط داشته باشیم، با افزایش دما، حجم نیز افزایش مییابد و در نتیجه، مقدار عددی مشتق جزئی، مثبت خواهد بود.
مثال برای روابط تراکم پذیری
رابطهای را برای بدست آورید.
با توجه به روابط مطرح شده در بالا، رابطه زیر را برای حل سوال مینویسیم:
با سادهسازی عبارت بالا، به رابطه زیر میرسیم:
در نهایت، با استفاده از قوانین مشتق جزئی، رابطه زیر را خواهیم داشت:
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس شیمی
- مجموعه آموزشهای مهندسی شیمی
- آموزش شیمی عمومی
- مخلوط گازها — به زبان ساده
- قانون بویل — به زبان ساده
- جدول تناوبی — از صفر تا صد
^^












با سلام و احترام
ضمن تشكر از مطالب علمي كه ارائه داديد يك سوال داشتم.
براي سيالات ضريب تراكم پذيري و ضريب تراكم ناپذيري وجود دارد اگر درست متوجه شده باشم. سوالم اينجاست كه وقتي ضريب تراكم ناپذيري عكس ضريب تراكم پذيري مي باشد چه لزومي دارد كه هر دو ضريب بيان شود؟
سپاس
سپاس از پاسخ شما
درست مي فرماييد اشاره اي نشده، ولي برای سیالات ضریب تراکم پذیری و ضریب تراکم ناپذیری تعريف مي شود. همانطور كه در پيام قبل اشاره كردم دليل اينكه هر دو ضريب مورد استفاده قرار مي گيرد چيست وقتي اين دو ضريب عكس هم هستند. مثلا در علم مكانيك جرم مخصوص و حجم مخصوص داريم كه عكس هم هستند از نظر فرمولي ولي در اولي به دنبال مشخص كردن جرم 1 مترمكعب از ماده هستيم ولي در دومي در پي مشخص كردن حجم 1 كيلوگرم از ماده. ولي براي ضريب تراكم پذيري و تراكم ناپذيري به نتيجه نرسيدم كه چرا بايد هر دو وجود داشته باشد.
سپاس
با سلام؛
در داخل متن، عبارتی با نام ضریب تراکمناپذیری ذکر نشده است.
با تشکر از همراهی شما با مجله فرادرس
علت تفاوت ضریب تراکم پذیری آب و جیوه و هوا چیه؟ چرا ضریب آب بیشتر از جیوه اس؟؟
با سلام؛
از شما بابت مطالعه این مطلب سپاسگزاریم.
تفاوت اصلی در تراکمپذیری مواد به خوبی در تعریف آن دیده شده است اما دلیل تغییر متفاوت حجم در اثر فشار را میتوان در مایعات، با نیروهای بینمولکولی و در گازها با رفتار متفاوت بین گاز واقعی (انحراف از رفتار ایدهآل تعریف آن با فاکتور Z) و گاز ایدهآل بیان کرد.
با تشکر
سلام یه سوال داشتم ممنون میشم جواب بدید
ضریب تراکم پذیری جیوه اب و هوا چقدره
کلی گشتم ولی چیزی پیدا نکردم
با سلام؛
از شما بابت مطالعه مطلب سپاسگزاریم. در کتب مرجع مکانیک سیالات و مهندسی شیمی و نفت، این اعداد یافت میشوند که البته همانطور که در متن ذکر شده، ممکن است بسته به نوع فرآیند، این عدد متفاوت باشد به همین دلیل، با رجوع به این کتب مرجع، مقادیر با شرایط مختلف ذکر شدهاند. با این وجود، مقدار تراکم پذیری برای جیوه و آب به ترتیب برابر با 3.7×10−11 Pa−1 و 45.8×10−11 Pa−1 است. برای هوا نیز بر اساس دما، مقادیر مختلفی ذکر میشود که برای دسترسی به این مقادیر کافی است تا عبارت «air compressibility factor» را جستجو کنید.
با تشکر