محاسبه فشار سیال — به زبان ساده

در آموزشهای پیشین مجله فرادرس، با نحوه محاسبه جریان سیال آشنا شدیم. در این آموزش، روش محاسبه فشار سیال را بیان میکنیم.
فشار سیال و قانون پاسکال
همانطور که میدانیم، فشار برابر با نسبت نیرو به واحد سطح است:
$$ \large P = \frac { F } { A } . $$
اگر جسمی در یک مایع به عمق $$ h $$ غوطهور شود، فشار سیال با فرمول عمق ثابت بیان خواهد شد:
$$\large P = \rho gh, $$
که در آن، $$ \rho $$ چگالی سیال و $$ g $$ شتاب گرانش است.
فشار سیال یک کمیت نردهای است. این کمیت جهت ندارد و بنابراین، یک سیال در همه جهات فشار برابری وارد میکند. این بیان به عنوان «قانون پاسکال» (Pascal’s law) شناخته میشود و توسط دانشمند فرانسوی، «بلز پاسکال» (Blaise Pascal) کشف شد.
حالتی را در نظر بگیرید که یک صفحه عمودی را که با خطوط زیر محدود شده است:
$$ \large { x = a , \; \; } \kern0pt { x = b , \; \; } \kern0pt { y = f \left ( x \right ) , \; \; } \kern0pt { y = g \left ( x \right ) } $$
در یک مایع غوطهور کردهایم.
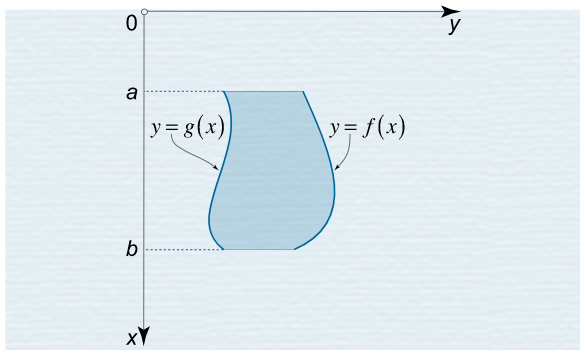
از آنجا که نقاط مختلف ورقه عمقهای متفاوتی دارند، نیروی هیدرواستاتیک $$ F $$ اعمالی روی ورقه با انتگرال زیر به دست میآید:
$$ \large F = \rho g \int \limits _ a ^ b { \left [ { f \left ( x \right ) – g \left ( x \right ) } \right ] x d x } . $$
این فرمول اغلب به عنوان فرمول عمق متغیر برای نیروی سیال شناخته میشود.
مثالهای محاسبه فشار سیال
در این بخش چند مثال را بررسی میکنیم.
مثال ۱
یک مخزن استوانهای با ارتفاع ۳ متر و شعاع قاعده ۱ متر از گازوئیل پر شده است. نیروی هیدرواستاتیک اعمالی به جداره مخزن را در صورتی بیابید که چگالی گازوئیل $$800\,\large{\frac{{\text{kg}}}{{{\text{m}^3}}}}\normalsize $$ باشد.
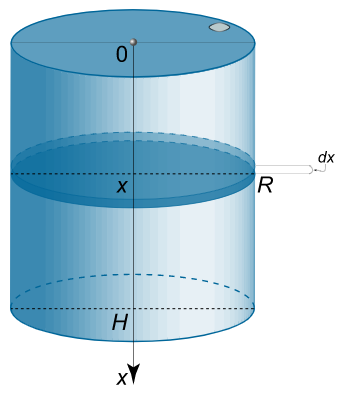
حل: محور $$ x $$ در جهت عمودی و به سمت پایین و مبدأ مختصات را نقطه مرکز قاعد بالایی استوانه در نظر میگیریم.
یک لایه نازک در عمق $$ x $$ را در نظر بگیرید. اگر ضخامت آن $$ dx $$ باشد، سطح جانبی این لایه به صورت زیر خواهد بود:
$$ \large d A = 2 \pi R d x . $$
فشار سیال در عمق $$ x $$ برابر با $$P = \rho gx $$ است. بنابراین، نیروی اعمالی سیال به سطح جانبی به صورت زیر خواهد بود:
$$ \large d F = P d A = 2 \pi \rho g R x d x . $$
برای یافتن کل نیروی هیدرواستاتیک $$ F $$، از $$ x = 0 $$ تا $$ x = H $$ انتگرال میگیریم:
$$ \large \require {cancel} { F = \int \limits _ 0 ^ H { d F } } = { 2 \pi \rho g R \int \limits _ 0 ^ H { x d x } } = { \left . { \frac { { \cancel { 2 } \pi \rho g R { x ^ 2 } } } { \cancel { 2 } } } \right | _ 0 ^ H } = { \left . { \pi \rho g R { x ^ 2 } } \right | _ 0 ^ H } = { \pi \rho g R { H ^ 2 } . } $$
با جایگذاری مقادیر داده شده در فرمول، داریم:
$$ \large { F = \pi \times 8 0 0 \times 9 . 8 \times 1 \times { 3 ^ 2 } } \approx { 2 2 1 6 7 1 \, \text {N} }\approx { 2 2 2 \, \text {kN} . } $$
مثال ۲
یک استخر شنای مستطیلی دارای عمق $$ H $$ عرض $$ a $$ و طول $$ b $$ است. موارد زیر را محاسبه کنید:
- (الف) نیروی سیال $$F_{ab} $$ که به کف استخر وارد میشود.
- (ب) نیروی سیال $$F_{aH} $$ که روی هر جداره $$\left({a \times H}\right)\text{m} $$ وارد میشود.
- (ج) نیروی سیال $$F_{bH} $$ که روی هر جداره $$\left({b \times H}\right)\text{m} $$ وارد میشود.

حل (الف): فشار در کف استخر برابر با $$P = \rho gH $$ است، بنابراین، نیروی هیدرواستاتیک وارد شده به کف برابر خواهد بود با:
$$ \large { F _ { a b } } = P A = \rho g H A = \rho g a b H . $$
حل (ب): برای تعیین نیروی روی $$ \left({a \times H}\right)\text{m} $$ جداره استخر، یک نوار نازک به ضخامت $$ d x $$ در عمق $$ x $$ را در نظر میگیریم.

مساحت نوار $$ d A = a d x $$ است. از آنجا که فشار آب در عمق $$ x $$ برابر با $$P = \rho gx $$ است، نیروی اعمالی بر نوار اولیه به صورت زیر است:
$$ \large d F = P d A = \rho g a x d x . $$
کل نیروی روی جداره $$ \left({a \times H}\right)\text{m} $$ با انتگرالگیری زیر محاسبه میشود:
$$ \large { F _ { a H } = \int \limits _ 0 ^ H { d F } } = { \int \limits _ 0 ^ H { d F } } = { \rho g a \int \limits _ 0 ^ H { x d x } } = { \left . { \frac { { \rho g a { x ^ 2 } } } { 2 } } \right | _ 0 ^ H } = { \frac { { \rho g a { H ^ 2 } } } { 2 } . } $$
حل (ج): مشابه قسمت قبل، نیروی وارد شده به جداره $$\left({b \times H}\right)\text{m} $$ استخر، برابر است با:
$$ \large { F _ { b H } } = \frac { { \rho g b { H ^ 2 } } } { 2 } .$$
مثال ۳
یک صفحه مثلثی به قاعده $$ a $$ و ارتفاع $$ H $$ به صورت عمودی در آب غوطهور شده است به گونهای که قاعده آن بر سطح آب منطبق است. نیروی هیدرواستاتیک وارد شده به هر یک از جدارههای این صفحه را بیابید.
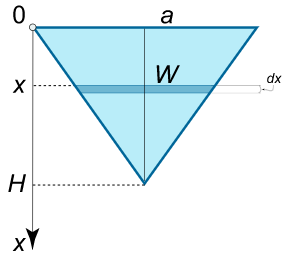
حل: با استفاده از تشابه مثلثها، داریم:
$$ \large { \frac { W } { a } = \frac { { H – x } } { H } , } \; \; \Rightarrow { W = a – \frac { a } { H } x . } $$
مساحت نوار افقی اولیه در عمق $$ x $$ برابر است با:
$$ \large { d A = W d x } = { \left ( { a – \frac { a } { H } x } \right ) d x . } $$
فشار آب در عمق $$ x $$ برابر است با $$P = \rho gx $$. بنابراین، نیروی وارد شده بر نوار به صورت زیر نوشته میشود:
$$ \large { d F = P d A } = { \rho g x \left ( { a – \frac { a } { H } x } \right ) d x } = { \rho g a x \left ( { 1 – \frac { x } { H } } \right ) d x . } $$
کل نیرو به صورت زیر محاسبه میشود:
$$ \large \begin {align*} F & = \int\limits _ 0 ^ H { d F } = { \rho g a \int \limits _ 0 ^ H { x \left ( { 1 – \frac { x } { H } } \right ) d x } } \\ &= { \rho g a \int \limits _ 0 ^ H { \left ( { x – \frac { { { x ^ 2 } } } { H } } \right ) d x } } = { \rho g a \left . { \left [ { \frac { { { x ^ 2 } } } { 2 } – \frac { { { x ^ 3 } } } { { 3 H } } } \right ] } \right | _ 0 ^ H } \\ & = { \rho g a \left ( { \frac { { { H ^ 2 } } } { 2 } – \frac { { { H ^ 3 } } } { { 3 H } } } \right ) } = { \frac { { \rho g a { H ^ 2 } } } { 6 } . } \end {align*} $$
مثال ۴
مکعبی به اضلاع $$ a $$ در آب غوطهور شده است، به گونهای که سطح بالایی آن موازی با سطح آب و $$ H $$ متر پایینتر از آن است. کل نیروی هیدرواستاتیک وارد شده بر مکعب را بیابید.
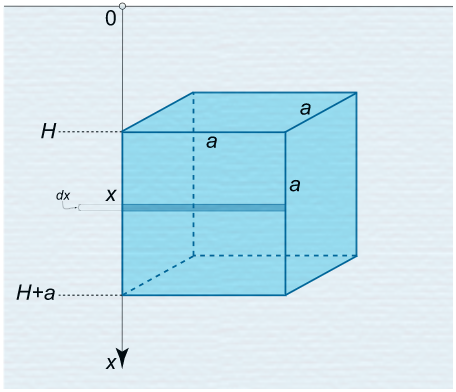
حل: با استفاده از فرمول عمق ثابت، به سادگی نیروی اعمالی بر سطح بالایی به دست میآید:
$$ \large { F _ { t o p } } = { P _ { t o p } } A = \rho g { a ^ 2 } H . $$
به طور مشابه، نیروی روی سطح زیرین به صورت زیر است:
$$ \large { { F _ { b o t t o m } } = { P _ { b o t t o m } } A } = { \rho g { a ^ 2 } \left ( { H + a } \right ) } = { \rho g { a ^ 2 } H + \rho g { a ^ 3 } . } $$
برای تعیین نیروی وارد بر جدارهها، یک نوار نازک افقی به ضخامت $$ d x $$ و عمق $$ x $$ در نظر میگیریم. مساحت این نوار $$ d A = a d x $$ است. فشار آب در این عمق $$ P = \rho g x $$ است. در نتیجه، نیروی هیدرواستاتیکی $$ d F $$ وارد شده بر نوار به صورت زیر خواهد بود:
$$ \large d F = P d A = \rho g a x d x . $$
بنابراین، کل نیروی وارده بر یک وجه مکعب برابر خواهد بود با:
$$ \large \begin {align*} { F _ { s i d e } } & = \int \limits _ H ^ { H + a } { d F } = { \rho g a \int \limits _ H ^ { H + a } { x d x } } = { \left . { \frac { { \rho g a { x ^ 2 } } } { 2} } \right | _ H ^ { H + a } } = { \frac { { \rho g a } } { 2 } \left [ { { { \left ( { H + a } \right ) } ^ 2 } – { H ^2 } } \right ] } \\ & = { \frac { { \rho g a } } { 2 } \left ( { \cancel { { H ^ 2 } } + 2 a H + { a ^ 2 } - \cancel { { H ^ 2 } } } \right ) } = { \rho g { a ^ 2 } H + \frac { { \rho g { a ^ 3 } } } { 2 } . } \end {align*} $$
در نهایت، کل نیروی هیدرواستاتیک وارده بر مکعب برابر است با:
$$ \large \begin {align*} F & = { F _ { t o p } } + { F _ { b o t to m } } + 4 { F _ { s i d e } } \\ &= { \rho g { a ^ 2 } H + \rho g { a ^ 2 } H } + { \rho g { a ^ 3 } } + { 4 \left ( { \rho g { a ^ 2 } H + \frac { { \rho g { a ^ 3 } } } { 2 } } \right ) } \\ &= { 6 \rho g { a ^ 2 } H + 3 \rho g { a ^ 3 } } = { 3 \rho g { a ^ 2 } \left ( { 2 H + a } \right ) . } \end {align*} $$
مثال ۵
یک صفحه مستطیلی با اضلاع $$ a $$ و $$ b $$ ($$ a > b $$) با زاویه $$ \alpha $$ در سطح آب غوطهور است. ضلع بلندتر موازی با سطح آب است و در عمق $$ H $$ از آن قرار دارد. نیروی وارد شده به هریک از اضلاع را بیابید.
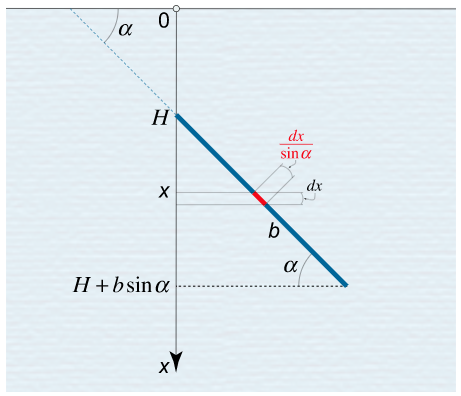
حل: طبق قانون پاسکال، فشار سیال در عمق $$ x $$ در هر جهت برابر با $$P = \rho gx $$ است. بنابراین، اگر یک نوار کوچک را روی صفحه در عمق $$ x $$ و متناظر با نمو $$ d x $$ در نظر بگیریم، نیروی اعمالی بر نوار به صورت زیر خواهد بود:
$$ \large { d F = P d A } = { \rho g x \times \frac { { a d x } } { { \sin \alpha } } } = { \frac { { \rho g a x d x } } { { \sin \alpha } } . } $$
کل نیروی هیدرواستاتیکی با انتگرال زیر به دست میآید:
$$ \large \begin {align*} F & = \int \limits _ H ^ { H + b \sin \alpha } { d F } = { \frac { { \rho g a } } { { \sin \alpha } } \int \limits _ H ^ { H + b \sin \alpha } { x d x } } = { \frac { { \rho g a } } { { \sin \alpha } } \left . { \frac { {{ x ^ 2 } } } { 2 } } \right | _ H ^ { H + b \sin \alpha } } \\ & = { \frac { { \rho g a } } { { 2 \sin \alpha } } \left [ { { { \left ( { H + b \sin \alpha } \right ) } ^ 2 } – { H ^ 2 } } \right ] } = { \frac { { \rho g a } } { { 2 \sin \alpha } } \left ( { 2 b H \sin \alpha + { b ^ 2 } { { \sin } ^ 2 } \alpha } \right ) } \\ & = { \rho g a b \left ( { H + \frac { b } { 2 } \sin \alpha } \right ) . } \end {align*} $$
مثال ۶
یک سد به شکل ذوزنقه متساویالساقین با قاعده بالایی $$a = 64\,\text{m} $$، قاعده پایینی $$b = 42\,\text{m} $$ و ارتفاع آن $$H = 3\,\text{m} $$ است. نیروی ناشی از فشار هیدرواستاتیک روی سد را بیابید.
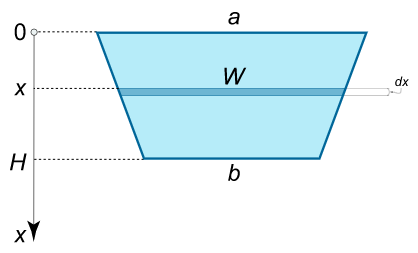
حل: اگر محور $$ x $$ عمودی را به سمت پایین انتخاب کنیم، فشار سیال در عمق $$ x $$ به صورت زیر نوشته میشود:
$$ \large P = \rho gx. $$
یک نوار افقی باریک به عرض $$ dx $$ در عمق $$ x $$ را میتوان با یک مستطیل به مساحت زیر تقریب زد:
$$ \large dA = Wdx, $$
که عرض $$ W $$ ذوزنقه در عمق $$ x $$ از تشابه مثلثها تعیین میشود:
$$ \large W = a – \left ( { a – b } \right ) \frac { x } { H } . $$
در نتیجه، نیروی هیدرواستاتیک اعمالی بر نوار با فرمول زیر بیان میشود:
$$ \large { d F = P d A } = { \rho g x \left [ { a – \left ( { a – b } \right ) \frac { x } { H } } \right ] d x . } $$
کل نیروی ناشی از فشار هیدرواستاتیک وارد بر سد به صورت زیر است:
$$ \large \begin {align*} F & = \int \limits _ 0 ^ H { d F } = { \rho g \int \limits _ 0 ^ H { x \left [ { a – \left ( { a – b } \right ) \frac { x } { H } } \right ] d x } } = { \rho g \int \limits _ 0 ^ H { \left ( { a x – \frac { { a – b } } { H } { x ^ 2 } } \right ) d x } } \\ & = { \rho g \left . { \left [ { \frac { { a { x ^ 2 } } } { 2 } – \frac { { \left ( { a – b } \right ) { x ^ 3 } } } { { 3 H } } } \right ] } \right | _ 0 ^ H } = { \rho g \left [ { \frac { { a { H ^ 2 } } } { 2 } – \frac { { \left ( { a – b } \right ) { H ^ 2 } } } { 3 } } \right ] } = { \rho g { H ^ 2 } \left ( { \frac { a } { 6 } + \frac { b } { 3 } } \right ) . } \end {align*} $$
اکنون میتوانیم به سادگی مقدار نیرو را محاسبه کنیم:
$$ \large { F = 1 0 0 0 \times 9 . 8 \times { 3 ^ 2 } \times \left ( { \frac { { 6 . 4 } } { 6 } + \frac { { 4 . 2 } } { 3 } } \right ) } = { 2 1 7 5 6 0 \, \text {N} } \approx { 2 1 8 \, \text {kN} . } $$
مثال ۷
یک مخروط دایرهای قائم با شعاع قاعده $$ R $$ و ارتفاع $$ H $$ به گونهای در آب غوطهور است که رأس آن به سمت پایین و قاعدهاش موازی با سطح آب است. نیروی ناشی از فشار هیدرواستاتیک اعمال شده بر سطح جداره مخروط را محاسبه کنید.
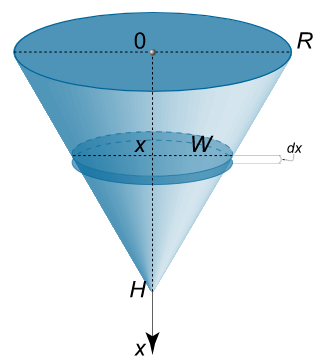
حل: طبق تشابه مثلثها، رابطه زیر را داریم:
$$ \large { \frac { W } { { H – x } } = \frac { R } { H } , } \; \; \Rightarrow { W = \frac { { R \left ( { H – x } \right ) } } { H } = R \left ( { 1 – \frac { x } {H } } \right ) . } $$
مساحت سطح یک نوار کوچک از مخروط در نقطه $$ x $$ به صورت زیر است:
$$ \large { d A = 2 \pi W d x } = { 2 \pi R \left ( { 1 – \frac { x }{ H } } \right ) d x . } $$
فشار در تمام جهات در عمق $$ x $$ برابر با $$ P = \rho gx $$ است. بنابراین، نیروی وارد بر نوار به صورت زیر خواهد بود:
$$ \large { d F = P d A } = { 2 \pi \rho g R x \left ( { 1 – \frac { x } { H } } \right ) d x . } $$
نیروی کل با انتگرالگیری از $$ x = 0 $$ تا $$ x = H $$ به دست میآید:
$$ \large \begin {align*} F & = \int \limits _ 0 ^ H { d F } = { 2 \pi \rho g R \int \limits _ 0 ^ H { x \left ( { 1 – \frac { x } { H } } \right ) d x } } = { 2 \pi \rho g R \int \limits _ 0 ^ H { \left ( { x – \frac { { { x ^ 2 } } } { H } } \right ) d x } } \\ & = { 2 \pi \rho g R \left . { \left ( { \frac { { { x ^ 2 } } } { 2 } – \frac { { { x ^ 3 } } } { { 3 H } } } \right ) } \right | _ 0 ^ H } = { 2 \pi \rho g R \left ( { \frac { { { H ^ 2 } } } { 2 } – \frac { { { H ^ 3 } } } { { 3 H } } } \right ) } = { \frac { { \pi \rho g R { H ^ 2 } } } { 3 } . } \end {align*} $$
مثال ۸
صفحهای به شکل متوازیالاضلاع با اضلاع $$ a $$ و $$ b $$ و زاویه $$ \alpha $$ به صورت عمودی در آب غوطهور شده است به گونهای که ضلع $$ b $$ در سطح آب قرار دارد. نیروی هیدرو استاتیک وارد بر هر ضلع را به دست آورید.
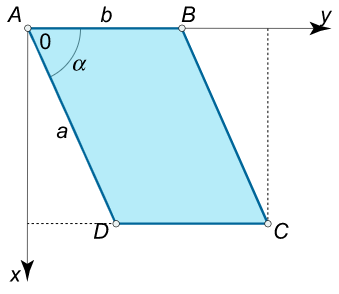
حل: رئوس $$ ABCD $$ متوازیالاضلاع به صورت زیر هستند:
$$ \large { A \left ( { 0 , 0 } \right ) , \; \; } \kern0pt { B \left ( { 0 , b } \right ) , \; \; } \kern0pt { C \left ( { a \sin \alpha , b + a \cos \alpha } \right ) , \; \; } \kern0pt { D \left ( { a \sin \alpha , a \cos \alpha } \right ) . } $$
معادله ضلع $$ A D $$ را مینویسیم. با استفاده از فرم دونقطهای معادله خط راست، داریم:
$$ \large \frac { { x – { x_ A } } } { { { x _ D } – { x _ A } } } = \frac { { y – { y _ A } } } { { { y _ D } – { y _ A } } } , \; \; \Rightarrow { \frac { { x – 0 } } { { a \sin \alpha – 0 } } = \frac { { y – 0 } } { { a \cos \alpha – 0 } } , } \; \; \\ \large \Rightarrow { \frac { x } { { a \sin \alpha } } = \frac { y } { { a \cos \alpha } } , } \; \; \Rightarrow { { y _ 1 } = x \cot \alpha . } $$
ضلع $$ B C $$ به اندازه $$ b $$ واحد در طول محور $$ y $$ به بالا جابهجا شده است، بنابراین، معادله آن به صورت زیر است:
$$ \large { y _ 2 } = b + x \cot \alpha . $$
اکنون از فرمول عمق متغیر استفاده میکنیم:
$$ \large F = \rho g \int \limits _ a ^ b { \left [ { f \left ( x \right ) – g \left ( x \right ) } \right ] x d x } . $$
در نتیجه، کل نیروی وارد بر صفحه برابر است با:
$$ \require {cancel} \large \begin {align*} F & = \rho g \int \limits _ 0 ^ { a \sin \alpha } { \left ( { { y _ 2 } – { y _ 1 } } \right ) x d x } = { \rho g \int \limits _ 0 ^ { a \sin \alpha } { \left ( { b + \cancel { x \cot \alpha } – \cancel { x \cot \alpha } } \right ) x d x } } \\ & = { \rho g b \int \limits _ 0 ^ { a \sin \alpha } { x d x } } = { \left . { \frac { { \rho g b { x ^ 2 } } } { 2 } } \right | _ 0 ^ { a \sin \alpha } } = { \frac { { \rho g b { a ^ 2 } { { \sin } ^ 2 } \alpha } } { 2 } . } \end {align*} $$
مثال ۹
نصف دیسکی به شعاع $$ R $$ به صورت عمودی درون مایعی با چگالی $$ \rho $$ قرار دارد. نیروی هیدرواستاتیک وارد بر یک جنب دیسک را بیابید.
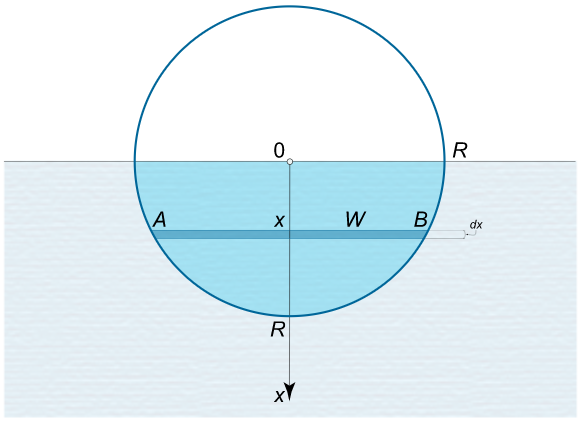
حل: یک نوار افقی به ضخامت $$ d x $$ را در عمق $$ x $$ در نظر بگیرید. عرض نوار برابر است با:
$$ \large W = A B = 2 \sqrt { { R ^ 2 } – { x ^ 2 } } $$
بنابراین، مساحت آن به صورت زیر خواهد بود:
$$ \large { d A = W d x } = { 2 \sqrt { { R ^ 2 } – { x ^ 2 } } d x . } $$
نیروی روی نوار تقریباً برابر است با:
$$ \large { d F = P d A } = { \rho g x d A } = { 2\rho g x \sqrt { { R ^ 2 } – { x ^ 2 } } d x . } $$
کل نیروی هیدرواستاتیک با انتگرال زیر بیان میشود:
$$ \large { F = \int \limits _ 0 ^ R { d F } } = { 2 \rho g \int \limits _ 0 ^ R { x \sqrt { { R ^ 2 } – { x ^ 2 } } d x } . } $$
این انتگرال را با استفاده از روش تغییر متغیر حل میکنیم:
$$ \large \begin {align*} I & = \int { x \sqrt { { R ^ 2 } – { x ^ 2 } } d x } = { \left [ { \begin {array} { * { 2 0 } { l } }
{ z = { R ^ 2 } – { x ^ 2 } } \\
{ d z = – 2 x d x }
\end {array} } \right ] } = { \int { \sqrt z \left ( { – \frac { { d z } } { 2 } } \right ) } } \\ & = { – \frac { 1 } { 2 } \int { \sqrt z d z } } = { – \frac { { { z ^ { \frac { 3 } { 2 } } } } } { 3 } } = { – \frac { { \sqrt { { z ^ 3 } } } } { 3 } } = { – \frac { { \sqrt { { { \left ( { { R ^ 2 } – { x ^ 2 } } \right ) } ^ 3 } } } } { 3 } . } \end {align*} $$
بنابراین، نیروی $$ F $$ به صورت زیر خواهد بود:
$$ \large { F = – \frac { { 2 \rho g } } { 3 } \left . { \sqrt { { { \left ( { { R ^ 2 } – { x ^ 2 } } \right ) } ^ 3 } } } \right | _ 0 ^ R } = { – \frac { { 2 \rho g } } { 3 } \left ( { 0 – { R ^ 3 } } \right ) } = { \frac { { 2 \rho g { R ^ 3 } } } { 3 } . } $$
مثال ۱۰
صفحهای به شکل یک قطعه سهمی به صورت عمودی در آب قرار دارد. قاعده آن برابر با $$ 2 a $$ و ارتفاع آن $$ H $$ است. نیروی ناشی از فشار هیدرواستاتیکی روی هر وجه این صفحه را بیابید.
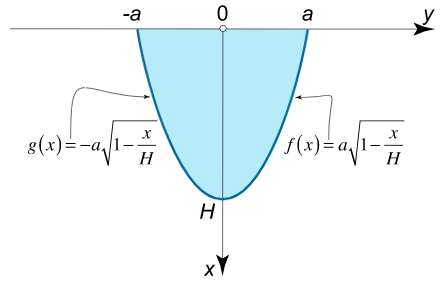
حل: ابتدا معادله سهمی را با قاعده $$ 2 a $$ و ارتفاع $$ H $$ به دست میآوریم. معادله اولیه $$x = H – k{y^2} $$ است. از آنجا که در نقطه $$ x = 0 $$ مقدار $$ y =a $$ را داریم، ضریب $$ k $$ برابر است با:
$$ \large { 0 = H – k { a ^ 2 } , } \; \; \Rightarrow { k = \frac { H } { { { a ^ 2 } } } . } $$
در نتیجه، داریم:
$$ \large { x = H – \frac { H } { { { a ^ 2 } } } { y ^ 2 } } = { H \left ( { 1 – \frac { { { y ^ 2 } } } { { { a ^ 2 } } } } \right ) . } $$
با حل معادله برای $$ y $$، خواهیم داشت:
$$ \large { \frac { x } { H } = 1 – \frac { { { y ^ 2 } } }{ { { a ^ 2 } } } , } \; \; \Rightarrow { { a ^ 2 } – { y ^ 2 } = { a ^ 2 } \frac { x } { H } , } \; \; \Rightarrow { { y ^ 2 } = { a ^ 2 } \left ( { 1 – \frac { x } { H } } \right ) . } $$
بنابراین، این قطعه سهمی با منحنیهای زیر محدود شده است:
$$ \large { y = g \left ( x \right ) = – a \sqrt { 1 – \frac { x } { H } } , \; \;} \kern0pt { y = f \left ( x \right ) = a \sqrt { 1 – \frac { x } { H } } . } $$
برای محاسبه نیروی هیدرواستاتیک، از فرمول عمق متغیر استفاده میکنیم:
$$ \large F = \rho g \int \limits _ a ^ b { \left [ { f \left ( x \right ) – g \left ( x \right ) } \right ] x d x } . $$
برای این مثال، داریم:
$$ \large F = 2 \rho g a \int \limits _ 0 ^ H { \sqrt { 1 – \frac { x } { H } } x d x } . $$
از تغییر متغیر زیر استفاده میکنیم:
$$ \large { 1 – \frac { x } { H } = { z ^ 2 } , } \; \; \Rightarrow { x = H ( 1 – { z ^ 2 } ) , \; \; } \kern0pt { d x = – 2 H z d z . } $$
اگر $$ x = 0 $$ باشد، $$ z = 1 $$ و وقتی $$ x = H $$ باشد، آنگاه $$ z = 0 $$ خواهد بود. در نتیجه، داریم:
$$ \large \begin {align*} F & = – 4 \rho g a { H ^ 2 } \int \limits _ 1 ^ 0 { z \left ( { 1 – { z ^ 2 } } \right ) z d z } = { 4 \rho g a { H ^ 2 } \int \limits _ 0 ^ 1 { \left ( { { z ^ 2 } – { z ^ 4 } } \right ) d z } } \\ & = { 4 \rho g a { H ^ 2 } \left . { \left ( { \frac { { { z ^ 3 } } } { 3 } – \frac { { { z ^ 5 } } } { 5 } } \right ) } \right | _ 0 ^ 1 } = { 4 \rho g a { H ^ 2 } \left ( { \frac { 1 } { 3 } – \frac { 1 } { 5 } } \right ) } = { \frac { { 8 \rho g a { H ^ 2 } } } { { 1 5 } } . } \end {align*} $$
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس فیزیک
- آموزش فیزیک پایه ۱
- مجموعه آموزشهای ریاضیات و فیزیک پایه
- آموزش فیزیک ۱ دانشگاهی با رویکرد حل مساله
- گزارش کار آزمایشگاه — اصول نگارش
- اپلیکیشن Phyphox — آزمایشگاه فیزیکی در جیب شما
- نانو (Nano) — به زبان ساده
^^











عالی