کار در ترمودینامیک — از صفر تا صد
کار در ترمودینامیک و علم شیمیفیزیک، به انرژی منتقل شده از سیستم به محیط میگویند و این انتقال انرژی با مکانیسمی انجام میشود که سیستم به طور خودبهخودی نیروی ماکروسکوپی بر محیط اعمال کند و این نیرو قابل اندازهگیری باشد. این کار انجام شده روی محیط، به کمک اتصالات مناسبی میتواند وزنی را جابجا (بلند) کند. علامت این کار انجام شده توسط سیستم بر روی محیط، منفی خواهد بود. البته در شیمی از علامت مثبت استفاده میکنند. در تعریفی دیگر، کار در ترمودینامیک را به صورت زیر تعریف میکنند:
هر مقداری از انرژی که در طول مرز بین سیستم و محیط جریان یابد و نتیجه اعمال نیرو در یک فاصله مشخص باشد به عنوان کار در ترمودینامیک شناخته میشود. به عنوان مثال میتوان به حرکت یک یون در محلول از یک ناحیه به ناحیه دیگر اشاره کرد. همچنین، باد شدن بالون یا بالا رفتن از پلهها را نیز میتوان از دیگر نمونههای کار در ترمودینامیک دانست. در هرکدام از این مثالها، نیرویی در جهت حرکت وجود دارد.
نیروهای اندازهگیری شده خارجی و همچنین اثرات خارجی میتوانند به صورت متغیرهای الکترومغناطیسی، گرانشی، فشار-حجم و سایر متغیرهای مکانیکی باشند. برای کار در ترمودینامیک یا کار ترمودینامیکی، این مقادیر خارجی، دقیقا با مقادیر تغییرات ماکروسکوپی تابع حالت برابر است. کار در ترمودینامیک، نوع خاصی از مفهوم کار در فیزیک به شمار میآید. در سیستم SI، کار با واحد ژول تعریف میشود و نرخ انجام کار نیز، «توان» (Power) نام دارد.
مقدمه
زمانی که افراد به طور کلی در خصوص کار صحبت میکنند، منظور آنها از کار، تلاش برای انجام یک فعالیت است. ممکن است شخصی بر روی یک پروژه درسی یا برای پیشرفت ورزش در رشتهای خاص کار کند. اما کار در ترمودینامیک تعریف مخصوص به خود را دارد. علاوه بر تعاریفی که در بالا ارائه شد، کار در ترمودینامیک را میتوان به شکل زیر هم تعریف کرد:
به انرژی صرف شده برای حرکت یک شی در خلاف جهت نیرو، کار میگویند. زمانی که سیستم بر روی محیط کار انجام میدهد، انرژی درونی سیستم کاهش پیدا میکند. زمانی که بر روی سیستم کار انجام شود، انرژی درونی آن افزایش مییابد. همچون گرما، تغییرات انرژی به شکل کار، به عنوان بخشی از یک فرآیند انجام میشوند به این معنی که یک سیستم میتواند کار انجام دهد اما خود سیستم شامل کار نیست.

محاسبه کار در ترمودینامیک
برای محاسبه کار انجام شده توسط یک نیروی ثابت، از رابطه کلی زیر استفاده میکنیم:
جابجایی $$\times$$ نیرو = کار
از این رابطه درمییابیم که کار با نیرو و جابجایی، رابطه مستقیم دارد. برخی از مثالهای ساده برای کار در زیر آورده شدهاند:
- شخصی که کتابی را از زمین به داخل قفسه کتابخانه میگذارد، در مقابل گرانش کار انجام داده است.
- باتری که جریان الکتریکی در مدار را سبب میشود، در مقابل مقاومت، کار انجام میدهد.
- زمانی که جعبهای را روی زمین هل میدهیم، در مقابل اصطکاک کار انجام میدهیم.
اما کار در ترمودینامیک بیشتر به کار انجام شده در اثر انبساط یا تراکم گاز، مرتبط میشود.
کار انجام شده توسط گاز
گازها میتوانند از طریق انبساط با تراکم، در مقابل فشار خارجی کار انجام دهند. کاری که توسط گاز انجام میشود را در برخی موارد به صورت کار فشار-حجم یا کار PV تعریف میکنند. گاز موجود در یک پیستون را در نظر بگیرید. اگر گاز حرارت ببیند، به مولکولهای آن انرژی اضافه خواهد شد. با اندازهگیری مقدار افزایش دمای گاز، افزایش انرژی جنبشی متوسط مولکولها قابل بررسی خواهد بود. با توجه به اینکه در این شرایط، گازها سریعتر حرکت میکنند، با دیواره پیستون نیز برخوردهای بیشتری خواهند داشت. این افزایش برخورد موجب انتقال انرژی به پیستون و حرکت دادن آن بر خلاف نیروی خارجی و افزایش حجم کلی گاز میشود. در این مثال، گاز بر روی محیط، کار انجام داده است.
برای محاسبه میزان کار انجام شده توسط گاز در مقابل فشار ثابت خارجی، تغییراتی در رابطه قبل باید انجام دهیم:
$$\begin{equation} \mathrm { w } = - \mathrm { P } _ {\text {external } } \times \Delta \mathrm { V } \end {equation}$$
- $$\mathrm { P } _ {\text {external }}$$: فشار خارجی
- $$\Delta \mathrm { V }$$: تغییر در حجم گاز. این تغییر را میتوان از طریق اختلاف حجم نهایی و حجم اولیه محاسبه کرد.
علامت کار در ترمودینامیک
زمانی که سیستم بر روی محیط، کار انجام دهد، کار منفی خواهیم داشت. مفهوم علامت کار در ترمودینامیک را به طور خلاصه میتوان به شکل زیر بیان کرد:
- زمانی که گاز کار انجام دهد، حجم گاز افزایش پیدا میکند و علامت کار انجام شده، منفی است.
- زمانی که بر روی گاز کار انجام شود، حجم گاز کاهش مییابد و علامت کار، مثبت خواهد بود.
مثال کار انجام شده توسط گاز
در ادامه قصد داریم تا با تعریفی ساده، محاسبات کار در ترمودینامیک را پی بگیریم. برای نشان دادن نحوه استفاده از رابطه بالا، یک تلمبه را در نظر بگیرید. فرض میکنیم که گاز موجود در تلمبه، نوعی گاز ایدهآل باشد. با فشردن تلمبه، روی هوا، کار انجام دادهایم. در ابتدا، حجم گاز برابر با ۳ لیتر است. برای اینکه حجم تلمبه به میزان 2/5 لیتر برسد، فشار خارجی برابر با 1/10 اتمسفر به آن وارد میکنیم. مقدار کار انجام شده را محاسبه کنید.
$$\begin {equation} \begin {aligned}
\mathrm { w } & = - \mathrm{ P } _ { \text {external }} \times \Delta \mathrm { V } \\
& = - \mathrm { P } _ {\text {external } } \times \left ( \mathrm { V } _ { \text {final} } - \mathrm { V } _ {\text {initial } } \right )
\end {aligned} \end {equation}$$
با اعمال مقادیر فشار خارجی، حجم نهایی و حجم اولیه در روابط بالا، مقدار کار محاسبه خواهد شد:
$$\begin {equation} \begin {aligned}
\mathrm { w } & = -1.10 \mathrm { a t m } \times ( 2 .50 \mathrm { L } - 3.00 \mathrm { L } ) \\
& = -1.10 \mathrm { atm } \times-0.50 \mathrm { L } \\
&=0.55 \mathrm { L } \cdot \mathrm { atm}
\end {aligned} \end {equation}$$
حال بهتر است علامت کار را بررسی کنیم. میدانیم که بر روی گاز کار انجام شده زیرا حجم گاز کاهش پیدا کرده است. این امر بدان معناست که کاری که انجام دادهایم باید علامت مثبت داشته باشد. بنابراین، محاسبات ما صحیح بوده است. همچنین به کمک ضریب تبدیل زیر، کار انجام شده به واحد ژول قابل تبدیل خواهد بود:
$$\begin {equation} \mathrm { w } = 0.55 \mathrm { L } . \mathrm {atm} \times \frac {101.325 \mathrm { J } } { 1 \mathrm { L }. \mathrm { atm } } = 56 \mathrm { J } \end {equation}$$
در نتیجه، برای اینکه حجم از ۳ لیتر به 2/5 لیتر کاهش پیدا کند، میزان ۵۶ ژول کار انجام دادهایم.
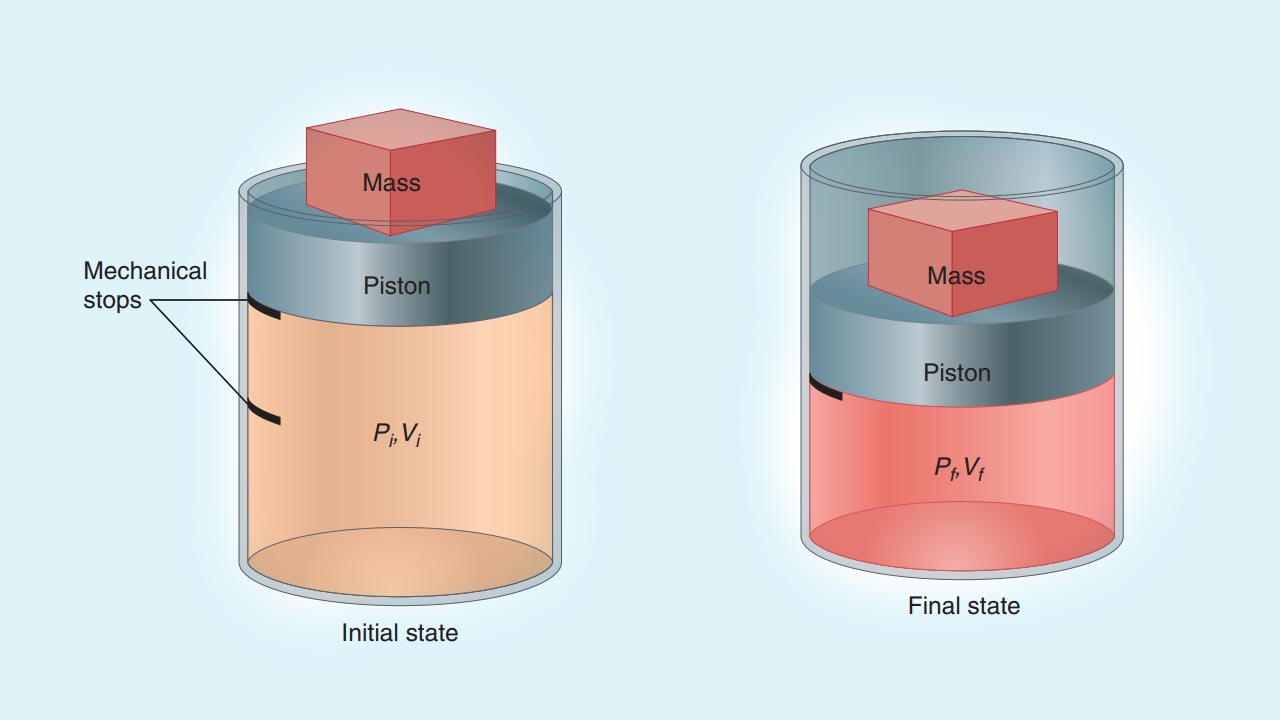
کار در ترمودینامیک در فرآیندهای هم حجم یا هم فشار
تحت شرایط مختلف، ممکن است بخواهیم کار را به هنگام ثابت بودن حجم یا فشار نیز محاسبه کنیم. در ادامه قصد داریم تا این شرایط را بررسی کنیم.
ثابت بودن حجم
در مواقعی، واکنشهایی وجود دارند که در محفظههای محکم و سربسته انجام میشوند که این مورد را میتوان در دستگاههای گرماسنج (کالریمتر) مشاهده کرد. در چنین واکنشهایی که تغییر حجمی نداریم $$(\Delta \mathrm { V } = 0)$$، گاز نمیتواند کاری بر روی سیستم انجام دهد و مقدار کار برابر با صفر خواهد بود و تغییرات انرژی در سیستم باید از راههای دیگری همچون گرما انجام شود.
ثابت بودن فشار
در شیمی معمولا تغییرات انرژی را مد نظر داریم که به هنگام انجام یک واکنش شیمیایی در فشار ثابت انجام میشوند. به طور مثال، انجام واکنش در داخل یک بشر، چنین شرایطی را ایجاد میکند چراکه فشار در سیستم با فشار اتمسفری محیط برابر است. در چنین شرایطی، حجم سیستم در طول واکنش ممکن است تغییر کند. درنتیجه، تغییرات حجم و به دنبال آن، انجام کار خواهیم داشت. گرما نیز میتواند بین سیستم (واکنش) و محیط منتقل شود. بنابراین به هنگام در نظر گرفتن تغییرات انرژی در واکنش، باید کار و گرما نیز لحاظ شوند. زمانی که در اثر واکنش، گاز تولید یا مصرف شود، سهم کار در تغییر انرژی بسیار مهم خواهد بود خاصه اگر تغییرات زیادی در تعداد مولهای گاز بین فرآوردهها و واکنشدهندهها داشته باشیم.
سایر فرآیندهای شیمیایی، با تغییرات کم در حجم رخ میدهند. از آنجمله میتوان به تغییرات فاز از مایع به جامد اشاره کرد. در این شرایط، تغییرات انرژی بر اثر کار نیز مقدار کمی را شامل میشوند حتی ممکن است به هنگام محاسبات، از آن صرف نظر شود. روابط بین کار، گرما و ثابت شکلهای انتقال انرژی، در قانون اول ترمودینامیک به خوبی مطرح شدهاند.

تعریف کار در ترمودینامیک به صورت دقیقتر
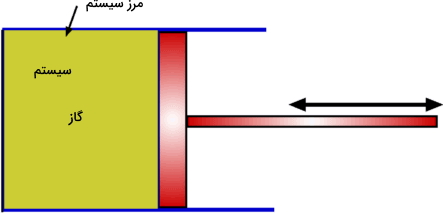
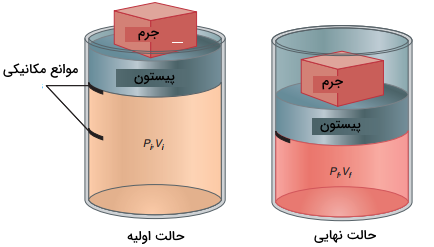
برای اینکه کار در ترمودینامیک را به طور دقیقتر و از منظر مهندسی بررسی کنیم، مثال دیگری را ارائه میکنیم. گاز محبوس شدهای را در یک سیلندر و پیستون همانند تصویر زیر در نظر بگیرید. در این مثال، سیستم را به تنهایی و به صورت گاز تعریف میکنیم. هرآنچه که به جز گاز در این تصویر قرار دارد، محیط خوانده میشود. با تراکم گاز، ارتفاع جرم در محیط کاهش پیدا میکند و سبب بوجود آمدن حجمهای اولیه و نهایی در سیستم میشوند که این حجمها با خط در تصویر نشان داده شدهاند.
شاخصههای مختلفی برای کار بیان میشوند که در ادامه به آنها اشاره میکنیم:
- کار نوعی حالت گذرا دارد به این معنی که فقط به هنگام یک تغییر در حالت سیستم و محیط دیده ظاهر میشود. تنها انرژی است که با حالتهای نهایی و اولیه سیستم همراه است.
- بر طبق قانون اول ترمودینامیک، اثر خالص کار، بر روی تغییر $$U$$ در سیستم و محیط متمرکز میشود. اگر تنها تغییر سیستم، ناشی از نیرو و جابجایی آن باشد (همانند مثال بالا)، کار بین سیستم و محیط جریان پیدا کرده است. کار را میتوان به صورت یک جرم در محیط نشان داد که توسط میدان گرانشی زمین، به بالا یا پایین میرود.
- مقدار کار را میتوان بر اساس رابطه زیر محاسبه کرد:
$$\begin {equation} w = \int _ { x _ { i } } ^ { x _ { f } } \mathbf { F } \cdot d \mathbf { x } \end {equation}$$
توجه داشته باشید که با توجه به اینکه در داخل انتگرال، ضرب داخلی داریم، تنها زمانی مقدار کار برابر با صفر نیست که برداری در جهت حرکت داشته باشیم.
- علامت کار را با محاسبه مقدار انتگرال میتوان درک کرد. اگر علامت کار مثبت باشد، در یک فرآیند آدیاباتیک، تغییرات انرژی درونی $$\Delta U$$ نیز مثبت خواهد بود. به طور معمول میتوان به این شکل بیان کرد که اگر $$w$$ مثبت باشد، محیط بر روی سیستم کار انجام داد است. اگر $$w$$ منفی باشد، سیستم بر روی محیط کار انجام داده است. مقدار کار انجام شده را همچنین میتوان به کمک تغییر انرژی پتانسیل جرم موجود در محیط نیز محاسبه کرد و رابطه آن به صورت زیر خواهد بود که در این رابطه، $$g$$ شتاب جاذبه و $$h$$، تغییر ارتفاع جرم $$m$$ خواهد بود:
$$\Delta E = m g \Delta h = - w$$
همانطور که میدانید، فشار را به صورت نیرو بر واحد سطح تعریف میکنند. با استفاده از این تعریف، کار انجام شده به هنگام جابجایی جرم، با روابط زیر قابل محاسبه خواهد بود:
$$\begin {equation} w = \int _ { x _ { i } } ^ { x _ { f } } \mathbf { F } \cdot d \mathbf { x } = - \int _ { x _ { i } } ^ { x _ { f } } P _ { \text {external} } A d x = - \int _ { V _ { i } } ^{ V _ { f } } P _ { \text {external} } d V \end {equation}$$
علامت منفی در رابطه بالا به این دلیل ظاهر میشود زیرا $$F$$ و $$dx$$، بردارهای در خلاف جهت یکدیگر هستند. توجه داشته باشید فشاری که در رابطه بالا آمده، فشار خارجی است که لزومی ندارد با فشار سیستم (P) برابر باشد.
کار الکتریکی
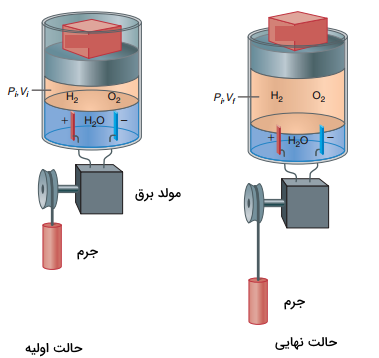
تصویر زیر، مثال مهم دیگری برای کار در ترمودنامیک یعنی کار الکتریکی را نشان میدهد. در این مثال، سیستم، محتویات داخل سیلندر است. جریان الکتریکی از طریق محلول هادی الکتریستیه و آب جریان پیدا میکند تا از طریق الکترولیز، گازهای اکسیژن و هیدروژن تولید شوند. این جریان میتواند به کمک یک مولد برق همچون دینام دوچرخه به هنگام رکاب زدن ایجاد شود. برای ایجاد جریان، جرم (مانند پا به هنگام پدال زدن)، باید به پایین حرکت کند. در این شرایط، محیط بر روی سیستم، کار الکتریکی انجام میدهد. در نتیجه این کار، مقداری از آب، به گاز هیدروژن و اکسیژن تبدیل میشود. کاری که برای انتقال بار $$Q$$ از طریق اختلاف پتانسیل الکتریکی $$\phi$$ انجام میشود عبارتست از:
$$\begin {equation} w _ {\text {electrical} } = Q \phi \end {equation}$$
با توجه به رابطه $$Q = I t$$ خواهیم داشت:
$$\begin {equation} w _ {\text {electrical} } =I \phi t \end {equation}$$
همچنین، سیستم از طریق افزایش حجم فاز گاز در فشار خارجی ثابت $$(P_ i)$$ بر روی محیط، کار انجام میدهد. این انجام کار، با بالا رفتن جرم روی پیستون نمایش داده میشود. بنابراین، کل کار انجام شده به صورت زیر تعریف میشود:
$$\begin {equation} w = w _ { P - V } + w _ { \text {elecrrical } } = I \phi t - \int _ { V _ { i } } ^ { V _ { f } } P _ { \text {external} } d V = I \phi t - P _ {\text {external} } \left ( V _ { f } - V _ { i } \right ) \end {equation}$$
شکلهای دیگر کار در ترمودینامیک
شکلهای دیگری از کار در ترمودینامیک وجود دارند که از آنجمله میتوان به کار انبساط سطح در برابر کشش سطحی اشاره کرد که حباب صابون، نمونهای از آن است. در جدول زیر، چهار نوع متفاوت از کار در ترمودینامیک نشان داده شدهاند. تمامی این موارد، به یک دیواره برای جداسازی سیستم از محیط نیاز دارند که در سه مورد ابتدایی این جدول، این دیوارهها باید متحرک باشند اما در کار الکتریکی، نیاز داریم تا دیواره، هادی الکتریسیته باشد.
| نوع کار در ترمودینامیک | متغیرها | رابطه و واحدهای معمول |
| انبساط حجم | فشار، حجم | $$\begin {equation} w = - \int _ { V _ { i } } ^ { V _ { f } } P _ { \text {external} } d V \quad \mathrm { P a } \mathrm { m } ^ { 3} = \mathrm { J } \end {equation}$$ |
| کشش | نیرو، طول | $$\begin {equation} w = \int _ { x _{ i } } ^ { x _ { f } } \mathbf { F } \cdot d \mathbf { l } \quad \mathrm { N } \mathrm { m } = \mathrm { J } \end {equation}$$ |
| انبساط سطح | کشش سطحی $$\gamma$$، مساحت | $$\begin {equation} w = \int _ {\sigma _ { i } } ^ {\sigma _ { f } } \gamma \cdot d \boldsymbol {\sigma} \quad\left (\mathrm { N } \mathrm { m } ^ { - 1 } \right) \left ( \mathrm { m } ^ { 2 } \right ) = \mathrm { J } \end {equation}$$ |
| الکتریکی | پتانسیل الکتریکی، بار الکتریکی | $$\begin{equation} w = \int _ { 0 } ^ { Q } \phi d Q ^ {} \quad \quad \mathrm { V } \mathrm{C}= \mathrm { J } \end {equation}$$ |
حل مثال از کار در ترمودینامیک
در ادامه به کمک چندین مثال حل شده، روابط مطرح شده در بالا را بکار میگیریم.
مثال محاسبه کار در ترمودینامیک بر اثر انبساط گاز
مقدار کار به هنگام انبساط ۲۰ لیتر از یک گاز ایدهآل را تا حجم ۸۵ لیتر در برابر فشار خارجی ۲/۵ بار حساب کنید.
$$\begin {equation} \begin {aligned}
w & = - \int _ { V _ { i } } ^ { V _ { f } } P _ { \text {external } } d V = - P _ {\text {external } } \left ( V _ { f } - V _ { i } \right) \\
& = - 2.50 \mathrm { bar} \times \frac { 1 0 ^ { 5 } \mathrm { P a } } { \mathrm { bar } } \times ( 85.0 \mathrm { L } - 20.0 \mathrm { L } ) \times \frac {10 ^ { - 3 } \mathrm { m } ^ { 3 } } { \mathrm { L } }= -16.3 \mathrm { k J }
\end {aligned} \end {equation}$$
مثال کار در ترمودینامیک ناشی از انبساط سطح
حباب هوا در یک مایع، از شعاع ۱ سانتیمتر به شعاع ۳/۲۵ سانتیمتر، منبسط میشود. کشش سطحی آب برابر با $$71.99 N m ^ { - 1 }$$ است. چه مقدار کار برای افزایش مساحت حباب انجام شده است؟ محتوای حباب را به عنوان سیستم در نظر بگیرید.
برای حل این سوال، ضریب ۲ را در محاسبات لحاظ کردهایم زیرا حباب، یک سطح داخلی و یک سطح خارجی دارد. همانطور که در سوال مطرح شده، حباب و محتوای آنرا به عنوان سیستم در نظر میگیریم. بردارهای $$\gamma$$ و $$\sigma$$، خلاف جهت یکدیگر قرار دارند که علامت منفی در انتگرال دوم را سبب میشوند.
$$\begin{equation}\begin{aligned}
w &=\int_{\sigma_{i}}^{\sigma_{f}} \gamma \cdot d \boldsymbol {\sigma} = -\int _ { \sigma _ { i } } ^ { \sigma _ { f } } \gamma d \sigma = 2 \gamma 4 \pi\left ( r _ { f } ^ { 2 } - r _ { i } ^ { 2} \right) \\
& = - 4 \pi \times 71.99 \mathrm { N m } ^ { - 1 } \ \left ( 3 .25 ^ { 2 } \mathrm { c m } ^ { 2 } - 1.00 ^ { 2 } \mathrm { cm } ^ { 2 }\right) \times \frac { 1 0 ^ { - 4 } \mathrm { m } ^ { 2 } }{ \mathrm { c m } ^ { 2 }} \\
& = -0.865 \mathrm { J }
\end {aligned} \end {equation}$$

مثال کار الکتریکی
جریانی با شدت ۳/۲ آمپر از میان یک المنت حرارتی به مدت ۳۰ ثانیه عبور میکند. پتانسیل الکتریکی برابر با ۱۴/۵ ولت است. کار انجام شده بر روی المنت را محاسبه کنید.
$$\begin {equation} w = \int _ { 0 } ^ { Q } \phi d Q ^ { } = \phi Q = I \phi t = 14.5 \mathrm { V } \times 3.20 \mathrm { A } \times 30.0 \mathrm { s } = 1.39 \mathrm { k J } \end {equation}$$
مثال کار کشش
اگر نیروی مورد نیاز برای کشیدن یک بافت به میزان $$x$$، برابر با $$F = - k x$$ باشد، مقدار کار انجام شده برای کشیدن بافت به میزان ۰/۱۵ سانتیمتر را محاسبه کنید. $$k = 100 N m ^ { -1 }$$
برای حل این سوال باید بین نیروی مقاوم F در بافت و نیروی $$F \prime$$، یعنی نیرویی که توسط شخص برای کشیدن پارچه اعمال میشود تفاوت قائل شد. این دو نیرو با رابطه زیر به یکدیگر مرتبط میشوند:
$$F = - F ^ \prime$$
$$\begin {equation} w = \int \mathbf { F } ^ { \prime } \cdot d \mathbf { l } = \int _ { x _ { 0 } } ^ { x _ { f } } k x d x = \left [ \frac { k x ^ { 2 } } { 2 } \right ] _ { x _ { 0 } } ^ { x _ { f } } = \left [ \frac{100 . \mathrm { N } \mathrm { m } ^ { - 1 } \times x ^ { 2 } } { 2 } \right ] _ { 0 } ^ { 0 . 1 5 } = 1.1 \mathrm { J } \end {equation}$$
اگر این مطلب برای شما مفید بوده است، آموزشها و مطالب زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس شیمی
- مجموعه آموزشهای مهندسی شیمی
- آموزش ترمودینامیک مهندسی شیمی
- انرژی آزاد هلمهولتز — به زبان ساده
- فرآیندهای ترمودینامیکی — به زبان ساده
^^










فرمول _P دلتا V رو می شه واسه فرآیند هم حجم هم استفاده کرد یا فقط متعلق به فرآیند هم فشار هست؟؟؟؟