سینماتیک سیالات — مقدمه‌ای بر مکانیک

سینماتیک سیالات حرکت سیال را بدون در نظر گرفتن نیروهای وارد شده به آن مورد بررسی قرار می‌دهد. در این مطلب قصد داریم تا در مورد مفاهیمی هم‌چون مشتق مادی، توصیف لاگرانژی حرکت سیال و بیان اویلری این حرکت صحبت کنیم.

توصیف لاگرانژی و اویلری از حرکت سیال

در حالت کلی، مبحث سینماتیک به تحلیل و بررسی حرکت هر نوع ماده‌ای می‌‌پردازد.

فیلم آموزش هیدرودینامیک در فرادرس

کلیک کنید

در مکانیک سیالات این مبحث مختص سیالات است. از نظر بنیادی دو دیدگاه متفاوت به منظور توصیف حرکت وجود دارد. ابتدایی‌ترین روش، بیانی است که در دبیرستان با آن آشنا شده‌اید. این بیان می‌گوید که به منظور توصیف حرکت هر ذره‌ای، مسیر آن را دنبال کنید.

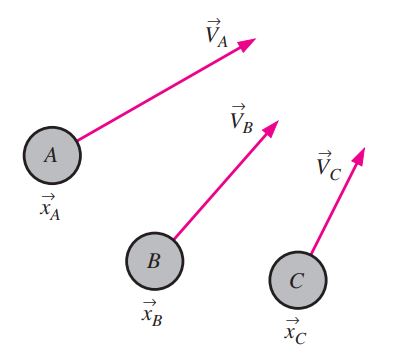
ممکن است تجربه بازی بیلیارد یا فوتبال را داشته باشید؛ در تمامی این موارد، حرکت توپ‌ها با استفاده از قوانین نیوتن قابل توصیف هستند. با به‌کارگیری این قوانین می‌توان جهت و مسیر دقیق حرکت اجسام را توصیف کرد. سینماتیک چنین ذراتی با استفاده از بردارهای مکان ... و x_B و x_A و بردارهای سرعت ... , V_A ,V_B قابل توصیف هستند. «روش لاگرانژی» (Lagrangian Description) یعنی این‌که با دنبال کردن هر ذره از سیستم، تمامی مجموعه را تحلیل کنیم. این بیان، مفهومی است که در ترمودینامیک نیز با آن آشنا هستید. نوع نگاه انتخاب شده در تحلیل جریان توربولانس بسیار کمک کننده است.

همان‌طور که احتمالا می‌دانید توصیف حرکت ذرات سیال بسیار مشکل‌تر از تحلیل برخورد توپ‌های بیلیارد خواهد بود. دلیل اول شناسایی کردن دقیق ذرات سیال و دلیل دوم پیوسته بودن محیط آن است.

از دیدگاه میکروسکوپی یک سیال متشکل از میلیون‌ها مولکول است که همانند توپ‌های بیلیارد مرتباً با یکدیگر برخورد دارند. پس احتمالا می‌توان با مدل‌سازی تمامی این مولکول‌ها نیز، حرکت سیال را پیش‌بینی کرد. این استدلال روی کاغذ درست است اما دقت کنید که با سریع‌ترین کامپیوتر‌هایی که بشر تاکنون ساخته، نمی‌توان این مدل‌سازی را انجام داد. بنابراین بهتر است کمی خلاق‌تر باشیم و با استفاده از روشی جایگزین این مدل‌سازی را انجام دهیم.

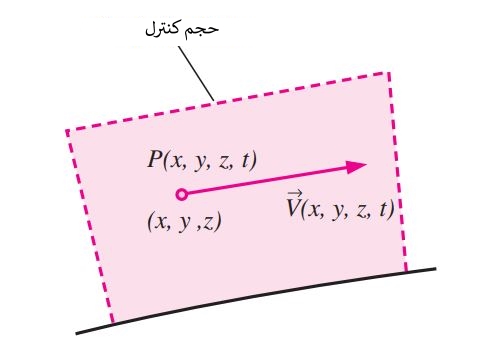
مرسوم‌ترین توصیف به منظور مدل‌سازی سیال، «بیان اویلری» (Eulerian Description) است. در این روش حجم محدودی تحت عنوان «محدوده سیال» (Flow Domain) یا «حجم کنترل» (Control Volume) که سیال در آن جریان دارد، مورد مطالعه قرار می‌گیرد. همچنین به‌جای دنبال کردن ذرات سیال، متغیرهایی میدانی تعریف می‌شوند و این متغیرها در محدوده سیال مورد بررسی قرار می‌گیرند.

این میدان‌ها می‌توانند به صورت برداری یا اسکالر باشند. میدان سرعت که در معادله زیر بیان شده، به صورت برداری است.

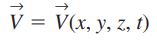
به همین صورت می‌توان میدان شتاب، جرم و یا هر متغیر دیگری را تعریف کرد. تمامی این میدان‌ها با هم می‌توانند سیال را توصیف کنند. به عنوان مثال میدان سرعتی برای یک سیال تراکم ناپذیر، دوبعدی و پایا به صورت زیر تعریف شده. در ادامه برای درک بهتر موضوع و به صورت زیر نقاطی که در آن سرعت سیال صفر است، تعیین می‌شوند.

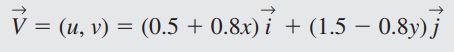
این میدان سرعت در واقع بیانی اویلری از وضعیت سیال است. نقطه سکون (Stagnation Point)، مکانی است که در آن تمامی مولفه‌های سرعت صفر باشند. بنا‌براین می‌توان گفت:

درنتیجه نقاط x و y بدست آمده، نقاطی هستند که در آن سرعت سیال صفر است. اگر بخواهیم با توجه به این معادله سرعت سیال را در نقطه مشخصی بیابیم، می‌توانیم با جایگذاری مختصات نقطه در معادله، سرعت سیال را در آن مکان به دست آوریم.

میدان شتاب

همان‌طور که در مفاهیم ترمودینامیک نیز بیان شده، (با توجه به قوانین اول و دوم ترمودینامیک) می‌توان مجموعه‌ای از  خاصیت‌ها را برای یک سیستم بسته تعریف کرد. همین استدلال نیز در بیان مفاهیم لاگرانژی و اویلری میدان‌های سرعت در سیال وجود دارد. در این‌جا به جای سیستم بسته، از ذره‌ای از سیال به عنوان سیستم استفاده می‌کنیم.

فیلم آموزش مکانیک سیالات ۱ در فرادرس

کلیک کنید

به عنوان مثال می‌توان مکان هر ذره را با استفاده از برداری مادی ((x_particle(t), y_particle(t),  z_particle(t) توصیف کرد. اما دقت کنید که به تعدادی اعمال ریاضی به منظور توصیف معادله حرکت در قالب بیان اویلری نیازمند هستیم. برای نمونه قانون دوم نیوتن را در نظر بگیرید که برای ذره‌ای از یک سیال اعمال شده است.

در این معادله F نیروی خالص وارد شده به ذره سیال، m جرم این ذره و a شتاب آن است. با استفاده از تعریف می‌دانیم که شتاب این ذره، مشتق مادی سرعت آن نسبت به زمان است. بنابراین می‌توان نتیجه گرفت:

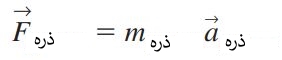
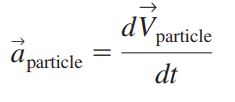
هم‌چنین می‌توان گفت که در زمان t، سرعت ذره سیال همان سرعتی است که توسط میدان سرعت در نقطه (x,y,z) بیان شده. به منظور مشتق‌گیری از میدان سرعت می‌توان از قانون مشتق‌گیری زنجیره‌ای به صورت زیر استفاده کرد. از آنجایی که متغیر V وابسته به چهار متغیر مستقل (x,y,z,t) است بنابراین می‌توان نوشت:

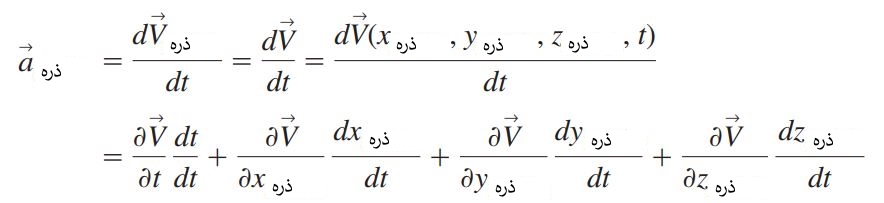
در این رابطه، ∂ اوپراتور مشتق جزئی و d اوپراتور مشتق کامل است. دقت کنید که مکان مادی هر ذره در بیان لاگرانژی برابر است با (r(x_particle, y_particle, z_particle که در بیان اویلری معادل با بردار مکان ($$\overrightarrow{x}$$,$$\overrightarrow{y}$$,$$\overrightarrow{z}$$) است. بنابراین معادله بالا به عبارت زیر تبدیل خواهد شد.

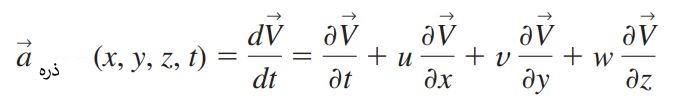
توجه داشته باشید که عبارت بالا را می‌توان به صورت زیر، در قالب متغیرهای میدانی نوشت.

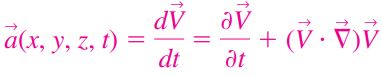
در این رابطه ∇، اوپراتور گرادیان است که به صورت زیر تعریف می‌شود.

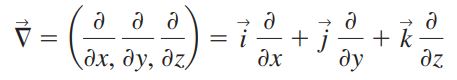
در مختصات کارتزینی نیز مولفه‌های شتاب به صورت زیر بیان می‎‌شوند.

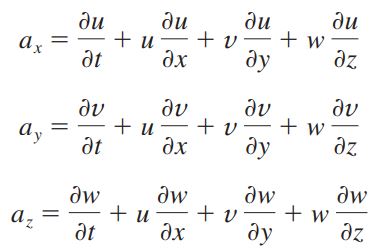
خطوط جریان

یک خط جریان منحنی است که همواره مماس بر بردار سرعت قرار دارد. با استفاده از تحلیل خطوط جریان می‌توان جهت حرکت ذره‌های سیال را شناسایی نمود. بر مبنای ریاضیات می‌توان به منظور توصیف خطوط جریان به عباراتی دست یافت.

فیلم آموزش مکانیک سیالات – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

در ابتدا بردار جابجایی d$$\overrightarrow{r}$$=d$$\overrightarrow{x}$$i+d$$\overrightarrow{y}$$j+d$$\overrightarrow{z}$$k را در نظر بگیرید. از آن‌جایی که این خط جریان مماس بر بردار سرعت است و با فرض این که بردار V برابر است با: u_i+v_j+w_k، می‌توان نوشت:

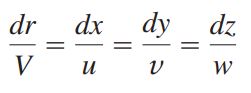
بنابراین معادله خطوط جریان در دستگاه x-y، به صورت زیر است.

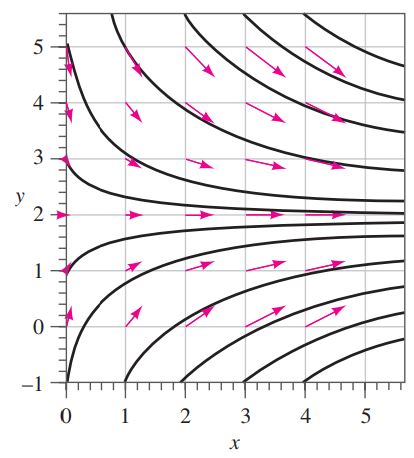
این معادله در بعضی موارد به صورت عددی و گاهی نیز به صورت تحلیلی قابل حل خواهد بود. به عنوان مثال معادله خطوط جریان مربوط به معادله زیر، در شکل 1 نشان داده شده است. این خطوط جریان را می‌توان به صورت زیر محاسبه کرد.

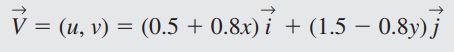
با استفاده از معادله فرض شده، خواهیم داشت:

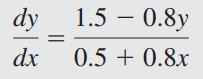
پس از انتگرال گیری از معادله بالا می‌توان مسیرخطوط جریان را محاسبه کرد.

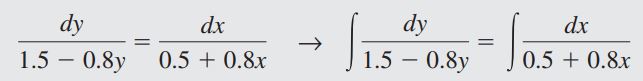
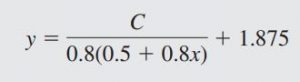
دقت کنید همان‌طور که در شکل پایین نیز دیده می‌شود، به ازای هر مقداری از C، یک خط جریان خواهیم داشت. همچنین توجه داشته باشید که این خطوط جریان، هیچ‌گاه همدیگر را قطع نخواهند کرد.

در صورتی که به مباحث مرتبط در زمینه مهندسی مکانیک علاقه‌مند هستید، احتمالا مطالب زیر می‌تواند برایتان مفید باشد:

• تابع جریان در سیالات — به زبان ساده
• ترمودینامیک — از صفر تا صد
• فشار چیست و مروری بر روش‌های اندازه‌گیری آن
• استاتیک سیالات
• جریان توربولانس -- به زبان ساده

^^