روابط مثلثاتی و فرمول های مثلثاتی مهم + دانلود PDF خلاصه رایگان
هندسه و روابط هندسی بخصوص در مثلثها، باعث رشد علوم ریاضی در دنیایی واقعی و زندگی روزمره ما شده است. مثلث یکی از شکلهای پایه محسوب شده در نتیجه روابطی که در مثلثها وجود دارد، از اهمیت زیادی برخوردار هستند. هر مربع را میتوان به دو مثلث شکست. مستطیل نیز براساس دو مثلث چسبیده به هم، قابل نمایش است. چندضلعیها هم از پیوند چندین مثلث بدست میآیند. بنابراین دایره و مثلث را میتوان از اصلیترین اشکال هندسی در نظر گرفت. در این متن میخواهیم به کمک یک دایره و نوع خاصی از مثلث، روابط مثلثاتی یا فرمول های مثلثاتی و روابط مهم بین آنها را بیان کرده و با ذکر مثالهایی، اطلاعاتمان را در مورد این نسبتها، افزایش دهیم.


اگر لازم است در مورد مورد مثلث و فرمهای مختلف آن و همچنین مبانی هندسی، اطلاعاتی کسب کنید، مراجعه به مطالب مثلث چیست ؟ — به زبان ساده و دایره چیست ؟ — تعریف و مفاهیم به زبان ساده از مجله فرادرس مفید خواهد بود. همچنین خواندن نوشتارهای سینوس، کسینوس و تانژانت یک زاویه — به زبان ساده و تانژانت و کتانژانت — نسبتهای مثلثاتی به زبان ساده نیز خالی از لطف نیست.
روابط مثلثاتی و فرمولهای مثلثات
در ریاضیات، هندسه با خط و نقطه آغاز میشود. مفهوم نقطه را در نظر بگیرید. خط نیز مفهومی است که براساس آن میتوان دو نقطه را به یکدیگر وصل کرد. از طرفی در هندسه اقلیدسی (هندسه مسطحه)، کوتاهترین فاصله بین دو نقطه، یک خط راست است.
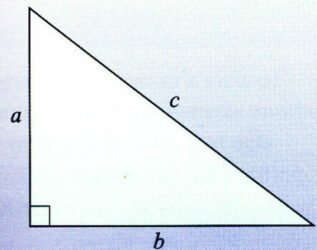
به این ترتیب به کمک خط راست شکلهای مختلف پدید آمده که مهمترین آنها، مثلث (Triangle) یا سه گوش است. در تصویر زیر یک مثلث را مشاهده میکنید.

در روابط مثلثاتی به یک مثلث خاص نیاز داریم. به یک مثلث با زاویه راستگوشه، گونیا یا «قائمه» (Right Angle) متمرکز میشویم. مشخص است که اگر یک زاویه یا گوشه از مثلثی قائمه (راست) باشد، به آن «مثلث قائمالزاویه» (Right-angled Triangle) یا «مثلث راست گوشه» گفته میشود. این مثلث از آن جهت مهم است که قضیه فیثاغورس (Pythagorean theorem) ( یا به شکل دیگر رابطه فیثاغورث) در مورد اضلاع یا بَرهای آن صادق است.
در یک مثلث قائمالزاویه، ضلعی که روبروی زاویه عمود قرار گرفته، «وتر» (Hypotenuse) نامیده میشود. در چنین مثلثی، وتر از دو ضلع دیگر مثلث بزرگتر است. این دو ضلع را گاهی ساقهای مثلث نیز مینامند.
به این ترتیب اگر ضلع یا بَرهای مثلث «راست گوشه» (قائم الزاویه) را با نامهای a,b,c مشخص کنیم بطوری که c وتر باشد، رابطه زیر نشانگر رابطه فیثاغورس در مورد اضلاع مثلث قائمالزاویه خواهد بود.
به تصویر زیر دقت کنید. یک مثلث راست گوشه به همراه رابطه یا قضیه فیثاغورس در آن دیده میشود.
شاخهای از هندسه که به بررسی نسبتها بین ضلعهای چنین مثلثی میپردازد، مثلثات نامیده میشود. به همین دلیل چنین نسبتهایی را به نام نسبتهای مثلثاتی میشناسیم. خوشبختانه میتوان این نسبتها را براساس تابعی از زاویههای مثلث قائم الزاویه بیان کرد و برای هر یک از آنها اسامی ساخت. البته این کار در زمانهای گذشته صورت گرفته و برای مثال به فارسی قدیم (عربی)، عبارتهای ضل (سایه) یا جیب (ناحیه محصور) برای این گونه نسبتها به کار میرفته است.
در ادامه متن ابتدا به تاریخچه مختصری از نسبتهای مثلثاتی میپردازیم تا برای کسانی که کنجکاو و علاقمند به ریشه این شاخه از علم آشنا شوند، مطلب خواندنیتر شود.
تاریخچه
ستاره شناسان سومری با استفاده از تقسیم دایره به 360 درجه، اندازه گیری زاویه را مطالعه کردند. آنها و بعداً بابِلیها، نسبت ضلعهای مثلث مشابه را مطالعه کردند و برخی از خصوصیات این نسبتها را کشف کردند اما آن را به روشی منظم برای یافتن اضلاع و زاویههای مثلث تبدیل نکردند.
در قرن 3 قبل از میلاد ، ریاضیدانهایی مانند اقلیدس و ارشمیدس خواص زاویههای محاط در دایرهها را بررسی کرده و براساس آنها قضیههایی را ثابت کردند که معادل فرمولهای مثلثاتی مدرن و امروزی است. در قرن دوم میلادی، منجم یونانی-مصری بطلمیوس (از اسکندریه مصر) جداول مثلثاتی (جدول بطلمیوس) را در جلد اول، فصل 11 کتاب «آلماگست» (Almagest) خود را منتشر کرد. بطلمیوس برای تعریف توابع مثلثاتی خود از طول وتر استفاده کرد. قرنها بعد از رساله بطلمیوس، گذشت تا این محاسبات به روز شد و با دقت بیشتری منتشر گردید. در جهان بعد از قرون وسطا، تا قبل از حضور دانشمندان اسلامی و ایرانی، همچنان جدولهای بطلمیوس مورد استفاده قرار میگرفت.

در قرن دهم میلادی، ریاضیدانان اسلامی از هر شش تابع مثلثاتی (سینوس، کسینوس، تانژانت، کتانژانت، سکانت و کسکانت) استفاده میکردند و مقادیر آنها را جدولبندی کرده و از این مقادیر برای حل مسائل مربوط به هندسه مسطحه و کروی بهره میبردند.
چند شخصیت ایرانی نظیر «خواجه نصیرالدین طوسی» به عنوان خالق مثلثات مشهورند زیرا این شاخه از ریاضیات را تحت یک رشته جدید ریاضی عنوان کردند. خواجه نصیرالدین طوسی اولین کسی بود که مثلثات را به عنوان یک رشته ریاضی مستقل از نجوم در نظر گرفت و مثلثات کروی را به شکل امروزی آن بیان کرد. وی شش حالت مشخص مثلث قائم الزاویه را در مثلثات کروی برشمرد و در کتاب «در شکل بخش»، قانون سینوسها را برای مثلثهای صفحهای و کروی بیان کرد. همچنین قانون تانژانتهای مثلث کروی را کشف و اثباتی برای هر دو این قوانین ارائه داد.
مطالعه مثلثات در ریاضیات اسلامی، توسط ریاضیدانی مانند «خوارزمی» و «ابوالوفا» ادامه یافت. این شاخه از هندسه یک رشته مستقل در جهان اسلام شد. در قرن پانزدهم، «غیاثالدین جمشید كاشانی»، ریاضیدان محاسب و منجم ایرانی، اولین توصیف صریح قانون کسینوس را به شکلی مناسب برای مثلثات ارائه داد. در فرانسه، قانون کسینوس هنوز به عنوان قضیه «الکاشی» شناخته میشود. وی همچنین جداول مثلثاتی مقادیر تابع سینوس را به 8 رقم اعشار، برای زاویههایی با اختلاف 1 درجه را به شکل استدلالی ارائه داد.
ترجمه متون عربی و یونانی منجر به این شد که مثلثات در غرب از آغاز دوره رنسانس به عنوان یک موضوع علمی در نظر گرفته شود. توسعه مثلثات مدرن در دوران عصر روشنگری غربی با ریاضیات قرن هفدهم توسط «آیزاک نیوتن» (Isaac Newton) و «جیمز استرلینگ» (James Stirling) آغاز شد و با «لئونارد اویلر» (Leonhard Euler) به شکل مدرن خود رسید.

دانلود PDF روابط و فرمول های مثلثات
از جمله مواردی که بعد از آشنایی با مثلثات مطرح میشود، یادگیری روابط مثلثاتی و فرمولهای مربوط به آن است. به همین دلیل، «فرادرس» تقلبنامهای را برای روابط مثلثاتی تهیه و تدوین کرده که لینک دانلود فایل PDF آن در ادامه آورده شده است.
- برای دانلود PDF روابط و فرمولهای مثلثات + اینجا کلیک کنید.
دایره مثلثاتی
قبل از آنکه به نسبتهای مثلثاتی بپردازیم، باید با دایره مثلثاتی آشنا شویم. این یک دایره خاص است که شعاع آن یک واحد در نظر گرفته میشود. به این معنی که میتوان شعاع این دایره را یک سانتی متر یا صد متر در نظر گرفت. ولی مهم برای ما آن است که این طول (با هر واحد اندازهگیری) مبنا و معیار تلقی شده و براساس آن، اندازههای دیگر تعریف میشوند.
نکته: از آنجایی که نسبتهای مثلثاتی به صورت تقسیم یا کسری از اضلاع مثلث درون این دایره محاسبه میشوند، واحد اندازهگیری طول مهم نیست زیرا میدانیم که نسبتگیری یا تناسب، واحد اندازهگیری را از بین میبرد. از این جنبه این نسبتها مهم هستند که با بزرگ یا کوچک بودن دایره (تغییر شعاع آن)، این نسبتها تغییر نکرده و برای زاویههای یکسان، ثابت هستند. این موضوع در مورد «عدد پی» () نیز صادق است. به این معنی که نسبت محیط به قطر دایره همیشه برابر با عدد پی بوده و مقداری بدون واحد است.
در تصویر زیر یک دایره با شعاع واحد را مشاهده میکنید.
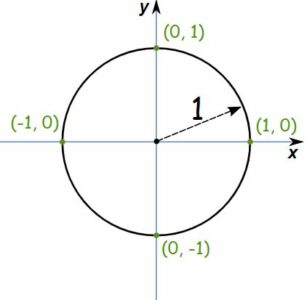
همانطور که به خوبی دیده میشود، مرکز این دایره در مبدا مختصات دکارتی قرار گرفته و شعاع آن واحد یا یک است. محور افقی و عمودی در این مختصات، دایره مثلثاتی را به چهار ناحیه متفاوت ولی با اندازههای یکسان تقسیم کردهاند.
واضح است که محل برخورد این دایره با محور افقی در قسمت مثبت محور در نقطه (1,0) و در بخش منفی، نقطه (1,0-) است. همچنین تقاطع محور عمودی با دایره مثلثاتی نیز در نقطههای (0,1) و (1-,0) اتفاق میافتد. این نقاط در ادامه متن مورد توجه قرار خواهند گرفت. این چهار ناحیه و نقاط طلاقی دایره مثلثاتی با محورهای مختصات را در تصویر زیر به خوبی مشخص کردهایم.
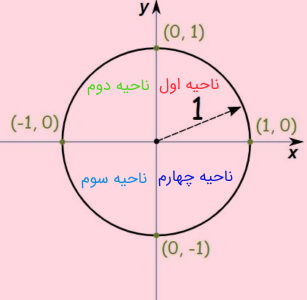
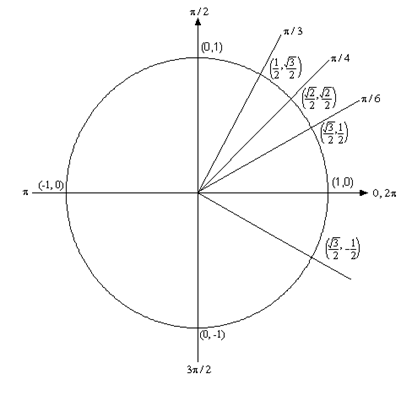
این بار به مختصات نقاطی توجه داریم که روی دایره مثلثاتی قرار داشته و علامتهای مربوط به طول و عرض این نقاط روی مختصات دکارتی را مشخص میکنیم. بخشها و علامت مقدار طول و عرض نقطهها مطابق با تصویر ۳ هستند.
نکته: از آنجایی که این نواحی از تقسیم دایره مثلثاتی به چهار بخش تشکیل شدهاند، به آنها گاهی ربع دایره مثلثاتی نیز گفته میشوند و از اصطلاح ربع اول، ربع دوم، ربع سوم یا ربع چهارم برای مشخص کردن آنها استفاده میکنند.
حال به بررسی نسبتهای مثلثاتی و نمایش یک مثلث قائمالزاویه در این دایره خواهیم پرداخت.
نسبت مثلثاتی و دایره مثلثاتی
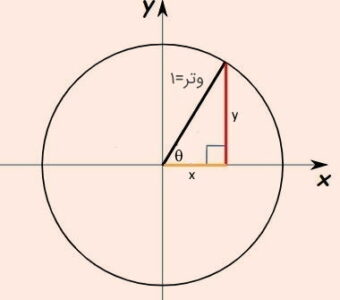
یک نقطه روی محیط دایره مثلثاتی را در نظر بگیرید و از آن نقطه، خطی عمود بر محور افقی ایجاد کنید. به کمک این نقطه یک مثلث ایجاد خواهیم کرد. گامهای زیر را برای این کار برمیداریم.
- گام یکم: پاره خطی از نقطه روی محیط دایره تا محور افقی ایجاد میکنیم. یک خط، یکی از ضلع مثلث مورد نظرمان را میسازد. طول این خط را y مینامیم.
- گام دوم: ضلع دیگر را به کمک محور افقی میسازیم. پاره خطی از مرکز مختصات تا محل برخورد خط قبلی روی محور افقی را در نظر بگیرید. واضح است که چون پاره خط اول بر محور افقی عمود است، بر پاره خط دوم نیز عمود خواهد بود. طول این خط را x مینامیم.
- گام سوم: در انتها از نقطه روی محیط دایره (نقطه اولیه)، پاره خطی به مرکز مختصات رسم میکنیم. به این ترتیب سه ضلع از یک مثلث قائمالزاویه ساخته میشود. این خط را «وتر» مثلث قائمالزاویه مینامیم.
این گام یا مراحل در تصویر زیر دیده میشود. همچنین زاویه قائمه یا عمود هم مشخص شده. طول خطوط ایجاد شده با توجه به محل انتخاب نقطه روی محیط دایره میتواند متفاوت باشد. ولی همیشه به یاد داشته باشید، خطی که از نقطه به مرکز مختصات متصل است، طولی برابر با ۱ دارد، زیرا شعاع دایره مثلثاتی را نشان میدهد.
به این ترتیب بین x ،y و وتر این مثلث قائمالزاویه، رابطه زیر، بنا به قضیه فیثاغورس، برقرار است.
زاویه حاصل از وتر با محور افقی را (بخوانید تِتا) مینامیم. این زاویه مبنای محاسبه نسبتهای مثلثاتی یک زاویه یا کمان روبروی آن در دایره مثلثاتی است. توجه داشته باشید که زاویه یا کمان را برحسب واحد رادیان میسنجیم. البته با تبدیل زاویه برحسب «رادیان» (Radian) به «درجه» (Degree) یا «گراد» (Grad) نیز میتوان نسبتهای مثلثاتی را بدست آورد.
نکته: اگر کمان دایره را به ۳۶۰ بخش مساوی تقسیم کنیم، زاویههای حاصل روی دایره مثلثاتی، یک درجه نامیده میشوند. اگر این کمان را به ۴۰۰ بخش تقسیم کرده باشیم، هر زاویه را یک گراد مینامیم. همچنین به کمانی از یک دایره که طولی برابر با شعاع آن داشته باشد، یک رایان گفته میشود. در نتیجه زاویه روبرو به چنین کمانی دارای اندازه زاویهای به اندازه یک رادیان است. البته مشخص است که رادیان برعکس درجه یا گراد، برای سجش طول کمانها به کار میرود ولی اغلب برای نمایش زاویه روبرو به چنین کمانی، از واحد رادیان استفاده میشود.
کسینوس زاویه
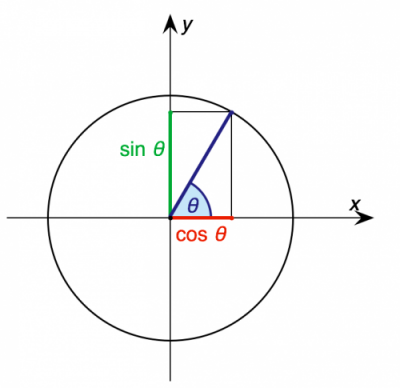
اولین نسبت مثلثاتی به کمک تقسیم یا نسبت x به طول وتر این مثلث ساخته میشود که «کسینوس» (Cosine) نام گرفته که با علامت نشان داده میشود. از آنجایی که طول وتر برابر با ۱ است، این نسبت همیشه با طول x برابر است. از طرفی چون این مثلث درون دایره مثلثاتی قرار گرفته، حداکثر مقدار x برابر با ۱ و حداقل آن نیز ۱- خواهد بود.
به این ترتیب میتوانیم مقدار کسینوس زاویه را به صورت زیر مشخص کنیم. واضح است که ضلع x، مجاور به زاویه است.
حال اگر بدون یک دایره مثلثاتی بخواهیم مقدار کسینوس زاویهای از یک مثلث قائمالزاویه را مشخص کنیم، میتوان گفت که کسینوس از تقسیم ضلع مجاور به زاویه به وتر مثلث قائمالزاویه حاصل میشود.
کسینوس زاویه برابر است با تقسیم اندازه ضلع مجاور زاویه بر طول وتر مثلث قائمالزاویه
سینوس زاویه
به همین ترتیب، مقدار «سینوس» (Sine) زاویه (که به صورت نشان داده میشود) به کمک تقسیم اندازه یا عرض نقطه روی دایره مثلثاتی به وتر حاصل میشود.
باز هم بدون در نظر گرفتن دایره مثلثاتی، میتوان سینوس یک زاویه مانند را براساس عبارت زیر بدست آورد.
سینوس زاویه برابر است با تقسیم اندازه ضلع مقابل زاویه به طول وتر مثلث قائمالزاویه
در تصویر زیر نسبتهای سینوس و کسینوس روی دایره مثلثاتی به خوبی دیده میشوند. همانطور که گفتیم، با توجه به واحد بودن شعاع دایره مثلثاتی، وتر مثلث قائمالزاویهای که درون آن قرار میگیرد، برابر با یک است.
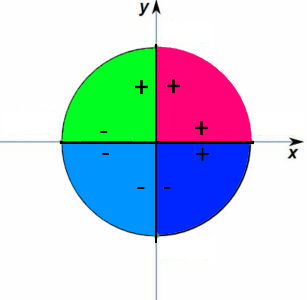
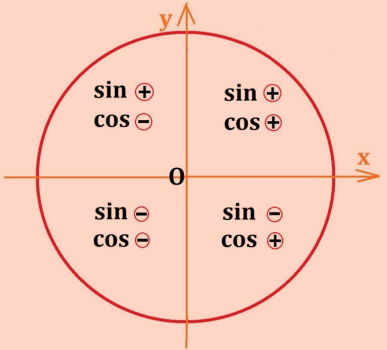
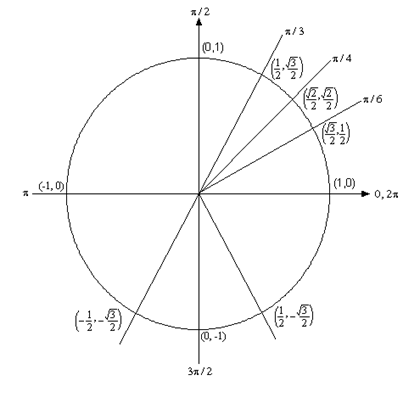
با توجه به محل قرارگیری زاویه در هر یک از ربعهای دایره مثلثاتی که در تصویر ۳ قابل مشاهده است، میتوان علامت هر یک از نسبتهای مثلثاتی سینوس و کسینوس را مشخص کرد. به تصویر زیر توجه کنید. همانطور که دیده میشود، علامت مقدار حاصل از محاسبه سینوس و کسینوس زاویه در ربع اول، مثبت است. در ربع دوم، علامت سینوس زاویه مثبت ولی کسینوس، منفی است. در ربع سوم هر دو نسبت مثلثاتی سینوس کسینوس دارای علامت منفی هستند. در مقابل در ربع چهار، نسبت مثلثاتی سینوس، منفی ولی کسینوس مثبت است.
با توجه به مثلث قائمالزاویه که در دایره مثلثاتی قرار دارد، میتوان روابط زیر را به کمک قضیه فیثاغورس نوشت.
از طرفی با توجه به قرارگیری زاویه روی یکی از محورها، به رابطههای زیر خواهیم رسید. البته توجه داشته باشید که در اینجا اعداد مربوط به زاویهها برحسب درجه است.
تانژانت زاویه
همانطور که گفتیم، نسبت مثلثاتی سینوس و کسینوس براساس تقسیم ضلع مقابل یا مجاور به زاویه بر وتر مثلث قائمالزاویه محاسبه میشوند. این بار ضلع روبرو با زاویه را بر ضلع مجاور به زاویه تقسیم میکنیم. باز هم دایره مثلثاتی در تصویر ۴ را در نظر بگیرید. اگر این تقسیم را به شکل زیر بنویسیم، تانژانت زاویه را محاسبه کردهایم.
توجه دارید که در مخرج کسرها به این علت ۱ ظاهر شده که طول وتر در دایره مثلثاتی برابر با یک است. در نتیجه تعریفی که برای تانژانت قابل ارائه است حاصل تقسیم سینوس زاویه بر کسینوس آن خواهد بود.
کتانژانت زاویه
این بار به نسبت ضلع مجاور به مقابل یک زاویه مانند را در نظر میگیریم و آن را کتانژانت (Cot) مینامیم. با توجه به تعریفی که در بخش قبل برای تانژانت گفتیم میتوانیم رابطههای زیر را برای تانژانت یک زاویه بنویسیم.
و در نتیجه تانژانت را از تقسیم کسینوس بر سینوس یک زاویه بدست خواهیم آورد.
به تصویر زیر توجه کنید، نسبتهای مثلثاتی «تانژانت» (Tangent) و «کتانژانت» (Cotangent) را در آن پیدا کنید. البته نسبتهای مثلثاتی کسینوس و سینوس نیز در آن دیده میشوند. به خوبی مشخص است که رنگ نارنجی روی محور افقی، مقدار کسینوس، رنگ سبز روی محور عمودی، سینوس، رنگ بنفش، مقدار تانژانت و رنگ آبی روشن نیز کتانژانت زاویه را مشخص کرده است. روابط مثلثاتی به این ترتیب در تصویر ۷ به خوبی قابل مشاهدهاند.
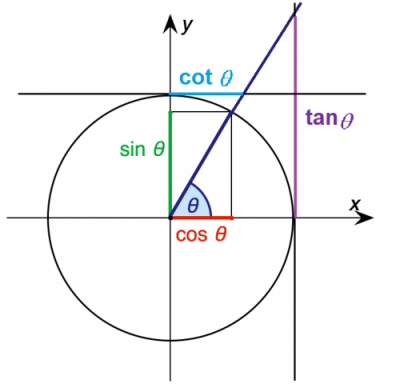
همانطور که در تصویر ۷ مشاهده میشود، تانژانت زاویه برابر با طول پاره خطی است که از محل برخورد خط زاویه بر محور کمکی (با رنگ بنفش) پدید میآید. این محور کمکی را موازی با محور عمودی ولی در محل برخورد دایره مثلثاتی با محول افقی ساختهایم. همچنین طول خطی که در محور کمکی دوم (با خط آبی) ساخته شده، کتانژانت را نشان میدهد. محور کمکی دوم براساس خطی موازی با محور افقی و از محل برخورد دایره مثلثاتی با محور عمودی کشیده میشود.
نکته: برای آنکه متوجه شوید چرا تانژانت یا کتانژانت زاویهای که در تعریف ارائه شد، با طول این خطوط برابر است باید از قضیه قضیه تالس کمک بگیرید. اثبات این موضوع در مطلب تانژانت و کتانژانت — نسبتهای مثلثاتی به زبان ساده آمده است.
رابطههای زیر را برای ارتباط بین مقدار سینوس و کسینوس یک زاویه با تانژانت و کتانژانت آن معرفی میکنیم. به خاطر سپاری این رابطهها در حل مسائل شما را یاری میرساند.
علامت نسبتهای مثلثاتی در جدول زیر نیز خلاصه شدهاند. مشخص است که هرجا سینوس و کسینوس هم علامت هستند، تابع تانژانت و کتانژانت، مثبت است و هرگاه یکی از آنها هم علامت با دیگری نباشد، مقدار تانژانت و کتانژانت، منفی خواهد بود.
جدول علامت نسبتهای مثلثاتی برای بخشهای مختلف دایره مثلثاتی
| نسبتهای مثلثاتی | ربع اول | ربع دوم | ربع سوم | ربع چهارم |
|---|---|---|---|---|
حال زمان مناسبی است که اندازه این نسبتهای مثلثاتی را برای زاویههای مختلف در جدول سینوس کسینوس تانژانت کتانژانت ارائه کنیم. از آنجایی که زاویههای معمول ۰، ۳۰، ۴۵، ۶۰ و ۹۰ هستند، محاسبات روابط مثلثاتی را در این زاویهها مورد بررسی قرار دادهایم. در تصویر ۸ چنین جدول را مشاهده میکنید. در اولین سطر، زاویه برحسب درجه و در سطر دوم، زاویه را با واحد رادیان مشخص کردهایم.
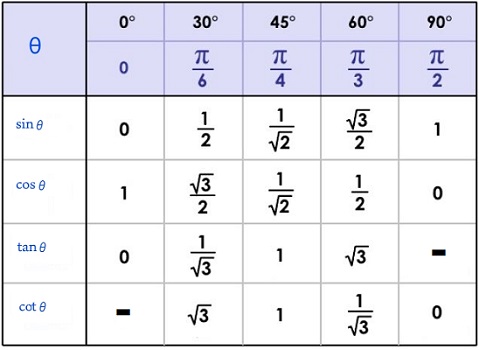
معکوس نسبت مثلثاتی
همانطور که دیدید، تانژانت و کتانژانت، معکوس یکدیگر هستند. معکوس سینوس و کسینوس را هم به عنوان یک تابع مثلثاتی میتوان در نظر گرفت. به معکوس کسینوس، «سِکانت» (SEC) و به معکوس سینوس، «کُسِکانت» (CSC) میگویند. پس رابطههای زیر برای تعریف آنها به کار میآید. البته باز هم از دایره مثلثاتی موجود در تصویر 4 کمک گرفتهایم.
بنابراین اگر بخواهیم مقادیر سکانت یا کسکانت زاویههای جدول مربوط به تصویر ۸ را محاسبه کنیم، کافی است که مقدارها را عکس کرده و برای سکانت یا کسکانت به کار بریم. برای مثال سکانت زاویه 60 درجه برابر با ۲ است. همچنین کسکانت زاویه ۴۵ درجه نیز ریشه دوم ۲ یا جذر ۲ خواهد بود.
رابطههای زیر بین تانژانت و کتانژانت با معکوس توابع مثلثاتی یعنی سکانت و کسکانت به صورت زیر است.
نسبت مثلثاتی زاویه بزرگتر از ۹۰ درجه
این بار به زاویههای بزرگتر از °۹۰ خواهیم پرداخت و نسبتهای مثلثاتی را برایشان مشخص خواهیم کرد. جدول زیر براساس زاویه حاده یا تند و میزان افزایش بر اساس یک دوران ۹۰ درجه () یا ۱۸۰ درجهای () حاصل شده است.
جدول نسبتهای مثلثاتی برای زاویههای بزرگتر از ۹۰ درجه
| دوران به اندازه یا ۹۰ درجه | دوران به اندازه یا ۱۸۰ درجه |
باز هم به کمک دایره مثلثاتی صحت این روابط را میتوان به سادگی و راحتی تحقیق کرد.
فرمولها و اتحادهای مثلثاتی
در ادامه به بعضی از فرمولها و روابط مثلثاتی اشاره خواهیم کرد که برای حل مسائل مثلثات به کار خواهند آمد.
نسبت مثلثاتی برای مجموع زاویهها
فرض کنید و دو زاویه باشند و بخواهیم نسبتها یا روابط مثلثاتی را برایشان محاسبه کنیم. دراین صورت اتحادهای زیر که به منظور بدست آوردن توابع مثلثاتی مجموع زاویهها است، مورد استفاده خواهند بود.
همین روابط مثلثاتی کمک میکنند که با دانستن یک زاویه، مقدار نسبت مثلثاتی سینوس و کسینوس را برای دو برابر این زاویه نیز محاسبه کنیم. به این ترتیب رابطههای زیر براساس معادلات بالا نوشته خواهند شد.
واضح است که کافی است در معادلات قسمت قبل، را با جایگزین کرده و نتایج را ساده کنید.
اگر به جای آن را با جایگزین کنیم، سینوکس و کسینوس تفاضل دو زاویه نیز بدست میآید.
زیرا میدانیم که و .
نکته: منظور از زاویه منفی، حرکت در جهت عقربههای ساعت روی دایره مثلثاتی است. به این ترتیب زاویه ۶۰- همان زاویه ۶۰ درجه است که در ناحیه ربع چهارم ساخته میشود. زاویه ۱۲۰- نیز در ربع سوم واقع است.
تابع سینوس به عنوان یک تابع مثلثاتی، فرد محسوب میشود زیرا با قرینه کردن زاویه، مقدار سینوس نیز قرینه میشود. ولی تابع کسینوس یک تابع زوج است. به این ترتیب میتوان به روابط زیر رسید.
همچنین با توجه به روابط بالا، میتوان تانژانت و کتانژانت را هم توابع فرد در نظر گرفت.
به همین ترتیب، سکانت نیز یک تابع زوج و کسکانت یک تابع فرد خواهد بود.
در زمینه استفاده از اتحادهای مثلثاتی به مثالهایی توجه کنید.
مثال
نشان دهید که رابطه زیر برقرار است.
راه حل: با توجه به رابطهای که بین سینوس و کسینوس برای بدست آوردن تانتژانت وجود دارد، عبارت سمت چپ بالا را گسترش میدهیم.
حال کسر بالا را در ضرب و تقسیم میکنیم. مشخص است که این عمل تغییری در رابطه بوجود نمیآورد و نتیجه نهایی یکسان خواهد بود. این کار یک راه حل عمومی برای حل کردن چنین رابطههایی است.
ولی برای ادامه کار، صورت کسر اول را بر مخرج کسر دوم تقسیم کرده و مخرج کسر اول را هم بر صورت کسر دوم تقسیم میکنیم. مشخص است که از رابطه طرفین وسطین استفاده شده. حال به رابطه زیر خواهیم رسید.
ابتدا طرف راست به شکل زیر ساده میکنیم.
پس از ساده کردن هر بخش، دوباره کسر حاصل را بر ضرب و تقسیم میکنیم.
به این ترتیب طرف راست رابطه بالا به صورت زیر نوشته خواهد شد. بنابراین اتحاد جدیدی برای جمع تانژانت دو زاویه ساخته میشود.
مثال
نشان دهید برای کتانژانت، مجموع دو زاویه از رابطه زیر تبعیت میکند.
راه حل
برای بدست آوردن پاسخ، همان مراحل قبلی را تکرار میکنیم ولی ابتدا، صورت و مخرج را به تقسیم خواهیم کرد. طرف چپ رابطه بالا را به صورت کسری و براساس تقسیم کسینوس بر سینوس مجموع دو زاویه مینویسیم.
حال صورت و مخرج کسر سمت راست را به تقسیم میکنیم. در نتیجه به رابطه زیر خواهیم رسید.
این بار دوباره کسر سمت راست را در ضرب و تقسیم میکنیم. در نتیجه رابطه نهایی حاصل میشود.
پس با ساده کردن رابطه اخیر به تساوی زیر خواهیم رسید.
اتحادهای زیر نیز برایتان کاربرد خواهد داشت.
تبدیل ضرب روابط مثلثاتی به جمع آنها
یکی از مثالهای ساده ولی با اهمیت در نسبت مثلثاتی سینوس و کسینوس، تبدیل ضرب این نسبتها به جمع است. در ادامه به معرفی آنها پرداختهایم.
برای مثال فرض کنید که میخواهیم تساوی اول را اثبات کنیم. ابتدا از سمت راست اقدام میکنیم و سینوس مجموع دو زاویه را برای هر دو قسمت، گسترش میدهیم.
پس از ساده سازی رابطه را به صورت زیر خواهیم داشت.
پس رابطه ابتدایی ثابت میشود.
تبدیل جمع روابط مثلثاتی به ضرب
این بار به سراغ اتحادهایی میرویم که بر اساس تبدیل جمع به ضرب عمل میکنند.
حل معادلات مثلثاتی
به یاد دارید که یک معادله، تساوی را نشان میدهد که در یک طرف آن مجهول قرار گرفته و هدف از حل معادله پیدا کردن مقدار این مجهول است. برای مثال ممکن است یک معادله مثلثاتی به صورت زیر نوشته شود.
مثال: اگر باشد، آنگاه سینوس این زاویه چقدر است؟
اگر رابطههای زیر را در نظر بگیریم، میتوانیم مقدار را مشخص کنیم.
در رابطه دوم مشخص است که مقدار کسینوس زاویه، دوبرابر سینوس همان زاویه است. کافی است این اطلاعات را در رابطه اول قرار داده و معادله را برای سینوس حل کنیم.
در نتیجه
پس میتوان نتیجه گرفت که مقدار سینوس چنین زاویهای برابر با است.
برای آشنایی بیشتر با روش حل معادلات مثلثاتی بهتر است مطلب معادلات مثلثاتی — به زبان ساده و نمونه سوال مثلثات — همراه با جواب از مجله فرادرس را بخوانید. در این نوشتارها، مثالهای متعدد به همراه روشهای متفاوت برای حل معادلات مثلثاتی معرفی و آموزش داده میشود.
به خاطر سپردن مقدار سینوس و کسینوس و همچنین تانژانت و کتانژانت که از روابط مثلثاتی هستند برای زاویههای مهم اهمیت ویژهای دارد. یک جدول تکمیل شده برای این روابط مثلثاتی در تصویر زیر آورده شده.
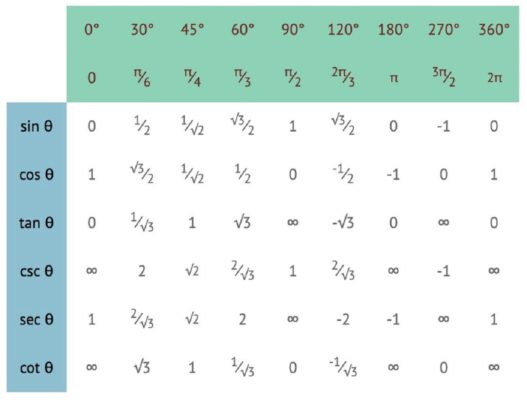
توابع و روابط مثلثاتی در شاخههای مختلف ریاضی
هرجایی که پای زاویه و شکلهای هندسی مانند مثلث به میان آید، مثلثات نیز پدیدار خواهد شد. نسبت یا روابط مثلثاتی کاربردهای مختلفی در علوم دیگر (غیر از ریاضی یا هندسه) دارند. این بخشها در ادامه معرفی شدهاند.
- مختصات قطبی
- مختصات استوانه ای
- مختصات کروی
- اعداد مختلط
- فضای برداری
- ضرب داخلی بردارها
- ضرب خارجی بردارها
- سری فوریه و تبدیل فوریه
- ...
روابط مثلثاتی در مختصات قطبی، کروی و استوانه ای
توابع یا نسبتهای مثلثاتی، برای تعیین محل یک نقطه در مختصات قطبی، کروی یا استوانهای به کار میرود. این مختصات برای بررسی شکلهای کروی یا حجمهای استوانهای بهتر قابل استفاده هستند به همین دلیل بسیاری از مسائل فیزیک یا مکانیک به کمک این گونه مختصات قابل حل است. در این دستگاههای مختصاتی، از طول بردار و زاویه بردار نسبت به مبدا مختصات استفاده میشود. در حالیکه در مختصات دکارتی از طول و عرض نقطه روی محورها برای تعیین محل نقطه کمک میگیریم. به این ترتیب در مختصات کروی، استوانهای یا قطبی، محل قرارگیری یک نقطه براساس که زاویه بردار است و طول بردار مشخص میشود.
روابط مثلثاتی در نمایش اعداد مختلط
همانطور که میدانید، یک عدد مختلط از دو بخش حقیقی و موهومی تشکیل شده. اگر بخش حقیقی را روی محور افقی و بخش موهومی را روی محور عمودی یک مختصات دکارتی در نظر بگیریم، آنگاه هر نقطه مثل در این فضا را به کمک مختصات قطبی به صورت زیر میتوان نشان داد.
واضح است که طول بردار و زاویه این بردار با محور افقی است. از طرفی میدانیم که همان بردار یکه موهومی است.
روابط مثلثاتی در فضای برداری
نمایش بردارها و همچنین دوران و یا ضرب داخلی و خارجی بردار، به کمک روابط مثلثاتی صورت میگیرد. بیشتر مباحث و مسائل مربوط به جبر خطی و فضاهای برداری به کمک فرمولهای مثلثات حل میشوند. بنابراین فراگیری مثلثات در این شاخه از ریاضی بسیار اهمیت دارد. از طرفی بردارها در فیزیک و مهندسی برای نمایش کمیتهای دارای جهت به کار میروند. پس اگر میخواهید در رشتههای مهندسی موفق باشید، حتما بر فرمول مثلثات باید تسلط خوبی داشته باشید.
در این بین قانون سینوسها و کسینوسها که به بررسی زاویههای یک مثلث به کمک اضلاع آن میپردازد، اهمیت زیادی دارند. برای آشنایی بیشتر با این دو قانون بهتر است مطالب، قانون سینوس ها (Law of Sines) — به زبان ساده و قانون کسینوس ها — به زبان ساده را مطالعه کنید. این زمینهها در در علوم دیگر به کار میروند
کاربرد مثلثات در علوم دیگر
بسیاری از مسائل مهندسی به کمک مثلثات قابل حل است. رشته برق، مکانیک، عمران و ... از مثلثات بیشترین بهره را میبرند. نقشه برداری در عمران، جهت و نحوه انتقال نیرو در مکانیک از مثلثات بهره برده و مسائل خود را به کمک این گونه توابع حل میکنند. همچنین در شیمی فضایی با استفاده از بردارها و زاویه بین آنها ساختار مولکولی و اتمی مواد را مشخص میکنند. در ادامه به بعضی از این علوم که روابط مثلثاتی در آن نقش مهمی ایفا میکند اشاره کردهایم.
ستاره شناسی
برای قرنها، از مثلثات کروی برای مکانیابی موقعیتهای خورشید، ماه و ستارهها استفاده شده است. پیش بینی خورشید گرفتگی و توصیف مدار سیارات بدون بهرهگیری از فرمول و روابط مثلثاتی امکانپذیر نبود. در دوران مدرن، از روش مثلثبندی در نجوم برای اندازهگیری فاصله تا ستارههای مجاور و همچنین در سیستمهای ناوبری ماهوارهای استفاده میشود.

جهت یابی
از نظر تاریخی، مثلثات برای تعیین موقعیت جغرافیایی (طول و عرض جغرافیایی) برای کشتیها و دریانوردی استفاده میشد. مثلثات هنوز هم در ناوبری از طریق ابزارهایی مانند سیستم موقعیتیاب جهانی (GPS) و هوش مصنوعی (AI) برای وسایل نقلیه خودران استفاده میشود.
نقشه برداری
در نقشه برداری زمین، مثلثات در محاسبه طول، مساحت و زاویههای نسبی بین اجسام استفاده میشود. در مقیاس بزرگتر، از مثلثات در جغرافیا برای اندازه گیری فواصل بین نشانهها و ترسیم نقشههای جغرافیایی بهره میبرند.
توابع متناوب و روابط مثلثاتی
توابع سینوس و کسینوس برای نظریه توابع متناوب نقشی اساسی دارند. امواج صوتی و نوری و همچنین حرکتهای دوار به کمک این روابط مثلثاتی توصیف میشوند. «ژوزف فوریه» (Joseph Fourier) کشف کرد که هر تابع پیوسته متناوب را میتوان بوسیله مجموع نامتناهی از توابع مثلثاتی توصیف کرد. حتی توابع نامتناوب را هم میتوان به عنوان انتگرال سینوسها و کسینوسها از طریق «تبدیل فوریه» (Fourier Transofrm) نشان داد. این کاربرد در زمینههای دیگر مانند مکانیک کوانتوم و ارتباطات به وفور دیده میشود.
نور و صوتی
مثلثات در بسیاری از علوم فیزیکی، از جمله آکوستیک و اپتیک، مورد استفاده قرار میگیرد در این حوزهها، از روابط مثلثاتی برای توصیف امواج صوت و نور و حل مسائل مربوط انتقال امواج استفاده میشوند.
کاربردهای دیگر روابط مثلثاتی
زمینه های دیگری که از مثلثات یا توابع مثلثاتی استفاده میکنند عبارتند از تئوری موسیقی، هندسه، تولید صوت، معماری، الکترونیک، زیست شناسی، تصویربرداری پزشکی (سی تی اسکن و سونوگرافی)، شیمی، نظریه اعداد و رمزنگاری، لرزه شناسی، هواشناسی، اقیانوس شناسی، فشرده سازی تصویر، آوایی، اقتصاد، مهندسی برق، مهندسی مکانیک، مهندسی عمران، گرافیک رایانهای، نقشه برداری، کریستالوگرافی و تولید بازیهای رایانهای.
آزمون روابط مثلثاتی
در این قسمت به منظور درک بهتر روابط مثلثاتی، تعدادی پرسش چهار گزینهای به صورت آزمون تهیه شده است.
تمرین و آزمون
حاصل برابر است با:
برای بهدست آوردن حاصل ، هر یک از عبارتها را به صورت جداگانه بهدست میآوریم. سپس، پاسخهای بهدست آمده را در یکدیگر ضرب میکنیم. در عبارت مثلثاتی از زاویه استفاده شده است. را میتوانیم به صورت زیر بنویسیم:
بنابراین برای یافتن روی دایره مثلثاتی باید از نقطه به اندازه در جهت عقربههای ساعت و به سمت بالا حرکت کنیم. این بدان معنا است که خط تصویر آینهای خط نسبت به محور عمودی است و در ناحیه دوم مثلثاتی قرار دارد. مختصات برابر مختصات است با این تفاوت که مختصات آن منفی خواهد بود.
به طور مشابه، را نیز میتوانیم به صورت زیر بنویسیم:
بنابراین برای یافتن روی دایره مثلثاتی باید از نقطه به اندازه در خلاف جهت عقربههای ساعت و به سمت پایین حرکت کنیم. این بدان معنا است که خط تصویر آینهای خط نسبت به محور افقی است و در ناحیه سوم مثلثاتی قرار دارد. مختصات برابر مختصات است با این تفاوت که مختصات و آن منفی خواهند بود. دو زاویه و در تصویر زیر و روی دایره مثلثاتی نشان داده شدهاند.
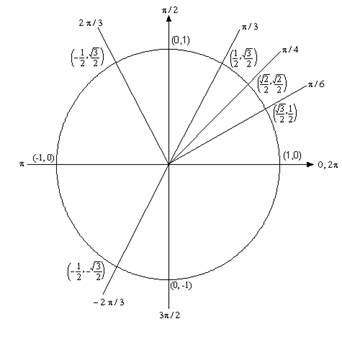
با استفاده از تصویر فوق داریم:
پاسخ معادله برابر است با:
برای حل معادلات مثلثاتی، ابتدا تابع مثلثاتی را در یک طرف تساوی نگه میداریم و اعداد را به طرف دیگر تساوی میبریم:
به دنبال تمام مقدارهای t میگردیم که به ازای آنها مقدار کسینوس برابر باشد. به دایره مثلثاتی نشان داده شده در تصویر زیر توجه کنید. با دقت به این دایره، به سرعت نتیجه میگیریم که حل معادله مثلثاتی فوق است. اما، همانطور که در تصویر فوق نشان داده شده است، زاویهای دیگری نیز به عنوان پاسخ معادله وجود دارد. برای یافتن این زاویه، نیاز به کمی هندسه داریم.
نخستین زاویه در ربع اول دایره مثلثاتی با جهت مثبت محور ها زاویه میسازد. همچنین، زاویه در ربع چهارم دایره مثلثاتی نیز میتواند پاسخ معادله مثلثاتی داده شده باشد. اما بیشتر ترجیهح میدهیم زوایای مثبت را به عنوان پاسخهای معادلات مثلثاتی در نظر بگیریم. برای داشتن زاویه مثبت، تنها باید به این نکته توجه داشته باشیم که زاویه با جهت مثبت محور برابر است.
راحتترین راه برای گرفتن زاویه مثبت دوم به این صورت است که یک دور کامل از زاویه صفر تا در خلاف جهت عقربههای ساعت روی دایره مثلثاتی حرکت کنیم، سپس به اندازه به عقب برگردیم. بنابراین، پاسخهای معادله برابر هستند با:
کدام یک از گزینههای زیر پاسخ معادله مثلثاتی در بازه نیست؟
برای حل معادلات مثلثاتی، ابتدا تابع مثلثاتی را در یک طرف تساوی نگه میداریم و اعداد را به طرف دیگر تساوی میبریم:
به دنبال تمام مقدارهای میگردیم که به ازای آنها مقدار سینوس برابر باشد. به دایره مثلثاتی نشان داده شده در تصویر زیر توجه کنید. هیچ زاویهای در ربع اول دایره مثلثاتی وجود ندارد که به ازای آن مقدار سینوس برابر شود. اما دو زاویه در ربع سوم و چهارم دایره مثلثاتی وجود دارند که به ازای آنها مقدار سینوس برابر میشود.
با توجه به آنکه ، زاویه در ربع سوم دایره مثلثاتی برابر زیر محور افقی خواهد بود.
به طور مشابه، زاویه موردنظر در ربع چهارم دایره مثلثاتی برابر یا است. اینجا به نقطه حساسی میرسیم. شاید با خود فکر کنید، پاسخ معادله فوق برابر است با:
اما پاسخ معادله متفاوت است، زیرا ما داریم، نه . بنابراین، داریم:
با تقسیم طرفین تساوی فوق بر ۵، مقدار برابر است با:
به ازای داریم:
اکنون باید پاسخهای قابلقبول در بازه را بهدست آوریم:
همچنین، پاسخ معادله به ازای مفادیر منفی n برابر است با:
بنابراین، جوابهای معادله مثلثاتی داده شده عبارت هستند از:
پاسخ معادله برابر است با:
صفر
معادله داده شده پاسخی ندارد.
قبل از حل این معادله به این نکته توجه داشته باشید که کمینه و بیشینه مقدار توابع سینوس و کسینوس، به ترتیب برابر ۱- و ۱+ است. از اینرو، معادله مثلثاتی داده شده پاسخی ندارد.
اگر باشد، حاصل برابر است با:
۳
۶
۲
۳-
اگر باشد، حاصل عبارت برابر است با:
مقدار در معادله کدارم است؟ (زاویه بین صفر و ۹۰ درجه است.)
عبارت برابر است با:
اگر باشد، حاصل برابر است با:
هیچکدام
اگر باشد، حاصل عبارت برابر است با:
۳+
۳-
گزینه یک و ۲
هیچکدام
خلاصه و جمعبندی
در این نوشتار با چند مفهوم از روابط مثلثاتی آشنا شده و همچنین نحوه به کارگیری دایره مثلثاتی را فرا گرفتید. همانطور که خواندید، مثلثات دریچهای به روی هندسه و همچنین مهندسی است. در بحثهای مربوط به مهندسی مکانیک، مهندسی عمران و ... مثلثات و روابط مثلثاتی نقش مهمی دارند. جدولهایی نیز برای بدست آوردن مقدار نسبتها یا روابط مثلثاتی مانند سینوس، کسینوس، تانژانت و کتانژانت برای زاویههای مختلف وجود دارد که این موضوع نیز در متن مورد اشاره قرار گرفت. ابزارهای نرمافزاری مختلفی نیز برای محاسبه این نسبتها وجود دارد که میتوان به کاربردیترین آنها یعنی اکسل پرداخت. محاسبات مربوط به روابط و نسبتها یا روابط مثلثاتی در متنی با عنوان توابع مثلثاتی در اکسل — از صفر تا صد در مجله فرادرس منتشر شده است.













اویلر ریاضیدان زاده ی کشور سوئیس می باشد نه آلمان
با سلام خدمت شما همراه گرامی؛
نکته بیان شده در متن اصلاح شد.
از بازخورد و همراهی شما با مجله فرادرس سپاسگزاریم.
عالی بود ممنونم از شما❤
ممنون ولی اون ناصرالدین طوسی رو اشتباه نوشتید. خواجه نصیرالدین طوسی درسته.
سلام
لطفا در قسمت (تبدیل ضرب روابط مثلثاتی به جمع آن ها) در اثبات اولی
پرانتز اول باید بنویسید :
(sinAcosB+sinBcosA)
با سلام و وقت بخیر؛
ممنون از دقت نظر شما. فرمول اصلاح شد.
از همراهی شما با مجله فرادرس سپاسگزاریم.
با سلام،
متن اصلاح شد. ممنون از دقت شما.
از همراهیتان با مجله فرادرس سپاسگزاریم.
با سلام
روابط Sec و Csc رو اشتباه نوشتین!
سلام رابطه ی تانژانت رو برعکس نوشتین
tan=y/x
همچنین علامت سکانت اشتباهه
sec(-X)=sec(X)
با سلام و وقت بخیر؛
هر دو فرمول اصلاح شدند. ممنون از دقت نظر شما.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام.
متن بازبینی و اصلاح شد.
سپاس از همراهی و بازخوردتان.