نمونه سوال مثلثات — همراه با جواب (+ دانلود فیلم آموزش رایگان)

در این آموزش‌های ریاضی مجله فرادرس، با مباحث مرتبط با مثلثات به طور کامل آشنا شدیم. در این آموزش، نمونه سوال مثلثات را ارائه کرده و جواب آن‌ها را نیز بیان خواهیم کرد. برای آشنایی با مفاهیم مثلثات و آمادگی برای حل نمونه سوال های این مبحث، پیشنهاد می‌کنیم آموزش‌های زیر را مطالعه کنید:

• سینوس، کسینوس و تانژانت یک زاویه — به زبان ساده
• تانژانت و کتانژانت — نسبت‌های مثلثاتی به زبان ساده
• دایره مثلثاتی — به زبان ساده
• توابع معکوس مثلثاتی — به زبان ساده
• آموزش اتحادهای مثلثاتی با فرمول اویلر — به زبان ساده

در ادامه، مثال‌هایی را بیان خواهیم کرد.

مثال ۱

اگر زاویه $$ \alpha $$ در ربع چهارم بوده و $$ \cos \alpha = \frac {1 } { 3 } $$، آن‌گاه مقدار $$ \sin \alpha $$ را محاسبه کنید.

حل: مقدار $$ \sin \alpha $$ را می‌توانیم از معادله $$ \sin ^ 2 \alpha + \cos ^ 2 \alpha = 1 $$ به دست آوریم:

$$ \large \begin {aligned} \sin ^ { 2 } \alpha + \cos ^ { 2 } \alpha & = 1 \\ \sin ^ { 2 } \alpha & = 1 - \cos ^ { 2 } \alpha \\ \sin \alpha & = \pm \sqrt { 1 - \cos ^ { 2 } \alpha } = \pm \sqrt { 1 - \left ( \frac { 1 } { 3 } \right ) ^ { 2 } } \\ & =\pm \sqrt { 1 - \frac { 1 } { 9 } } = \pm \sqrt { \frac { 8 } { 9 } } = \pm \frac { \sqrt { 8 } } { 3 } \end {aligned} $$

از آنجایی که زاویه $$ \alpha $$ در ربع چهارم قرار دارد، $$ \sin \alpha $$ منفی است. بنابراین، داریم: $$ \sin \alpha = - \frac {\sqrt{8}}{3} $$.

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

مثال 2

فرض کنید $$ x $$ در ربع سوم قرار دارد و $$ \sin x = - \frac { 2 } { 5 } $$. مقادیر زیر را به دست آورید.

(الف) $$ \cos x $$   (ب) $$ \sec x $$   (ج) $$ \tan x $$

حل الف: می‌توانیم مقدار $$ \cos x $$ را از رابطه $$ \sin ^ x + \cos ^ 2 x = 1 $$ محاسبه کنیم:

$$ \large \begin {aligned} \sin ^ { 2 } x + \cos ^ { 2 } x & = 1 \\ \cos ^ { 2 } x & = 1 - \sin ^ { 2 } x \\ \cos x & = \pm \sqrt { 1 - \sin ^ { 2 } x } = \pm \sqrt { 1 - \left ( - \frac { 2 }{ 5 } \right ) ^ { 2 } } \\ & = \pm \sqrt { 1 - \frac { 4 } { 2 5 } } = \pm \sqrt { \frac { 2 1 } { 2 5 } } = \pm \frac { \sqrt { 2 1 } } { 5 } \end {aligned} $$

از آنجایی که $$ x $$ در ربع سوم است، مقدار $$ \cos x $$ منفی است. بنابراین، $$ - \sqrt { \frac { 2 1 } { 2 5 }}  $$.

حل ب:

$$ \large \sec x = \frac { 1 } { \cos x } = \frac { 1 } { - \frac { \sqrt { 2 1 } } { 5 } } = - \frac { 5 } { \sqrt { 2 1 } } $$

حل ج:

$$ \large \tan x = \frac { \sin x } { \cos x } = \frac { - \frac { 2 }{ 5 } } { - \frac { \sqrt { 2 1 } } { 5 } } = - \frac { 2 } { 5 } \left ( - \frac { 5 } { \sqrt { 2 1 } } \right ) = \frac { 2 } { \sqrt { 2 1 } } $$

مثال ۳

مقدار $$ \cos \alpha $$ را بیابید که در آن $$ \alpha $$ یک زاویه حاده (کمتر از ۹۰ درجه) است و در رابطه $$ \tan \alpha = \frac {1} { 2 } $$ صدق می‌کند.

فیلم آموزش ریاضی ۲ – پایه یازدهم علوم تجربی در فرادرس

کلیک کنید

حل: با دو روش می‌توانیم مقدار مورد نظر را محاسبه کنیم.

روش اول: از آنجایی که $$ \alpha $$ یک زاویه حاده است، همه توابع مثلثاتی متناظر با آن مثبت هستند. بنابراین، با توجه به رابطه $$ \tan \alpha = \frac {1} { 2} $$ می‌توانیم مثلث قائم‌الزاویه زیر را رسم کنیم.

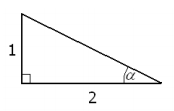
به سادگی و با استفاده از قضیه فیثاغورس می‌توانیم وتر مثلث بالا را به دست آوریم که اندازه آن برابر با $$ \sqrt {5} $$ خواهد بود. بنابراین، مقدار $$ \cos \alpha $$ برابر با $$ \frac {2} {\sqrt{5}} $$ به دست می‌آید.

روش دوم: از اتحاد معروف زیر استفاده می‌کنیم:‌

$$ \large \sin ^ { 2 } \alpha + \cos ^ { 2 } \alpha = 1 $$

با تقسیم رابطه بالا بر $$ \cos ^ 2 \alpha $$ داریم:

$$ \large \frac {\sin ^ { 2 } \alpha } { \cos ^ { 2 } \alpha } + \frac { \cos ^ { 2 } \alpha } { \cos ^ { 2 } \alpha } = \frac { 1 } { \cos ^ { 2 } \alpha } $$

$$ \large \tan ^ { 2 } \alpha + 1 = \frac { 1 } { \cos ^ { 2 } \alpha } $$

حال، دو طرف رابطه بالا را عکس می‌کنیم:

$$ \large \frac { 1 } { \tan ^ { 2 } \alpha + 1 } = \cos ^ { 2 } \alpha $$

با جذرگیری از دو طرف رابطه بالا، داریم:

$$ \large \pm \sqrt { \frac { 1 } { \tan ^ { 2 } \alpha + 1 } } = \cos \alpha $$

همان‌طور که می‌دانیم، زاویه $$ \alpha $$ حاده است و به همین دلیل $$ \cos \alpha $$ مثبت خواهد بود:

$$ \large \cos \alpha = \sqrt { \frac { 1 } { \tan ^ { 2 } \alpha + 1 } } = \sqrt { \frac { 1 } { \left ( \frac { 1 }{ 2 } \right ) ^ { 2 } + 1 } } = \sqrt { \frac { 1 } { \frac { 5 } { 4 } } } = \sqrt { \frac { 4 } { 5 } } = \frac { 2 } { \sqrt { 5 } } $$

مثال ۴

اگر $$ \cot A = 2 $$ باشد، مقدار $$ \sin A $$ را به دست آورید.

حل: از اتحاد معروف فیثاغورس استفاده می‌کنیم:

$$ \large \sin ^ { 2 } A + \cos ^ { 2 } A = 1 $$

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

با تقسیم رابطه بالا بر $$ \sin ^ 2 A $$، داریم:

$$ \large \frac { \sin ^ { 2 } A } { \sin ^ { 2 } A } + \frac { \cos ^ { 2 } A } { \sin ^ { 2 } A } = \frac { 1 } { \sin ^ { 2 } A } $$

$$ \large 1 + \cot ^ { 2 } A = \frac { 1 } { \sin ^ { 2 } A } $$

از آنجایی که $$ \cot A = 2 $$، می‌توان نوشت:

$$ \large \begin {aligned} 1 + 2 ^ { 2 } & = \frac { 1 } { \sin ^ { 2 } A } \\ 5 & = \frac { 1 } { \sin ^ { 2 } A } \\ \sin ^ { 2 } A & = \frac { 1 } { 5 } \\ \sin A & = \pm \frac { 1 } { \sqrt { 5 } } \end {aligned} $$

مثال ۵

عبارت زیر را ساده کنید:

$$ \large \frac {\tan t + \sin (-t) \cos (-t) } {\tan t } $$

حل:

$$ \large \begin {align*} & \frac { \tan t + \sin ( - t ) \cos ( - t ) } { \tan t } = \frac { \tan t - \sin t \cos t } { \tan t } = \frac { \frac { \sin t } { \cos t } - \sin t \cos t } { \frac { \sin t } { \cos t } } \\ & = \frac { \cos t } { \cos t } \cdot \frac { \frac { \sin t } { \cos t } - \sin t \cos t } { \frac { \sin t } { \cos t } } = \frac { \cos t \left ( \frac { \sin t } { \cos t } - \sin t \cos t \right ) } { \cos t \left ( \frac { \sin t } { \cos t } \right ) } \\ & = \frac { \sin t - \sin t \cos ^ { 2 } t } { \sin t } = \frac { \sin t \left ( 1 - \cos ^ { 2 } t \right ) } { \sin t } = \frac { \sin t \sin ^ { 2 } t } { \sin t } \\ & = \frac { \sin ^ { 3 } t } { \sin t } = \sin ^ { 2 } t \end {align*} $$

مثال ۶

اگر تساوی $$ 1+ \tan x = \frac {35} {12} \sin x $$ را داشته باشیم، مقدار $$ \sin 2x $$ را به دست آورید.

حل:

$$ \large \begin {aligned} 1 + \tan x & = \frac { 3 5 } { 12 } \sin x \\ 1 + \frac { \sin x } { \cos x } & = \frac { 3 5 } { 1 2 } \sin x \end {aligned} $$

با ضرب طرفین در $$ \cos x $$، داریم:

$$ \large \cos x + \sin x = \frac { 3 5 } { 1 2 } \sin x \cos x $$

حال دو طرف را به توان دو می‌رسانیم:‌

$$ \large ( \cos x + \sin x ) ^ { 2 } = \left ( \frac { 3 5 } { 1 2 } \sin x \cos x \right ) ^ { 2 } $$

$$ \large \cos ^ { 2 } x + \sin ^ { 2 } x + 2 \sin x \cos x = \left ( \frac { 3 5 } { 1 2 } \right ) ^ { 2 } \sin ^ { 2 } x \cos ^ { 2 } x $$

با در نظر گرفتن $$ a = \sin x \cos x $$، داریم:

$$ \large 1 + 2 a = \frac { 3 5 ^ { 2 } } { 1 2 5 a ^ { 2 } } $$

$$ \large 0 = 1 2 2 5 a ^ { 2 } - 2 8 8 a - 1 4 4 $$

جواب این معادله درجه دوم به صورت زیر خواهد بود:

$$ \large \begin {aligned} a _ { 1 , 2 } & = \frac { 2 8 8 \pm \sqrt { ( - 28 8 ) ^ { 2 } - 4 ( 1 2 2 5 ) ( - 1 4 4 ) } } { 2 \cdot 1 2 2 5 } = \frac { 2 8 8 \pm \sqrt { 8 2 9 4 4 + 7 0 5 6 0 0 } } { 2 4 5 0 } \\ & = \frac { 2 8 8 \pm \sqrt { 7 8 8 5 4 4 } } { 2 4 5 0 } = \frac { 2 8 8 \pm 8 8 8 } { 2 4 5 0 } = \left\{ \begin {array} {l} { \frac { 2 8 8 + 8 8 8 } { 2 4 5 0 } = \frac { 1 1 7 6 } { 2 4 5 0 } = \frac {1 2 } { 2 5 } } \\ { \frac {2 8 8 - 8 8 8 } { 2 4 5 0 } = \frac { - 6 0 0 } { 2 4 5 0 } = - \frac { 1 2 } { 4 9 } } \end {array} \right.\end {aligned} $$

با توجه به اینکه $$ a = \sin x \cos c$$، داریم:

$$ \large - \frac { 24 } { 49 }$$  یا  $$ \large \sin 2x = 2 \sin x \cos x = 2 a = \frac { 24 } { 25 }$$

مثال ۷

فرض کنید $$ \alpha + \beta + \gamma = 90 ^ \circ $$ که در آن، $$ \alpha$$، $$ \beta $$ و $$ \gamma$$ زاویه‌هایی حاده هستند. ثابت کنید: $$ \cot \alpha \cot \beta \cot \gamma = \cot \alpha + \cot \beta + \cot \gamma $$.

فیلم آموزش حسابان ۱ – پایه یازدهم – حل تمرین در فرادرس

کلیک کنید

حل: با استفاده از اطلاعات مسئله رابطه $$ \gamma = 90 ^ \circ - (\beta + \alpha) $$ و در نتیجه، $$ \cot \gamma = \cot ( 90 ^ \circ - (\beta + \alpha)) $$ را داریم. همچنین، اتحاد $$ \cot ( 90 ^ \circ - (\beta + \alpha)) = \tan (\beta + \alpha) $$ را می‌دانیم.

با در نظر گرفتن این موارد، می‌توان نوشت:

$$ \large \begin {aligned} & \cot \alpha + \cot \beta + \cot \gamma = \frac { 1 } { \tan \alpha } + \frac { 1 } { \tan \beta } + \tan ( \alpha + \beta ) = \frac { 1 } { \tan \alpha } + \frac { 1 } { \tan \beta } + \frac { \tan \alpha + \tan \beta } { 1 - \tan \alpha \tan \beta } \\ & = \frac { \tan \beta ( 1 - \tan \alpha \tan \beta ) } { \tan \alpha \tan \beta ( 1 - \tan \alpha \tan \beta ) } + \frac { \tan \alpha ( 1 - \tan \alpha \tan \beta ) } { \tan \alpha \tan \beta ( 1 - \tan \alpha \tan \beta ) } + \frac { \tan \alpha \tan \beta ( \tan \alpha + \tan \beta ) } { \tan \alpha \tan \beta ( 1 - \tan \alpha \tan \beta ) } \\ & = \frac { \tan \beta ( 1 - \tan \alpha \tan \beta ) + \tan \alpha ( 1 - \tan \alpha \tan \beta ) + \tan \alpha \tan \beta ( \tan \alpha + \tan \beta ) } { \tan \alpha \tan \beta ( 1 - \tan \alpha \tan \beta ) } \\ & = \frac { \tan \beta - \tan \alpha \tan ^ { 2 } \beta + \tan \alpha - \tan ^ { 2 } \alpha \tan \beta + \tan ^ { 2 } \alpha \tan \beta + \tan \alpha \tan ^ { 2 } \beta } { \tan \alpha \tan \beta ( 1 - \tan \alpha \tan \beta ) }
\\ & = \frac { \tan \beta + \tan \alpha } { \tan \alpha \tan \beta ( 1 - \tan \alpha \tan \beta ) } = \frac { 1 } { \tan \alpha } \cdot \frac { 1 } { \tan \beta } \cdot \frac { \tan \beta + \tan \alpha }{ ( 1 - \tan \alpha \tan \beta ) } = \frac { 1 } { \tan \alpha } \cdot \frac { 1 } { \tan \beta } \cdot \tan ( \alpha + \beta ) \\ & = \frac { 1 } { \tan \alpha } \cdot \frac { 1 } { \tan \beta } \cdot \cot \left ( 9 0 ^ { \circ } - ( \alpha + \beta ) \right ) = \frac { 1 } { \tan \alpha } \cdot \frac { 1 } { \tan \beta } \cdot \cot \gamma = \cot \alpha \cot \beta \cot \gamma
\end {aligned} $$

مثال ۸

تساوی‌های زیر را اثبات کنید:‌

(الف) $$ \large \frac { 2 } { \sin 2 x } = \tan x + \cot x $$

فیلم آموزش حسابان ۲ – پایه دوازدهم رشته ریاضی و فیزیک در فرادرس

کلیک کنید

حل:

$$ \large \begin {aligned} & \frac { 2 } { \sin 2 x } = \frac { 2 } { 2 \sin x \cos x } = \frac { 1 } { \sin x \cos x } = \frac { \sin ^ { 2 } x + \cos ^ { 2 } x } { \sin x \cos x } \\ & = \frac { \sin ^ { 2 } x } { \sin x \cos x } + \frac { \cos ^ { 2 } x } { \sin x \cos x } = \frac { \sin x } { \cos x } + \frac { \cos x } { \sin x } = \tan x + \cot x \end{aligned} $$

(ب) $$ \large \begin {aligned} \frac { \tan 2 x } { \tan x } = 1 + \frac { 1 } { \cos 2 x } \end {aligned} $$

حل:

$$ \large \begin {aligned} & \frac { \tan 2 x } { \tan x } = \frac { \frac { 2 \tan x } { 1 - \tan ^ { 2 } x } } { \tan x } = \frac { 2 \tan x } { 1 - \tan ^ { 2 } x } \cdot \frac { 1 } { \tan x } = \frac { 2 } { 1 - \tan ^ { 2 } x } = \frac { 2 } { 1 - \frac { \sin ^ { 2 } x } { \cos ^ { 2 } x } } = \frac { 2 } { \cos ^ { 2 } x } - \frac { \sin ^ { 2 } x } { \cos ^ { 2 } x } \\ & = \frac { 2 }{ \frac { \cos ^ { 2 } x - \sin ^ { 2 } x } { \cos ^ { 2 } x } } = 2 \cdot \frac { \cos ^ { 2 } x } { \cos ^ { 2 } x - \sin ^ { 2 } x } = \frac { 2 \cos ^ { 2 } x } { \cos ^ { 2 } x - \sin ^ { 2 } x } = \frac { \cos ^ { 2 } x + \cos ^ { 2 } x } { \cos ^ { 2 } x - \sin ^ { 2 } x } \\ &
= \frac { \cos ^ { 2 } x + \cos ^ { 2 } x + \sin ^ { 2 } x - \sin ^ { 2 } x } { \cos ^ { 2 } x - \sin ^ { 2 } x } = \frac { \cos ^ { 2 } x - \sin ^ { 2 } x } { \cos ^ { 2 } x - \sin ^ { 2 } x } + \frac { \cos ^ { 2 } x + \sin ^ { 2 } x } { \cos ^ { 2 } x - \sin ^ { 2 } x } \\ & = 1 + \frac { \cos ^ { 2 } x + \sin ^ { 2 } x } { \cos ^ { 2 } x - \sin ^ { 2 } x } = 1 + \frac { 1 } { \cos 2 x }
\end {aligned} $$

(ج) $$ \large \begin {aligned} \frac { \tan \left( \frac { \pi } { 4 } - x \right ) } { \tan \left ( \frac { \pi }{ 4 } + x \right ) } = \frac { 1 - \sin 2 x } { 1 + \sin 2 x } \end {aligned} $$

حل:

$$ \large \begin {aligned} & \frac { \tan \left( \frac { \pi } { 4 } - x \right ) } { \tan \left ( \frac { \pi }{ 4 } + x \right ) } = \frac { \frac { 1 - \tan x } { 1 + \tan x } } { \frac { \tan x + 1 } { 1 - \tan x } } \cdot \frac { 1 - \tan x } { 1 + \tan x } = \left ( \frac { 1 - \tan x } { 1 + \tan x } \right ) ^ { 2 } = \left ( \frac { 1 - \frac { \sin x } { \cos x } } { 1 + \frac { \sin x } { \cos x } } \right ) ^ { 2 } \\ & = \left ( \frac { \frac { \cos x } { \cos x } - \frac { \sin x } { \cos x } } { \frac { \cos x } { \cos x } + \frac { \sin x } { \cos x } } \right ) ^ { 2 } = \left ( \frac { \frac { \cos x } { \cos x } } { \frac { \cos x } { \cos x } } \right ) ^ { 2 } = \left ( \frac { \frac { \cos x - \sin x } { \cos x } } { \cos x } \cdot \frac { \cos x } { \cos x } \right ) ^ { 2 } \\ & = \left ( \frac { \cos x - \sin x } { \cos x + \sin x } \right ) ^ { 2 } = \frac { 1 - \sin 2 x } { 1 + \sin 2 x } \end{aligned} $$

(د) $$ \large \begin {aligned} \sin 35 ^ { \circ } + \sin 25 ^ { \circ } = \cos 5 ^ { \circ } \end {aligned} $$

حل:

$$ \large \begin {aligned} \sin 35 ^ { \circ } + \sin 25 ^ { \circ } & = \sin \left ( 3 0 ^ { \circ } + 5 ^ { \circ } \right ) + \sin \left ( 3 0 ^ { \circ } - 5 ^ { \circ } \right ) \\ & = \sin 30 ^ { \circ } \cos 5 ^ { \circ } + \cos 30 ^ { \circ } \sin 5 ^ { \circ } + \sin 30 ^ { \circ } \cos 5 ^ { \circ } - \cos 30 ^ { \circ } \sin 5 ^ { \circ } \\ & = 2 \sin 30 ^ { \circ } \cos 5 ^ { \circ } = 2 \left ( \frac { 1 } { 2 } \right ) \cos 5 ^ { \circ } = \cos 5 ^ { \circ } \end {aligned} $$

(ه) $$ \large \begin {aligned} \cos 1 2 ^ { \circ } - \cos 48 ^ { \circ } = \sin 18 ^ { \circ} \end {aligned} $$

حل:

$$ \large \begin {aligned} \cos 1 2 ^ { \circ } - \cos 48 ^ { \circ } & = \cos \left ( 3 0 ^ { \circ } - 1 8 ^ { \circ } \right ) - \cos \left ( 3 0 ^ { \circ } + 1 8 ^ { \circ } \right ) \\ & = \cos 3 0 ^ { \circ } \cos 1 8 ^ { \circ } + \sin 3 0 ^ { \circ } \sin 1 8 ^ { \circ } - \left ( \cos 3 0 ^ { \circ } \cos 1 8 ^ { \circ } - \sin 3 0 ^ { \circ } \sin 1 8 ^ { \circ } \right ) \\ & = \cos 3 0 ^ { \circ } \cos 1 8 ^ { \circ } + \sin 3 0 ^ { \circ } \sin 1 8 ^ { \circ } - \cos 3 0 ^ { \circ } \cos 1 8 ^ { \circ } + \sin 3 0 ^ {\circ} \sin 18^{\circ} \\ & = 2 \sin 3 0 ^ { \circ } \sin 18 ^ { \circ } = 2 \left ( \frac { 1 } { 2} \right ) \sin 18 ^ { \circ } = \sin 18 ^ { \circ} \end {aligned} $$

مثال ۹

مقدار عبارت $$ \frac { 1 + \tan 1 5 ^ { \circ } } { 1 - \tan 1 5 ^ { \circ } } $$ را محاسبه کنید.

حل: ابتدا $$ \tan 15^ \circ $$ را محاسبه می‌کنیم:

$$ \large \begin {aligned} \tan 15 ^ { \circ } & = \tan \left ( 4 5 ^ { \circ } - 3 0 ^ { \circ } \right ) = \frac { \tan 4 5 ^ { \circ } - \tan 3 0 ^ { \circ } } { 1 + \tan 4 5 ^ { \circ } \tan 30 ^ { \circ } } = \frac { 1 - \frac { 1 } { \sqrt { 3 } } } { 1 + \frac { 1 } { \sqrt { 3 } } } = \frac { 1 - \frac { 1 } { \sqrt { 3 } } }{ 1 + \frac { 1 } { \sqrt { 3 } } } \cdot \frac { \sqrt { 3 } }{ \sqrt { 3 } } \\ & = \frac { \sqrt { 3 } - 1 }{ \sqrt { 3 } + 1 } = \frac { \sqrt { 3 } - 1 } { \sqrt { 3 } + 1 } \cdot \frac { \sqrt { 3 } - 1 } { \sqrt { 3 } -1 } = \frac { 3 + 1 - 2 \sqrt { 3 } } { 2 } = \frac { 4 - 2 \sqrt { 2 } } { 2 } = \frac { 2 ( 2 -\sqrt { 3 } ) } { 2 } = 2 - \sqrt { 3 } \end {aligned} $$

حاصل عبارت مورد نظر نیز برابر است با:

$$ \large \frac { 1 + \tan 1 5 ^ { \circ } } { 1 - \tan 1 5 ^ { \circ } } = \frac { 1 + ( 2 - \sqrt { 3 } ) } { 1 - ( 2 - \sqrt { 3 } ) } = \frac { 3 - \sqrt { 3 } } { - 1 + \sqrt { 3 } } = \frac { \sqrt { 3 } ( \sqrt { 3 } - 1 ) } { \sqrt { 3 } - 1 } = \sqrt { 3 } $$

مثال ۱۰

اتحادهای زیر را در نظر بگیرید:

$$\large \sin ( x + y ) = \sin x \cos y + \cos x \sin y $$

$$ \large \cos (x + y ) = \cos x \cos y - \sin x \sin y $$

فرمولی برای $$ \tan ( x + y ) $$ بر حسب $$ \tan x $$ و $$ \tan y $$  به دست آورید.

فیلم آموزش ریاضی ۳ – پایه دوازدهم علوم تجربی در فرادرس

کلیک کنید

حل:

$$ \large  \tan ( x + y ) = \frac { \sin ( x + y ) } { \cos ( x + y ) } = \frac { \sin x \cos y + \cos x \sin y } { \cos x \cos y - \sin x \sin y } $$

اکنون صورت و مخرج را بر $$ \cos x \cos y $$ تقسیم کرده و عبارت مورد نظر را ساده می‌کنیم:

$$ \large \begin {aligned} \tan ( x + y ) & = \frac { \frac { \sin x \cos y + \cos x \sin y } { \cos x \cos y } } { \frac { \cos x \cos y - \sin x \sin y } { \cos x \cos y } } = \frac { \frac { \sin x \cos y } { \cos x \cos y } + \frac { \cos x \sin y } { \cos x \cos y } }{ \frac { \cos x \cos y } { \cos x \cos y } - \frac { \sin x \sin y }{ \cos x \cos y } } \\ & = \frac { \frac { \sin x } { \cos y } } { 1 -\frac { \sin x } { \cos x } \frac { \sin y } { \cos y } } = \frac { \tan x + \tan y } { 1 - \tan x \tan y } \end {aligned} $$

مثال ۱۱

در شکل زیر، مقدار $$ \alpha $$ را به دست آورید.

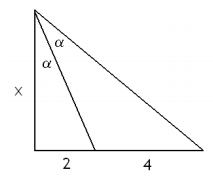
حل: با توجه به شکل بالا، روابط $$ \tan \alpha = \frac {2} { x } $$ و $$ \tan 2 \alpha = \frac {6} { x } $$ را می‌توان نوشت.

$$ \large \tan 2 \alpha = \frac {2 \tan \alpha } { 1- \tan ^ 2 \alpha } $$

$$ \large \begin {array} { l } { \frac { 6 } { x } = \frac { 2 \left ( \frac { 2 } { x } \right ) } { 1 - \left ( \frac { 2 } { x } \right ) ^ { 2 } } } \\ { \frac { 6 } { x } = \frac { \frac { 4 } { x } } { 1 - \frac { 4 } { x ^ { 2 } } } \cdot \frac { x ^ { 2 } }{ x ^ { 2 } } } \end {array} $$

$$ \large \begin {aligned} \frac { 3 } { x } & = \frac { 2 x }{ x ^ { 2 } - 4 } \\ 3 \left ( x ^ { 2 } - 4 \right ) & = 2 x ^ { 2 } \\ 3 x ^ { 2 } - 1 2 & = 2 x ^ { 2 } \\ x ^ { 2 } & = 1 2 \;\;\; \Rightarrow \;\;\; x = \pm \sqrt {12} \end {aligned} $$

مثال ۱۲

اتحادهای مثلثاتی زیر را اثبات کنید.

(۱) $$ \large \tan x \sin x + \cos x = \sec x $$

حل: از رابطه $$ \tan x = \frac {\sin x } { \cos x } $$ و اتحاد ساده $$ \sin ^ 2 x + \cos ^ 2 x = 1 $$ استفاده می‌کنیم. سمت چپ تساوی برابر است با:

$$ \large \begin {aligned} & \tan x \sin x + \cos x = \frac { \sin x } { \cos x } \cdot \sin x + \cos x = \frac { \sin ^ { 2 } x } { \cos x } + \cos x \\ & = \frac { \sin ^ { 2 } x } { \cos x } + \frac { \cos ^ { 2 } x } { \cos x } = \frac { \sin ^ { 2 } x + \cos ^ { 2 } x }{ \cos x } = \frac { 1 } { \cos x } = \sec x \end {aligned}
$$

فیلم آموزش ریاضی عمومی ۱ + حل مثال و تست کنکور کارشناسی ارشد در فرادرس

کلیک کنید

(۲) $$ \large \frac { 1 } { \tan x } + \tan x = \frac { 1 } { \sin x \cos x } $$

حل: از رابطه $$ \tan x = \frac {\sin x } { \cos x } $$ و اتحاد ساده $$ \sin ^ 2 x + \cos ^ 2 x = 1 $$ استفاده می‌کنیم. سمت چپ تساوی برابر است با:

$$ \large \frac { 1 } { \tan x } + \tan x = \frac { \cos x } { \sin x } + \frac { \sin x } { \cos x } = \frac { \cos ^ { 2 } x + \sin ^ { 2 } x } { \sin x \cos x } = \frac { 1 } { \sin x \cos x }
$$

(۳) $$ \large \sin x - \sin x \cos ^ { 2 } x = \sin ^ { 3 } x $$

حل: از $$ \sin x $$ فاکتور می‌گیریم و از اتحاد $$ \sin ^ 2 x + \cos ^ 2 x = 1 $$ استفاده می‌کنیم:

$$ \large \sin x - \sin x \cos ^ 2 x = \sin x ( 1 - \cos ^ 2 x ) = \sin x \cdot \sin ^ 2 x = \sin ^ 3 x $$

(۴) $$ \large \begin {aligned} \frac { \cos \alpha } { 1 + \sin \alpha } + \frac { 1 + \sin \alpha } { \cos \alpha } = 2 \sec \alpha \end {aligned} $$

حل:

$$ \large \begin {aligned} & \frac { \cos \alpha } { 1 + \sin \alpha } + \frac { 1 + \sin \alpha } { \cos \alpha } = \frac { \cos ^ { 2 } \alpha } { ( 1 + \sin \alpha ) \cos \alpha } + \frac { ( 1 + \sin \alpha ) ^ { 2 } } { ( 1 + \sin \alpha ) \cos \alpha } \\ & = \frac { \cos ^ { 2 } \alpha + ( 1 + \sin \alpha ) ^ { 2 } } { ( 1 + \sin \alpha ) \cos \alpha } = \frac { \cos ^ { 2 } \alpha + 1 + 2 \sin \alpha + \sin ^ { 2 } \alpha } { ( 1 + \sin \alpha ) \cos \alpha } \\ & = \frac { \cos ^ { 2 } \alpha + \sin ^ { 2 } \alpha + 1 + 2 \sin \alpha } { ( 1 + \sin \alpha ) \cos \alpha } = \frac { 2 + 2 \sin \alpha } { ( 1 + \sin \alpha ) \cos \alpha } \\ & = \frac { 2 ( 1 + \sin \alpha ) } { ( 1 + \sin \alpha ) \cos \alpha } = \frac { 2 } { \cos \alpha } = 2 \cdot \frac { 1 } { \cos \alpha } = 2 \sec \alpha \end {aligned}
$$

(۵) $$ \large  \begin {aligned} & \frac { \cos x } { 1 - \sin x } - \frac { \cos x } { 1 + \sin x } = 2 \tan x \end {aligned} $$

حل: از سمت چپ شروع کرده و مخرج مشترک می‌گیریم:

$$ \large \begin {aligned} & \frac { \cos x } { 1 - \sin x } - \frac { \cos x } { 1 + \sin x } = \frac { \cos x ( 1 + \sin x ) } { ( 1 - \sin x ) ( 1 + \sin x ) } - \frac { \cos x ( 1 - \sin x ) } { ( 1 - \sin x ) ( 1 + \sin x ) } \\ & = \frac { \cos x ( 1 + \sin x ) - \cos x ( 1 - \sin x ) } { ( 1 - \sin x ) ( 1 + \sin x ) } = \frac { \cos x + \cos x + \cos x \sin x - \cos x + \cos x \sin x }{ 1 - \sin ^ { 2 } x } \\ & = \frac { 2 \sin x \cos x } { \cos ^ { 2 } x } = \frac { 2 \sin x } { \cos x } = 2 \tan x \end {aligned} $$

(۶)‌ $$ \large \cos ^ 2 x = \frac { \csc x \cos x } { \tan x + \cot x } $$

حل: از سمت راست تساوی بالا شروع می‌کنیم و به سمت چپ آن می‌رسیم. همه عبارت‌ها را بر حسب $$ \sin x $$ و $$ \cos x $$ می‌نویسیم و آن‌ها را ساده می‌کنیم:

$$ \large \begin {aligned} & \frac { \csc x \cos x } { \tan x + \cot x } = \frac { \frac { 1 } { \sin x } \cdot \cos x } { \frac { \sin x } { \cos x } + \frac { \cos x } { \sin x } } = \frac { \frac { 1 } { \sin x } \cdot \frac { \cos x } { 1 } } { \frac { \sin ^ { 2 } x } { \sin x \cos x } + \frac { \cos ^ { 2 } x } { \sin x \cos x } } = \frac { \frac { \cos x } { \sin x } } { \frac { \sin ^ { 2 } x + \cos ^ { 2 } x } { \sin x \cos x } } \\ & = \frac { \frac { \cos x }{ \sin x } } { \frac { 1 } { \sin x \cos x } } = \frac { \cos x } { \sin x } \cdot \frac { \cos x \sin x } { 1 } = \frac { \cos ^ { 2 } x } { 1 } = \cos ^ { 2 } x \end{aligned}
$$

(۷) $$ \large \begin {aligned} \frac { \sin ^ { 4 } x - \cos ^ { 4 } x } { \sin ^ { 2 } x - \cos ^ { 2 } x } = 1 \end{aligned} $$

حل: می‌توانیم در صورت از اتحاد مزدوج استفاده کنیم و ساده‌سازی را انجام دهیم:

$$ \large \begin {aligned} & \frac { \sin ^ { 4 } x - \cos ^ { 4 } x } { \sin ^ { 2 } x - \cos ^ { 2 } x } = \frac { \left ( \sin ^ { 2 } x \right ) ^ { 2 } - \left ( \cos ^ { 2 } x \right ) ^ { 2 } } { \sin ^ { 2 } x - \cos ^ { 2 } x } \\ & = \frac { \left ( \sin ^ { 2 } x + \cos ^ { 2 } x \right ) \left ( \sin ^ { 2 } x - \cos ^ { 2 } x \right ) } { \sin ^ { 2 } x - \cos ^ { 2 } x } \\ & = \sin ^ { 2 } x + \cos ^ { 2 } x = 1 \end{aligned} $$

(۸) $$ \large \begin {aligned} \frac { \tan ^ { 2 } x } { \tan ^ { 2 } x + 1 } = \sin ^ { 2 } x \end{aligned} $$

حل:

$$ \large \begin {aligned} & \frac { \tan ^ { 2 } x } { \tan ^ { 2 } x + 1 } = \frac { \left ( \frac { \sin x } { \cos x } \right ) ^ { 2 } } { \left ( \frac { \sin x } { \cos x } \right ) ^ { 2 } + 1 } = \frac { \sin ^ { 2 } x } { \cos ^ { 2 } x } = \frac { \sin ^ { 2 } x } { \cos ^ { 2 } x } + \frac { \cos ^ { 2 } x } { \cos ^ { 2 } x } \\ & = \frac { \frac { \sin ^ { 2 } x } { \cos ^ { 2 } x } } { \frac { \sin ^ { 2 } x + \cos ^ { 2 } x } { \cos ^ { 2 } x } } = \frac { \frac { \sin ^ { 2 } x } { \cos ^ { 2 } x } }{ \frac { 1 } { \cos ^ { 2 } x } } = \frac { \sin ^ { 2 } x } { \cos ^ { 2 } x } \cdot \frac { \cos ^ { 2 } x } { 1 } = \sin ^ { 2 } x \end{aligned} $$

(۹) $$ \large \begin {aligned} \frac { 1 - \sin x } { \cos x } = \frac { \cos x } { 1 + \sin x } \end {aligned} $$

حل:

$$ \large \begin {aligned} & \frac { 1 - \sin x } { \cos x } = \frac { 1 -\sin x } { \cos x } \cdot 1 = \frac { 1 - \sin x } { \cos x } \cdot \frac { 1 + \sin x } { 1 + \sin x } = \frac { ( 1 - \sin x ) ( 1 + \sin x ) } { \cos x ( 1 + \sin x ) } \\ & = \frac { 1 - \sin ^ { 2 } x }{ \cos x ( 1 + \sin x ) } = \frac { \cos ^ { 2 } x } { \cos x ( 1 + \sin x ) } = \frac { \cos x } { 1 + \sin x } \end {aligned} $$

(۱۰) $$ \large \begin {aligned} 1 - 2 \cos ^ { 2 } x = \frac { \tan ^ { 2 } x - 1 } { \tan ^ { 2 } x + 1 } \end{aligned} $$

حل: از سمت راست تساوی به سمت چپ آن می‌رسیم:

$$ \large \begin {aligned} & \frac { \tan ^ { 2 } x - 1 } { \tan ^ { 2 } x + 1 } = \frac { \frac { \sin ^ { 2 } x } { \cos ^ { 2 } x } - 1 } { \frac { \sin ^ { 2 } x } { \cos ^ { 2 } x } + 1 } = \frac { \sin ^ { 2 } x } { \frac { \sin ^ { 2 } x } { \cos ^ { 2 } x } + \frac { \cos ^ { 2 } x } { \cos ^ { 2 } x } } = \frac { \sin ^ { 2 } x - \cos ^ { 2 } x } { \cos ^ { 2 } x } \\ & = \frac { \sin ^ { 2 } x - \cos ^ { 2 } x } { \cos ^ { 2 } x } \cdot \frac { \cos ^ { 2 } x } { \sin ^ { 2 } x + \cos ^ { 2 } x } = \frac { \sin ^ { 2 } x - \cos ^ { 2 } x } { \sin ^ { 2 } x + \cos ^ { 2 } x } \\ & = \frac { \sin ^ { 2 } x - \cos ^ { 2 } x } { 1 } = \sin ^ { 2 } x - \cos ^ { 2 } x \\ & = \left ( 1 - \cos ^ { 2 } x \right ) - \cos ^ { 2 } x = 1 - 2 \cos ^ { 2 } x \end{aligned} $$

(۱۱) $$ \large \begin {aligned} \tan ^ { 2 } \theta = \csc ^ { 2 } \theta \tan ^ { 2 } \theta - 1 \end {aligned} $$

حل: از سمت راست به سمت چپ می‌رسیم:

$$ \large \begin {aligned} & \csc ^ { 2 } \theta \tan ^ { 2 } \theta - 1 = \frac { 1 } { \sin ^ { 2 } \theta } \cdot \left ( \frac { \sin \theta } { \cos \theta } \right ) ^ { 2 } - 1 = \frac { 1 } { \sin ^ { 2 } \theta } \cdot \frac { \sin ^ { 2 } \theta } { \cos ^ { 2 } \theta } - 1 = \frac { 1 } { \cos ^ { 2 } \theta } - 1 \\ & = \frac { 1 } { \cos ^ { 2 } \theta } - \frac { \cos ^ { 2 } \theta } { \cos ^ { 2 } \theta } = \frac { 1 - \cos ^ { 2 } \theta } { \cos ^ { 2 } \theta } = \frac { \sin ^ { 2 } \theta } { \cos ^ { 2 } \theta } = \left ( \frac { \sin \theta } { \cos \theta } \right ) ^ { 2 } = \tan ^ { 2 } \theta \end {aligned} $$

(۱۲) $$ \large \begin {aligned} \sec x + \tan x = \frac { \cos x } { 1 - \sin x } \end{aligned} $$

حل: از سمت راست تساوی به سمت چپ آن می‌رسیم:

$$ \large \begin {aligned} & \frac { \cos x } { 1 - \sin x } = \frac { \cos x } { 1 - \sin x } \cdot 1 = \frac { \cos x } { 1 - \sin x } \cdot \frac { 1 + \sin x } { 1 + \sin x } = \frac { \cos x ( 1 + \sin x ) } { ( 1 - \sin x ) ( 1 + \sin x ) } \\ & = \frac { \cos x ( 1 + \sin x ) } { 1 - \sin ^ { 2 } x } = \frac { \cos x ( 1 + \sin x ) } { \cos ^ { 2 } x } = \frac { 1 + \sin x } { \cos x } = \frac { 1 } { \cos x } + \frac { \sin x } { \cos x }\\ & = \sec x + \tan x \end{aligned} $$

(۱۳) $$ \large \begin {aligned} & \frac { \csc \beta } { \sin \beta } -\frac { \cot \beta } { \tan \beta } = 1 \end{aligned} $$

حل: از سمت چپ تساوی شروع کرده و همه عبارات را بر حسب $$ \sin \beta $$ می‌نویسیم و آن‌ها را ساده می‌کنیم:

$$ \large \begin {aligned} & \frac { \csc \beta } { \sin \beta } -\frac { \cot \beta } { \tan \beta } = \frac { \frac { 1 } { \sin \beta } } { \frac { \sin \beta } { 1 } } - \frac { \frac { \cos \beta } { \sin \beta } } { \frac { \sin \beta } { \sin \beta } } = \frac { 1 } { \sin \beta } \cdot \frac { 1 } { \sin \beta } - \frac { \cos \beta } { \sin \beta } \cdot \frac { \cos \beta } { \sin \beta } \\ & = \frac { 1 } { \sin ^ { 2 } \beta } - \frac { \cos ^ { 2 } \beta } { \sin ^ { 2 } \beta } = \frac { 1 - \cos ^ { 2 } \beta } { \sin ^ { 2 } \beta } = \frac { \left ( \sin ^ { 2 } \beta + \cos ^ { 2 } \beta \right ) - \cos ^ { 2 } \beta } { \sin ^ { 2 } \beta } \\ & = \frac { \sin ^ { 2 } \beta } { \sin ^ { 2 } \beta } = 1 \end{aligned} $$

(۱۴) $$ \large \begin {aligned} & \sin ^ { 4 } x - \cos ^ { 4 } x = 1 - 2 \cos ^ { 2 } x \end{aligned} $$

حل:

$$ \large \begin {aligned} & \sin ^ { 4 } x - \cos ^ { 4 } x = \left ( \sin ^ { 2 } x \right ) ^ { 2 } - \left ( \cos ^ { 2 } x \right ) ^ { 2 } = \left ( \sin ^ { 2 } x + \cos ^ { 2 } x \right ) \left ( \sin ^ { 2 } x - \cos ^ { 2 } x \right ) \\ & = 1 \cdot \left ( \sin ^ { 2 } x - \cos ^ { 2 } x \right ) = \left ( 1 - \cos ^ { 2 } x \right ) -\cos ^ { 2 } x = 1 - 2 \cos ^ { 2 } x \end{aligned} $$

(۱۵) $$ \large \begin {aligned} ( \sin x - \cos x ) ^ { 2 } + ( \sin x + \cos x ) ^ { 2 } =2 \end{aligned} $$

حل:

$$ \large \begin {aligned} & ( \sin x - \cos x ) ^ { 2 } + ( \sin x + \cos x ) ^ { 2 } \\ & = \left ( \sin ^ { 2 } x + \cos ^ { 2 } x - 2 \sin x \cos x \right ) + \left ( \sin ^ { 2 } x + \cos ^ { 2 } x + 2 \sin x \cos x \right ) \\ & = 2 \sin ^ { 2 } x + 2 \cos ^ { 2 } x = 2 \left ( \sin ^ { 2 } x + \cos ^ { 2 } x \right ) = 2 \cdot 1 =2 \end{aligned} $$

(۱۶) $$ \large \begin {align*} \frac { \sin ^ { 2 } x + 4 \sin x + 3 } { \cos ^ { 2 } x } = \frac { \sin x + 3 } { 1 - \sin x } \end {align*} $$

حل:

$$ \large \begin {align*} & \frac { \sin ^ { 2 } x + 4 \sin x + 3 } { \cos ^ { 2 } x } = \frac { ( \sin x + 1 ) ( \sin x + 3 ) } { 1 - \sin ^ { 2 } x } \\ & = \frac { ( \sin x + 1 ) ( \sin x + 3 ) } { ( 1 + \sin x ) ( 1 - \sin x ) } = \frac { \sin x + 3 } { 1 - \sin x } \end {align*} $$

(۱۷) $$ \large \begin {aligned} \frac { \cos x } { 1 - \sin x } - \tan x = \sec x \end{aligned} $$

حل:

$$ \large \begin {aligned} & \frac { \cos x } { 1 - \sin x } - \tan x = \frac { \cos x } { 1 - \sin x } - \frac { \sin x } { \cos x } = \frac { \cos ^ { 2 } x - \sin x ( 1 - \sin x ) } { \cos x ( 1 - \sin x ) } \\ & = \frac { \cos ^ { 2 } x - \sin x + \sin ^ { 2 } x } { \cos x ( 1 - \sin x ) } = \frac { \left ( \cos ^ { 2 } x + \sin ^ { 2 } x \right ) - \sin x } { \cos x ( 1 - \sin x ) } = \frac { 1 - \sin x } { \cos x ( 1 - \sin x ) } = \frac { 1 } { \cos x } = \sec x \end{aligned} $$

(۱۸) $$ \large \begin {aligned} \tan ^ { 2 } x + 1 + \tan x \sec x = \frac { 1 + \sin x }{ \cos ^ { 2 } x } \end {aligned} $$

حل:

$$ \large \begin {aligned} & \tan ^ { 2 } x + 1 + \tan x \sec x = \frac { \sin ^ { 2 } x } { \cos ^ { 2 } x } + 1 + \frac { \sin x } { \cos x } \cdot \frac { 1 } { \cos x }\\ & = \frac { \sin ^ { 2 } x }{ \cos ^ { 2 } x } + \frac { \cos ^ { 2 } x } { \cos ^ { 2 } x } + \frac { \sin x } { \cos ^ { 2 } x } \\ & = \frac { \sin ^ { 2 } x + \cos ^ { 2 } x + \sin x } { \cos ^ { 2 } x } = \frac { 1 + \sin x }{ \cos ^ { 2 } x } \end {aligned} $$

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• انتگرال توابع مثلثاتی — از صفر تا صد
• نمونه سوال اتحاد و تجزیه — همراه با جواب
• مشتق توابع هذلولوی و معکوس آن‌ها — از صفر تا صد

^^

فیلم‌ های آموزش نمونه سوال مثلثات — همراه با جواب (+ دانلود فیلم آموزش رایگان)

فیلم آموزشی نمونه سوال مثلثات - محاسبه سینوس با توجه به کسینوس و بالعکس

فیلم آموزشی نمونه سوال مثلثات - محاسبه سینوس و کسینوس با توجه به تانژانت

فیلم آموزشی نمونه سوال مثلثات - ساده‌سازی عبارات مثلثاتی

فیلم آموزشی نمونه سوال مثلثات - محاسبه سینوس زاویه با داشتن تساوی مثلثاتی

فیلم آموزشی اثبات اتحاد‌های مثلثاتی با داشتن رابطه بین زوایا

فیلم آموزشی اثبات روابط مثلثاتی

فیلم آموزشی نمونه سوال مثلثات - محاسبات زوایای غیرمتعارف

فیلم آموزشی اثبات اتحادهای تانژانت مجموع زوایا

فیلم آموزشی حل مثال از ترکیب هندسه و مثلثات

فیلم آموزشی اثبات چند اتحاد مثلثاتی