سری فوریه (Fourier Series) – به زبان ساده

سری فوریه در ریاضیات، روشی برای بیان یک تابع به صورت مجموع چندین موج سینوسی است. در واقع با استفاده از این سری می‌توان یک تابع متناوب را به صورت حاصل جمع چندین تابع نوسانی بیان کرد. این توابع نوسانی، می‌توانند به فرم سینوسی، کسینوسی و یا به فرم مختلط آن‌ها بیان شوند. سری فوریه، تبدیل فوریه و انتگرال فوریه به طور گسترده در علوم گوناگون، برای تحلیل فیزیکی پارامترهای ریاضی، ساده‌سازی مسائل مختلف و حل آن‌ها مورد استفاده قرار می‌گیرد. این مطلب به بررسی مفهوم سری فوریه و شیوه محاسبه آن در توابع متنوع می‌پردازد. توجه داشته باشید که قبل از مطالعه‌ این مطلب، توصیه می‌شود مطلب توابع متعامد را مطالعه فرمایید.

مقدمه‌ای بر سری فوریه

مفهوم پایه در پیدایش سری‌های فوریه این است که توابع مختلف را می‌توان به کمک توابع سینوسی و کسینوسی بازنویسی کرد.

برای مثال، در شکل زیر دو موج مختلف با یکدیگر جمع شده‌اند و موج سوم را تولید کردند.

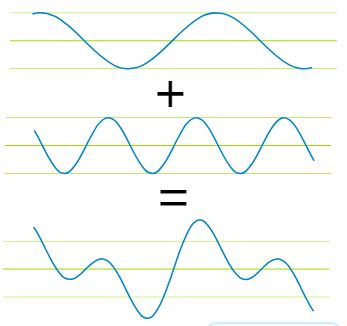
موج سینوسی اول، نشان دهنده تابع (sin(x و موج دوم تابع  (sin(2x را نمایش می‌دهد. در ادامه به بررسی یک مثال ملموس پرداخته می‌شود. در این مثال امکان بازنویسی یک تابع موج مربعی با استفاده از موج‌های سینوسی و کسینوسی مورد مطالعه قرار می‌گیرد.

موج مربعی

در این بخش، نمایش موج مربعی به کمک موج‌های سینوسی مورد مطالعه قرار می‌گیرد. بنابراین در ابتدا فرض کنید که موج مربعی به شکل زیر موجود است.

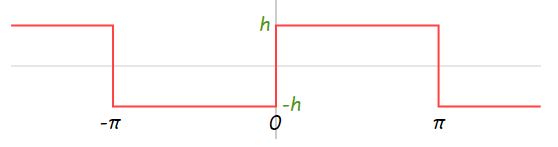
همانطور که مشاهده می‌شود این موج مربعی در مبدا مختصات ناپوستگی دارد و مقدار ماکزیمم آن در محدوده بازه صفر تا Π و Π- تا صفر رخ می‌دهد که مشابه با تابع سینوسی است. بنابراین برای نمایش این تابع به فرم مجموع چند تابع نوسانی، ابتدا تابع (sin(x را به شکل زیر نمایش می‌دهیم.

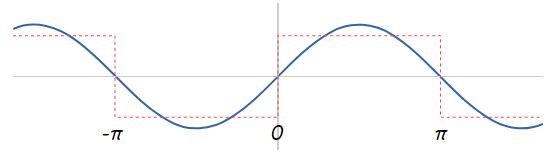
سپس برای تولید ناپیوستگی‌های موج مربعی نشان داده شده، تابع سینوسی 3/(sin(3x را نیز رسم می‌کنیم.

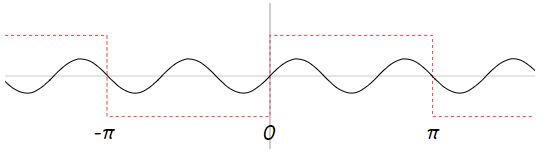
در ادامه، این دو تابع یعنی (sin(x و 3/(sin(3x را در بازه‌های نشان داده شده، با یکدیگر به فرم زیر جمع می‌کنیم.

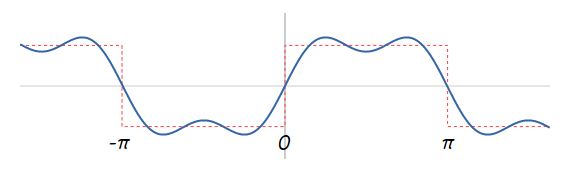
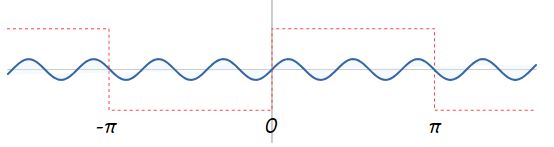
همانطور که مشاهده می‌شود، مجموع دو موج سینوسی نشان داده شده، تقریبا به فرم موج مربعی مطلوب ما در آمده است، بنابراین می‌توان نتیجه گرفت که روند مناسبی برای تولید این موج مربعی بر اساس توابع نوسانی انتخاب شده است. اما برای بهتر شدن نمایش آن، تابع 5/(sin(5x را نیز با آن‌ها جمع می‌کنیم. موج سینوسی 5/(sin(5x به شکل زیر قابل نمایش است.

حال مجموع دو موج سینوسی (sin(x و 3/(sin(3x در شکل 5 را با موج 5/(sin(5x در شکل 6 را محاسبه می‌کنیم. شکل زیر نتیجه نهایی جمع این سه تابع سینوسی را بیان می‌کند.

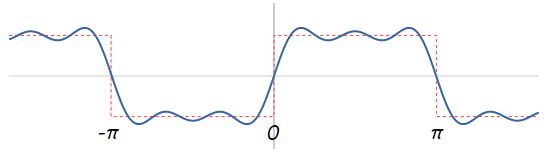
همانطور که بیان شد، موج نشان داده شده در شکل بالا، عبارت $$sin(x) + sin (3x)/3 + sin (5x)/5$$ را نمایش می‌دهد. با مقایسه موج مربعی و موج شکل بالا، می‌توان نتیجه گرفت که این موج نمایش نسبتا مناسبی از موج مربعی را به تصویر کشیده است. برای بهتر شدن نمایش این تابع، ۲۰ موج سینوسی را به فرم زیر با یکدیگر جمع می‌کنیم.

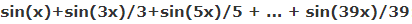
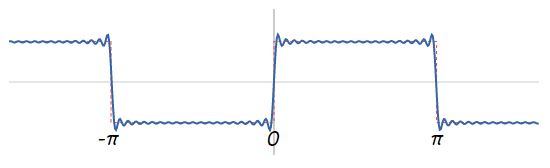
با مقایسه شکل ۷ و شکل ۸ می‌توان نتیجه گرفت که افزایش تعداد توابع سینوسی، فرم نهایی موج تولید شده را به موج مربعی نزدیکتر می‌کند. این روند را با در نظر گرفتن ۱۰۰ موج سینوسی به شکل زیر تکرار می‌کنیم.

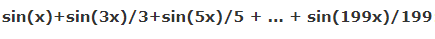
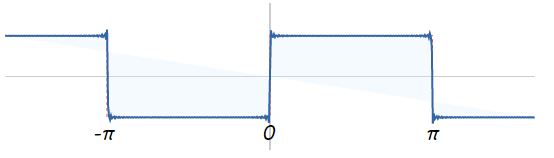
در صورتی که تعداد نامحدودی از توابع سینوسی را با الگوی بالا با یکدیگر جمع کنیم، یک موج مربعی تولید خواهد شد. این موضوع به شکل زیر نمایش داده می‌شود.

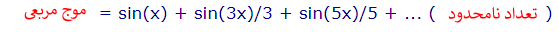
مراحلی که در بالا طی شد، ایده اصلی ایجاد سری فوریه را نشان می‌دهند. این مراحل برای تمام توابع نیز قابل انجام است. در واقع با استفاده از این روند می‌توان نشان داد که هر تابع را می‌توان به کمک تعداد نامحدودی از توابع سینوسی و یا کسینوسی تولید کرد.

ضرایب سری فوریه

در مثال قسمت قبل، برای تولید موج مربعی از توابع سینوسی به فرم $$sin((2k+1)x) / (2k+1)$$ استفاده شده است. در این قسمت به بررسی شیوه انتخاب این توابع و ضرایب آن‌ها پرداخته می‌شود. فرم کلی یک سری فوریه برای نمایش یک تابع به شکل زیر است.

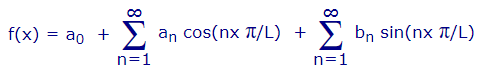
در این رابطه، (f(x، تابعی را نشان می‌دهد که قرار است به کمک توابع سینوسی بازنویسی شود. L، نصف دوره تناوب تابع را نمایش می‌دهد. a_n ،a₀ و b_n نیز ضرایب سری فوریه هستند که شیوه محاسبه آن‌ها در این قسمت مورد مطالعه قرار می‌گیرد.

توجه کنید که نماد سیگما ($$\sum$$) در عبارت دوم و سوم سمت راست معادله بالا، مجموع مقادیر عبارت مقابل سیگما را در n های مختلف ($$a_1 \cos(1x \pi / L)$$ ، $$a_2 \cos(2x \pi / L)$$ و ...) نمایش می‌دهد.

ضرایب a_n ،a₀ و b_n در رابطه سری فوریه (رابطه ۴) به شکل زیر محاسبه می‌شوند.

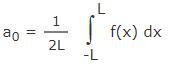
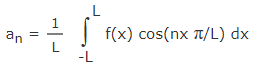
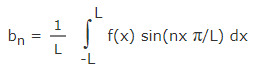
توجه کنید که عبارت انتگرالی رابطه 6، سطح خالص زیر نمودار تابع مقابل انتگرال (رابطه 8) را در محدوده بازه L- و L نمایش می‌دهد.

پاسخ نهایی عبارت انتگرالی را می‌توان با رسم تابع مورد نظر و اندازه‌گیری مساحت خالص زیر نمودار و یا محاسبه مستقیم انتگرال مربوطه، به دست آورد. روندی که برای محاسبه سری فوریه و ضرایب آن انجام می‌شود به شرح زیر است.

ابتدا تابع هدف را شناسایی و حاصل ضرب آن را در سینوس و یا کسینوس مشابه روابط بالا، به دست می‌آوریم. سپس انتگرال تابع حاصل را با محاسبه مستقیم و یا اندازه‌گیری مساحت خالص زیر نمودار محاسبه می‌کنیم. این کار را برای nهای مختلف انجام می‌دهیم، بنابراین ضرایب مختلف سری فوریه قابل محاسبه خواهند بود. در نهایت پس از محاسبه ضرایب سری فوریه، آن‌ها را در رابطه 4 قرار می‌دهیم.

توجه کنید که مراحل محاسبه ضرایب تبدیل فوریه، در نگاه اول اندکی زمان‌بر به نظر می‌رسد ولی بعد از آن که چند مسئله را از صفر تا صد حل کنید، محاسبه سری فوریه برای شما بسیار راحت خواهد بود.

مثال

در این قسمت، مثال ابتدای بحث برای موج مربعی تکرار می‌شود و شیوه محاسبه ضرایب سری فوریه آن‌ مورد ارزیابی قرار می‌گیرد. موج مربعی مورد نظر، در شکل زیر به تصویر کشیده شده است.

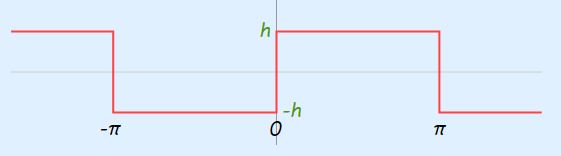
همانطور که مشاهده می‌کنید، دوره تناوب این موج برابر با 2Π است. بنابراین مقدار L در رابطه سری فوریه برابر با Π قرار داده می‌شود.

a₀ حاصل تقسیم مساحت سطح خالص تابع مربعی در بازه L- تا L+ بر دوره تناوب را نمایش می‌دهد. در واقع a₀ برابر با مقدار میانگین (f(x در محدوده L- تا L+ است. سطح خالص تابع مربعی در بازه مورد نظر در شکل زیر نشان داده شده است.

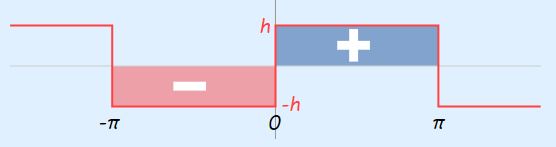
علامت مثبت در شکل بالا، سطح بالای محور مختصات را نشان می‌دهد که مساحت آن مثبت در نظر گرفته می‌شود و عبارت منفی سطح پایین محور مختصات را نشان می‌دهد و مساحت آن در مسائل مختلف برابر با مقداری منفی در نظر گرفته می‌شود.

با توجه به شکل بالا می‌توان نتیجه گرفت که سطح خالص در بازه مورد نظر برابر با صفر است. بنابراین همانطور که در رابطه زیر نشان داده شده، عبارت a₀ در سری فوریه، مقداری برابر با صفر دارد.

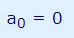
برای محاسبه ضریب a₁، مقدار n و L را در رابطه 6 به ترتیب برابر با ۱ و Π قرار می‌دهیم. بنابراین a₁ مطابق با رابطه زیر محاسبه می‌شود.

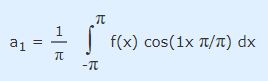
این عبارت (ضریب a₁) را می‌توان به شکل ساده شده زیر نمایش داد.

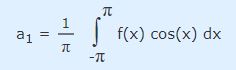
موج مربعی در نقطه x=0 ناپیوستگی دارد، بنابراین انتگرال فوق را در دو بازه Π- تا 0 و 0 تا Π+ محاسبه می‌کنیم. توجه کنید که مقدار تابع موج مربعی در بازه Π- تا 0 برابر با h- و مقدار آن در بازه 0 تا Π+ برابر با h+ است. در ادامه انتگرال فوق در بازه Π- تا 0 را به شکل زیر نمایش می‌دهیم.

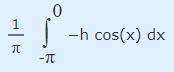
عبارت h- یک ثابت است که می‌توان آن را به خارج انتگرال منتقل کرد.

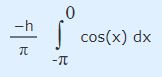
برای محاسبه انتگرال فوق به دو صورت می‌توان عمل کرد. روش اول رسم نمودار تابع (cos(x و محاسبه سطح زیر نمودار آن است و روش دوم محاسبه مستقیم انتگرال فوق است. در این مطلب، از روش اول استفاده می‌شود. بنابراین نمودار (cos(x را در بازه Π- تا 0 به شکل زیر نمایش می‌دهیم.

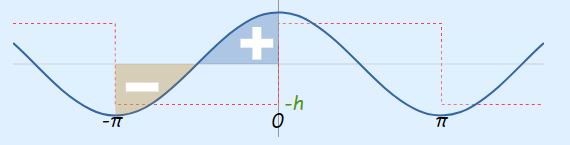
همانطور که مشاهده می‌شود، مقدار سطح خالص زیر نمودار بالا در بازه نشان داده شده، برابر با صفر است. بنابراین داریم:

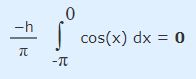
به صورت مشابه، سطح خالص زیر نمودار تابع (cos(x را در بازه 0 تا Π+ به شکل زیر بازنویسی می‌کنیم.

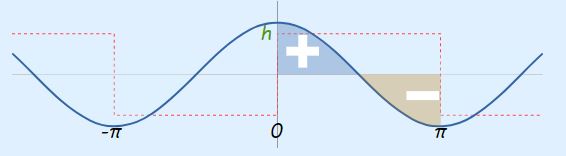
همانطور که مشاهده می‌شود مقدار سطح خالص زیر نمودار بالا در بازه 0 تا Π+ نیز برابر با صفر است. در نهایت می‌توان نتیجه گرفت که عبارت a₁ در سری فوریه برابر با صفر است و رابطه آن به شکل زیر بیان می‌شود.

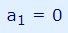
روند فوق را به شکل مشابه برای محاسبه ضریب a₂ نیز طی می‌کنیم. بنابراین ابتدا مساحت خالص زیر نمودار تابع (cos(2x را در بازه Π- تا 0 به شکل زیر نمایش می‌دهیم.

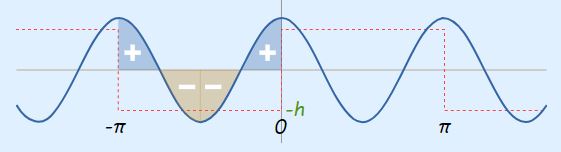
مشاهده می‌شود که اندازه سطح خالص زیر نمودار بالا در بازه نشان داده شده برابر با صفر است. حال به محاسبه مساحت سطح زیر نمودار تابع (cos(2x در بازه 0 تا Π+ می‌پردازیم.

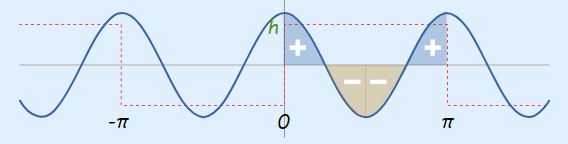
همانطور که مشاهده می‌شود، مساحت خالص زیر نمودار تابع (cos(2x در بازه 0 تا Π+ نیز برابر با صفر است. بنابراین می‌توان نتیجه گرفت که عبارت a₂ در سری فوریه مقداری برابر با صفر دارد و رابطه آن به شکل زیر نمایش داده می‌شود.

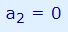
بر این اساس با توجه به تابع ()cos و روندی که در این مرحله نشان داده شد، می‌توان نتیجه گرفت که تمام ضرایب a برابر با مقدار صفر هستند.

در ادامه به محاسبه ضریب b در سری فوریه می‌پردازیم. در این قسمت، تابع هدف به فرم سینوسی است. در صورتی که در رابطه 7 مقدار n و L را به ترتیب برابر با ۱ و Π قرار دهیم، مقدار b₁ به فرم زیر محاسبه می‌شود.

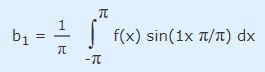
این رابطه را می‌توان به شکل ساده شده زیر نمایش داد.

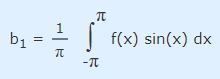
مشابه روندی که برای محاسبه ضریب a طی شد، به دلیل وجود ناپیوستگی در تابع موج مربعی در نقطه 0=x، محاسبات را به دو بازه Π- تا 0 و 0 تا Π+ تقسیم می‌کنیم. مقدار عبارت بالا در بازه Π- تا 0 به شکل زیر در می‌آید.

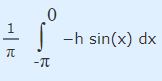
با توجه به اینکه، مقدار h در رابطه بالا ثابت است، می‌توان آن را به بیرون از انتگرال منتقل کرد.

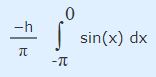
در ادامه برای محاسبه انتگرال بالا، عبارت جلوی انتگرال یعنی تابع (sin(x را در بازه Π- تا 0 به شکل زیر نمایش داده می‌شود.

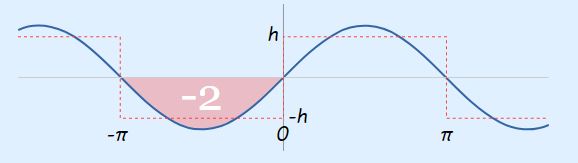
همانطور که در مبحث انتگرال اشاره شد، انتگرال (sin(x برابر با (cos(x- است. بنابراین می‌توان انتگرال موجود در رابطه بالا را در بازه مورد نظر به شکل زیر محاسبه کرد.

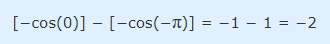
مقدار محاسبه شده در رابطه ۲۲، در ناحیه صورتی رنگ شکل ۱۶ به تصویر کشیده شده است. با استفاده از رابطه بالا، فرم نهایی انتگرال نشان داده شده در معادله ۲۱ به شکل زیر در می‌آید.

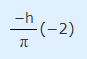
در ادامه به محاسبه انتگرال رابطه ۱۹ در بازه 0 تا Π+ پرداخته می‌شود. این انتگرال به فرم زیر قابل بازنویسی است.

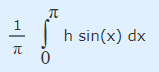
مشابه انتگرال قبل، با توجه به ثابت بودن پارامتر h، می‌توان آن را به بیرون از انتگرال منتقل کرد. این موضوع در رابطه زیر نشان داده شده است.

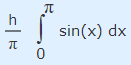
این انتگرال را نیز می‌توان مشابه با رابطه 22، به شکل زیر محاسبه کرد.

سطح زیر نمودار رابطه 25، در بازه 0 تا Π+ در شکل زیر نشان داده شده است.

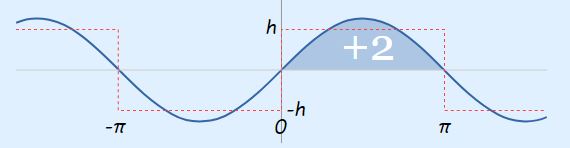
بنابراین برای محاسبه فرم نهایی ضریب b₁، مقدار این ضریب در دو بازه Π- تا 0 و 0 تا Π+ که در رابطه 19 نشان داده شد را با یکدیگر جمع می‌کنیم.

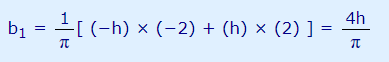
در ادامه، محاسبه ضریب b₂ مورد مطالعه قرار می‌گیرد. برای این منظور ابتدا به محاسبه انتگرال مربوط به این ضریب در بازه Π- تا 0 پرداخته می‌شود. این انتگرال به فرم زیر قابل بیان است.

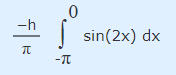
برای محاسبه این انتگرال، ابتدا تابع (sin(2x را رسم و در نهایت سطح زیر این نمودار در بازه Π- تا 0 محاسبه می‌کنیم. این تابع در شکل زیر به تصویر کشیده شده است.

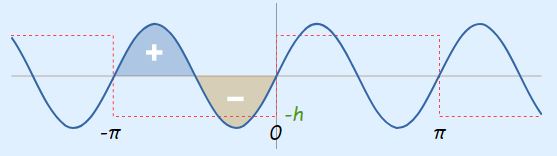
همانطور که مشاهده می‌شود، سطح خالص زیر نمودار بالا در بازه مورد نظر برابر با صفر است. بنابراین در محدوده Π- تا 0 مقدار انتگرال رابطه 28 برابر با صفر است. محاسبه این انتگرال در بازه 0 تا Π+ نیز نتیجه مشابهی را ارائه می‌دهد. بنابراین ضریب b₂ به فرم رابطه زیر در می‌آید.

این روند را برای محاسبه ضرایب b₃ و b₄ نیز ادامه می‌دهیم. انتگرال مربوط به ضریب b₃ در بازه Π- تا 0 به فرم رابطه زیر نمایش داده می‌شود.

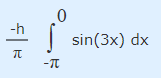
برای محاسبه این انتگرال، ابتدا عبارت مقابل انتگرال را مطابق شکل زیر در بازه مورد نظر رسم می‌کنیم و سپس سطح خالص زیر نمودار رسم شده را مورد ارزیابی قرار می‌دهیم.

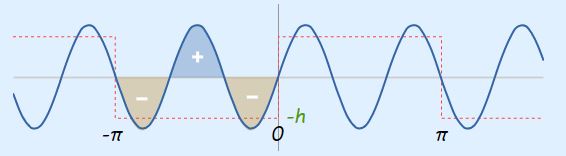
همانطور که مشاهده می‌شود دو سطح هم‌اندازه با علامت مخالف در شکل بالا یکدیگر را خنثی می‌کنند ولی سطح سوم با علامت منفی باقی می‌ماند. این مقدار باقی‌ مانده، برابر با یک سوم مقدار محاسبه شده در انتگرال b₁ در بازه مورد نظر است.

در ادامه به بررسی عبارت مقابل انتگرال ضریب b₃ در بازه 0 تا Π+ می‌پردازیم. بر این اساس، شکل تابع آن را در بازه مربوطه به شکل زیر نمایش می‌دهیم.

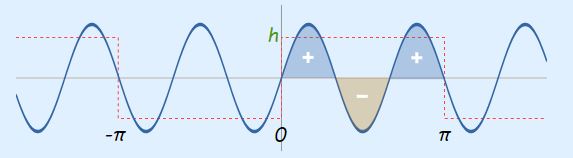
همانطور که مشاهده می‌شود دو سطح مثبت و منفی در رابطه بالا یکدیگر را خنثی می‌کنند ولی سطح سوم با علامت منفی باقی می‌ماند که مقدار آن برابر با یک سوم مقدار محاسبه شده در انتگرال b₁ در بازه مورد نظر است. بنابراین با استفاده از دو شکل بالا و توضیحات مربوطه می‌توان نتیجه گرفت که اندازه ضریب b₃ در سری فوریه یک سوم اندازه ضریب b₁ است و داریم:

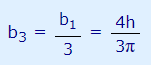
بر این اساس می‌توان نتیجه گرفت که در مسئله بیان شده، زمانی که n در رابطه ۷، یک عدد زوج باشد، فرم کلی عبارت مقابل انتگرال ضریب b به شکل زیر نمایش داده می‌شود.

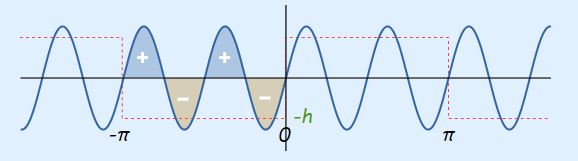
همانطور که مشاهده می‌شود، در این حالت، مساحت سطح زیر نمودار برابر با صفر است. بنابراین ضریب b برای nهای زوج مقداری برابر با صفر دارد. شکل عبارت مقابل انتگرال ضریب b، برای nهای فرد نیز به شکل زیر قابل نمایش است.

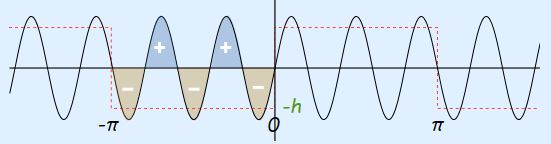
مطابق شکل بالا می‌توان نتیجه گرفت که، در این حالت، تمامی سطوح به غیر از یک سطح همدیگر را خنثی می‌کنند. این سطح باقی ‌مانده  $$1/n$$ سطح کلی را می‌پوشاند. بنابراین عبارت b_n در حالتی که n عددی فرد است مشابه با b₁ و b₃ به شکل کلی زیر بیان می‌شود.

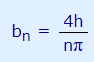
همانطور که اشاره شد ضریب b_n در حالتی که n عددی زوج باشد، برابر با صفر است. حال به منظور بیان فرم نهایی سری فوریه برای موج مربعی، مقادیر محاسبه شده را در رابطه کلی سری فوریه به شکل زیر جایگذاری می‌کنیم.

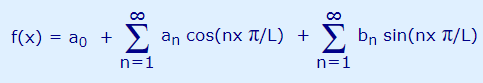
در این رابطه a0 و a_n برابر با صفر هستند و b_n نیز زمانی که n زوج باشد، مقداری برابر با صفر دارد. همچنین مقدار b_n زمانی که n فرد باشد برابر با $$4h/n \pi$$ است. بنابراین می‌توان نتیجه گرفت که فرم نهایی سری فوریه تابع مورد نظر به شکل زیر خواهد بود.

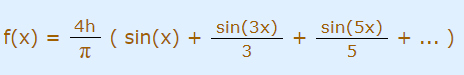
در مثال بالا نشان داده شد که برای محاسبه ضرایب سری فوریه یک تابع، از دو روند کلی مختلف می‌توان استفاده کرد. راه اول، رسم عبارت مقابل انتگرال و اندازه‌گیری مساحت خالص زیر نمودار آن است و در راه دوم می‌توان از روش‌های مختلف انتگرال‌گیری برای محاسبه ضرایب سری فوریه استفاده کرد. این روش‌ها در مطلب «انتگرال و روش های محاسبه — به زبان ساده» وبلاگ فرادرس توضیح داده شده‌اند.

همانطور که بیان شد، سری فوریه روشی است که از آن برای بیان یک تابع به صورت مجموع چندین موج سینوسی استفاده می‌شود. در واقع با استفاده از این سری می‌توان یک تابع متناوب را به صورت مجموع چندین تابع نوسانی بیان کرد. این توابع نوسانی، می‌توانند به فرم سینوسی، کسینوسی و یا به فرم مختلط آن‌ها بیان شوند. این مطلب به صورت جامع و عمیق، مفهوم سری فوریه و شیوه محاسبه آن در توابع مختلف را مورد بررسی قرار داده است.