توابع مثلثاتی در اکسل — از صفر تا صد
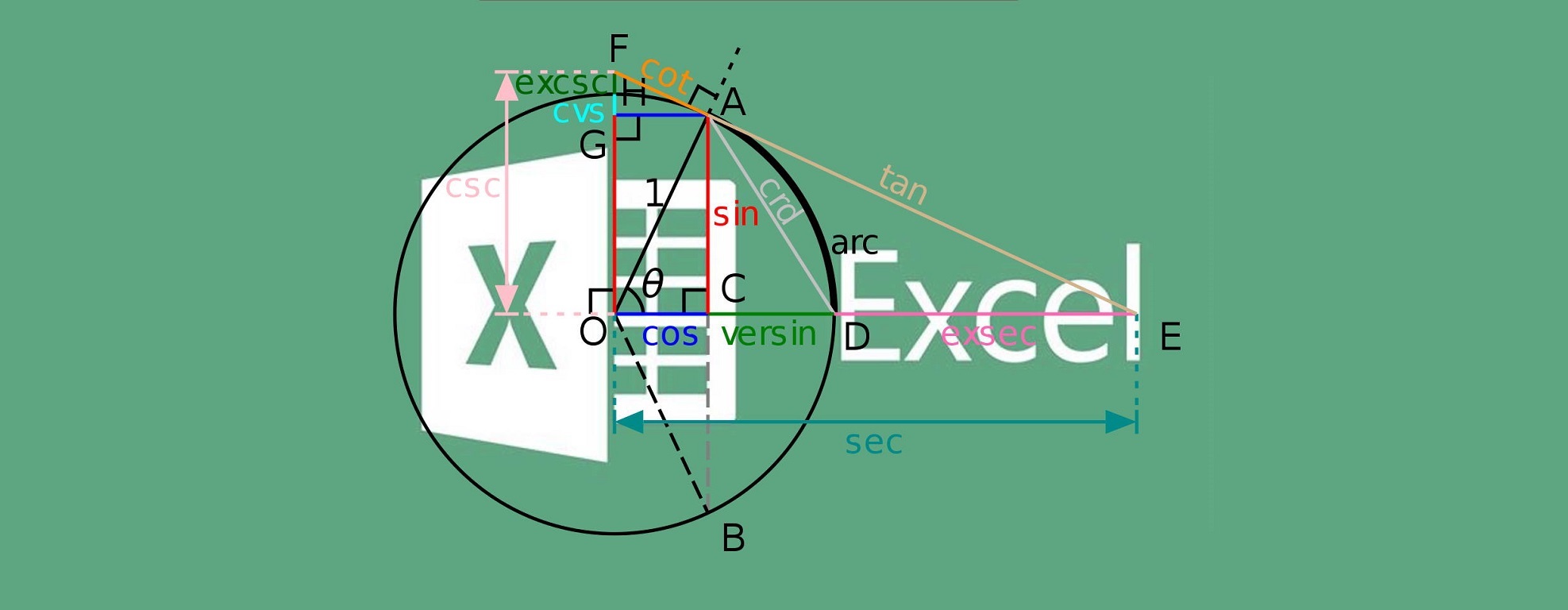
مثلثات (Trigonometry) یکی از شاخههای مهم در ریاضیات است که به روابط بین زاویهها و اضلاع در یک مثلث میپردازد. نسبتهای مثلثاتی مانند سینوس (Sin)، کسینوس (Cos)، تانژانت (Tan) و کتانژانت (Cot) از معروفترین توابعی هستند که در مثلثات، هندسه و علوم مهندسی بسیار کاربرد دارند. در این نوشتار توابع مثلثاتی در اکسل را مورد بررسی قرار میدهیم و با نحوه محاسبه آنها آشنا میشویم.
به منظور آشنایی بیشتر با نسبتهای مثلثاتی بهتر است ابتدا نوشتار دایره مثلثاتی — به زبان ساده و سینوس، کسینوس و تانژانت یک زاویه — به زبان ساده را مطالعه کنید. البته خواندن تانژانت و کتانژانت — نسبتهای مثلثاتی به زبان ساده نیز خالی از لطف نیست. همچنین نحوه فرمول نویسی در اکسل نیز در نوشتار فرمول نویسی در اکسل – آموزش مقدماتی آمده است. با خواندن آن، بسیاری از اصطلاحات مطرح شده در این مطلب را بهتر درک خواهید کرد و میتوانید به راحتی توابع مثلثاتی در اکسل را به کار ببرید.
توابع مثلثاتی در اکسل
به منظور آغاز بحث، ابتدا به معرفی مختصر بعضی از نسبتهای مثلثاتی در ریاضیات میپردازیم و سپس با شیوه محاسبه توابع مثلثاتی در اکسل آشنا خواهیم شد.
همانطور که میدانید، دایرهای که شعاع آن برابر با واحد است، دایره مثلثاتی نامیده میشود. البته ممکن است شعاع دایره مثلثاتی، یک متر، ۱۲ سانتیمتر و حتی ۱ کیلومتر باشد ولی نکته جالب آن است که در هر یک از این دایرهها، نسبتهای مثلثاتی مربوط به زاویههای ایجاد شده، بطور یکسان محاسبه میشوند و هر یک از این طولها را به عنوان واحد در نظر گرفته میشوند.
هر دایره مثلثاتی دارای یک مرکز با مختصات نقطه (0,0) است. نام محور افقی در این مختصات، محور «کسینوس» (Cos) و اسم محور عمودی نیز «سینوس» (Sin) است. در تصویر زیر یک نمونه از دایره مثلثاتی را میبینید. زاویه $$\theta$$ نیز در دایره مثلثاتی کاملا مشخص شده است.
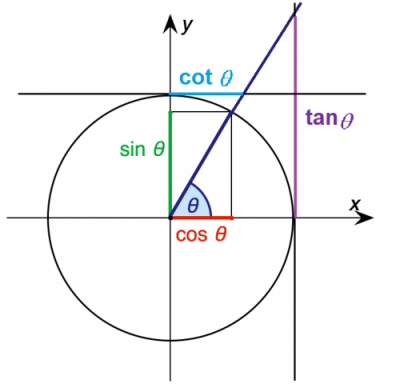
همانطور که دیده میشود، خطی که از محل برخورد دایره مثلثاتی با محور افقی جدا شده، محور تانژانت و خطی که از محل برخورد این دایره با محور عمودی ساخته میشود، محور کتانژانت نامیده میشوند. از آنجایی که شعاع دایره مثلثاتی واحد یا یک است، اندازه سینوس و کسینوس در فاصله $$[-1,1]$$ قرار میگیرند ولی تانژانت و کتانژانت ممکن است از منفی بینهایت تا مثبت بینهایت تغییر کنند. در این بین یک مثلث در داخل دایره مثلثاتی دیده میشود که براساس آن نسبتهای سینوس و کسینوس محاسبه شده و همچنین در خارج از آن نیز مثلثی قرار دارد که نسبتهای تانژانت و کتانژانت را میسازد.
به این نکته نیز توجه داشته باشید که واحد اندازهگیری زاویه ممکن است برحسب رادیان (Radian) یا درجه (Degree) صورت گیرد. در تصویر زیر جدولی را مشاهده میکنید که مقدار نسبتهای مثلثاتی (سینوس، کسینوس، تانژانت و کتانژانت) را برحسب رادیان و درجه نشان میدهد (جدول سینوس کسینوس). همانطور که مشخص است، زاویههایی که واحد اندازهگیری آنها برحسب رادیان است، بر اساس نسبتی از عدد پی ($$\pi$$) شناخته و نوشته شدهاند.

نکته: معمولا درجه را به عنوان واحد اندازهگیری زاویه در نظر گرفته و رادیان را طول کمانی در نظر میگیرند که برابر با شعاع دایره مثلثاتی (یعنی یک واحد) است.
حال که با نسبتهای مثلثاتی و نحوه اندازهگیری زاویه آشنا شدید، به توابع مرتبط با زاویه و نسبتهای مثلثاتی در اکسل خواهیم پرداخت.
تبدیل واحدهای اندازهگیری زاویه در اکسل
فرض کنید زاویه $$\theta$$ برحسب درجه به شما داده شده و میخواهید آن را به رادیان تبدیل کنید. برای انجام این کار در اکسل از تابع RADIANS استفاده میکنیم. شکل دستوری این تابع در ادامه دیده میشود.
$$ \large RADIANS(angle) $$
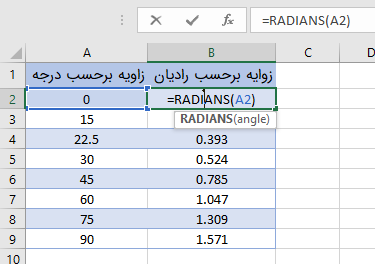
مشخص است که پارامتر این تابع یعنی angle همان زاویه برحسب درجه است. به این ترتیب میتوانیم زاویههای اندازهگیری شده با مقیاس درجه را به مقیاس رادیان تبدیل کنیم. در تصویر زیر چنین محاسباتی صورت گرفته است که در آن زاویههای معروف برحسب درجه مانند ۰، ۱۵، ۲۲٫۵، ۳۰، ۴۵، ۶۰، ۷۵ و ۹۰ به رادیان تبدیل شدهاند.
عکس این عمل نیز امکانپذیر است به این معنی که به کمک یک تابع در اکسل میتوانیم زاویه برحسب رادیان را به درجه تبدیل کنیم. در این حالت باید از تابع DEGREE استفاده کرده و پارامتر آن را مقدار زاویه برحسب رادیان انتخاب کنیم. در تصویر زیر چنین محاسباتی صورت گرفته است که اینبار زاویههای معروف برحسب رادیان به درجه تبدیل شدهاند.
نکته: از آنجایی که زاویه برحسب رادیان باید برحسب نسبتهایی از مقدار عدد پی ($$\pi$$) باشد، در ستون A، زاویهها را به کمک تابع ()PI در اکسل، مشخص کردهایم.
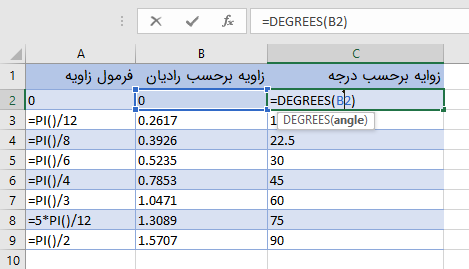
همانطور که مشاهده میکنید این زاویهها با جدولی که در تصویر ۱ نشان داده شده، مطابقت دارند. حال که تغییر واحد اندازهگیری زاویهها را فرا گرفتید، میتوانیم توابع مثلثاتی در اکسل را معرفی کنیم.
تابع سینوس و کسینوس در اکسل
خوشبختانه یا متاسفانه، اکسل برای محاسبه نسبتهای مثلثاتی از مقیاس رادیان استفاده میکند. البته این امر به صورت یک استاندارد در بین بیشتر برنامههای کاربردی رایانهای وجود دارد. در نتیجه اگر میخواهید مقدار سینوس و کسینوس و دیگر نسبتهای مثلثاتی را محاسبه کنید، باید زاویه برحسب درجه را به رادیان تبدیل کنید.
برای محاسبه مقدار سینوس یک زاویه از تابع SIN استفاده میشود. شکل دستوری این تابع به صورت زیر است:
$$ \large SIN(number) $$
مشخص است که پارامتر number، همان زاویه برحسب رادیان است. نحوه محاسبه کسینوس زاویه نیز به همین شکل خواهد بود و فقط کافی است از تابع COS استفاده کنید.
$$ \large COS(number) $$
به تصویر زیر توجه کنید که در آن مقدار سینوس و کسینوس برای زاویههای معمول محاسبه شده است. واضح است که این مقادیر با جدول مربوط به تصویر ۱ نیز مطابقت دارند. به یاد دارید که واحد اندازهگیری زاویه به کار رفته برای محاسبه این نسبتها برحسب رادیان است.
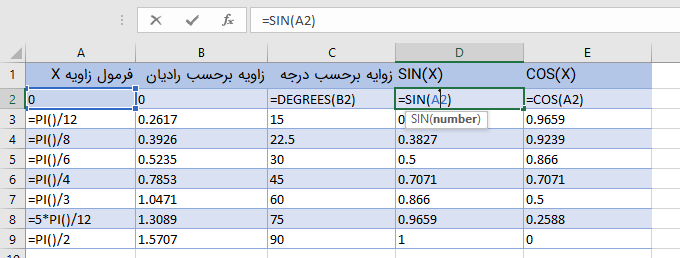
البته میتوانستید با ترکیب تابع SIN یا COS با تابع RADIANS، برای زاویههایی که برحسب درجه هستند نیز محاسبات را انجام دهید. برای مثال فرض کنید بخواهیم مقدار زاویه برحسب درجه را در یک سلول وارد کرده و مقدار سینوس آن را در سلول دیگری محاسبه کنیم. در این صورت تابع مورد نظر به شکل ترکیبی از دو تابع RADIANS و SIN خواهد بود. فرض کنید که در اینجا مقدار سلول A1 همان زاویه برحسب درجه است.
$$ \large SIN(RADIANS(A1)) $$
البته همین کار را هم برای COS میتوان انجام داد.
$$ \large COS(RADIANS(A1)) $$
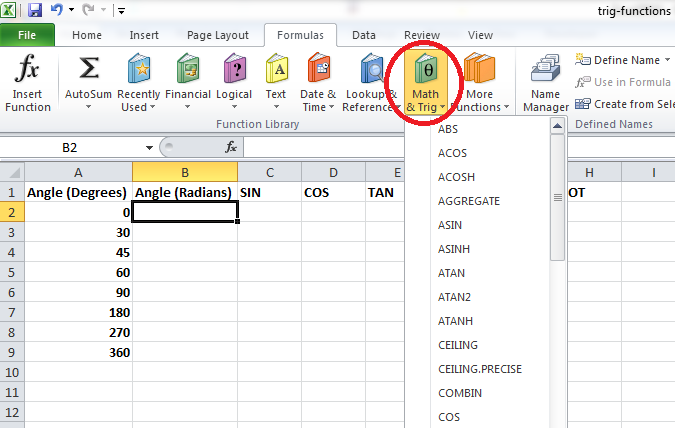
نکته: برای دسترسی به توابع مثلثاتی در اکسل میتوانید به جای تایپ کردن نام آنها، از برگه Formula و قسمت Function Library گزینه Math and Trig را انتخاب کنید.
تابع تانژانت و کتانژانت در اکسل
قواعدی که برای بدست آوردن سینوس و کسینوس زاویهها گفته شد، برای تانژانت و کتانژانت هم صادق است به این معنی که باید زاویهها برحسب رادیان باشند. برای محاسبه تانژانت و کتانژانت زاویه در اکسل از تابع TAN و COT استفاده میکنیم. شکل دستوری این توابع به صورت زیر است:
$$ \large TAN(number) $$
$$ \large COT(number) $$
واضح است که پارامتر number باید مقداری برحسب رادیان باشد. در تصویر زیر مقدار تانژانت و کتانژانت زاویههای مختلف محاسبه و نمایش داده شده است.
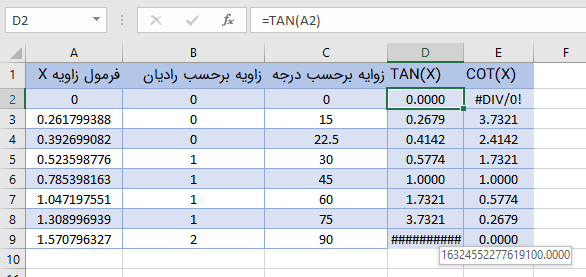
همانطور که در تصویر 2 مشاهده میکنید، برای زاویه ۹۰ درجه یا $$\pi/2$$، مقدار تانژانت برابر با بینهایت است. در اینجا هم اکسل با بزرگترین عددی که ممکن است، مقدار تانژانت را نشان داده است. البته با توجه به اینکه در سلول A9 مقدار زاویه برحسب رادیان با استفاده از تابع ()PI محاسبه شده است، دقت در محاسبه تابع تانژانت، بستگی به تابع ()PI نیز دارد. اکسل این عدد را با دقت ۱۵ رقم اعشار در حافظه خود نگه داشته است. از طرفی با توجه به رابطه معکوسی که بین تانژانت و کتانژانت برقرار است، مقدار کتانژانت برای زاویه صفر رادیان، بینهایت شده که در اینجا با علامت خطای !DIV/0 # نشان داده شده، چون برای محاسبه آن، مقدار تانژانت عکس شده که منجر به خطای تقسیم بر صفر در اکسل خواهد شد.
تابع معکوس سینوس و معکوس کسینوس در اکسل
اکسل علاوه بر محاسبه توابع مثلثاتی، میتواند معکوس این نسبتهای مثلثاتی را هم بدست آورد. این امر مثلا برای معکوس سینوس، پیدا کردن زاویهای (برحسب رادیان) است که سینوس آن با مقدار مشخصی برابر شده است. برای کسب اطلاعات بیشتر در این زمینه میتوانید نوشتار تابع معکوس مثلثاتی — به زبان ساده را مطالعه کنید.
برای محاسبه معکوس سینوس و معکوس کسینوس در اکسل باید به ترتیب از توابع ASIN و ACOS استفاده کنیم. شکل دستوری این توابع نیز به صورت زیر است.
$$\large ASIN(number)$$
$$\large ACOS(number)$$
پارامتر این توابع که با number مشخص شده، همان مقدار سینوس یا کسینوس است. پس باید مقداری در بازه $$[-1,1]$$ باشد. بنابراین اگر مقداری خارج از این محدوده برای تابع ASIN یا ACOS مشخص کنید، اکسل نتیجه را به صورت خطای !NUM# نشان میدهد. از طرفی نتیجه تابع ASIN و ACOS نیز در فاصله $$[-\pi,\pi]$$ یعنی تقریبا حدود ۳٫۱۴۱۵- تا ۳٫۱۴۱۵ قرار خواهد گرفت.
در تصویر زیر نحوه استفاده از تابع ASIN مشاهده میشود.
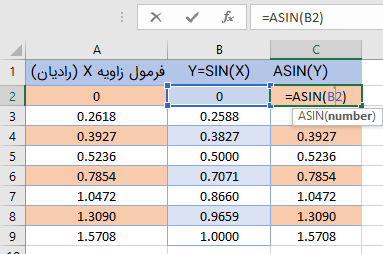
همانطور که مشاهده میکنید، مقدار زاویه (برحسب رادیان) برای مقادیر مربوط به ستون B در ستون C، محاسبه شده است. این مقادیر درست برابر با اندازه زاویههایی است که در ستون A نوشته شده است.
نکته: نام تابع ASIN، مخفف نام Arc SIN یا آرک سینوس است. آرک در اینجا به کمانی اشاره دارد که مقدار سینوس زاویه مربوط به آن، برابر با پارامتر تابع ASIN است.
همین محاسبات را برای تابع ACOS نیز میتوان انجام داد. اجرای این تابع و حاصل محاسبات را در تصویر 9 میتوان دید.
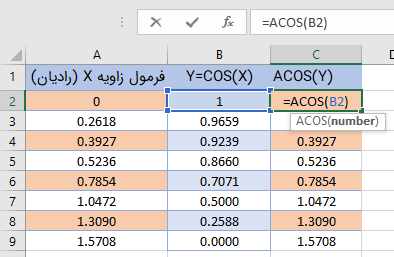
نکته: توجه داشته باشید که تابع معکوس سینوس و کسینوس با معکوس تابع سینوس و کسینوس تفاوت دارد. اگر هر یک از توابع مثلثاتی مثل SIN یا COS حتی TAN را به صورت کسر معکوس درآوریم بطوری که صورت کسر برابر با ۱ و مخرج کسر هر یک از توابع مثلثاتی باشد، نتیجه را معکوس تابع مثلثاتی میگویند. به این ترتیب معکوس تابع سینوس را «کسکانت» (با نماد CSC) و معکوس تابع کسینوس را «سکانت» (با نماد SEC) و معکوس تابع تانژانت را «کتانژانت» (با نماد Cot) نشان میدهند.
برای معکوس توابع مثلثاتی نیز در اکسل توابعی در نظر گرفته شده است. جدول زیر به معرفی این گونه توابع پرداخته است. البته توجه دارید که زاویه برای این توابع نیز باید برحسب رادیان مشخص شده باشد.
| نماد | شرح | محاسبه |
| CSC | محاسبه کسکانت (معکوس سینوس) یک زاویه | $$ CSC(x)=\dfrac{1}{SIN(X)} $$ |
| SEC | محاسبه سکانت (معکوس کسینوس) یک زاویه | $$ SEC(X) = \dfrac{1}{COS(X)} $$ |
| COT | محاسبه کتانژانت (معکوس تانژانت) یک زاویه | $$ COT(X) = \dfrac{1}{TAN(X)} $$ |
در تصویر 10 برای چند زاویه مهم مقدار معکوس توابع مثلثاتی مشخص شده است.
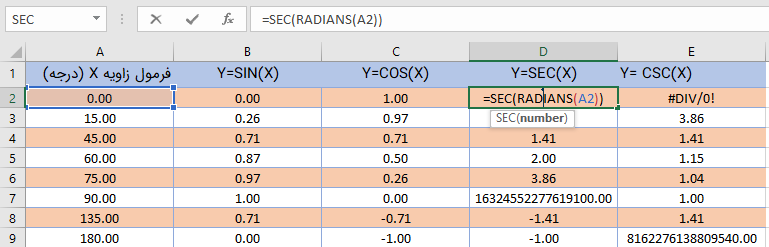
تابع معکوس تانژانت و کتانژانت در اکسل
درست به همان شکلی که توابع معکوس برای سینوس و کسینوس تعریف میشود، تابع معکوس تانژانت و تابع معکوس کتانژانت نیز وجود دارند. کافی است از تابع ATAN و ACOT استفاده کنید. در تصویر زیر نتیجه اجرای محاسبات توسط این دو تابع برای مقادیر مختلف دیده میشود.
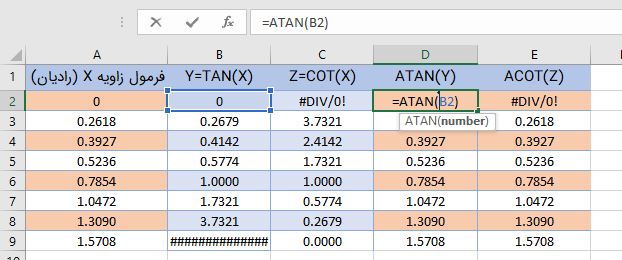
نکته: هر چند مقدار تانژانت و کتانژانت کران بالا یا پایین ندارند، ولی مقدار تابع ATAN و ACOT برحسب رادیان بوده و در بازه $$[-\pi,\pi]$$ یعنی تقریبا حدود ۳٫۱۴۱۵- تا ۳٫۱۴۱۵ قرار خواهند گرفت.
رسم نمودار توابع مثلثاتی در اکسل
در این قسمت با استفاده از توابع مثلثاتی در اکسل برای زاویههای ۰ تا $$\pi$$ مقادیر نسبتهای مثلثاتی را محاسبه کرده و به صورت یک نمودار منحنی، ترسیم میکنیم تا روند تغییرات این توابع نسبت به زاویهها، بهتر دیده شود.
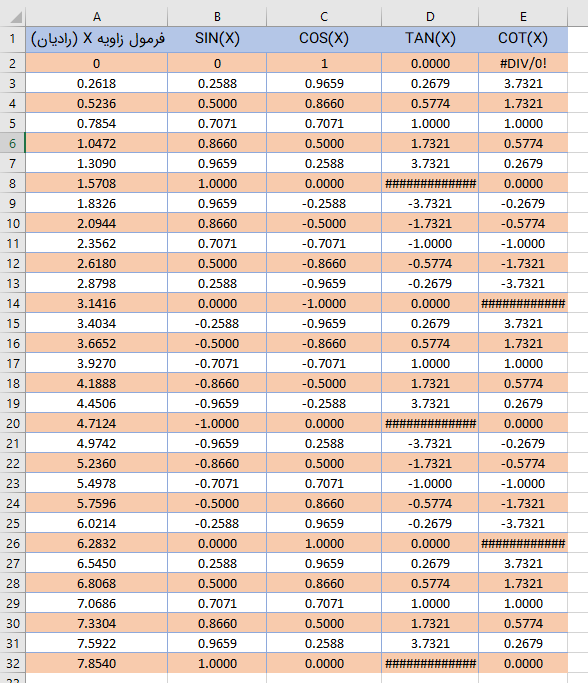
ابتدا باید جدولی از زاویهها و نسبتها ایجاد کنیم و سپس نمودار را ترسیم کنیم. این کار براساس تصویر 12 صورت گرفته است. حال براساس این جدول، نمودار را ترسیم میکنیم.
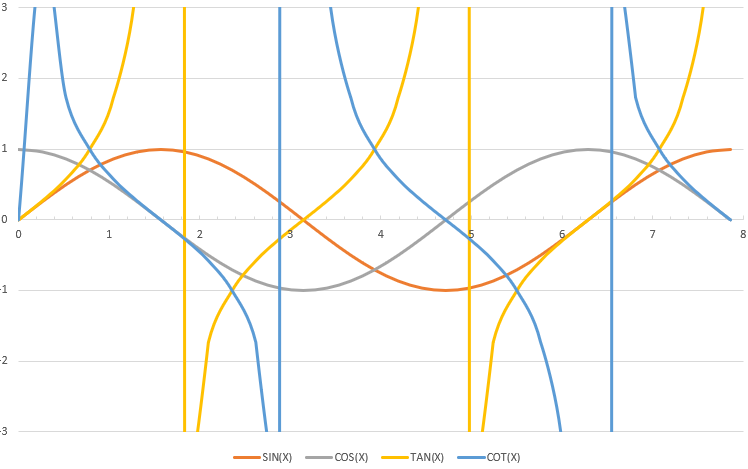
از آنجایی که مقادیر توابع مثلثاتی به صورت دورهای تکرار میشوند، نمودارها نمایش داده شده در تصویر ۱۳، به صورت تکراری ترسیم شدهاند زیرا توابع مثلثاتی متناوب هستند.
خلاصه و جمعبندی
در این نوشتار با نحوه محاسبه توابع مثلثاتی در اکسل آشنا شدید. مشخص شد که همه توابع مثلثاتی برحسب زاویه با واحد گرادیان بدست میآیند. بنابراین باید ابتدا زاویههای برحسب درجه را به رادیان تبدیل کرده، سپس نسبتهای مثلثاتی را برایشان محاسبه کنیم. همچنین برای محاسبه معکوس توابع مثلثاتی در اکسل نیز راهکارهایی ارائه کردیم. در انتها نیز به کمک نموداری که توسط اکسل ترسیم شد، ارتباط بین زاویهها و نسبتهای مثلثاتی را به صورت تصویری، قابل درک کردیم.
اگر این مطلب برایتان مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای نرمافزار اکسل
- آموزش ریاضی پایه دانشگاهی
- مجموعه آموزشهای ریاضیات
- تفریق در اکسل — از صفر تا صد
- ضرب در اکسل -- از صفر تا صد
^^










