کریستالوگرافی چیست؟ — بلورشناسی و بلورنگاری به زبان ساده
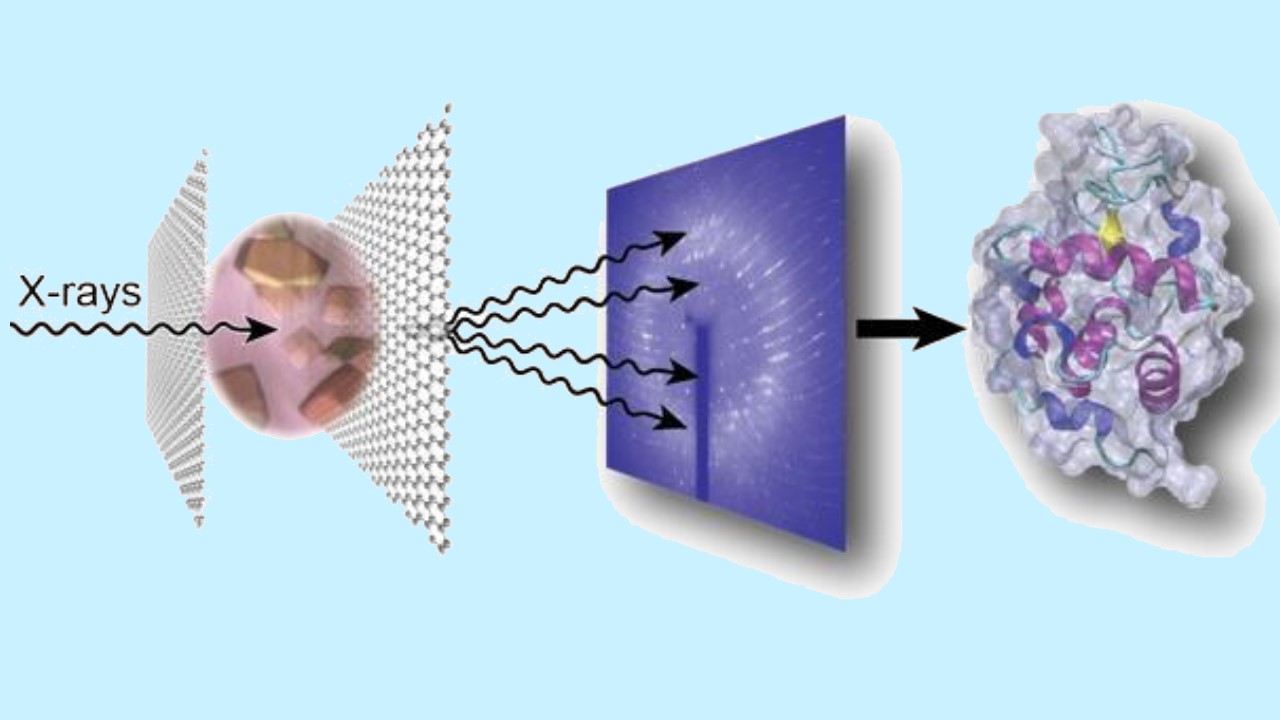
کریستالوگرافی یا بلورشناسی شاخهای از علم و مهندسی مواد است که با نحوه چینش اتمها و پیوند میان آنها در جامدهای بلوری متناسب با ساختار هندسی اتمها سر و کار دارد. کریستالوگرافی موضوعی پراهمیت است زیرا به واسطه آن میتوان به خواص و ویژگیهای مواد پی برد و با کمک علم بلورشناسی میتوان مدلهای ساختاری اتم را درک کرد. همچنین به کمک ساختار اتمها بسیاری از خواص فیزیکی یا شیمیایی مواد قابل توجه است. در این مطلب برای اینکه یاد بگیرید منظور از کریستالوگرافی چیست مفاهیم پایه و اساسی در رابطه با آن توضیح داده شده است.
کریستالوگرافی چیست ؟
زمانی که مواد جامد طبقهبندی میشوند دو موضوع اهمیت بسیار بالایی دارند که یکی نوع پیوند است. به عبارتی اینکه نحوه اتصال اتمها باهم چگونه است و موضوع بعدی این است که اتمها چگونه در کنار هم قرار میگیرند به عبارتی نظم و ترتیب قرارگیری اتمها به چه نحوی است. پس به طور کلی میتوان گفت که دو محور اصلی کریستالوگرافی عبارتند از:
- پیوند بین اتمها
- آرایش اتمها در کنار هم
آرایش اتمها در ساختارهای کریستالی جامد میتواند به دو دسته منظم و بینظم تقسیمبندی شود.
منظم (Ordered)
آرایش اتم به صورت منظم به این معناست که هر نقطه از ساختار یک چیدمان دارد. به عبارتی آرایش اتمها تکرار میشود و این تکرار چیدمان تا مسیرهای طولانی ادامه پیدا میکند. بنابراین از مشخصههای مهم چیدمان منظم «نظم بلند دامنه» (Long range order) در بلور است. در این حالت است که ماده جامد از نوع کریستالی خواهد بود و میگوییم ساختار ماده مورد نظر کریستالی است. یکی از مثالهای بارز برای جامدهای کریستالی منظم، جامد بلوری سدیم کلرید یا همان نمک طعام است. در تصویر زیر میتوانید ترتیب قرارگیری اتمهای سدیم و کلر را در بلور نمک طعام مشاهده کنید.

بینظم
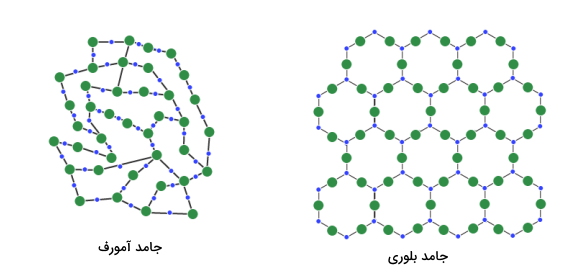
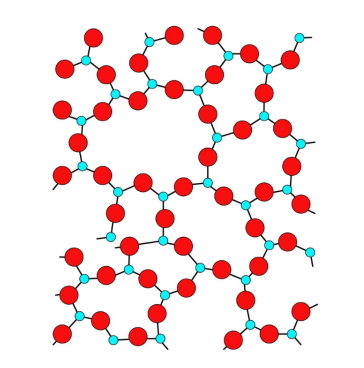
در مقابل جامدهای کریستالی منظم، مواد جامدی وجود دارند که در اتمها در ساختار آنها در وضعیت منظمی قرار نگرفتهاند و آرایش آنها بینظم است. البته ممکن است در برخی از نقاط ماده ساختاری منظم داشته باشند اما برآیند کلی بینظم است. در واقع ترتیب قرارگیری اتمها با نظم مشخصی تکرار نمیشود به عبارتی اتمها به صورت تصادفی در کنار هم قرار میگیرند. از مشخصههای مهم این مواد «نظم کوتاه دامنه» (short range order) است و به آنها جامد بیشکل یا شیشه میگویند. دلیل اینکه به جامدات «بیشکل» (Amorphous) موادی با حالت شیشهای یا به صورت کلی شیشه میگویند این است که در ساخت شیشهها مواد اولیه و خام را تا یک دمایی بالا میبرند.
سپس به طور ناگهانی دمای آن را تا دماهای پایین میرسانند، به همین دلیل فرایند انجماد از دمای بسیار بالا به دمای بسیار پایین کاملا ناگهانی و بدون زمان دادن صورت میگیرد. بنابراین اتمها فرصت کافی برای آرایش و چیدمان منظم ندارند یعنی اتمها به صورت بینظم در کنار هم قرار میگیرند. به همین دلیل به موادی که چینش اتمها در ساختار آنها بینظم است جامد بیشکل میگویند.
کریستال چیست ؟
برای اینکه متوجه شویم کریستالوگرافی چیست اولین راه بررسی لغوی این نام است. در واقع اینکه بدانیم نام کریستال از چه کلمهای ریشه گرفته و به چه به معناست درک مطلب کریستالوگرافی را برایمان خیلی راحتتر میکند. واژه «کریستال» (Crystal) در کریستالوگرافی از یک واژه یونانی (Krystallos) به معنای «یخ» ریشه گرفته است. در ساختار یخ همانطور که در شکل زیر نشان داده شده دانههایی به شکل برف وجود دارد که درواقع کریستالیت یا بلورک هستند.

البته همه مواد کریستالی قاعدتا به شکل یخ نیستند اما به طور کلی دلیل استفاده از این نام بخاطر این بود که اولین بار به این شکل نام کریستال شکل گرفت. در طبیعت، بلورهای سنگ به راحتی پیدا میشوند و اگر به شکل زیر نگاه کنید متوجه خواهید شد که بلورهای سنگی تا حدی به یخ شباهت دارند. به همین خاطر در عصر باستان مردم گمان میکردند که این بلورهای سنگی به دلیل منجمد شدن در سرما به وجود آمدهاند. اما اکنون با پیشرفت علم میدانیم که این بلورهای سنگی در اثر حرارت و فشار به وجود میآیند. بلورهای سنگی بیرنگ نوعی از یک کانی به نام کوارتز هستند که این کانی از سیلیس با ترکیب شیمیایی تشکیل شده است.

در طبیعت، شکلهای مختلفی از کانیهای کوارتز وجود دارد که هر یک از آنها رنگهای گوناگونی دارند. در تصویر زیر سه نمونه از انواع کوارتزهای رنگی را میتوان دید. تصویر اول (سمت چپ) مربوط به آمتیست یعنی فراوانترین نوع کانی کواتز است. رنگ این نوع از کانی به دلیل حضور یونهای فلز آهن در ترکیب با پرتوهای اشعه ایکس یا گاما است. اگرچه در مورد جزئیات اصلی و دقیق ساختاری که باعث ایجاد این رنگ میشود هنوز اطلاعاتی وجود ندارد. جالب است که بدانید رنگ آمتیست زمانی که در معرض پرتوهای خورشید قرار میگیرد به سرعت محو میشود.

در کوارتز بیرنگ یا سفید شیری هیچ یون فلزی وجود ندارد، اما اجزای کوچکی از قطرههای مایع و / یا شکافهایی وجود دارد که نور را پراکننده می کنند و سبب میشود رنگ آن به صورت سفید شیری درآید. تصویر سمت راست مربوط به کوارتز صورتی یا «گل سرخ» (Rose Quartz) است و در دو نوع مات و شفاف وجود دارد. بر اساس تحقیقاتی که بر روی این سنگ معدنی صورت گرفته مشاهده شده که رنگ صورتی مات در کوارتز صورتی به دلیل وجود اجزای معدنی خارجی به نام دومورتریت است که از مینرال سیلیکات بور آلومینیوم تشکیل شده است و در اثر ترکیب آهن با تیتانیوم رنگ صورتی کوارتز را تیره میکند. از طرف دیگری رنگ کوارتز صورتی شفاف به دلیل برهمکنش میان آلومینیوم در گروه ۱۳ با فسفر در گروه ۱۵ در اثر ترکیب با پرتوهای تشعشع یونی (اغلب ایزوتوپ پتاسیم-۴۰) است.
کریستالوگرافی اشعه ایکس
کریستالوگرافی اشعه ایکس ابزاری است که از آن برای تعیین ساختار اتمی و مولکولی بلور استفاده میشود. اتمهای بلور باعث میشوند که پرتو اشعه ایکس به هنگام عبور از آنها در جهات بسیاری پراکنده شود که در تصویر زیر نشان داده شده است. با محاسبه زاویه پراش و شدت این پرتوها، بلورشناس میتواند یک تصویر سهبعدی را از چگالی الکترون در میان بلور به دست بیاورد. از طریق این تصویر میانگین موقعیتهای قرارگیری اتمها در بلور، پیوندهای شیمیایی (فازها)، نظم ساختاری و بسیار از اطلاعات دیگر مشخص میشود. این روش، ساختار و عملکرد بسیاری از مولکولها را اعم از مولکولهای بیولوژیکی شامل ویتامینها، داروها، پروتئینها و اسیدهای هستهای مانند DNA مشخص میشود.
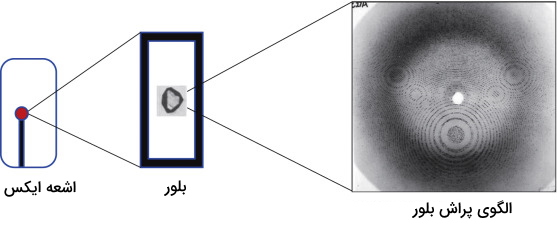
بنابراین به طور خلاصه میتوان گفت که «کریستالوگرافی یا بلورنگاری دانشی است که به کمک عبور اشعه ایکس از جامدهای بلوری میتوان به طرز آرایش اتمها در فضاهای سهبعدی پی برد». برای استفاده از این آنالیز حتما باید نمونه مورد نظر، جامد بلوری باشد تا آرایش منظم اتمها بتوانند پرتوهای اشعه ایکس تابیده شده را پراش کنند. سپس با استفاده از یک سری روابط ریاضی از جمله قانون براگ که مهمترین آن هاست الگوی پراش به دست میآید. آنالیز پراش «پرتو ایکس» (X-ray Diffraction| XRD) در این سالها به یک آنالیز و ابزار قدرتمند جهت بررسی نحوه آرایش اتمها، پیوند میان ترکیبات بلوری، فاصله بین صفحات، کرنش شبکه و غیره برای دانشمندان تبدیل شده است.
نقش قانون براگ در کریستالوگرافی اشعه ایکس چیست ؟
پراش اشعه ایکس زمانی رخ میدهد که نور با ابر الکترونی اطراف هسته اتمهای جامد بلوری برهمکنش خواهند داشت. با توجه به ساختار متناوب بلوری جامد، میتوان آن را به عنوان مجموعهای از صفحات با فاصلههای مشخص و برابر از هم در نظر گرفت. سوال اینجاست که پرتو ایکس با چه زاویهای به سطح کریستال برخورد میکند؟ برخی از پرتوهای نور در همان زاویه از جامد کریستالی پراکنده میشوند. باقیمانده نور به داخل کریستال میرود و مابقی با صفحههای ثانویه اتم برهم کنش پیدا میکنند. برخی از پرتوهای نور نیز با زاویه تتا پراکنده میشوند و مابقی نور به عمق جسم جامد کریستالی میرود. این فرایند برای بسیاری از صفحهها در کریستال تکرار میشود.
پرتوهای اشعه ایکس قبل از برخورد با صفحات کریستال، مسیرهایی با طول های مختلف را طی میکنند. بنابراین بعد از برهمکنش در صورتی پرتوها برهمکنش سازنده خواهند داشت که اختلاف طول مسیر برابر تعداد صحیحی از طول موجها باشد. در تصویر زیر اختلاف طول مسیر پرتو برخوردکننده با صفحه اول و همچنین پرتو برخوردکننده با صفحه دوم برابر با است. بنابراین تنها در صورتی که رابطه برقرار باشد دو پرتوی پراش تداخل سازنده (در همان فاز) خواهند داشت.
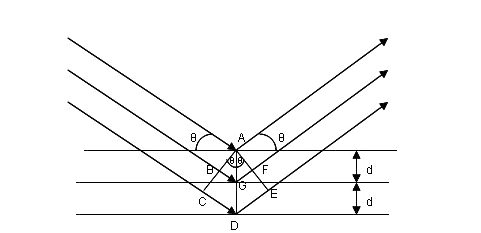
طبق روابط مثلثاتی داریم از طرفی بنابراین با مرتب کردن این رابطه به رابطه زیر میرسیم:
پس با جایگذاری مقادیر در رابطه خواهیم داشت:
این رابطه به افتخار دو دانشمند «ویلیام هنری براگ» (William Henry Bragg) و پسرش «ویلیام لورنس براگ» (William Lawrence Bragg) به دلیل تحلیل ساختارهای بلوری توسط اشعه ایکس به نام «قانون براگ» (Bragg's Law) نامگذاری شده است.
در رابطه براگ
- : عدد صحیحی بوده که مرتبه پراش را نشان میدهد.
- : طول موج پرتویی است که با اتمهای جامد بلوری برهمکنش پیدا میکند.
- : زاویهای است که پرتو از سطح کریستال پراش میکند.
- : فاصله بین صفحات است.
مواد آمورف چه موادی هستند ؟
همان طور که در دو قسمت قبلی توضیح دادیم نقطه مقابل کریستالها یا بلورها مواد بیشکلی وجود دارند که در این نوع از جامدات، اتمها در ساختار کریستالی خود نظم مشخصی ندارند. ازجمله این مواد میتوان به موارد زیر اشاره کرد:
- چوب
- شیشه
- پلاستیک
- و غیره
به این مواد و سایر موادی که اتمها بدون هیچگونه نظمی قرار گرفتهاند، آمورف یا جامد بیشکل میگویند. ممکن است در نگاه اول این موضوع برایتان عجیب به نظر برسد زیرا با خود فکر میکنید که موادی مانند مواد نامبرده شده در بالا ازجمله چوب یا شیشه از شکل خاصی برخوردارند. اما باید بدانید مفهوم آمورف در علم کریستالوگرافی مربوط به ساختار داخلی مواد و شکل قرارگیری اتمهاست که در این نوع مواد اتمها شکل قرارگیری خاصی ندارند به عبارتی بهطور تصادفی و بدون هیچ الگوی خاصی در کنار هم آرایش دارند.
به طور کلی حالتهای فیزیکی مواد بسته به نوع چیدمان و آرایش اتمها در ساختار به سه حالت جامد، مایع و گاز تقسیمبندی میشوند. خود حالت جامد به دو شکل کلی کریستالی (بلوری) و بی شکل تبدیل میشود. از آنجا که علم کریستالوگرافی با بلورها سر و کار دارد در این مطلب به بررسی جامدات کریستالی میپردازیم. به طور کلی در کریستالوگرافی با یک سری مفاهیم اولیه و اساسی سر و کار داریم که در ادامه به توضیح هر یک از آنها می پردازیم. این مفاهیم اولیه و پایه در کریستالوگرافی عبارتند از:
- سلول واحد
- تقارن
- دستگاههای کریستالی
- شبکههای براوه
- شبکه و موتیف
- آنیزوتروپی
- فاکتور فشردگی اتمی
سلول واحد در بلورنگاری چیست ؟
تا این قسمت یاد گرفتیم که در تمام نقاط جامد کریستالی نظم قرارگیری اتمها به صورت یک روند تکرار شدنی در ساختار ماده تکرار میشود. اگر ساختار هندسی جامدهای کریستالی را به کوچکترین قسمت تقسیم شود به گونهای که تقارن، نظم و خواص ساختار کل ماده را در بربگیرد، به این قسمت انتخاب شده «سلول واحد» میگویند. در واقع اگر همه قسمتهای کوچک یا همان سلول واحد را در کنار هم قرار دهیم کل ساختار ماده به دست میآید.
برای اینکه با مفهوم سلول واحد بیشتر آشنا شوید به تصویر زیر نگاه کنید. تصویر زیر مربوط به یکی از نقاشیهای «اشر» (Escher) است. اگر به خوبی نگاه کنید خواهید دید که اردکها با یک نظم خاصی در سراسر نقاشی تکرار میشوند که در تصویر با کادر رنگی مشخص شده است. به این واحد تکرار شونده اردکها در تصویر سلول واحد میگویند و دقیقا همین اتفاق برای اتمها نیز در ساختار ماده میافتد.
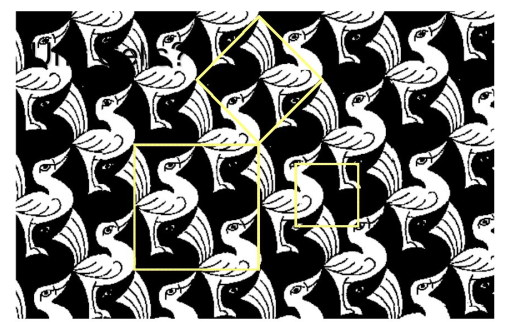
در تصویر فوق واحدهای تکرارشونده برای اردکها میتواند مربع کوچک، مربع بزرگ و لوزی باشد. به هر کدام از این واحدهای تکرار شونده سلول واحد میگویند.
در واقع میتوان گفت که سلول واحد نماینده کل ساختار ماده است. به طور کلی برای سلول واحد دو قانون کلی وجود دارد که باید برای آن صدق کند، این دو قانون عبارتند از:
- فقط واحدهای سازنده مواد که با یک ترتیب خاص در سراسر ساختار ماده تکرار میشوند باید به عنوان سلول واحد در نظر گرفته شوند.
- تنها یک نوع سلول واحد میتواند برای حجم عنصر در نظر گرفته شود (به عنوان مثال در تصویر فوق فقط یک سلول واحد می تواند در نظر گرفته شود).
در تصویر زیر سه نوع مکعبمربع (Cubic) اورده شده است. حال سوال پیش میآید که این مکعب بزرگ از لحاظ ساختار هندسی چگونه باید به بخشهای کوچکتر تقسیم شود؟ یک مکعب بزرگ را به چیزی جز مکعبهای کوچک نمیتوان تقسیم کرد. در اثر تقسیم کردن این مکعب به مکعبهای کوچک در نهایت به یک مکعب کوچک میرسیم که این مکعب همان سلول واحد است. یک مکعبمربعتوسط مشخصههایی مانند طول، عرض و ارتفاع و زاویههای میان آنها تعریف میشود.
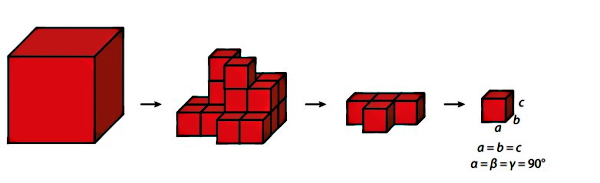
البته این تنها حالتی نیست که بتوان به کمک آن یک مکعب را به قسمتهای کوچکتر تبدیل کرد. همانطور که در دو تصویر زیر نشان داده شده است مکعب به صورت افقی یا عمودی هم میتوان برش بخورد و به قسمتهای کوچکتر تقسیم شود. در حالتی که مکعب به صورت افقی برش داده شود و به مکعب کوچکتر تقسیم شود صفحات مربعی را به وجود میآورند که در این حالت نیز همه زاویهها عمود بر هم هستند اگرچه در این حالت سطوح مربعی شکل هستند و کنارهها شکل مستطیل دارد به عبارتی سلول واحد دیگر مکعبمربعنیست و در این حالت سلول واحد مکعب مستطیل است.
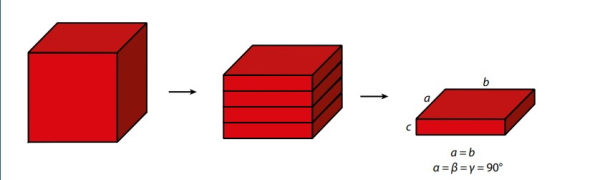
در حالتی که مکعبمربعمانند تصویر زیر از ناحیه عمودی برش داده شود یک مکعب مستطیل به وجود میآید یعنی در این حالت تمام ضلعها با هم تفاوت دارند.
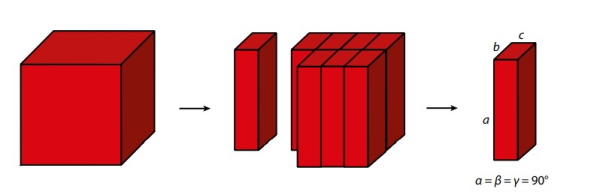
بنابراین یک مکعب مربعی را میتوان در سه حالت به واحدهای کوچکتری تقسیم کرد که در هر سه حالت مشخصههای ساختاری هندسی با هم متفاوت هستند. البته لازم به ذکر است که در تمامی موارد فوق تعداد وجهها برابر ۶ است. تمامی اطلاعات بالا به صورت خلاصه در جدول زیر گردآوری شده است.
| حالت تقسیم کردن مکعب | ابعاد | زاویهها |
| مکعبهای کوچک | ||
| افقی | ||
| عمودی |
خالی از لطف نیست که برای اینکه بیشتر با مفهوم سلول واحد در کریستالوگرافی آشنا شوید مثال دیگری بزنیم. در این حالت شکل ساختار اولیه یک شش ظلعی خواهد بود که میتواند به دو صورت ستونهای ششضلعی یا منشور تقسیم شود. اما در این مثال برخلاف مثال قبلی، منشور ششضلعی شامل ۸ وجه خواهد بود. همچنین ممکن است که خود منشور به قسمتهای کوچکتری تقسیم شوند که معمولا در این حالت شامل ۶ وجه است.
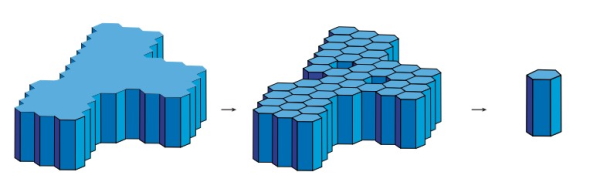
حال این سوال پیش میآید که در حالتی که خود منشور به قسمتهای کوچکتری تقسیم شود آیا با جمعآوری آنها ساختار اولیه به دست خواهد آمد؟ در حقیقیت برای پاسخ به این سوال دو احتمال وجود دارد که در شکل زیر نشان داده شده است. در اولین حالت ستونهای هگزاگونال از ناحیه محوری که طول زیادی دارد به دو نیمه برش داده میشوند که در نتیجه این برش یک مثلث متساویالساقین به عنوان قاعده به وجود میآید. در حالت دوم برش، ستون هگزاگونال به ۳ قسمت مساوی تبدیل می شود که باعث ایجاد تشکیل بلوکهای کوچک به عنوان قاعده میشوند. در این حالت طول لبهها باهم برابرند و زاویه بین آنها برابر ۱۲۰ درجه است.
اکنون که این دو حالت را بررسی کردیم باید بببینیم کدام یک از این دو حالت به عنوان سلول واحد ترجیح داده میشوند؟ برای پاسخ به این سوال باید دو جنبه را بررسی کنیم:
- در حالت اول، شکل هندسی ایجاد شده سه نوع وجه متفاوت دارد. در واقع ساختار جدید به دست آمده شامل ۶ وجه است که در بین این ۶ وجه، دو وجه بالا و پایینی با هم برابرند و به موازات هم قرار دارند. از چهار وجه جانبی سه وجه با هم برابر هستند و تنها جهتگیری آنها با هم متفاوت است. اما در نهایت اندازه وجه چهارم به طور کلی متفاوت است. در حالت دوم برش، ساختار هندسی ایجاد شده دو وجه متفاوت دارد (وجه بالا و پایینی و چهار طرف آن با هم برابرند که به موازات هم قرار گرفتهاند).
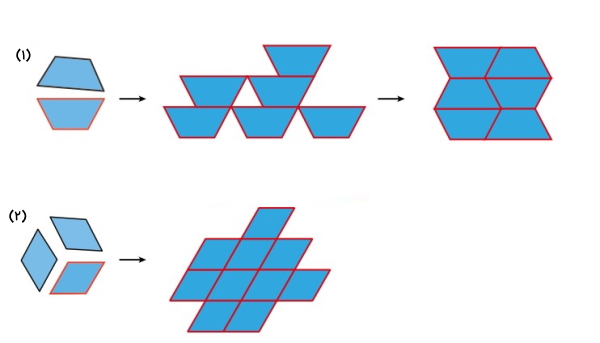
- باید به خاطر داشته باشیم که از کنار هم قرار گذاشتن این بلوکهای برش داده شده ساختار کلی ماده به دست میآید. بنابراین اگر بخواهیم دوباره شکل ساختار اولیه را از کنار هم قرار دادن بلوکهای حالت اول داشته باشیم (با در نظر گرفتن چینش بلوکها در یک جهت) این حالت امکانپذیر نخواهد بود زیرا فضاهای خالی همچنان باقی خواهد ماند. ساخت مجدد ساختار ماده تنها زمانی امکانپذیر خواهد بود که واحدهای کوچکتر دقیقا در دو جهتگیری مخالف نسبت به هم قرار گرفته باشند و این دقیقا تفاوت حالت اول با حالت دوم است. در حالت دوم با کنار هم قرار گرفتن واحدهای کوچک فضاهای خالی نیز پر میشوند و شکل واحد بزرگتر به دست میآید.
مشخصههای سلول واحد در کریستالوگرافی
بعد از اینکه مفهوم سلول واحد را در کریستالوگرافی یاد گرفتید نوبت به آشنایی با دو مشخصه اصلی سلول واحد میرسد.
متریک
سلول واحد در مرحله اول توسط مشخصهای به نام متریک مشخص میشود به این معنا که تمام پارامترهای شبکه باید توسط متریک مشخص شوند. ما دقیقا به شش پارامتر نیاز داریم تا یک سلول واحد را برایمان توصیف کند. از این فاکتورها سه تا از آنها متعلق به ابعاد طولی که با نامهای a، b و c شناخته می شوند هستند و هر کدام به ترتیب برای محورهای x، y و z هستند. همچنین سه فاکتور دیگر مربوط به زاویههای بین این ابعاد طولی هستند که با نامهای ، و شناخته میشوند. به این صورت زاویه آلفا بین یالهای b و c، زاویه بتا بین لبههای a و c و در نهایت زاویه گاما در بین a و b قرار میگیرد.
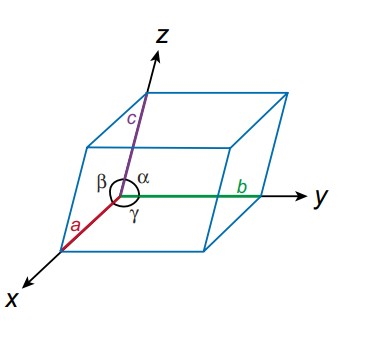
تقارن
ویژگی دیگر سلول واحد دقیقا از نام آن مشخص است زیرا سلول واحد شامل تقارن عنصرها در شبکه کریستالی است، بنابراین دومین ویژگی آن مربوط به تقارن خواهد بود. تقارن را میتوان به صورت زیر نیز تعریف کرد. بدین صورت که اگر شما یک قسمت از بلور را به عنوان سلول واحد در نظر بگیرید، به گونهای که شامل همه ویژگیهای سلول واحد باشد. بنابراین هر سه جهت را که در آن مشخص و سپس به هم وصل میکنید نباید هیچ عنصر متقارن اضافی در آن ظاهر شود.
اگر یک قسمت بزرگ از سلول واحد را انتخاب کنیم و متوجه حضور یک عنصر متقارن دیگری شویم یعنی انتخاب بخش تعیین شده به عنوان سلول واحد نادرست بوده است. بنابراین باید بخش کوچکتری را به عنوان سلول واحد در نظر بگیریم. به طور کلی در یک کلام میتوان گفت مفهوم تقارن به معنای انتخاب کوچکترین بخش ساختار ماده به عنوان سلول واحد است.
ساختار شیمیایی (استوکیومتری)
از تعریف سلول واحد یک ویژگی بسیار مهمی شکل میگیرد که این ویژگی در مورد ترکیب شیمیایی است (در واقع همان استوکیومتری است). ترکیب شیمیایی سلول واحد باید همانند ترکیب شیمیایی کل بلور باشد. به عنوان مثال ترکیب شیمیایی بلور یخ برابر با و نسبت عنصر هیدروژن به عنصر اکسیژن برابر ۲ به ۱ است. بنابراین در سلول واحد هم باید همین نسبت حفظ شود. اگر ما یک بخش از بلور را به عنوان سلول واحد در نظر بگیریم که نسبت هیدروژن به اکسیژن در آن برابر ۱ باشد (یعنی ترکیب برابر است) پس باید ترکیب شیمیایی کل بلور هم همین باشد.
به عبارتی امکان ندارد که ترکیب شیمیایی کل بلور و ترکیب شیمیایی سلول واحد دو ترکیب متفاوت از هم باشند. زیرا تنها موردی که برای سلول واحد صدق میکند این است که سلول واحد در هر سه جهت فضایی تکرار میشوند و این خاصیت شامل تغییر در نسبت عناصر تشکیلدهنده نیست. همچنین احتمال این وجود دارد که سلول واحد بیشتر از یک مولکول را در بر بگیرد. به عنوان مثال سلول واحد انتخابی مادهای دارای ۱۲ مولکول است اما این مسئله همچنان ارتباطی به تغییر در نسبت شیمیایی عناصر نسبت به هم ندارد.
معرفی ۷دستگاه کریستالی در بلور شناسی
در این قسمت به یکی از مهمترین مباحث مهم در کریستالوگرافی یعنی شبکه کریستالی میپردازیم. درواقع شبکه کریستالی همان سلول واحد است که در کل ساختار تکرار میشود. جالب است که بدانید تعداد شکلهای سلول واحد که توسط متریک آنها تعیین می شود بسیار محدود است. سلولهای واحد یا شبکههای کریستالی تمامی بلورهایی که در جهان وجود دارند به هفت نوع تقسیمبندی میشوند. نامگذاری این هفت شبکه کریستالی بر اساس تقارن آنها صورت میگیرد و نام آنها به صورت زیر است:
- تریکلینیک (سه شیب)
- مونوکلینیک (یک شیب)
- ارتورمبیک (همه چیز قائم است)
- تتراگونال
- تریگونال یا رمبوهدرال
- هگزاگونال
- مکعبی
این هفت شبکه کریستالی در پارامترهای شبکه با هم تفاوت دارند، البته با این حال طبقهبندی این ۷ شبکه بر پایه متریک نیست بلکه براساس تقارن آنهاست که به نوبه خود باعث تغییر در پارامترهای شبکه نیز میشود. در جدول زیر هفت شبکه کریستالی با مشخصات متریک و نمادی که مشخص کننده بیشترین تقارن آنهاست به طور خلاصه فهرست شده است.
| سیستم کریستالی | طول محورها | زاویه بین محورها |
| تریکیلینیک | مقدار دلخواه | مقدار دلخواه |
| مونوکلینیک | مقدار دلخواه | |
| اروتورمبیک | مقدار دلخواه | |
| تتراگونال | a=b | |
| تریگونال | a=b | |
| هگزاگونال | a=b | |
| مکعبی | a=b=c |
در شبکه کریستالی تریکلینیک هیچ محدودیتی برای اندازه یالها و زاویههای میان آنها وجود ندارد. در شبکه کریستالی مونوکلینیک همچنین محدودیتی برای اندازه یالها وجود ندارد اما در مورد زاویهها میتوان گفت تا حدی این محدویت وجود ندارد زیرا دو زاویه برابر ۹۰ درجه هستند. بنابراین این دو زاویه مقدار مشخصی را دارند اما یک زوایه دیگر این محدویت را ندارد.
در واقع سیستم کریستالی مونوکلینیک توسط دو زاویه عمود برهم مشخصهیابی میشود یعنی این دو زاویه عمود برهم باعث تقارن در سلول واحد میشوند. توجه داشته باشید که زاویه سوم به طور تصادفی میتواند ۹۰ درجه باشد اما اینکه لزوما به این صورت باشد اینگونه نیست. تقارن در شبکه کریستالی ارتورمبیک به گونهای است که همه زاویهها در آن عمود بر هم هستند. در حالیکه یالهای این نوع شبکه کریستالی میتواند هر مقداری را داشته باشند.
سه شبکه بلوری بعدی یعنی تتراگونال، تریگونال و هگزاگونال به این صورت هستند که تقارن در آنها به نحوی است که طول یالها با هم برابر و زاویههای میان آنها مقدار مشخصی دارند. توجه داشته باشید که در سیستمهای تتراگونال همه زاویهها برابر ۹۰ درجه و و برای تریگونال و هگزاگونال دو زاویه برابر ۹۰ درجه و یک زاویه برابر ۱۲۰ درجه است. از بین این هفت شبکه بلوری، شبکهای که بیشترین تقارن را دارد شبکه مکعبی است که که تمامی زاویهها و طولها باهم برابر و مقدار مشخصی دارند. زاویهها همگی در این شبکه کریستالی برابر ۹۰ درجه هستند.
۱۴ شبکه براوه در کریستالوگرافی
یکی از مهمترین مفاهیم در کریستالوگرافی، شبکههای براوه است که تعداد آنها ۱۴ است. البته از این تعداد، در قسمتهای قبلی ۷ شبکه کریستالی معرفی شد. در واقع میتوان گفت که هر کدام از این دستگاههای کریستالی دارای زیردستگاه یا زیر شبکه هستند که در کنار هم ۱۴ شبکه براوه را تشکیل میدهند. دستگاههای کریستالی خود میتوانند به انواع زیر تقسیم شوند:
- ساده (Simple Cubic | SC)،
- مرکزپر (Body Centred Cubic | BCC)،
- قاعدهپر (Base Centred Cubic | BCC)
- وجهها پر (Face Centred Cubic | FCC)
لازم به ذکر است که ۷ دستگاه کریستالی که در قسمت بالا در مورد بررسی قرار گرفتند همگی از نوع شبکه بلوری ساده بودند و در هر یک از حالات فوق تعداد اتمها متفاوت است. در این قسمت نحوه آرایش اتمها و همچنین تعداد آنها را در هر یک از ۱۴ شبکه براوه بررسی میکنیم.
مکعبی
دستگاه کریستالی مکعبی در سه نوع ساده، مرکزپر و وجهپر میتواند باشد که هر کدام از این حالات در تصویر زیر نشان داده شده است. در حالت ساده تعداداتمها برابر یک ، در مکعبی مرکزپر برابر دو و در حالت وجهپر تعداد اتمها برابر ۴ است.
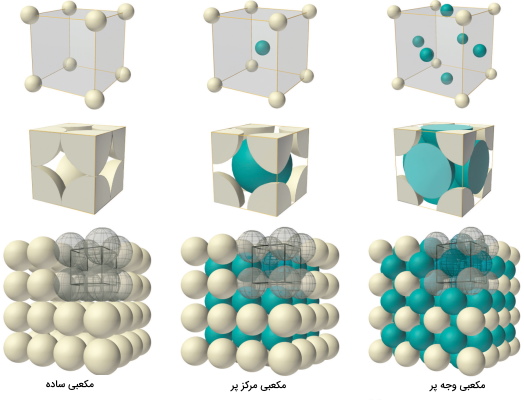
نحوه محاسبه تعداد اتمها به این صورت است که در هشتگوشههای مکعب، اتم وجود دارد اما فقط یکهشتم آنها در داخل مکعب قرار می گیرند (مکعبی ساده)، در حالت مرکزپر علاوه بر تعداد اتمها در مکعبی ساده یک اتم هم در مرکز وجود دارد. در حالت وجه پر علاوه بر حالت مکعبی ساده در وجهها هم اتم وجود دارد که تنها یک دوم از آنها در داخل مکعب قرار میگیرند. این نکته را به خاطر داشته باشید که در گوشههای مکعب یکهشتم اتمها و در وجههای مکعب یکدوم اتمها در داخل مکعب یا همان سلول واحد قرار میگیرند.
اورتورمبیک
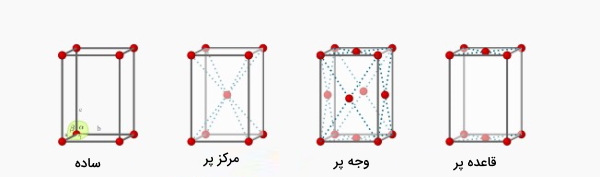
دستگاه کریستالی اروتورمبیک دارای ۴ حالت ساده، مرکزپر، قاعدهپر و وجهپر است که تصویر این چهار حالت در زیر آورده شده است. تعداد اتمها برای سه حالت مکعبی ساده، مرکز و وجه پر همانند مکعبی است. تعداد اتم هم در حالت قاعدهپر همانند مرکزپر برابر ۲ است اما قرارگیری اتمها با هم تفاوت دارند. بنابراین در حالت قاعدهپر نحوه محاسبه تعداد اتمها به صورت است.
تتراگونال
دستگاه کریستالی تتراگونال دارای دو حالت ساده و مرکزپر است که تعدا اتمها برای هر یک از این دو حالت در قسمتهای قبلی مشخص و محاسبه شده است.
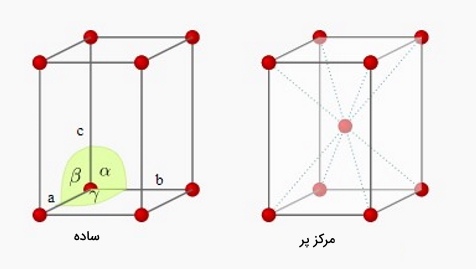
مونوکلینیک
دستگاه کریستالی تتراگونال دارای دو حالت ساده و قاعدهپر است که تعدا اتمها برای هر یک از آنها در قسمتهای قبلی مشخص شده است.
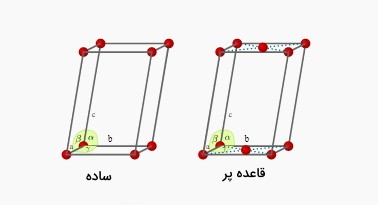
تریکلینیک و تریگونال
دستگاه کریستالی تریکلینیک و تریگونال تنها حالت ساده دارند که تعداد اتم در این حالت همانطور که در قسمتهای قبلی محاسبه شد برابر ۱ است.
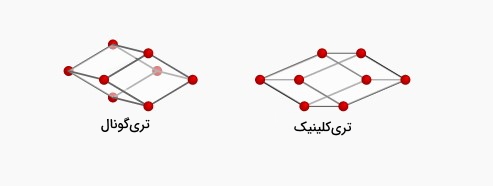
هگزاگونال
دستگاه کریستالی هگزاگونال همانند شکل زیر حالت فشرده (Hexagonal Close-Packed | HCP) دارد که نحوه آرایش اتمها در این سیستم کریستالی در زیر آورده شده است. همانطور که در تصویر مشاهده میشود تعداد اتم در این حالت برابر ۶ است.
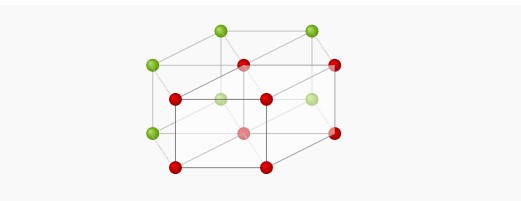
اگر همه حالات فوق را با هم جمع کنید به عدد ۱۴ خواهید رسید، به این ۱۴ شبکه یا دستگاه کریستالی ۱۴ شبکه براوه میگویند. به عبارتی در هر نقطه از فضای سه بعدی تنها ۱۴ شبکه کریستالی مستقل وجود دارد که این ۱۴ شبکه در ۷ دستگاه کریستالی تقسیمبندی میشوند.
اندیس میلر در کریستالوگرافی
اندیس میلر از سه عدد تشکیل شده که جهت صفحه یا صفحههای موازی اتمها در بلور را نشان میدهد. در واقع، خانواده صفحههای شبکه براوه توسط سه اندیس ، و که همان اندیسهای میلر هستند مشخص میشوند. این اندیسها اعداد صحیح را میتوانند اختیار کنند. آنها به صورت برای نمایش دادن صفحههای موازی ۱۴ شبکه براوه نمایش داده میشوند. البته علاوه بر صفحههای موازی، اندیسهای میلر برای نشان دادن بردار در سلولهای واحد نیز مورد استفاده قرار میگیرند که در این حالت بردارها به صورت [hkl] نشان داده میشوند. به مثالهای زیر دقت کنید:
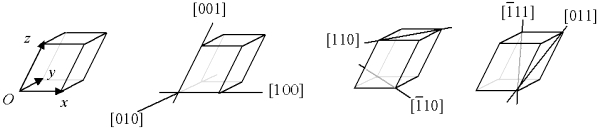
حال نمایش صفحات کریستالی را با اندیسهای میلر میبینیم.
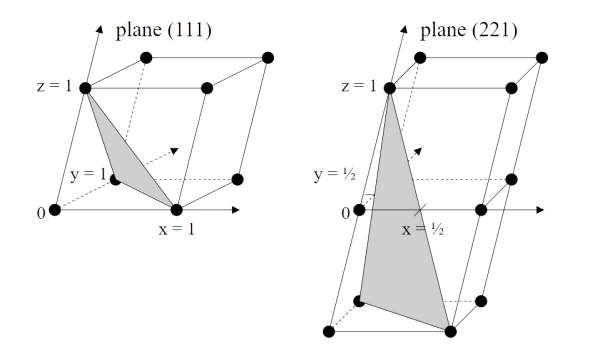
در ادامه برای نشان دادن بردارها و صفحات کریستالی با استفاده از اندیسهای میلر نکاتی وجود دارد که به آنها میپردازیم:
صفر تا صد نمایش اندیس میلر در بردار
برای رسم بردار با اندیسهای میلر :
- نقطهای را به عنوان مبدأ برای بردارها در نظر بگیرید. برای بردارهای ساده به راحت میتوان نقطهای را به عنوان مبدا انتخاب کرد. برای بردارهای پیچیدهتر این کار کمی سختتر خواهد بود. انتخاب مبدا با مختصات مهمترین بخش است زیرا اگر به درستی انتخاب نشود بردار به درستی اندیسگذاری نمیشود.
- با قلم خود به سمت هر جهت حرکت کنید، در سمت برای ، در سمت برای و در سمت برای پیش روید. اگر جهت بردارها منفی بود باید در سمت عکس مبدأ حرکت کنید. بعد از حرکت نقاط انتهایی را علامتگذاری کنید.
- بعد از علامتگذاری باید مطمئن شوید که بردار، نقاط انتهایی را قطع میکنند یا خیر. در صورتیکه قطع نکند اندیس میلر آن جهت صفر خواهد بود.
- در صورتیکه بردار یک یا همه جهتهای بردار مختصات را به گونهای قطع کرد که اعداد کسری بودند باید سه اندیس میلر را در کوچکترین مخرج مشترک ضرب کرد.
- در صورتی که یک یا همه جهتهای بردار منفی بودند باید در بالای اندیس میلر مربوط به آن جهت علامت منفی را در بالای آن (ها) قرار دهیم.
مثال
اندیس میلر بردارهای زیر را بنویسید.
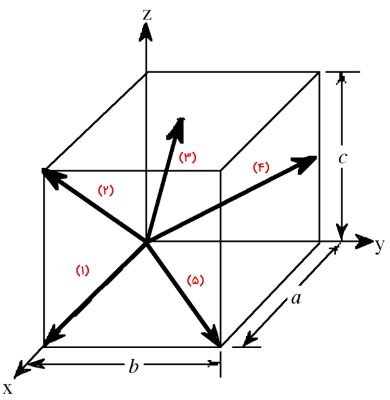
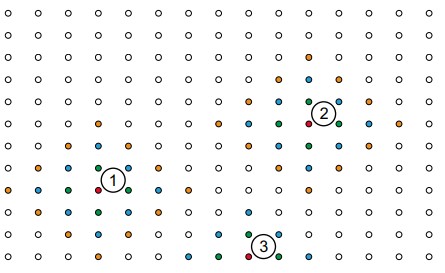
حل: در تصویر زیر محل تقاطع هر بردار نشان داده شده است اما برای درک و تصور بهتر برای هر بردار جداگانه به صورت تشریحی نیز پاسخ میدهیم:
- بردار شماره (۱): این بردار دقیقا بر روی جهت قرار گرفته بنابراین دو بردار و را قطع نمیکند. پس اندیس میلر آن به صورت خواهد بود.
- بردار شماره (۲): بردار شماره ۲ در وجه جانبی قرار گرفته که دو جهت و متعلق به آن است. بنابراین تنها دو بردار و را قطع میکند. در این صورت اندیس میلر آن به صورت نمایش داده میشود.
- بردار شماره (۳): این بردار از مرکز شروع میشود و به صورت مورب به مرکز وجه بالایی مکعب ختم میشود. در این حالت در جهت منفی بردار و در جهت مثبت بردارهای و را قطع میکند. در این حالت اندیس میلر برابر است با:
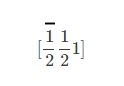
از آنجا که اندیس میلر نمیتواند عدد کسری باشد باید تمامی این ۳ اندیس میلر را در مخرج (۲) ضرب کرد. پس داریم:
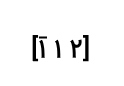
- بردار شماره (۴): این بردار از مبدا مختصات شروع و به وجه سمت راست مکعب منتهی میشود که تنها دو بردار و را قطع میکند. پس اندیس میلر آن برابر با است که در نهایت به صورت نمایش داده میشود.
- بردار شماره (۵): این بردار در وجه پایینی با دو جهت و قرار دارد بنابراین بردارهای این دو جهت یعنی و را قطع میکند. پس اندیس میلر آن به صورت نمایش داده میشود.
صفر تا صد نمایش اندیس میلر در صفحات بلوری
برای ترسیم اندیس میلر برای صفحات کریستالی در سلول واحد باید مرحله به مرحله به صورت زیر عمل کرد:
- بر روی جهتهای ، و بردارهای ، و را مشخص و همانند اندیس گذاری بردارها نقطه مشخصی را انتخاب کنید.
- در جهت بردارها حرکت کنید تا صفحات را قطع کند. در صورتیکه صفحهای را قطع نکرد اندیس بینهایت خواهد بود.
- در نهایت اندیس میلرها را بنویسید. توجه داشته باشید در این حالت نیز اندیس میلر به شکل کسری نمیتواند باشد. در صورتیکه اندیس کسری باشد باید آنرا در ابتدا معکوس کرد و اگر همچنان کسری بود در کوچکترین مخرج مشترک سه اندیس میلر آن را ضرب کرد.
مثال
اندیس میلر صفحات زیر را بنویسید.
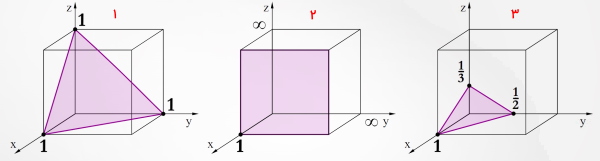
حل: در ابتدا مانند تصویر زیر مبدأ را انتخاب میکنید و هم جهت با بردارهای ، و حرکت کنید. صفحههای شماره ۱ و شماره ۳ تمامی سه جهت را در نقاط مختلف قطع میکنند اما در صفحه شماره ۲ تنها جهت را قطع میکند. این صفحه یکی از وجههای کناری کریستال است. بنابراین اندیس میلر برای این سه صفحه به صورت تصویر زیر خواهد بود.
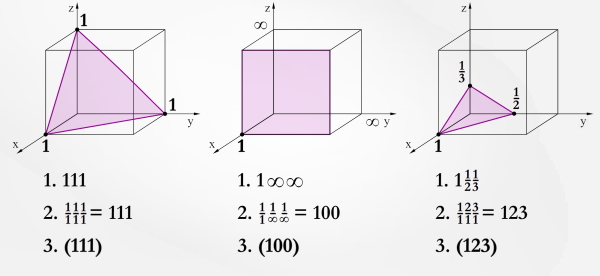
شبکه و موتیف
در کریستالوگرافی به موتیف پایه هم میگویند. در واقع موتیف به طور کامل توضیح میدهد هر شبکه کریستالی تنها شامل شبکه نیست و یک شبکه کریستالی از مجوعه شبکه و موتیف با هم تشکیل می شود. در ابتدا به تعریف واژه شبکه میپردازیم و در نهایت موتیف را توضیح میدهیم. شبکه یک ساختار هندسی است که میتواند به صورت زیر تعریف شود:
«شبکه از کنار هم قرار دادن بینهایت نقطه در فضای سهبعدی، صفحه (دوبعدی) یا یک خط (یکبعدی) تشکیل میشود که همه این نقاط آرایش یکسانی دارند و به ترتیب در کنار هم قرار می گیرند.»
شکل زیر قسمتی از یک شبکه دو بعدی را نشان میدهد. همانطور که مشخص است هر نقطه از شبکه دارای آرایشی یکسان است.

حال در تصویر زیر سه محل مشخص انتخاب شده است که هر محل با نقاط رنگی مشخص شده است. نقطه یک (قرمز) چند نقطه به عنوان همسایه دارد که با رنگهای آبی، نارنجی و سبز مشخص شدهاند. همین طرز چینش در نقطه شماره دو هم دیده میشود. نقطه سه که در خطوط مرزی وجود دارد آرایش متفاوتی را به نسبت نقطه یک و دو نشان میدهد. اگرچه در حقیقت، بلورهای واقعی به طور بینهایت بزرگ نیستند و مرزهای سطحی دارند.
سوال اساسی این است که شبکه کریستالی در واقع چه مفهومی را نشان میدهد؟پاسخ احتمالی به این سوال میتواند این باشد که شبکه کریستالی به عنوان یک نقطه اتصال بین سلولهای همسایه در نظر گرفته میشود. در تصویر شماره (۱) قسمتی از بلور به صورت سلولهای واحد به هم چسبیده نشان داده شده است. حال اگر یک نقطه از شبکه را در هر گوشه از سلول واحد قرار دهیم و مرزها را تغییر دهیم میتوانیم یک شبکه خالی را داشته باشیم که حالت دوبعدی آن در تصویر شماره (۲) نشان داده شده است.
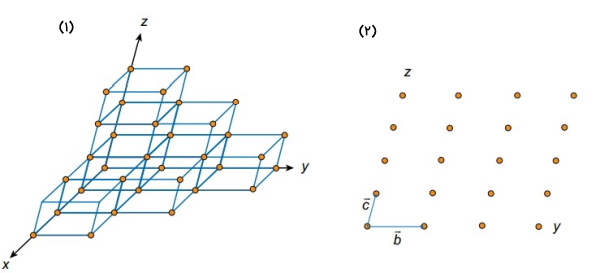
هر شبکه بر اساس بردارهای خود تعریف می شود. منظور از بردارهای شبکه میتواند نقاط شبکهای یا سه جهت ، و باشد. همچنین این مشخصه از شبکه کریستالی بر اساس ابعاد طولی و جهت تعریف میشوند. به عنوان مثال در شکل فوق مولفههای b و c در راستای جهتهای y و z هستند. در واقع میتوان گفت این سه مولفه مانند علائم راهنمایی رانندگی هستند، به این صورت که اگر شما در یک نقطه مشخص از شبکه ایستاده باشید، چه فاصلهای را در چه جهتی باید طی کنید تا به نقطه دیگری از شبکه برسید؟
تا الان با مفهوم شبکه کریستالی آشنا شدید و منظور آن را درک کردید پس به توضیح در مورد موتیف میپردازیم. در قسمتهای قبلی توضیح داده شد که کوچکترین بخش از ساختار ماده با یک شکل هندسی خاص تعریف میشود که این شکل هندسی در طول ساختار ماده تکرار می شود (سلول واحد). اما توجه داشته باشید که سلول واحد خالی نیست و آنها با موتیف یا پایه پر میشوند. به عنوان مثال شانه تخم مرغ را در نظر بگیرید هر خانهای که تخم مرغ در آن مینشیند یک سلول واحد فرض کنید، در این صورت تخممرغها که در آن قرار دارند همان موتیف هستند.

موتیف شامل ترتیب قرارگیری گونههای شیمیایی در بلور است. در بلورهای واقعی این گونههای شیمیایی اتمها یا مولکولها هستند. در حقیقت یک موتیف میتواند همه چیز باشد. هر نقطه از شبکه یک موتیف حقیقی را نشان میدهد. همیشه این موضوع را به خاطر داشته باشید که شبکه تنها یک مفهوم مجازی است که به کمک آن میتوان فاصله و جهتی که یک موتیف به موتیف دیگر وصل میشود را توصیف کرد. در واقع مجموعهای از شبکه، موتیف و سلول واحد با هم یک بلور را تشکیل میدهند.
آنیزوتروپی در کریستالوگرافی
همه بلورها یک ویژگی به نام آنیزوتروپی را از خود نشان می دهند. آنیزوتروپی در کریستالوگرافی به این معناست که برخی از خواص کریستالها یا همان بلورها به جهت آنها بستگی دارد. متضاد این کلمه برابر ایزوتروپی است و به این معناست که همه خواص در همه جهتها باهم برابر هستند. به عبارتی در این حالت این خواص مستقل از جهت هستند. برخی از خواص ماده مانند ضریب انبساط حرارتی، الاستیسیته، سختی و غیره مثالی برای آنیزوتروپی هستند.
به عنوان مثال برای خاصیت سختی در نظر بگیرید که بر روی قسمتی از بلور فشار وارد شود و در جهت دیگری از بلور، خبری از حضور این فشار نباشد. بنابراین سختی این بلور در همه نقاط یکسان نخواهد بود. مغناطش، پلاریزه الکتریکی، رسانایی حرارتی و الکتریکی نیز از این دسته مثالها هستند. گرافیت مادهای است که برای این این موضوع میتواند مثال بسیار خوبی باشد زیرا در گرافیت، رسانایی الکتریکی در امتداد جهت تک لایههای گرافن ۱۰۰۰۰ برابر بیشتر از مقدار رسانایی الکتریکی در جهت عمود بر این صفحات است. بنابراین زمانی که میخواهیم عدد رسانایی الکتریکی را برای گرافیت گزارش دهیم باید جهت آن را نیز ذکر کنیم زیرا این ویژگی برای همه جهتها یکسان نیست.
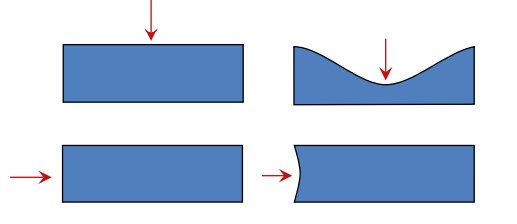
البته لازم به ذکر است که این خاصیت آنیزوتروپی صرفا مختص به مواد کریستالی نیست زیرا بسیاری از مواد غیرکریستالی هستند که برخی از ویژگیهای آنها آنیزوتروپ است. یک مثال آشنا برای این موضوع کاغذ است؛ با اینکه کاغذ ساختار کریستالی ندارد اما با اینحال خرد کردن آن اصولا در امتداد جهت الیافهای سلولوزی راحتتر از خرد کردن آن در جهت عمود بر الیافهای سلولوزی صورت میگیرد. در تصویر زیر مفهوم آنیزوتروپی نشان داده شده است. همانطور که در شکل مشخص است فشار در همه جهتهای ساختار وارد نمیشود.
فاکتور فشردگی اتمی چیست ؟
در کریستالوگرافی به کمک «فاکتور فشردگی اتمی« (Atomic Packing Factor | APF) میتوان دریافت که چند درصد از سلول واحد در کریستال از اتم تشکیل شده است. نحوه محاسبه فاکتور فشردگی اتمی برای هر یک از ۱۴ شبکه براوه برابر است با:
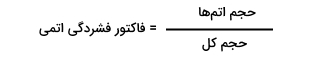
معمولا حجم تکرارشونده در ساختار کریستال، تنها حجم سلول واحد است که به عنوان حجم کل در نظر گرفته می شود. از طرفی با در نظر گرفتن اینکه اتمها اندازه برابری دارند و در شبکه کریستالی تکرار شونده قرار گرفتهاند میتوان رابطه فوق را به صورت زیر نوشت :
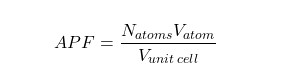
در رابطه فوق :
- : تعداد اتمها
- : حجم اتمها
- : حجم سلول واحد
از آنجا که شکل هر اتم به صورت کره در نظر گرفته میشود بنابراین حجم اتم مقدار مشخصی است پس در همه حالت رابطه روبرو برای حجم اتم برقرار است:
مثال فاکتور فشردگی اتمی در بلور شناسی
در این قسمت برای مهمترین شبکههای براوه یعنی مکعبی ساده، مکعبی مرکزپر، مکعبی وجهپر و هگزاگونال مثالهایی همراه با پاسخ آورده شده است تا بتوانید به درک بهتری از فاکتور فشردگی اتمی در کریستالوگرافی برسید.
مثال ۱
فاکتور فشردگی اتمی را برای شبکه کریستالی مکعبی ساده بدست بیاورید.
حل: طبق روابط فوق برای حل این سوال به تعداد اتم، حجم هر اتم و حجم سلول واحد نیاز داریم. برای مکعبی ساده همانطور که در قسمتهای قبلی اشاره کردیم یک اتم قرار دارد، حجم هر اتم که برابر با حجم کره و سلول واحد در اینجا مکعب است بنابراین حجم آن به صورت خواهد بود. در مکعبی ساده رابطه برقرار است.
بنابراین همه این مقادیر را در رابطه مربوط به فاکتور فشردگی اتمی قرار میدهیم یعنی:
مثال ۲
فاکتور فشردگی اتمی را برای شبکه کریستالی مکعبی مرکزپر بدست بیاورید.
حل: همانند مثال قبل همه موارد خواسته شده در فرمول را بدست آورده و در فرمول جایگذاری میکنیم. همانطور که گفتیم حجم اتم ثابت است و تغییری نمیکند زیرا همان کره است. اما تعداد اتم و پارامتر شبکه (a) متفاوت خواهد بود. تعداد اتم برای شبکه کریستالی مکعبی مرکزپر برابر با ۲ است و رابطه پارامتر شبکه بر حسب شعاع برابر است با: . حال این مقادیر را در رابطه مربوطه قرار میدهیم و فاکتور فشردگی اتمی را محاسبه میکنیم که این محاسبه به صورت زیر خواهد بود:
مثال ۳
فاکتور فشردگی اتمی را برای شبکه کریستالی مکعبی وجهپر بدست بیاورید.
حل: شبکه کریستالی مکعبی وجهپر دارای ۴ اتم است و پارامتر شبکه در این دستگاه کریستالی مانند شکل زیر برابر است با: . با جایگذاری این مقادیر در فرمول مربوط به فاکتور فشردگی اتمی خواهیم داشت:
مثال ۴
فاکتور فشردگی اتمی را برای شبکه کریستالی هگزاگونالی فشرده را بدست بیاورید.
حل: شبکه کریستالی hcp دارای ۶ اتم است و توجه کنید که در این قسمت حجم سلول واحد دیگر همانند مکعبی ساده به دست نمیآید. به طور کلی رابطه حجم برابر است با مساحت قاعده × ارتفاع. در این شبکه کریستالی، قاعده برابر ششضلعی است و مساحت آن به صورت رابطه زیر خواهد بود:
در رابطه فوق a همان پارامتر شبکه و c ارتفاع است که مقادیر آنها برحسب r طبق روابط زیر تعریف میشود:
حال با جایگذاری مقادیر فوق در رابطه مساحت، مساحت شبکه کریستالی هگزاگونالی فشرده برابر با خواهد بود. اکنون با جایگذاری تعداد اتم، حجم اتم و حجم سلول واحد در رابطه فاکتور فشردگی اتمی داریم:
در جدول زیر مقادیر مربوط به فشردگی اتمی در چهار شبکه کریستالی پر کاربرد و رایج در کریستالوگرافی فهرست شده است:
| ساختار کریستالی | فاکتور فشردگی اتمی |
| مکعبی ساده (SC) | ۵۲٪ |
| مکعبی مرکزپر (BCC) | ۶۸٪ |
| مکعبی وجهپر (FCC) | ۷۴٪ |
| هگزاگونال فشرده (HCP) | ۷۴٪ |
جمعبندی
در این مطلب سعی شد مفاهیم اولیه، ساده و در عین حال کاربردی در کریستالوگرافی بررسی شوند. این مفاهیم شامل سلول واحد، شبکه و موتیف، سیستمهای کریستالی و شبکههای براوه، آنیزوتروپی، تقارن و فاکتور فشردگی اتمی هستند. در این مطلب آموختیم که سلول واحد یعنی کوچکترین واحد در ساختار کریستالی که مانند یک الگو در کریستال البته با حفظ ساختار شیمیایی و خواص کل کریستال تکرار میشود. در واقع با کنار هم قرار گذاشتن این سلولهای واحد کل کریستال مجددا بهوجود میآید و یکی از ویژگیهای مهم سلول واحد تقارن آن است.
در شبکه بلوری بی نهایت نقطه در فضای خطی، صفحهای و فضایی میتواند قرار بگیرد به عبارتی در سلول واحد شبکه کریستالی توسط سه مولفه در راستای طول، عرض و ارتفاع تعریف می شود. فضای داخل این شبکهها اصولا خالی نیست و با اتم یا مولکول پر میشود و به این اجزایی که در شبکه قرار میگیرند موتیف یا پایه میگویند. در کریستالوگرافی ۱۴ شبکه براوه وجود دارد که این ۱۴ شبکه شامل ۷ سیستم یا دستگاه بلوری به همراه ساختارهای کریستالی مرکزپر، وجهها پر و قاعدهپر هستند. مجموع این ساختارهای کریستالی با هم ۱۴ شبکه براوه را تشکیل میدهند.
برخی از خواص مانند انبساط گرمایی در کریستالها یا سایر جامدات به جهت وابسته هستند که به این خواص، آنیزوتروپی میگویند. در نهایت فاکتور فشردگی اتمها نشان میدهد که چند درصد از سلول واحد دارای اتم است. طبیعتا هرچه این مقدار بیشتر باشد یعنی تعداد اتم بیشتری در سلول واحد وجود دارد بنابراین کریستال فشردهتر خواهد بود. با توجه به آنچه که در این مطلب توضیح داده شد ساختار کریستالی مکعبی وجهپر و هگزاگونال فشرده فاکتور فشردگی اتمی بالایی دارند یعنی کریستالهایی با این ساختار، ساختاری فشردهتر دارند.
سوالات متداول در رابطه با کریستالوگرافی
در این بخش از مطلب کریستالوگرافی، به سوالات متداول در رابطه با این موضوع پاسخ داده شده است تا کریستالوگرافی یا همان بلورشناسی را به خوبی یاد بگیرید.
بلورشناسی چیست ؟
کریستالوگرافی شاخهای از علم و مهندسی مواد است که با علم شیمی و فیزیک نیز رابطه مستقیمی دارد. زیرا برای بررسی خواص و ویژگیهای مواد از لحاظ فیزیکی و شیمیایی باید با ساختار ماده، نحوه قرارگیری اتمها یا مولکولها آشنایی داشت. علم کریستالوگرافی دقیقا به بررسی ساختار جامدات کریستالی یا بلوری میپردازد. از دید این علم به جامداتی «کریستال» گفته میشود که دارای نظم بلند دامنه هستند یعنی اتمها با یک آرایش خاصی در کنار هم قرار گرفتهاند.
به چه موادی، جامد بی شکل گفته میشود؟
جامدات بیشکل یا آمورف نقطه مقابل جامدات کریستالی هستند و به موادی گفته میشوند که اتمها با نظم خاصی قرار نگرفتهاند و طرز قرارگیری آنها به صورت تصادفی است. مثال بارز برای جامدات بیشکل میتواند شیشه باشد زیرا نحوه ساخت آن اینگونه است که مواد اولیه شیشه ابتدا تا دماهای بالا حرارت میبینند و به طور ناگهانی بدون فرصت دادن تا دماهای بسیار پایین سرد میشوند. به این صورت اتمها فرصت کافی را برای آرایش خاص و منظم پیدا نمیکنند و به صورت تصادفی در ساختار قرار میگیرند.
خواص آنیزوتروپی چه خواصی هستند ؟
برخی از خواص جامدات بلوری و حتی غیربلوری وابسته به جهت هستند یعنی با توجه به جهت تغییر میکنند. ازجمله این خواص میتوان به انبساط حرارتی، ضریب شکست، رسانایی، استحکام کششی و غیره اشاره کرد. گرافیت برای آنیزوتروپی مثال خوبی میتواند باشد زیرا رسانایی الکتریکی در تمامی جهات آن یکسان نیست.
چرا تنها ۱۴ شبکه براوه وجود دارد ؟
به دلیل اینکه تنها ۱۴ روش برای انتخاب بردارهای غیرمعادل در فضای سه بعدی وجود دارد به همین دلیل با استفاده ار این بردارها، ۱۴ شبکه فضایی متفاوت به نام شبکه های براوه به وجود میآید.
۷ سیستم بلوری در کریستالوگرافی کدامند ؟
در کریستالوگرافی ۷ سیستم یا دستگاه بلوری وجود دارد که این سیستمهای بلوری شامل مکعبی، تریکلینیک، مونوکلینیک، تتراگونال، اروترمبیک، رمبوهدرال و هگزاگونال هستند. هر کدام از این سیستمهای بلوری با توجه به نحوه قرارگیری در فضا دارای مشخصههای منحصر ب فردی هستند. به عنوان مثال در ساختار مکعبی ساده همه اضلاع با هم برابر و زاویه بین این ضلعها همگی باهم برابر با ۹۰ درجه هستند. به طور کلی از میان این ۷ سیستم بلوری، ساختار کریستالی مکعبی متقارنترین ساختار کریستالی است.












ساختار مرکز متقارن چیست؟
من مطالب را مطالعه کردم بسیار روان و کاربردی بوده است.
واقعا خسته نباشید
حتی با اجازه شما میلم این مطالب را در کتاب های تالیفی خودم با ذکر منبع اضافه کنم
با سلام؛
از بازخورد شما بسیار سپاسگزاریم. برای استفاده از مطالب مجله فرادرس میتونید به شرایط استفاده در انتهای صفحه یا این لینک مراجعه کنید.
با تشکر از همراهی شما با مجله فرادرس