قضیه تالس — به زبان ساده
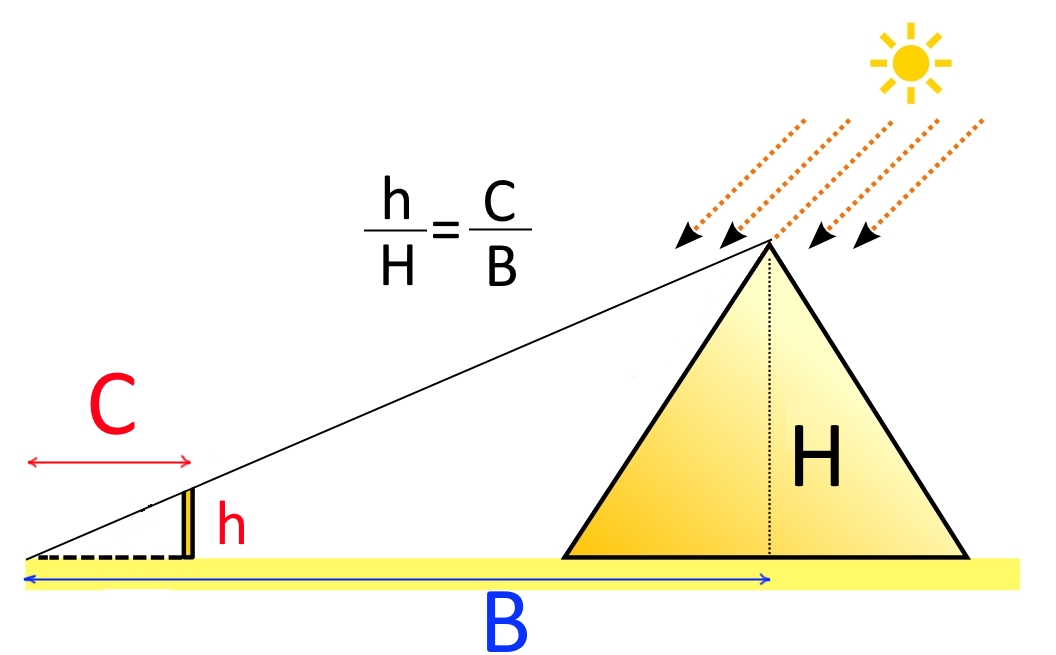
در این مطلب قصد داریم تا مفهومی را توضیح دهیم که حدود ۶۰۰ سال قبل از میلاد ارائه شده است. این مفهوم تحت عنوان قضیه تالس شناخته میشود. جهت درک این مفهوم در ابتدا لازم است تا با مفاهیم مربوط به نسبت دو طول آشنا باشید.
نسبتِ دو طول
جهت بیان قضیه تالس در ابتدا مطابق با شکل زیر دو پارهخط را در نظر بگیرید.
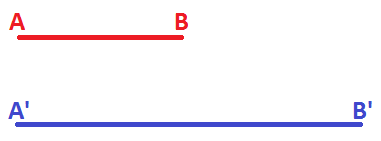
نسبت دو طول در شکل بالا برابر با حاصل تقسیم طول دو خط به یکدیگر است.
برای نمونه طول پارهخط AB برابر با ۵ سانتی متر و طول 'A'B برابر با ۱۰ سانتی متر است. در این صورت نسبت طول این دوخط برابر است با:
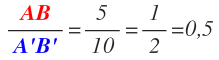
همانطور که در بالا محاسبه شد، نسبت طول این دو خط برابر با ۰.۵ است. در حقیقت طول AB نصف طول 'A'B است. البته رابطهی بین طولهای بالا را میتوان بهصورت عکس نیز بیان کرد.
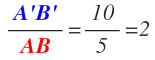
همانطور که رابطه بالا نشان میدهد، طول 'A'B دو برابر طول AB است. بنابراین دو جمله زیر معادل هم هستند.
- طول AB نصف طول 'A'B است.
- طول $$A'B'$$، ۲ برابر طول AB است.
بنابراین بهمنظور مقایسه طول دو پارهخط، تنها محاسبه یکی از نسبتهای بالا کافی است.
ارتباط بین دو نسبت
حال در این قسمت دو طولِ CD و 'C'D را نیز در نظر بگیرید. در زیر این دو طول، نشان داده شدهاند.
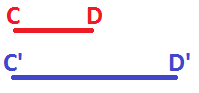
فرض کنید در شکل بالا طول CD برابر با ۳ سانتی متر و طول 'C'D برابر با ۶ سانتی متر است.
با این فرضیات با تقسیم طول CD به 'C'D داریم:
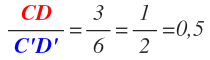
عدد بدست آمده در بالا نشان میدهد در این حالت نیز طول CD نصف طول 'C'D است. در حقیقت نسبت این دو با نسبت AB و 'A'B برابر است.

بنابراین نسبت طولها در شکل بالا برابر هستند.
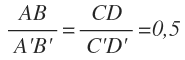
قضیه تالس
با توجه به توضیح بالا، زمان آن فرا رسیده که قضیه تالس را توضیح دهیم.
در ابتدا دو خط راستِ r و s را مطابق با شکل زیر در نظر بگیرید.
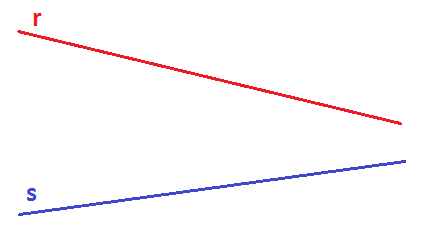
حال مطابق با شکل زیر دو خط بالا با خطوطی عمودی تقسیمبندی میشوند.
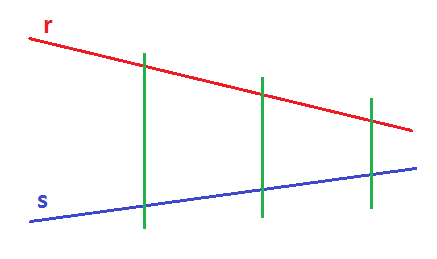
در مرحلهی بعد نقاط ایجاد شده روی خط قرمز رنگ، A,B,C و نقاط روی خط بنفش، 'A',B',C نامیده میشوند.
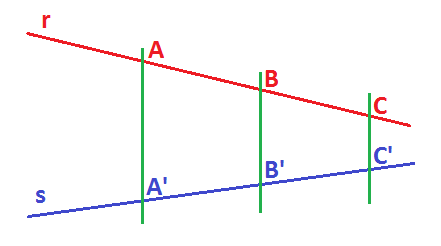
همانگونه که در شکل بالا مشاهده میفرمایید، خط قرمز رنگ به دو بخشِ AB و BC تقسیمبندی شده است. با دقتی بیشتر خواهید دید که پارهخط AC نیز در شکل بالا وجود دارد. بنابراین نهایتا سه پارهخطِ AB,BC,AC روی خط قرمز رنگ ایجاد شده است.
همانند خط قرمز رنگ، روی خط بنفش رنگ نیز ۴ پارهخطِ $$A'B',B'C',A'C'$$ ایجاد شده است. قضیه تالس بیان میکند که:
هرگاه چند خط موازی با استفاده از دو خط مورب، قطع شوند، نسبتهای ایجاد شده روی آنها با هم برابرند.
جمله بالا به چه معنا است؟ جهت درک بهتر، این قضیه را با استفاده از خطوط قرمز و بنفشِ ارائه شده در بالا توضیح میدهیم. همانطور که میبینید این دو خط، راست هستند. از طرفی خطوطِ سبز رنگ موازی یکدیگراند. بنابراین رابطه زیر بین طول پارهخطهای ایجاد شده برقرار است.
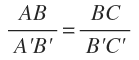
در حقیقت حاصل تقسیم هر طولی از خط بالا به هر طولی از خط پایین که بین خطوط سبز رنگ قرار گرفته، برابر با عدد ثابتی است. منظور ما از این جمله رابطه زیر است:
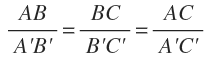
اثبات قضیه تالس
مثلث زیر را در نظر بگیرید. در شکل زیر میدانیم DE موازی AB است و میخواهیم تساوی $$\frac {AC}{CD}=\frac{BC}{CE}$$ را اثبات کنیم.
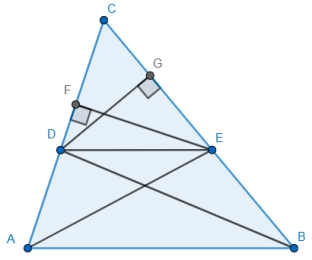
به دلیل یکی بودن ارتفاعها، تساوی $$\large{\frac{A_{\triangle{ACE}}}{A_{\triangle{CDE}}}=\frac{AC}{CD}}$$ را داریم. $$A$$ نماد مساحت است. به طور مشابه، میتوان نوشت: $$\large{\frac{A_{\triangle{BCD}}}{A_{\triangle{CDE}}}=\frac{BC}{CE}}$$.
مساحت مثلثهای ADE و BDE نیز برابر است، یعنی $$A_{\triangle{ADE}}=A_{\triangle{BDE}}$$. زیرا مساحت دو مثلث با ارتفاع برابر بین دو پارهخط برابر است. در نتیجه، $$A_{\triangle{ACE}}=A_{\triangle{BCD}}$$ و $$\frac{A_{\triangle{ACE}}}{A_{\triangle{CDE}}}=\frac{A_{\triangle{BCD}}}{A_{\triangle{CDE}}}$$. بنابراین، میتوان نتیجه گرفت:
$$ \large \frac{AC}{CD}=\frac{BC}{CE}$$
و اثبات کامل میشود.
پیشنهاد میکنیم جهت درکِ کامل قضیه تالس، مثالهای زیر را نیز مطالعه فرمایید.
مثال ۱
خطوط a,b در شکل زیر موازی یکدیگر هستند. خطی بهنام c را از خطوط سبز و آبی رنگ عبور میدهیم. طولهای ایجاد شده، روی شکل نشان داده شده است. به نظر شما آیا خط c با a,b موازی است؟
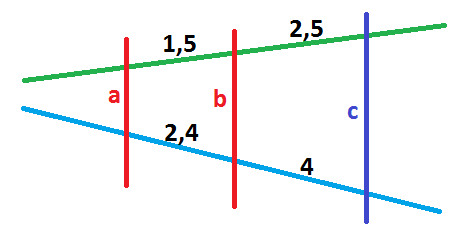
اگر خط c موازی دو خط دیگر باشد، نسبتهای ایجاد شده بایستی با یکدیگر برابر باشند. نسبت طولهای ایجاد شده بین a,b برابر است با:
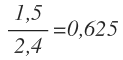
از طرفی نسبت طولهای بین خطوط b,c نیز برابرند با:
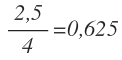
همانگونه که میبینید نسبت دو طول بدست آمده با هم برابر است؛ بنابراین خط c با خطوط a,b موازی است.
مثال ۲
اندازه طول x در شکل زیر چقدر است؟
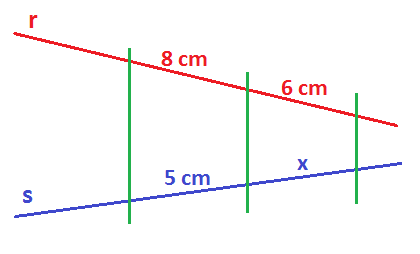
در شکل بالا دو خطِ راستِ قرمز و بنفش، با سه خطِ موازی سبز رنگ قطع شدهاند. در نتیجه قضیه تالس برای این مسئله صادق خواهد بود. نسبت طولهای سمت چپ و راست برابر هستند با:
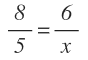
با استفاده از ضرب متقاطع داریم:
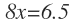
نهایتا مقدار x برابر است با:
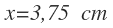
قضیه تالس در بالا بیان شد. البته از این قانون نتایجی نیز بدست میآید که خصوصا در بدست آوردن اضلاع مثلث کاربرد بسیاری دارد. برای مثال مطابق با شکل زیر مثلثی با رئوس ABC را در نظر بگیرید. فرض کنید خطی موازی BC، مثلث را به دو قسمت تبدیل میکند.
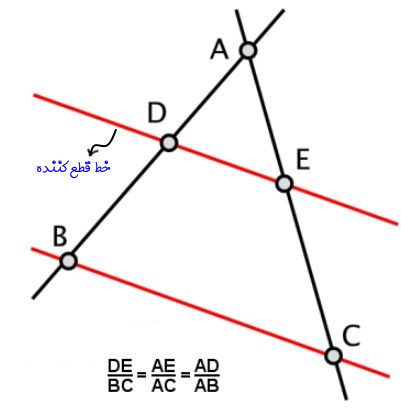
در شکل فوق روابط زیر برقرار خواهند بود. این رابطه در نتیجه قضیهی تالس بدست میآید.
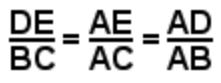
شاید عجیب باشد ولی با استفاده از رابطه فوق میتوانید طول یک برج بلند را با استفاده از طول سایه آن بدست آورید. در مثال ۳ چنین کاری انجام شده است.
مثال ۳
فرض کنید میخواهیم ارتفاع اهرام ثلاثه مصر را بدست آوریم. در این حال شخصی که قدش برابر با ۱.۸ متر است، در فاصلهای از برج میایستد، به نحوی که نوک سایهی اهرام و سایهی شخص در یک نقطه قرار میگیرند (شکل زیر).

با فرض اینکه طول سایه شخص برابر با ۹ متر و طول سایه اهرام برابر با ۶۹۵ متر باشد، ارتفاع اهرام چند متر خواهد بود؟
با توجه به اینکه نوک سایه اهرام و شخص در یک نقطه قرار دارند، بنابراین شعاع نور عبوری روی اهرام و شخص، وتر مثلثی قائم الزاویه مطابق با شکل زیر است.
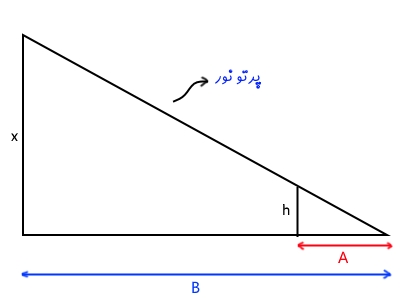
قضیه تالس برای مثلث بالا را میتوان در قالب رابطهی زیر بیان کرد:
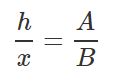
با جایگذاری مقادیر در رابطهی بالا داریم:
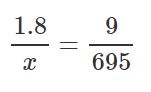
با استفاده از ضرب متقاطع، مقدار x برابر با عدد زیر بدست میآید.
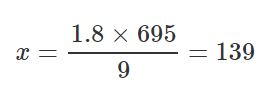
بنابراین ارتفاع اهرام ثلاثه با استفاده از قضیه تالس برابر با ۱۳۹ متر بدست آمد. قضیهی تالس مفهومی پرکاربرد در ریاضیات و علوم تجربی محسوب میشود. این قضیه حتی در مباحث اپتیک در فیزیک نیز کاربرد دارد.
در صورت علاقهمندی به مباحث مرتبط در زمینهی ریاضیات و فیزیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای ریاضیات
- مجموعه آموزشهای ریاضی و فیزیک
- مجموعه آموزشهای دبیرستان و پیشدانشگاهی
- آموزش جامع هندسه دبیرستان
- سینوس، کسینوس و تانژانت یک زاویه — به زبان ساده
- قانون سینوسها (Law of Sines) — به زبان ساده
^^











اقا این توضیح فوق العاده بود
مرسی واقعا
ممنون از توضیحتون. فقط توی خط اول اثبات، نوشتید که DE موازیه با BC، در حالی که DE با BA موازیه.
سلام.
متن تصحیح شد.
سپاس از همراهی و بازخوردتان.
سلام خسته نباشید . ممنون از مطالبت خوبتون فقط ببخشید شما این مسئله رو اثبات نکردید اگر میشه این قضیه رو هم اثبات کنید بسیار بهتر میشه ممنون از شما 🙂
سلام.
اثبات قضیه تالس به متن اضافه شد.
سپاس از همراهی و بازخوردتان.
سلام ، خسته نباشید سایتتون عالیه ، هر مبحث ریاضی سایتتون خیلی کامله و عالیه و هم اینکه بصورت ویدیویی توضیح دادین عالی ترش میکنه
سلام
لطفا اثبات قضیه تالس را هم اضافه کنید.
با تشکر
عالی بود فقط اونجا که نوشتید 4 پاره خط باید مینوشتید 3 پاره خط اشتباه تایپی دارد
سلام.
اشتباه تایپی مورد نظر اصلاح شد.
از توجه شما سپاسگزاریم.