شدت صوت — به زبان ساده

یکی از مهمترین موجهایی که روزانه استفاده زیادی از آن داریم، موج صوتی است. گفتگو، شنیدن موسیقی، بوق زدن و ... همه از امواج صوتی حاصل میشوند. همانطور که میدانید امواج صوتی در دسته امواج مکانیکی جای میگیرند، چرا که برای انتشار به محیط مادی نیاز دارند. در این مقاله قصد داریم تا با زبانی ساده با مقوله شدت صوت آشنا شویم. آیا تا به حال به لرزش ایجاد شده در شیشه، بدنه ماشین، وسایل خانه به هنگام پخش موسیقی با صدای بلند دقت کردهاید؟ قاعدتاً لرزش ایجاد شده به واسطه انتقال انرژی صورت میگیرد. به طور ساده میتوان شدت صوتی را که به یک صفحه میرسد، آهنگ متوسط انتقال انرژی (توان) بر واحد آن سطح تعریف کرد.
در رابطه فوق، توان موج صوتی و مساحت صفحهای است که موج صوتی به آن برخورد میکند. در ادامه این مقاله، پس از معرفی صوت و چگونگی تشکیل آن، با مقیاس «دسیبل» (Decibel) و تراز صدا آشنا میشویم. با ما در ادامه این مقاله همراه باشید.
موج صوتی
قبل از این که به بحث شدت و تراز صوتی بپردازیم، بهتر است که نگاهی مختصر به فیزیک موج صوتی داشته باشیم. برای اینکه درک شهودی بهتری از چگونگی تشکیل امواج صوتی داشته باشیم، در زیر فرآیند تولید صوت به وسیله ابزاری به نام دیاپازون را شرح میدهیم.

لازم به ذکر است که دیاپازون ساختاری دوشاخه و ساده مطابق با شکل (۱) دارد. اگر به یکی از شاخههای آن ضربهای وارد کنیم، هر دو شاخه با حرکت هماهنگ ساده شروع به نوسان میکنند. توجه شود که این نوسان «میرا» (Damp) است، یعنی اینکه دامنه موج در حین نوسان کم شده و در نهایت به صفر میرسد (شکل 2). در واقع پس از گذشت مدت زمانی مشخص، نوسان دوشاخههای دیاپازون میرا شده و باز میایستند.
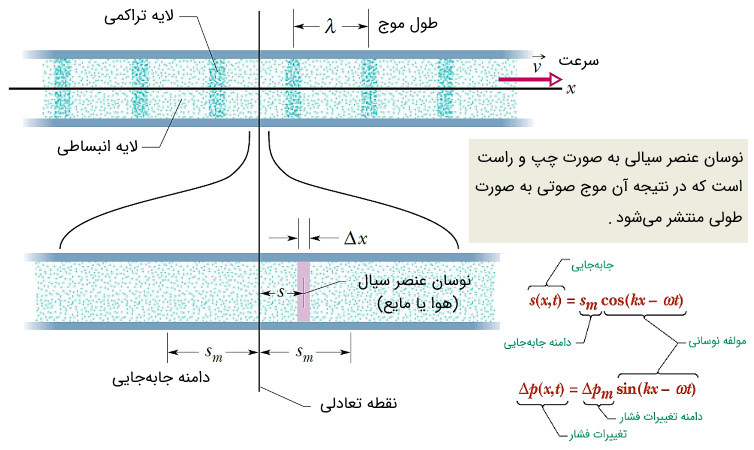
حال مطابق با شکل (3) یک دیاپازون را در نظر بگیرید که در حال تعادل است. به هنگام تعادل دیاپازون، چگالی و فشار هوای اطراف آن در همه جا ثابت بوده و به ترتیب برابر مقدار و است. به هنگام نوسان، هنگامی که شاخههای دیاپازون به یکدیگر نزدیک شوند، هوای بین آنها فشرده شده و در نتیجه چگالی و فشار در بین شاخهها نسبت به حالت قبل (تعادل) بیشتر میشود. در واقع یک لایه متراکم با نزدیک شدن شاخههای دیاپازون به یکدیگر تشکیل شده که این لایه متراکم (هوای متراکم شده بین دو شاخه را یک لایه در نظر بگیرید) نیز میتواند لایه مجاور خود را متراکم کند. بدین ترتیب یک آشفتگی یا تپ تراکمی (پرفشار) در هوا ایجاد شده و به طور طولی منتشر میشود. توجه داشته باشید که امواج صوتی، امواجی طولی هستند، چرا که ذرههای هوا در راستای انتشار نوسان میکنند.
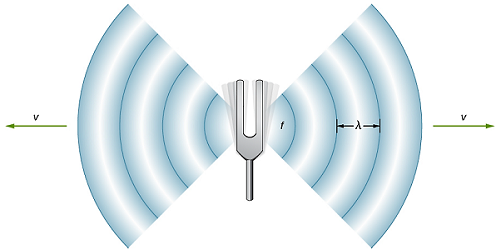
در حالت عکس، یعنی زمانی که شاخههای دیاپازون از یک دیگر دور میشوند، چگالی و فشار هوای بین دو شاخه نسبت به حالت تعادل کاهش پیدا میکند. این لایه انبساط یافته، به صورت یک تپ انبساطی (کم فشار) در هوا به صورت طولی منتشر می شود. با این تفاسیر به هنگام نوسان شاخههای دیاپازون، تپهای متوالی تراکمی و انبساطی در هوا به صورت طولی مطابق با شکل (4) منتشر میشوند.
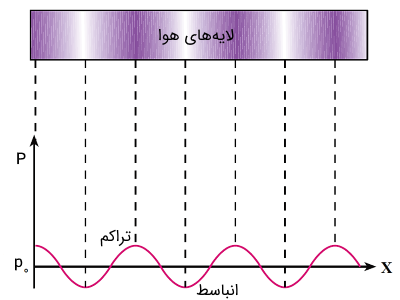
دقت داشته باشید که به هنگام انتشار امواج مکانیکی در محیط، ذرات محیط منتقل نمیشوند، بلکه تنها حول نقطه تعادلی خود نوسان میکنند. در انتشار امواج صوتی، لایههای پرفشار (تراکمی) و کمفشار (انبساطی) در اثر نوسان ذرات هوا حول نقطه تعادل خود ایجاد میشوند و تنها تغییرات فشار یا چگالی هوا است که به صورت تپهایی متوالی به صورت طولی منتشر شده (به جلو میروند) و در نهایت میرا میشوند.
هر جسم مرتعشی در هوا را میتوان یک چشمه تولید امواج صوتی در نظر گرفت. یک چشمه صوتی میتواند به سادگی تکان دادن سریع یک بادبزن یا دیاپازون و یا همانند حنجره انسان پیچیده باشد.
شدت صوت
همانطور که در مقدمه اشاره کردیم، مقدار انرژی که در واحد زمان توسط موج صوتی حمل و به واحد سطح وارد میشود، شدت موج صوتی تعریف میشود. میدانیم که انرژی در واحد زمان، تعریف توان بوده که واحد آن «وات» (Watt) است، پس در سیستم بینالمللی SI واحد شدت، وات بر متر مربع () است که از رابطه () نیز این امر مشخص است.
شدت صوت به مربع دامنه تغییرات فشار، طبق رابطه زیر ارتباط پیدا میکند:
در رابطه فوق، تغییر فشار یا دامنه فشار (نصف اختلاف بین ماکزیمم و مینیمم فشار در موج صوتی) است که واحد آن پاسکال () یا نیوتن بر مترمربع () است. دقت کنید که در اینجا نماد برای فشار را با نماد برای توان به اشتباه نگیرید. انرژی جنبشی یک جز نوسانی هوا که در اثر عبور صوت به نوسان در میآید، متناسب با مربع دامنه است. همچنین پارامتر با واحد کیلوگرم بر متر مکعب ()، چگالی محیطی است که موج صوتی در آن منتشر میشود. با واحد متر بر ثانیه () نیز سرعت حرکت موج صوتی است. تغییرات فشار نیز متناسب با دامنه نوسان موج است که در نتیجه آن شدت صوت متناسب با مربع تغییرات فشار میشود. به شکل (۶) دقت کنید.
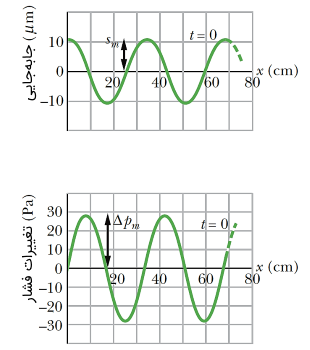
ثابت میشود که تغییرات فشار به سرعت انتشار، فرکانس موج، چگالی محیط و جابهجایی به صورت زیر رابطه دارد که در نتیجه آن، رابطه شدت صوتی به صورت زیر در میآید:
تغییر شدت با فاصله
ارائه رابطهای ساده برای تغییر شدت صدا بر حسب فاصله برای یک بلندگو که موج صوتی را در راستای خاصی منتشر میکند کار سادهتری است. اما در واقعیت به دلیل انعکاسهای محیط، موجهای بازتابیده روی موج صوتی اصلی میافتند یا با آن تداخل میکنند که در نتیجه نمیتوان رابطهای دقیق برای شدت موج اصلی ارائه کرد. با صرفنظر از طنینهای ایجاد شده در اثر بازتاب از محیط میتوانیم رابطهای ساده برای سنجش شدت صوت از یک منبع نقطهای صوتی ارئه کنیم.
اگر چشمه تولید موج صوتی، امواج را به طور یکنواخت در تمامی جهات منتشر کند، صوت به صورت امواجی کروی در فضا منتشر میشوند. چنین منبعی را منبع نقطهای تولید صوت مینامیم. حال اگر فرض کنیم که این منبع نقطهای صوت، امواج صوتی را به صورت یکسانگرد (شدت یکسان در تمامی جهات) منتشر کند، میتوان جبهههای موج را همانند شکل (۷) در نظر گرفت.
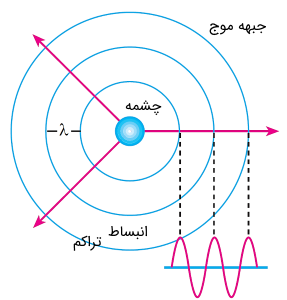
خیلی ساده با در نظر گرفتن کرهای فرضی به شعاع از منبع نقطهای، میتوانیم کل انرژیی که منبع صوتی تولید کرده و از سطح این کره گذر میکند را حساب کنیم. پس مطابق با رابطه () شدتی از صوت که ما در اطراف یک منبع نقطهای احساس میکنیم، با مربع فاصله از منبع، نسبت عکس دارد. یعنی:
حدود شنوایی انسان
ساختار گوش انسان توانایی تشخیص و شنیدن هر موج صوتی را ندارد. ساختار گوش انسان تنها میتواند امواج صوتی با فرکانس 20 هرتز تا 20.000 هرتز را تشخیص دهد و بشنوند. امواج صوتی که فرکانسی پایینتر از 20 هرتز دارند، «فروصوت» (Infrasound) و امواجی صوتی که فرکانس بالاتری از 20.000 هرتز دارند را «فراصوت» (Ultrasound) مینامند. در مقام مقایسه خفاشها میتوانند امواج صوتی تا فرکانس 100.000 هرتز را تشخیص دهند. همچنین سگها فرکانسهای بین 15 تا 50.000 هرتز را میتوانند بشنوند.
امواج فراصوت، به دلیل طول موج کوتاهشان کاربردهای فراوانی در علم پزشکی دارند. در واقع از بازتاب آنها میتوان بافتهای ریز درون بدن انسان را بررسی کرد. یکی از مهمترین کاربردهای امواج فراصوت، تصویر برداری از جنین است.
بلندی صدا در واقع همان شدت صدا است. آهستهترین (کم شدتترین) صدایی که گوش انسان قادر به تشخیص آن است را آستانه شنوایی مینامند. همچنین بلندترین صدایی (پر شدتترین) که آسیبی به گوش انسان وارد نمیکند و انسان قادر به تشخیص آن است، آستانه دردناکی نام دارد. نمودار شدت صوت بر حسب فرکانسهای قابل تشخیص برای انسان در شکل زیر آورده شده است.
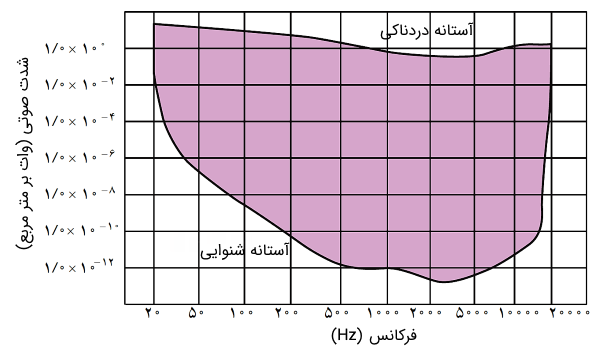
توجه شود ممکن است صدایی با فرکانس فراصوت که انسان توانایی شنیدن آن را ندارد، با شدت خیلی زیادی منتشر و به گوش انسان آسیب وارد کند. درست است که ما قادر به شنیدن آن نیستیم، اما به هر حال موجی است که توان خیلی زیاد را بر مساحت پرده گوش ما وارد میکند. اصولاً صداهای بم فرکانسی پایین و طول موج بالا و صداهای زیر، فرکانس بالا و طول موج پایینی دارند. از این حیث در سیستمهای صوتی، بلندگوهایی متفاوتی برای پوشش همه فرکانسهای صوتی به کار میبرند. بلندگوهای بزرگ برای تولید صوت با طول موج بالا به «ووفر» (woofer) و بلندگوهای کوچک برای تولید طول موجهای کوتاه، به «توئیتر» (tweeter) موسوم هستند.

مقیاس دسیبل
از نمودار شکل (9) مشخص است که نسبت شدت صدا برای محدوده شنوایی انسان (دو آستانه)، در واقع نسبت پرشدتترین به کمشدتترین صدا عددی در مرتبه است. برای راحتی کار با مقادیری که بدین صورت در گستره وسیعی تغییر میکنند، میتوانیم از نمایش لگاریتمی در پایه ۱۰ استفاده کنیم. برای اینکه بهتر متوجه موضوع شوید، تابع زیر را در نظر بگیرید:
در رابطه فوق، اگر را ۱۰ برابر کنیم، تنها یک مقدار افزایش پیدا میکند، یعنی:
پس با نمایش لگاریتمی، اگر (شدت صوت) را برابر کنیم، تنها ۱۲ واحد افزایش پیدا میکند. به همین دلیل بهتر است به جای شدت صدا که در رنج وسیعی تغییر میکند، از مفهوم جدید به اسم «تراز صوت» (Sound Level) استفاده کنیم. تراز صدا یا تراز شدت صوت به صورت زیر تعریف میشود که در آن ، شدت صوت مبنا است.
در رابطه فوق، مخفف «دسیبل» (Decibel) بوده که به افتخار «الکساندر گراهام بل» (Alexander Graham Bell) انتخاب شده است. شدت صوت مبنا () برابر با آستانه شنوایی انسان (گوش سالم) در فرکانس در نظر گرفته میشود. به ازای مقدار صفر شده که بدین معنی است، تراز مرجع استاندارد با مقدار 0 دسیبل متناظر شده است. در جدول زیر شدت صوت و تراز صدا برای چند صدای مختلف آورده شده است.
| نوع صدا | شدت صوت () | تراز شدت صوت () |
| شدت صوت مبنا (آستانه شنوایی) | 0 | |
| نفس کشیدن | 10 | |
| صدای برگ درختان در بادی ملایم | 20 | |
| گفتگو در فاصله یک متری | 40 | |
| همهمه و شلوغی یک فروشگاه | 60 | |
| خیابان شلوغ | 70 | |
| آستانه دردناکی در فرکانس | 120 | |
| اسلحه (مسلسل) | 130 | |
| موتور جت حین بلند شدن | 140 | |
| موشک فضایی موقع پرتاب | 170 |
در صورتی که مطلب فوق برایتان مفید بود، مطالب زیر به شما پیشنهاد میشود:
- مجموعه آموزشهای فیزیک
- آموزش آکوستیک (صوت شناسی – Acoustics)
- مجموعه آموزشهای مهندسی مکانیک
- سرعت صوت — از صفر تا صد
- عدد ماخ — به زبان ساده
- اثر دوپلر (Doppler Effect) — به زبان ساده
^^













خیلی خوب نوشته بودین مرسیی
با سلام مطالب مربوطه در حد رونوشت از کتاب فیزیک دبیرستان بخش امواج هست یهکاش یه مقدار تخصصی تر توضیح میدادین
سلام
آیا میتوان شدت صوت را گرفت و بتوان دستگاهی طراحی کرد که کلا صدا را گرفت
این درست است که اگر به آستانه شنوایی نزدیک شوی یعنی هرچه صدای آهسته ترب بشنویی شنوایی آن بهتر می شود ؟
سلام بله در عالی قاپو اصفهان 400 سال پیش انجام شده
من یه سوال دارم، ما اگه تعداد چشمه صوتی رو دو برابر کنیم، یعنی شدت صوت دو برابر میشه؟ برای مثال شدت صوت یک مسلسل 10 وات بر مترمربع هستش، اگه بیایم دو تا مسلسل قرار بدیم شدت صوتی دپ برابر میشه؟ و در این صورت اختلاف تراز شدت صوت فقط 30 دسی بل افزایش پیدا میکنه؟ منطقی نیست
افزایش تعداد چشمه های صوت مثل سایر روابط لگاریتمیه و بصورت زیر محاسبه می شود.
Log n * 10 = افرایش شدت صوت
که در آن n تعداد چشمه های صوتی است. مثلا ۲ تا بلند گو ۱0Log 2 یعنی 3db افزایش صوت ایجاد میکنه. برای دوتا مسلسل همین ۳db به شدت صوت یکی اضافه میشه
برای بلندگوی 10 واتی میشه 10log 10/10 (-12) که میشه 130db ,gd ,rjd ولی وقتی از دو بلندگو استفاده بشه میشه 10log20/10(-12) که جوابش میشه 133db
به نظر رابطه شدت امواج صوتی حاصل از ادغام دو منبع صوتی خیلی پیچیده تر از جمع جبری شدت اونها باشه