ارتعاشات آزاد با میراگر ویسکوز – به زبان ساده

پیش از این در مجله فرادرس، جنبه‌های مختلف ارتعاشات مکانیکی را مرور کردیم و در مقاله‌ای به بررسی دقیق ارتعاشات آزاد در سیستم‌های نامیرا پرداختیم. در این مقاله قصد داریم نگاهی به ارتعاشات آزاد در سیستم‌های میرا بیاندازیم و در اولین گام، میراگر ویسکوز (Viscous Damper) را مورد بررسی قرار خواهیم داد.

معادله حرکت در ارتعاشات آزاد با میراگر ویسکوز

همان‌طور که می‌دانید، نیروی میراگر ویسکوز (لزجی) $$\large F$$ با سرعت $$\large \dot{x}$$ یا $$\large v$$ متناسب است و می‌توانیم آن را به صورت زیر تعریف کنیم.

$$\large F\: =\:- c\dot{x}$$

در رابطه بالا، $$\large c$$ ثابت میرایی یا ضریب میراگر ویسکوز نام دارد و علامت منفی نیز نشان دهنده این است که نیروی میرایی در خلاف جهت سرعت وارد می‌شود. سیستم یک درجه آزادی با میراگر ویسکوز نشان داده شده در شکل زیر را در نظر بگیرید. اگر $$\large x$$ نسبت به موقعیت تعادل جرم $$\large m$$ اندازه گرفته شود، استفاده از قانون دوم نیوتن، معادله حرکت زیر را نتیجه می‌دهد.

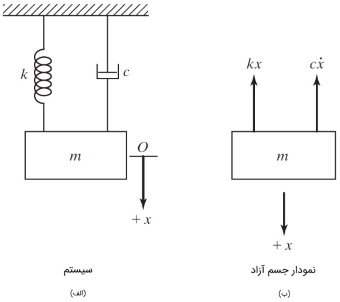
$$\large m\ddot{x} \:= \:-c \dot{x} \:-\: kx$$

(رابطه ۱)

برای حل معادله دیفرانسیل بالا، پاسخ را به صورت $$\large x(t) \:= \:C e^{st}$$ فرض می‌کنیم. در اینجا، $$\large C$$ و $$\large s$$ ثابت‌های نامعین هستند. با جایگذاری این تابع در رابطه ۱، معادله مشخصه زیر به دست می‌آید.

$$\large ms^2 \:+\: cs \:+\: k\:= \:0$$

ریشه‌های این معادله به صورت زیر است.

$$\large s_{1,2} \:=\: \frac {-c \:\pm \:\sqrt{ c^2 \:-\: 4mk}} {2m} \:=\: -\:\frac {c} {2m} \:\pm\: \sqrt{ (\frac {c} {2m})^2 \:-\: \frac {k} {m}}$$

(رابطه ۲)

بنابراین، پاسخ عمومی معادله، برابر با جمع جبری دو پاسخ $$\large x_1(t)$$ و $$\large x_2(t)$$ خواهد بود.

$$\large x_1(t) \:=\: C_1e^ {s_1t} \\~\\
\large x_2(t) \:=\: C_2e^ {s_2t} \\~\\
\large x(t) \:=\: C_1e^ {s_1t} \:+\: C_2e^ {s_2t} \\~\\
\large x(t) \:=\: C_1e^ {(-\:\frac {c} {2m} \:+\: \sqrt{(\frac {c} {2m})^2 \:-\: \frac {k}{m}})t} \:+\: C_2e^ {(-\:\frac {c} {2m} \:-\: \sqrt{(\frac {c} {2m})^2 \:-\: \frac {k}{m}})t}$$

(رابطه ۳)

در پاسخ عمومی بالا، $$\large C_1$$ و $$\large C_2$$ ثابت‌های دلخواهی هستند که مقدارشان با کمک شرایط اولیه سیستم تعیین می‌شود.

ثابت میرایی بحرانی و نسبت میرایی

میرایی بحرانی $$\large c_c$$ به عنوان مقدار مشخصی از ثابت میرایی $$\large c$$ تعریف می‌شود که برای آن، عبارت زیر رادیکال در رابطه ۲، برابر صفر باشد.

$$\large (\frac {c_c} {2m}) ^2\:- \:\frac {k} {m} \:=\:0 \\~\\
\large c_c \:=\: 2m\sqrt {\frac {k} {m}} \:=\: 2\sqrt{km} \:=\: 2m\omega_n$$

برای هر سیستم میرا، نسبت میرایی $$\large \zeta$$ را به عنوان نسبت ثابت میرایی به ثابت میرایی بحرانی تعریف می‌کنیم.

$$\large \zeta \:=\: c/c_c$$

با ادغام دو رابطه اخیر، می‌توانیم عبارت زیر را نتیجه بگیریم.

$$\large \frac {c} {2m} \:=\: \frac {c} {c_c} \times \frac {c_c} {2m} \:=\: \zeta \omega_n \\~\\
\large s_{1,2} \:=\: (-\: \zeta \:\pm\: \sqrt{ {\zeta}^2 \:-\: 1}) \omega_n$$

در نتیجه، پاسخ عمومی رابطه ۳ به شیوه زیر نوشته می‌شود.

$$\large x(t) \:=\: C_1e ^{(-\: \zeta \:+\: \sqrt {{\zeta}^2 \:-\: 1}) \omega_nt} \:+\: C_2e ^{(-\: \zeta \:-\: \sqrt {{\zeta}^2 \:-\: 1}) \omega_nt}$$

(رابطه ۴)

ماهیت ریشه‌های $$\large s_1$$ و $$\large s_2$$ و در نتیجه، رفتار این پاسخ، به بزرگی میرایی وابسته است. همان‌طور که مشاهده می‌کنید، در صورتی که $$\large \zeta \:=\:0$$، ارتعاشات نامیرا خواهیم داشت که این مورد در مقاله ارتعاشات آزاد سیستم‌های نامیرا به تفصیل مورد بررسی قرار گرفت. از این رو فرض می‌کنیم $$\large \zeta \:\neq \:0$$ باشد. حال، با سه حالت مختلف مواجه خواهیم شد که هریک از آنها را در ادامه بررسی می‌کنیم.

حالت اول: زیر میرایی

در این حالت که به عنوان حالت زیر میرایی (Under-Damped) شناخته می‌شود، میراگر ویسکوز به گونه‌ایست که ($$\large \zeta^2 \:-\:1$$) مقدار منفی دارد و ریشه‌های $$\large s_1$$ و $$\large s_2$$ به صورت زیر هستند.

$$\large s_1 \:=\: (-\: \zeta \:+\: i\sqrt{ 1\:-\: \zeta ^2}) \omega_n \\~\\
\large s_2 \:=\: (-\: \zeta \:-\: i\sqrt{ 1\:-\: \zeta ^2}) \omega_n$$

شرط حالت زیر میرایی این است که یکی از رابطه‌های زیر برقرار باشد. توجه کنید که تمام این رابطه‌ها معادل یکدیگرند.

$$\large \zeta \:< \:1$$ یا $$\large c \:< \:c_c$$ یا $$\large \frac {c} {2m} \:< \:\sqrt{ \frac {k} {m}}$$

اکنون می‌توانیم رابطه ۴ را به شکل متفاوت زیر بازنویسی کنیم.

$$\large x(t) \:=\: C_1e ^{(-\: \zeta \:+\: \sqrt {{\zeta}^2 \:-\: 1}) \omega_nt} \:+\: C_2e ^{(-\: \zeta \:-\: \sqrt {{\zeta}^2 \:-\: 1}) \omega_nt} \\~\\
\large =\: e^{-\: \zeta \omega_nt} [C_1e^{i\sqrt{1 \:-\: \zeta ^2} \omega_nt} \:+\: C_1e^{-\: i\sqrt{1 \:-\: \zeta ^2} \omega_nt}] \\~\\
\large =\: e^{-\: \zeta \omega_nt} [(C_1 \:+\: C_2) \cos (\sqrt{1 \:-\: \zeta^2} \omega_nt) \:+\: i(C_1 \:-\: C_2) \sin (\sqrt{1 \:-\: \zeta^2} \omega_nt)] \\~\\
\large =\: e^{-\: \zeta \omega_nt} [C^{ \prime}_1 \cos (\sqrt {1 \:-\: \zeta^2} \omega_nt) \:+\: C^{ \prime}_2 \sin (\sqrt {1 \:-\: \zeta^2} \omega_nt)] \\~\\
\large \Rightarrow x(t) \:=\: X_0 e^{-\: \zeta \omega_nt} \sin (\sqrt{1 \:-\: \zeta^2} \omega_nt \:+\: \phi_0) \\~\\
\large x(t) \:=\: X e^{-\: \zeta \omega_nt} \cos (\sqrt{1 \:-\: \zeta^2} \omega_nt \:-\: \phi)$$

در رابطه‌های بالا ($$\large C^{\prime} _{1}, \:C^{\prime} _{2}$$)، ($$\large X, \:\phi$$) و ($$\large X_0, \:\phi_0$$)، ثابت‌های دلخواهی هستند که باید با استفاده از شرایط اولیه، مقدار آنها تعیین شود. اگر شرایط اولیه را به صورت $$\large x(t \:=\: 0) \:=\: x_0$$ و $$\large \dot{x}(t \:=\: 0) \:=\: \dot{x}_0$$ فرض کنیم، ضرایب $$\large C^{\prime}_{1}$$ و $$\large C^{\prime}_{2}$$ به صورت زیر خواهند بود.

$$\large C^{\prime}_{1} \:=\: x_0 \\~\\
\large C^{\prime}_{2} \:=\: \frac {\dot{x}_0 \:+\: \zeta \omega_ nx_0} {\sqrt{ 1\:-\: \zeta^2} \omega_n}$$

اکنون می‌توانیم $$\large x(t)$$ را به صورت زیر بنویسیم.

$$\large x(t) \:=\: e^{-\: \zeta \omega _nt} [x_0 \cos (\sqrt{1 \:-\: \zeta ^2} \omega _nt) \:+\: \frac {\dot{x}_0 \:+\: \zeta \omega_n x_0} {\sqrt{1 \:-\: \zeta^2} \omega _nt} \sin (\sqrt{1 \:-\: \zeta^2} \omega _nt)]$$

(رابطه ۵)

همچنین می‌توانیم ثابت‌های ($$\large X, \:\phi$$) و ($$\large X_0, \:\phi_0$$) را به شکل زیر به دست آوریم.

$$\large X\:=\: X_0 \:=\: \sqrt{(C^{ \prime}_1) ^2\:+\: (C^{ \prime}_2) ^2} \:=\: \frac {\sqrt {x^2_0 \omega ^2_n \:+\: {\dot{x}} ^2_0 \:+\: 2x_0 \dot{x} \:\zeta \:\omega_n}} {\sqrt{1 \:-\: \zeta^2} \omega_n} \\~\\
\large \phi_0 \:=\: \tan ^{-1} (\frac {C^{ \prime}_1} {C^{ \prime}_2}) \:=\: \tan ^{-1} (\frac {x_0 \omega_n \sqrt{1 \:-\: \zeta^2}} {\dot{x}_0 \:+\: \zeta \omega _nx_0}) \\~\\
\large \phi \:=\: \tan ^{-1} (\frac {C^{ \prime}_2} {C^{ \prime}_1}) \:=\: \tan ^{-1} (\frac {\dot{x}_0 \:+\: \zeta \omega _nx_0} {x_0 \omega_n \sqrt{1 \:-\: \zeta^2}})$$

حرکت توصیف شده توسط رابطه ۵، یک حرکت هارمونیک میرا با فرکانس زاویه‌ای $$\large \sqrt {1 \:-\: \zeta ^2} \omega_n$$ است. ولی به دلیل وجود عامل $$\large e^{-\: \zeta \omega _nt}$$، با گذشت زمان، دامنه به صورت نمایی کاهش می‌یابد. شکل زیر را در نظر بگیرید. فرکانس ارتعاشات میرا به صورت زیر تعریف می‌شود.

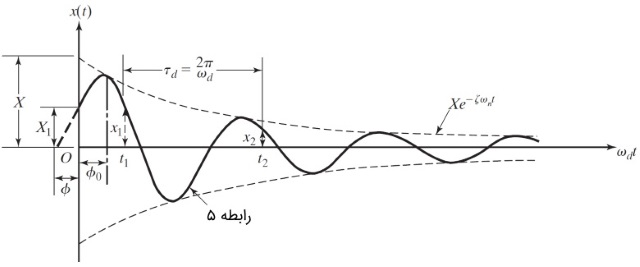
(شکل ۱)

$$\large \omega_d \:=\: \sqrt {1 \:-\: \zeta ^2} \omega_n$$

(رابطه ۶)

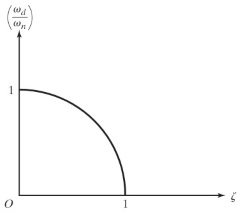
همان‌طور که ملاحظه می‌کنید، فرکانس ارتعاشات میرا ($$\large \omega_d$$) همیشه کوچکتر از فرکانس طبیعی نامیرا ($$\large \omega_n$$) است. شکل زیر، کاهش فرکانس ارتعاشات میرا را با افزایش مقدار میرایی، نشان داده است. در مبحث ارتعاشات مکانیکی، این حالت از اهمیت بسیار زیادی برخوردار است. زیرا تنها در این حالت است که حرکت نوسانی شکل می‌گیرد.

حالت دوم: میرایی بحرانی

در حالت دوم، سیستم همراه با میرایی بحرانی (Critically-Damped) است و ریشه‌های معادله نشان داده در رابطه ۲، به صورت زیر به دست می‌آید.

$$\large s_1 \:=\: s_2 \:=\: -\: \frac {c_c} {2m} \:=\: -\: \omega_n$$

شرط حالت میرایی بحرانی این است که یکی از رابطه‌های زیر برقرار باشد.

$$\large \zeta \:= \:1$$ یا $$\large c \:= \:c_c$$ یا $$\large \frac {c} {2m} \:= \:\sqrt{ \frac {k} {m}}$$

به دلیل وجود ریشه‌های تکراری، پاسخ رابطه شماره ۱ برابر با عبارت زیر است.

$$\large x(t) \:=\: (C_1 \:+\: C_2t) e^{-\: \omega_nt}$$

استفاده از شرایط اولیه $$\large x(t \:=\: 0) \:=\: x_0$$ و $$\large \dot{x}(t \:=\: 0) \:=\: \dot{x}_0$$ در رابطه بالا، نتایج زیر را به دنبال دارد.

$$\large C_1 \:=\: x_0 \\~\\
\large C_2 \:=\: \dot{x} _0\: +\:\omega _nx_0 \\~\\
\large \Rightarrow x(t) \:=\: [x_0 \:+\: (\dot{x}_0 \:+\: \omega_n x_0)t] e^{-\: \omega _nt}$$

با دقت در رابطه بالا درمی‌یابیم که هنگامی که $$\large t\: \rightarrow \:\infty$$، آنگاه $$\large e^{-\: \omega _nt} \:\rightarrow \:0$$ برقرار است. در نتیجه، مطابق آنچه در شکل زیر مشاهده می‌کنید، این حرکت، نوسانی نیست و در نهایت به مقدار صفر منتهی می‌شود.

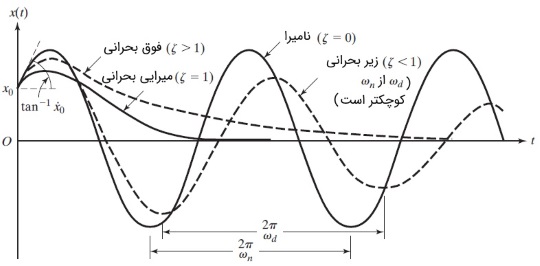
حالت سوم: فوق میرایی

در حالت سوم، سیستم در وضعیت فوق میرایی (Over-Damped) قرار دارد. میراگر ویسکوز به گونه‌ای است که عبارت $$\large \zeta^2 \:-\:1$$ بزرگتر از صفر است و ریشه‌های رابطه ۲، حقیقی و متفاوت از یکدیگر خواهند بود.

$$\large s_1 \:=\: (-\: \zeta \:+\: \sqrt{\zeta^2 \:-\:1}) \omega_n \:<\:0 \\~\\
\large s_2 \:=\: (-\: \zeta \:-\: \sqrt{\zeta^2 \:-\:1}) \omega_n \:<\:0$$

شرط حالت فوق میرایی این است که یکی از رابطه‌های زیر برقرار باشد.

$$\large \zeta \:> \:1$$ یا $$\large c \:> \:c_c$$ یا $$\large \frac {c} {2m} \:> \:\sqrt{ \frac {k} {m}}$$

در این صورت، پاسخ رابطه ۴ هم به شکل زیر است.

$$\large x(t) \:=\: C_1e^{(-\: \zeta \:+\: \sqrt{\zeta^2 \:-\:1}) \omega _nt} \:+\: C_2e^{(-\: \zeta \:-\: \sqrt{\zeta^2 \:-\:1}) \omega _nt}$$

(رابطه ۷)

اکنون با جایگذاری شرایط اولیه $$\large x(t \:=\: 0) \:=\: x_0$$ و $$\large \dot{x}(t \:=\: 0) \:=\: \dot{x}_0$$، می‌توانیم ثابت‌های $$\large C_1$$ و $$\large C_2$$ را به دست آوریم.

$$\large C_1 \:=\: \frac {x_0 \omega_n (\zeta \:+\: \sqrt{ \zeta^2 \:-\:1}) \:+\: \dot{x}_0} {2\omega_n \sqrt {\zeta ^2\: -\:1}} \\~\\
\large C_2 \:=\: \frac {-\: x_0 \omega_n (\zeta \:-\: \sqrt{ \zeta^2 \:-\:1}) \:-\: \dot{x}_0} {2\omega_n \sqrt {\zeta ^2\: -\:1}}$$

همان‌طور که دیدید، ریشه‌های $$\large s_1$$ و $$\large s_2$$ هر دو منفی هستند. به همین دلیل، مانند شکل قبل، تغییرات حرکت نسبت به زمان به صورت نمایی و نزولی است. بنابراین، رابطه ۷ حرکتی را نشان می‌دهد که مستقل از شرایط اولیه، رفتار نوسانی ندارد.

کاهش لگاریتمی

نرخ کاهش دامنه در ارتعاشات آزاد با میراگر ویسکوز را کاهش لگاریتمی (Logarithmic Decrement)‌ می‌نامند. این پارامتر به صورت لگاریتم طبیعی نسبت هر دو دامنه متوالی تعریف می‌شود. فرض کنید $$\large t_1$$ و $$\large t_2$$ زمان متناظر با دو دامنه متوالی را نشان دهند که به فاصله یک سیکل کامل و برای سیستم زیر میرایی اندازه‌گیری شده‌اند. شکل شماره ۱ را بار دیگر مشاهده کنید. نسبت این دو دامنه به صورت زیر است.

$$\large \frac {x_1} {x_2} \:=\: \frac {X_0 e^{-\:\zeta \omega _nt_1} \cos (\omega_dt_1 \:-\: \phi_0)} {X_0 e^{-\:\zeta \omega _nt_2} \cos (\omega_dt_2 \:-\: \phi_0)}$$

ولی می‌دانیم بین $$\large t_1$$ و $$\large t_2$$ رابطه $$\large t_2 \:=\: t_1 \:+\: \tau_d$$ برقرار است. در این رابطه دامنه ارتعاشات میرا به صورت $$\large \tau_d \:=\: 2\pi /\omega_d$$ تعریف می‌شود. از این رو، نسبت بالا را به صورت زیر می‌نویسیم.

$$\large \cos (\omega_dt_2 \:-\: \phi_0) \:=\: \cos (2\pi \:+\: \omega_d t_1 \:-\: \phi_0) \:=\: \cos (\omega_d t_1 \:-\: \phi_0) \\~\\
\large \frac {x_1} {x_2} \:=\: \frac {e^{-\:\zeta \omega _nt _1}} {e^{-\:\zeta \omega _n( t_1 \:+\: \tau_d)}} \:=\: e^{ \zeta \omega _n\tau _d}$$

کاهش لگاریتمی با $$\large \delta$$ نمایش داده شده و به صورت زیر نوشته می‌شود.

$$\large \delta \:=\: \ln \frac {x_1} {x_2} \:=\: \zeta \omega _n\tau _d \:=\: \zeta \omega _n \frac {2\pi} {\sqrt {1 \:-\: \zeta^2} \omega_n} \\~\\
\large \delta \:=\: \frac {2\pi \zeta} {\sqrt {1 \:-\: \zeta ^2}} \:=\: \frac {2\pi} {\omega_d} \times \frac {c} {2m}$$

(رابطه ۸)

مطابق این رابطه، اگر میرایی سیستم خیلی کوچک باشد ($$\large \zeta \ll 1$$)، می‌توانیم از تقریب زیر استفاده کنیم.

$$\large \delta \:\cong\: 2\pi \zeta$$

(رابطه ۹)

تغییرات کاهش لگاریتمی $$\large \delta$$ برحسب $$\large \zeta$$ براساس دو رابطه ۸ و ۹ را می‌توانید در شکل زیر مشاهده کنید. همان‌طور که می‌بینید، برای مقادیر کمتر از $$\large \zeta \:=\: 0.3$$، تمایز دو نمودار از یکدیگر مشکل است.

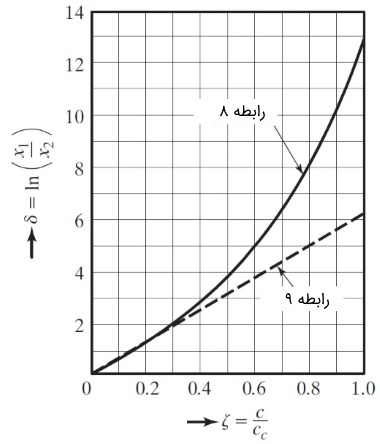
کاهش لگاریتمی یک پارامتر بی‌بُعد بوده و در واقع، بیان دیگری از نسبت میرایی $$\large \zeta$$ است. اگر $$\large \delta$$ معلوم باشد، با کمک رابطه 8 می‌توانیم $$\large \zeta$$ را بیابیم.

$$\large \zeta \:=\: \frac {\delta} {\sqrt {(2 \pi) ^2 \:+\: \delta ^2}}$$

(رابطه ۱۰)

اگر از رابطه ۹ استفاده کنیم، $$\large \zeta$$ به صورت زیر تبدیل می‌شود.

$$\large \zeta \:\cong\: \frac {\delta} {2 \pi}$$

در صورتی که میرایی سیستم مشخص نباشد، می‌توانیم آن را با اندازه‌گیری هر دو دامنه متوالی $$\large x_1$$ و $$\large x_2$$ به دست آوریم. ابتدا با محاسبه لگاریتم طبیعی نسبت این دو عدد، مقدار $$\large \delta$$ را می‌یابیم و سپس با استفاده از رابطه ۱۰، نسبت میرایی $$\large \zeta$$ را محاسبه میکنیم. در واقع، اگر دو دامنه مختلف از نمودار را داشته باشیم که بین آنها، چندین سیکل کامل انجام شده باشد، باز هم می‌توانیم $$\large \zeta$$ را پیدا کنیم. فرض کنید $$\large x_1$$ و $$\large x_{m+1}$$، دامنه متناظر با زمان‌های $$\large t_1$$ و $$\large t_{m+1} =t_1+m\tau_d$$ باشد و بدانیم که $$\large m$$ یک عدد صحیح است. در این صورت میتوانیم روابط زیر را بنویسیم.

$$\large \frac {x_1} {x_{m+1}} \:=\: \frac {x_1} {x_2} \times \frac {x_2} {x_3}\times \frac {x_3} {x_4} \times … \times \frac {x_m} {x_{m+1}}$$

از آنجایی که هر دو دامنه متوالی در رابطه $$\large \frac {x_j} {x_{j+1}} \:=\: e^{ \zeta \omega_n \tau_d}$$ صدق می‌کنند، رابطه بالا به شیوه زیر ساده می‌شود.

$$e^{ \zeta \omega_n \tau_d}$$

اکنون از رابطه ۸ کمک می‌گیریم تا مقدار $$\large \delta$$ مشخص شود.

$$\large \delta \:=\: \frac {1} {m} \ln(\frac {x_1} {x_{m+1}})$$

اتلاف انرژی در میراگر ویسکوز

برای نشان دادن نرخ تغییرات انرژی در یک سیستم میراگر ویسکوز با زمان ($$\large dW/dt$$)، عبارت زیر را تعریف می‌کنیم.

$$\large \frac {dW} {dt} \:=\: Fv \:=\: -\:c v^2 \:=\: -\:c (\frac {dx} {dt })^2$$

علامت منفی در رابطه بالا، اتلاف انرژی با زمان را نشان می‌دهد. حرکت هارمونیک ساده‌ای را مطابق رابطه $$\large x(t) \:=\: X\sin \omega _dt$$ در نظر بگیرید. در این رابطه $$\large X$$ دامنه حرکت است و انرژی تلف شده در یک سیکل کامل به صورت زیر خواهد بود.

$$\large \Delta W\:=\: \int_{t=0}^{(2\pi/\omega_d)} c(\frac{\text {d}x}{\text {d}t}) ^2dt \:=\: \int_{0}^{2\pi} cX^2\omega_d \cos^2 \omega _dt.d (\omega_dt) \\~\\
\large \Rightarrow ~~~ \Delta W\:=\: \pi c \omega_d X^2$$

(رابطه ۱۱)

نتیجه انتگرال بالا نشان می‌دهد انرژی تلف شده با مربع دامنه حرکت متناسب است. توجه کنید که مقدار $$\large \Delta W$$ تابعی از فرکانس $$\large \omega_d$$ است و نمی‌تواند برای مقادیر میرایی مختلف و دامنه مشخص، ثابت باقی بماند.

حتی اگر مطابق شکل زیر، فنری با سفتی $$\large k$$ موازی با میراگر ویسکوز به کار گرفته شود، باز هم رابطه ۱۱ برقرار است. شکل زیر را در نظر بگیرید. نیروی بازدارنده حرکت را می‌توان به این گونه تعریف کرد.

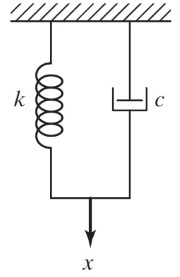
$$\large F \:=\: -\:kx \:-\: cv \:=\: -\:kx \:-\: c\dot{x}$$

(رابطه 12)

در حرکت هارمونیک ساده رابطه زیر برقرار است.

$$\large x(t) \:=\: X \sin \omega _dt$$

به این ترتیب، رابطه ۱۲ به شکل زیر نوشته می‌شود.

$$\large F \:=\: -\:kX \sin \omega _dt \:-\: c\omega_d X\cos \omega _dt$$

سپس، انرژی تلف شده در یک سیکل کامل را به دست می‌آوریم.

$$\large \Delta W\:=\: \int_ {t=0} ^{2\pi/\omega_d} Fv\: \text{d}t \\~\\
\large \:=\: \int_ {0} ^{2\pi /\omega _dt} kX^2 \omega _d\sin \omega _dt\:.\cos \omega _dt\: .\text{d} (\omega _dt) \\~\\
\large \:+\: \int_ {0} ^{2\pi /\omega _dt} c\omega _dX^2 \: \cos^2 \omega _dt \:. \text{d} (\omega _dt) \\~\\
\large \Rightarrow ~~~ \Delta W \:=\: \pi c \omega_d X^2$$

همان گونه که مشاهده می‌کنید، رابطه به دست آمده مشابه رابطه ۱۱ است. این نتیجه، مورد انتظار بود. زیرا کار خالص انجام شده توسط نیروی فنر در یک یا چند سیکل کامل برابر صفر است. همچنین می‌توانیم کسری از انرژی کل سیستم ارتعاشی را که تلف می‌شود، در هر سیکل ($$\large \Delta W/W$$) به دست آوریم. انرژی کل سیستم ($$\large W$$)، به صورت انرژی پتانسیل ماکسیمم ($$\large \frac {1} {2} kX^2$$) یا انرژی جنبشی ماکسیمم ($$\large \frac {1} {2} mv^2_{max} \:=\: \frac {1} {2} mX^2 \omega^2_d$$) نشان داده می‌شود. هنگامی که ضریب میرایی کوچک باشد، این دو مقدار تقریباً با هم برابرند. بنابراین رابطه زیر را می‌نویسیم.

$$\large \frac {\Delta W} {W} \:=\: \frac {\pi c \omega_d X^2} {\frac {1} {2} m \omega^2_d X^2} \:=\: 2(\frac {2\pi} {\omega_d}) (\frac {c} {2m}) \:=\: 2\delta \:\approx\: 4\pi \zeta$$

نسبت $$\large \frac {\Delta W} {W}$$، ظرفیت میرایی ویژه (Specific Damping Capacity) نامیده می‌شود و مقدار آن ثابت است. برای مقایسه ظرفیت میرایی در مواد مهندسی از این عدد استفاده می‌شود. کمیت دیگری که برای مقایسه ظرفیت میرایی مورد استفاده قرار می‌گیرد، ضریب افت (Loss Coefficient) نام دارد. ضریب افت به عنوان نسبت انرژی تلف شده در هر رادیان به انرژی کل تعریف می‌شود و در رابطه زیر با $$\large C_{loss}$$ نشان داده شده است.

$$\large C_{loss} \:=\: \frac {\Delta W/2 \pi} {W} \:=\: \frac {\Delta W} {2\pi W}$$

سیستم‌های پیچشی با میراگر ویسکوز

تا اینجا، روش‌های ارائه شده مربوط به ارتعاشات خطی با میراگر ویسکوز بودند. اما می‌توان همین روابط را برای ارتعاشات پیچشی با میراگر ویسکوز نیز توسعه داد. بدین منظور سیستم پیچشی یک درجه آزادی با میراگر ویسکوز را مطابق شکل زیر در نظر بگیرید. گشتاور میرایی لزجی به صورت زیر تعریف می‌شود.

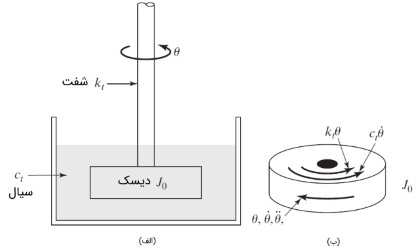
$$\large T \:=\: -\:c_t \dot {\theta}$$

در رابطه بالا، $$\large c_t$$ ثابت میراگر ویسکوز در حرکت پیچشی و $$\large \dot {\theta} \:=\: \text {d} \theta/ \text {d}t$$ سرعت زاویه دیسک است. علامت منفی، نشان می‌دهد گشتاور میرایی در خلاف جهت سرعت زاویه‌ای وارد می‌شود. معادله حرکت به شکل زیر استخراج می‌شود.

$$\large J_0 \ddot {\theta} \:+\: c_t \dot {\theta} \:+\: k_t \theta \:=\: 0$$

ممان اینرسی دیسک و جابجایی زاویه‌ای دیسک، به ترتیب با $$\large J_0$$ و $$\large \theta$$ نشان داده شده است. $$\large k_t$$ ثابت فنر سیستم (معادل گشتاور بازدارنده در جابجایی زاویه‌ای واحد)‌ است. حل معادله بالا، عیناً مانند همان معادله‌ای است که در حرکت خطی بررسی کردیم. به عنوان مثال، در حالت زیر میرایی، فرکانس ارتعاشات میرا شونده برابر با عبارت زیر است.

$$\large \omega _d\: =\: \sqrt{1 \:-\: \zeta^2} \omega_n \\~\\
\large \omega_n \:=\: \sqrt{ \frac {k_t} {J_0}} \\~\\
\large \zeta \:=\: \frac {c_t} {c_{tc}} \:=\: \frac {c_t} {2J_0 \omega _n} \:=\: \frac {c_t} {2\sqrt {k_t J_0}}$$

$$\large c_{tc}$$ ثابت میرایی بحرانی در حرکت پیچشی نام دارد.

مثال ۱- پاسخ سندان در چکش آهنگری با میراگر ویسکوز

سؤال: وزن سندان در یک چکش آهنگری برابر $$\large 5000 \:N$$ بوده و روی پایه‌ای با سفتی $$\large 5\times 10^6 \:N/m$$ و ضریب میراگر ویسکوز $$\large 10,000 \:N-s/m$$ قرار گرفته است. در فرآیند آهنگری، چکش که در شکل زیر با $$\large m$$ نشان داده شده است، $$\large 1000\:N$$ وزن دارد و از ارتفاع $$\large 2\:m$$ روی سندان ($$\large M$$) می‌افتد. اگر پیش از ضربه، سندان در حالت تعادل باشد، پاسخ سندان را پس از ضربه مشخص کنید. ضریب برجهندگی (Coefficient of Restitution) به صورت زیر تعریف می‌شود و مقدار آن را در این مسأله برابر $$\large 0.4$$ فرض کنید.

$$\large r \:=\: -\: \frac {V_{a2} \:-\: V_{t2}} {V_{a1} \:-\: V_{t1}}$$

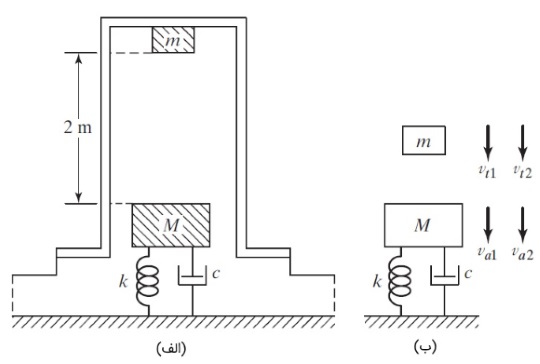
پاسخ: ابتدا از تعریف قانون پایستگی ممنتوم و ضریب برجهندگی استفاده می‌کنیم تا سرعت اولیه سندان را به دست بیاوریم. سرعت چکش را قبل و بعد از برخورد با سندان، به ترتیب با $$\large v_{t1}$$ و $$\large v_{t2}$$ نشان داده‌ایم. به صورت مشابه، سرعت سندان نیز قبل و بعد از برخورد، به ترتیب $$\large v_{a1}$$ و $$\large v_{a2}$$ است. جابجایی سندان، نسبت به موقعیتش در تعادل استاتیکی سنجیده می‌شود و سرعت‌های رو به پایین را مثبت فرض می‌کنیم. اصل پایستگی ممنتوم را برای سیستم می‌نویسیم.

$$\large M( v_{a2} \:-\: v_{a1}) \:=\: m( v_{t1} \:-\: v_{t2})$$

پیش از برخورد، سندان در حالت تعادل است. پس مقدار $$\large v_{a1}$$ را صفر قرار می‌دهیم. برای پیدا کردن $$\large v_{t1}$$، انرژی جنبشی چکش را درست در لحظه پیش از برخورد، برابر انرژی پتانسیل آن پیش از رها شدن از ارتفاع $$\large h \:=\: 2\:m$$ می‌نویسیم.

$$\large \frac {1} {2} m v^2_{t1} \:=\: mgh \\~\\
\large v_{t1} \:=\: \sqrt{2gh} \:=\: \sqrt{ 2\times 9.81 \times2} \:=\: 6.26099 \:m/s$$

حال، مقدار به دست آمده را در قانون پایستگی ممنتوم جایگذاری می‌کنیم.

$$\large \frac {5000} {9.81} (v_{a2} \:-\: 0) \:=\: \frac {1000} {9.81} ( 6.26099 \:-\: v_{t2}) \\~\\
\large 510.204082 \: v_{a2} \:=\: 638.87653 \:-\: 102.040813 \:v_{t2}$$

در ادامه، از ضریب برجهندگی استفاده می‌کنیم تا معادله دو مجهولی دوم هم مشخص شود.

$$\large r \:=\: -\: \frac {V_{a2} \:-\: V_{t2}} {V_{a1} \:-\: V_{t1}} \:=\: 0.4 \\~\\
\large \Rightarrow ~~~ -\: \frac {V_{a2} \:-\: V_{t2}} {0 \:-\: 6.26099} \:=\: 0.4 \\~\\
\large v_{a2} \:=\: v_{t2} \:+\: 2.504396$$

اکنون دو معادله با دو مجهول $$\large v_{a2}$$ و $$\large v_{t2}$$ داریم که با حل آنها نتایج زیر به دست می‌آید.

$$\large v_{a2} \:=\: 1.460898 \:m/s \\~\\
\large v_{t2} \:=\: -\: 1.043498 \:m/s$$

بنابراین شرایط اولیه سندان به صورت زیر است.

$$\large x_0 \:=\: 0 \\~\\
\large \dot{x}_0 \:=\: 1.460898 \:m/s$$

برای محاسبه ضریب میرایی به شیوه زیر عمل می‌کنیم.

$$\large \zeta \:=\: \frac {c} {2\sqrt {kM}} \:=\: \frac {1000} {2\sqrt {(5\times 10^6) (\frac {5000} {9.81})}} \:=\: 0.0989949$$

حال، می‌توانیم فرکانس‌های طبیعی نامیرا و میرا شونده سندان را محاسبه کنیم.

$$\large \omega_n \:=\: \sqrt{ \frac {k} {M}} \:=\: \sqrt{ \frac {5 \times 10^6} {(\frac {5000} {9.81} )}} \:=\: 98.994949 \:rad/s \\~\\
\large \omega_d \:=\: \omega_n \sqrt{ 1\:-\: \zeta^2} \:=\: 98.994949 \sqrt {1\:-\: (0.0989949) ^2}\\~\\
\large \Rightarrow ~~~ \omega_d \:=\: 98.024799 \:rad/s$$

با جایگذاری این مقادیر در رابطه ۵، نتیجه زیر حاصل می‌شود.

$$\large x(t) \:=\: e^{-\zeta \omega _nt} (\frac {\dot{x}_0} {\omega_d} \sin \omega _dt) \\~\\
\large =\: e^{-9.799995\:t} (0.01490335 \:\sin 98.024799 \:t) ~~~ m$$

مثال ۲- جاذب ضربه در موتورسیکلت با میراگر ویسکوز

سؤال: می‌خواهیم برای موتورسیکلتی به جرم $$\large 200 \:kg$$، جاذب ضربه زیر میرایی طراحی کنیم. شکل زیر را در نظر بگیرید. هنگامی که جاذب ضربه، به دلیل دست‌انداز جاده‌ای، در معرض سرعت اولیه در راستای عمودی قرار می‌گیرد، منحنی جابجایی–زمان به صورت زیر خواهد بود. اگر دوره ارتعاش میرا شونده $$\large 2 \:s$$ باشد و دامنه $$\large x_1$$ در فاصله نیم‌سیکل به یک‌چهارم ($$\large x_{1.5} \:=\: x_1 /4$$) برسد، ضرایب سفتی و میرایی را بیابید. همچنین سرعت اولیه مینیمم که به جابجایی ماکسیمم $$\large 250 \:mm$$ منجر می‌شود را تعیین کنید.

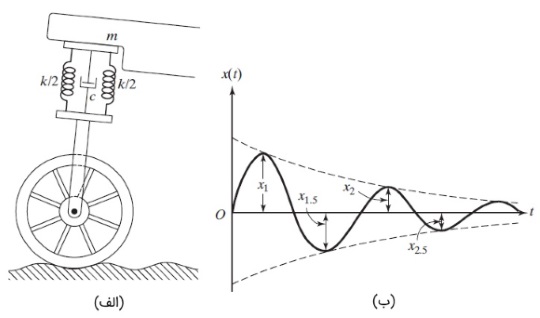
پاسخ: برای به دست آوردن کاهش لگاریتمی به طریق زیر عمل می‌کنیم.

$$\large x_{1.5} \:=\: \frac {x_1} {4} \\~\\
\large x_2 \:=\: \frac {x_{1.5}} {4} \:=\: \frac {x_1} {16} \\~\\
\large \delta \:=\: \ln (\frac {x_1} {x_2}) \:=\: \ln(16) \:=\: 2.7726 \:=\: \frac {2\pi \zeta} {\sqrt {1\:-\: \zeta^2}}$$

با حل این معادله، مقدار $$\large \zeta \:=\: 0.4037$$ به دست می‌آید. دوره میرایی ارتعاش برابر $$\large 2 \:s$$ است. در نتیجه می‌توانیم فرکانس طبیعی را پیدا کنیم.

$$\large 2 \:=\: \tau_d \:=\: \frac {2\pi} {\omega_d} \:=\: \frac {2\pi} {\omega_n \sqrt{1 \:-\: \zeta^2}} \\~\\
\large \omega_n \:=\: \frac {2\pi} {2\sqrt{1 \:-\: (0.4037)^2}} \:=\: 3.4338 \:rad/s$$

اکنون ضریب میرایی و ضریب میرایی بحرانی را محاسبه می‌کنیم.

$$\large c_c \:=\: 2m\omega_n \:=\: 2(200) (3.4338) \:=\: 1373.54 \:N-s/m \\~\\
\large c \:=\: \zeta c_c \:=\: (0.4037) (1373.54) \:=\: 554.4981 \:N-s/m$$

در مرحله بعد، سفتی فنر را به دست می‌آوریم.

$$\large k \:=\: m\omega ^2_n \:=\: (200) (3.4338)^2 \:=\: 2358.2652 \:N/m$$

ماکسیمم جابجایی جرم، در لحظه $$\large t_1$$ رخ می‌دهد.

$$\large \sin \omega _dt_1 \:=\: \sqrt {1 \:-\: \zeta^2} \\~\\
\large \sin \omega _dt_1 \:=\: \sin \pi t_1 \:=\: \sqrt {1 \:-\: (0.4037)^2} \:=\: 0.9149 \\~\\
\large \Rightarrow \:=\: t_1 \:=\: \frac {\sin ^{-1} (0.9149)} {\pi} \:=\: 0.3678 \:sec$$

می‌توان نشان داد که منحنی گذرنده از نقاط ماکسیمم و مینیمم، از رابطه زیر پیروی می‌کنند.

$$\large x\:=\: \sqrt{1 \:-\: \zeta^2} Xe^ {-\zeta \omega _nt}$$

می‌دانیم مقدار جابجایی ماکسیمم برابر با $$\large x\:=\: 250 \:mm$$ است.

$$\large 0.25\:=\: \sqrt{1 \:-\: (0.4037)^2} Xe^ {-(0.4037) (3.4338) (0.3678)} \\~\\
\large \Rightarrow ~~~ X \:=\: 0.4550 \:m$$

با مشتق‌گیری از رابطه جابجایی، سرعت جرم به دست می‌آید.

$$\large x(t) \:=\: Xe^{-\:\zeta \omega _nt} \sin \omega _dt \\~\\
\large \dot{x} (t) \:=\: Xe^{-\:\zeta \omega _nt} (-\:\zeta \omega_n \sin \omega _dt \:+\: \omega_d \cos \omega _dt)$$

هنگامی که $$\large t \:=\: 0$$ باشد، سرعت به صورت زیر محاسبه می‌شود.

$$\large \dot{x}(t \:=\: 0) \:=\: \dot{x} _0\:=\: X\omega_d \:=\: X\omega_n \sqrt{1 \:-\: \zeta^2} \\~\\
\large \:=\: (0.4550) (3.4338) \sqrt{1 \:-\: (0.4037)^2} \:=\: 1.4294 \:m/s$$

مثال ۳- تحلیل عملکرد توپ جنگی با میراگر ویسکوز

سؤال: نمودار شماتیک مربوط به یک نمونه توپ جنگی را در شکل زیر مشاهده می‌کنید. هنگامی که گلوله (پرتابه)‌ شلیک می‌شود، گازهای پرفشار داخل لوله، سرعت پرتابه را تا حد زیادی بالا می‌برند. برای اینکه پس از شلیک، لوله توپ بدون نوسان و در کمترین زمان ممکن به حالت ساکن برگردد، از یک سیستم فنر و میراگر ویسکوز استفاده شده است. فرض کنید مجموع جرم لوله توپ و سیستم فنر و میراگر برابر $$\large 500 \:kg$$ باشد. اگر سفتی فنر $$\large 10,000 \:N/m$$ و جابجایی مکانیزم فنر و میراگر در لحظه شلیک $$\large 0.4 \:m$$ باشد، موارد زیر را تعیین کنید.

الف) ضریب میرایی بحرانی

ب) سرعت اولیه سیستم فنر و میراگر

پ) زمان لازم برای بازگشت به موقعیت $$\large 0.1 \:m$$ از موقعیت آغازین

پاسخ: الف) ابتدا فرکانس طبیعی نامیرا و سپس ضریب میرایی بحرانی را محاسبه می‌کنیم.

$$\large \omega _n\:=\: \sqrt {\frac {k} {m}} \:=\: \sqrt{ \frac {10,000} {500}} \:=\: 4.4721 \:rad/s \\~\\
\large c_c \:=\: 2m \omega_n \:=\: 2(500) (4.4721) \:=\: 4472.1 \:N-s/m$$

ب) پاسخ سیستم میرا شونده با میرایی بحرانی با رابطه زیر تعریف می‌شود.

$$\large x(t) \:=\: (C_1 \:+\: C_2t) e^{ -\:\omega _nt}$$

که در رابطه بالا، ضرایب $$\large C_1$$ و $$\large C_2$$ به ترتیب برابر $$\large x_0$$ و $$\large \dot{x}_0 \:+\: \omega_n x_0$$ هستند. زمان $$\large t_1$$ که در آن، $$\large x(t)$$ به مقدار ماکسیمم می‌رسد را می‌توانیم با حل معادله زیر به دست بیاوریم.

$$\large \dot{x}(t) \:=\: C_2 e^{ -\:\omega _nt} \:-\: \omega_n (C_1 \:+\: C_2t) e^{ -\:\omega _nt} \\~\\
\large \dot{x}(t) \:=\: 0\\~\\
\large \Rightarrow ~~~ t_1 \:=\: (\frac {1} {\omega_n} \:-\: \frac {C_1} {C_2})$$

در این حالت، رابطه $$\large x_0 \:=\: C_1 \:=\:0$$ برقرار است. از این رو رابطه بالا به صورت زیر خلاصه می‌شود.

$$\large t_1 \:=\: 1/ \omega_n$$

از طرفی، مقدار ماکسیمم $$\large x(t)$$ هم در صورت مسأله داده شده است.

$$\large x_{max} \:=\: 0.4m \\~\\
\large x_{max} \:=\: x(t \:=\: t_1) \;=\: C_2t_1 e^{ -\:\omega _nt_1} \:=\: \frac {\dot {x}_0} {\omega_n} e^{-1} \:=\: \frac {\dot {x}_0} {e\omega _n} \\~\\
\large \dot {x}_0 \:=\: x_{max} \omega _ne \:=\: (0.4) (4.4721) (2.7183) \:=\: 4.8626 \:m/s$$

پ) اگر $$\large t_2$$ را زمانی فرض کنیم که توپ نسبت به موقعیت اولیه‌اش در موقعیت $$\large 0.1 \:m$$ قرار گرفته باشد، برای محاسبه آن به شکل زیر عمل می‌کنیم.

$$\large 0.1 \:=\: C_2t_ 2e^ {-\: \omega _nt _2} \:=\: 4.8626\:t_2e^{-(\: 4.4721 \:t_2)} \\~\\
\large \Rightarrow ~~~ t_2 \:=\: 0.8258 \:s$$

اگر به مباحث مرتبط در زمینه مکانیک و ارتعاشات علاقه‌مند هستید، آموزش‌های زیر به شما پیشنهاد می‌شوند:

• مجموعه آموزش های مهندسی مکانیک
• مجموعه آموزش‌های نرم‌افزارهای مهندسی مکانیک
• آموزش ارتعاشات مکانیکی همراه با حل مثال در متلب (MATLAB)
• آموزش ارتعاشات مکانیکی (مرور و حل تست کنکور ارشد)
• ژیروسکوپ – از صفر تا صد
• ارتعاشات آزاد در سیستم های نامیرا – از صفر تا صد
• ارتعاشات مکانیکی — بخش سوم: سیستم‌های دو درجه آزادی

^^