لختی دورانی چیست؟ — به زبان ساده

به توانایی اجسام مختلف در دوران، «لَختی دورانی» (Rotational Inertia) یا «ممان اینرسی» (Moment of Inertia) گفته می‌شود. این مقدار یک عدد اسکالر است که قابلیت یک جسم در تغییر سرعت دورانش حول یک محور خاص را نشان می‌دهد. لختی دورانی نقشی مشابه با جرم را در مکانیک دورانی ایفا می‌کند. این ویژگی به دو عامل جرم و شکل توزیع آن حول محور مد نظر وابسته است.

به منظور درک بهتر، تصور کنید سنگی را به طنابی بسته‌اید و آن را حول سر خود و با سرعت دورانی مشخصی می‌چرخانید. اگر بخواهید با طول بلند‌تری از طناب، همان سنگ را با همان سرعت بچرخانید، به انرژی بیشتری نیاز خواهید داشت. (می‌توانید این آزمایش ساده را انجام دهید.) چنین اتفاقی به این علت رخ می‌دهد که جرمی که در فاصله بیشتری از شما (محور دوران، بدن خودتان است) قرار دارد، دارای لختی دورانی بیشتری است.

لختی دورانی را با نماد I نشان می‌دهند. در شکل بالا، این مقدار برابر است با:

I=mr²

توجه داشته باشید که واحد این مقدار معادل با kg⋅m² در نظر گرفته می‌شود. لختی دورانی را با نام «گشتاور اینرسی» (Moment of Inertia) نیز می‌شناسند. هم‌چنین در بعضی از متون، از این ویژگی به عنوان گشتاور دوم اینرسی، یاد می‌شود. دلیل عبارت «دوم» در این نامگذاری، وابسته بودن آن به توان دوم فاصله است.

ارتباط میان لختی دورانی و قانون دوم نیوتن

همان‌طور که در بالا نیز بیان شد، لختی دورانی، نقش جرم را در نسخه دورانی قانون دوم نیوتن ایفا می‌کند. [این جمله به این معنی است که اگر بخواهیم قانون دوم نیوتن را به‌صورت دورانی بنویسیم، لختی دورانی، نقش جرم را ایفا می‌کند.

فیلم آموزش استاتیک – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

حال اجازه دهید تا این قانون را در قالب مکانیک دورانی بنویسیم. بدین منظور مطابق شکل زیر، جرم m را تصور کنید که به نخی به شعاع r متصل شده و حول مرکزش دوران می‌کند.

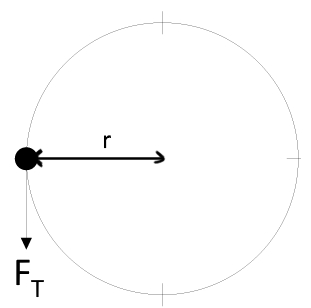
با فرض این‌که نیروی اعمال شده به سیستم برابر با F_T باشد، قانون دوم نیوتن را می‌توان بصورت زیر بیان کرد:

F_T​=ma_T

سرعت دورانی این سیستم با گذشت زمان در حال افزایش است؛ از طرفی رابطه بین شتاب خطی و شتاب زاویه‌ای به شکل زیر است:

(r) شعاع × (α) شتاب زاویه‌ای=شتاب خطی (a_T)

بنابراین با ترکیب دو رابطه بالا خواهیم داشت:

(F_T​=m(rα

در مکانیک دورانی، گشتاور، معادل نیرو در مکانیک خطی است، در نتیجه با ضرب طرفین رابطه بالا در r می‌توان نوشت:

(F_Tr​=mr(rα

τ=mr²α

τ=Iα

فرمول τ=Iα، در واقع همان قانون دوم نیوتن در مکانیک دورانی است. احتمالا متوجه شده‌اید که در این فرمول گشتاور معادل با نیرو، شتاب زاویه‌ای معادل با شتاب خطی و لختی دورانی معادل با جرم است. مثال‌های زیر احتمالا در درک بهتر موضوع کمک‌ کننده باشند.

مثال 1

موتوری قادر است تا گشتاور ثابت 100 نیوتن.متر و سرعت دورانیِ ماکزیمم 150 رادیان بر ثانیه را ایجاد کند. این موتور به چرخی آهنین با لختی دورانی 0.1kg.m² متصل شده. شتاب زاویه‌ای چرخ، هنگامی که موتور روشن شود چقدر است؟ چه مدت زمانی طول می‌کشد تا چرخ به سرعت زاویه‌ای مذکور برسد؟

فرضیات مسئله:

τ= 100N.m

I=0.1kg.m²

با جایگذاری این مقادیر در قانون دوم نیوتن در حالت دورانی خواهیم داشت:

τ=Iα

100=0.1×α

α=1000

بنابراین با بدست آمدن شتاب زاویه‌ای و داشتن بیشترین سرعت زاویه‌ای، زمان لازم به منظور رسیدن به سرعت مفروض بدست خواهد آمد.

ω=αt

150=1000t

ثانیه t=0.15

در نتیجه زمان لازم برای رسیدن به این سرعت زاویه‌ای برابر با 0.15 ثانیه خواهد بود.

محاسبه لختی دورانی در حالت کلی

معمولاً سیستم‌های مکانیکی شامل بخش‌های مختلفی هستند که به یکدیگر متصل شده‌اند. به یاد داشته باشید که لختی دورانی برای هر سیستمی قابل تعریف است. به‌منظور محاسبه لختی دورانی در ابتدا بایستی محور دوران مشخص شود.

فیلم آموزش ایستایی (استاتیک) – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

سیستمی را تصور کنید که از تعدادی جرم m_i تشکیل شده است. فرض کنید r_i، فاصله هر‌کدام از آن‌ها از محور دوران باشد. با جمع کردن لختی‌های با یکدیگر، لختی دورانی کل مجموعه محاسبه می‌شود. بنابراین اگر I نشان دهنده لختی چنین سیستمی باشد، رابطه زیر برقرار خواهد بود:

I​=m_1​r₁^2​+m_2​r₂^2​+…=Σm_i​r_i^2​​

محاسبه لختی دورانی اَشکال پیچیده

به منظور محاسبه لختی دورانی اشکال پیچیده بایستی از مفاهیم ریاضیات بهره برد؛ اما در بسیاری از متون علمی، جدوالی با هدف محاسبه لختی دورانی اجسام متداول موجود است. در این جدول‌ها، لختی دورانی، حول مرکزِ جرم آن‌ها بیان شده است.

فیلم آموزش مکانیک تحلیلی 2 – جامع و کاربردی در فرادرس

کلیک کنید

به‌عنوان مثال لختی دورانی یک استوانه صُلب حول محورش برابر است با:

I=1/2mr²

هم‌چنین برای استوانه‌ای به جرم m که شعاع داخلی و خارجی آن به ترتیب برابر با r_i و r_o باشد:

در شکل‌های زیر این مقدار برای برخی از جسم‌های پرکاربرد نشان داده شده‌ است.

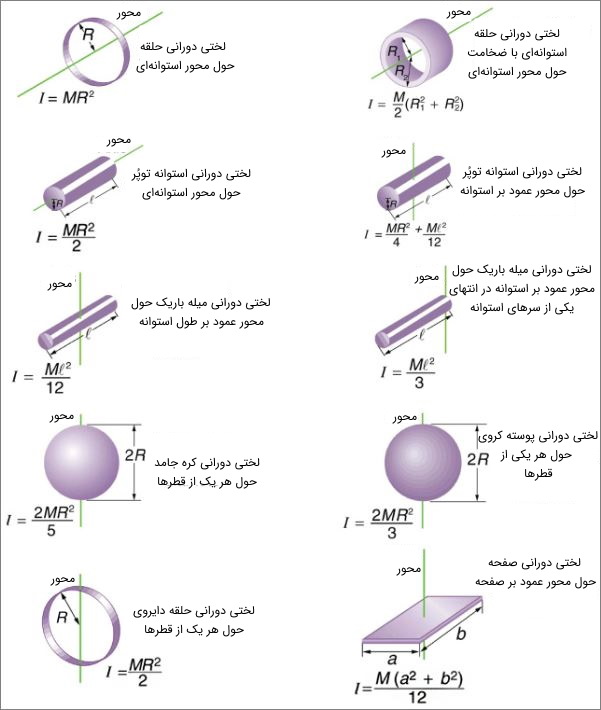
توجه داشته‌ باشید که لختی دورانی اکثر شکل‌های پیچیده را می‌توان بصورت ترکیبی از اشکال ساده‌تر بیان کرد؛ اما مشکلی که در بعضی مواقع با آن روبرو می‌شویم این است که برخی اوقات هدف ما محاسبه لختی دورانی، حول محور دیگری است. در چنین مواقعی، می‌توان از «قضیه محورهای موازی» (Parallel Axis Theorem) استفاده کرد.

قضیه محورهای موازی به ما کمک می‌کند تا لختی دورانی حول محور O را بر حسب محور C بیابیم. C محوری است که از مرکز جرمِ جسم عبور کرده است و O محوری است که می‌خواهیم لختی دورانی حول آن را محاسبه کنیم.

بنابراین فرض کنید که قصد داریم لختی دورانی جسمی را حول محور O که به فاصله d از محور C قرار گرفته، بدست آوریم. در این حالت رابطه زیر، بین این دو لختی دورانی برقرار است.

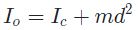
مثال 2

لختی دورانی دیسک زیر را حول محوری به فاصله r/3 از مرکز محاسبه کنید. فرض کنید لختی دورانی این جسم حول مرکز با استفاده از آزمایش اندازه‌گیری شده و برابر با I_C است (شکل زیر).

با توجه به قضیه محور‌های موازی می‌توان نوشت:

I_{حول مرکز}=I_c+md²

توجه داشته باشید که d فاصله از مرکز جسم است. بنابراین در این مثال برابر با r/3 در نظر گرفته می‌شود.

I_{حول مرکز}=I_c+m(r/3)²

I_{حول مرکز}=I_c+(mr²)/9

این قضیه در اشکال پیچیده کاربرد بسیاری دارد.

روش محاسبه لختی دورانی برخی اجسام پیوسته

لختی دورانی هر یک از اجسام پیوسته با توجه به محور مرجع مقدار متفاوتی دارد. در این قسمت لختی دورانی یک میله صلب یکنواخت را در حالتی که محور مرجع در مرکز و انتهای میله باشد، محاسبه می‌کنیم.

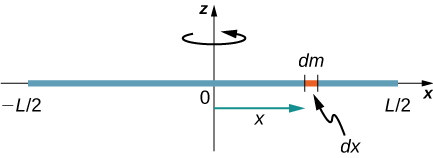
در شکل بالا محور میله در مرکز آن قرار گرفته است. برای محاسبه لختی دورانی این جسم از چگالی  خطی جرم یعنی $$\lambda$$ استفاده می‌کنیم. در این حالت $$\lambda=\frac{m}{l}$$ یا $$m=\lambda l$$ است. با گرفتن دیفرانسیل از دو طرف رابطه داریم:

$$dm=\lambda dx$$

حال اگر جزء طول را $$dx$$ و فاصله هر جزء جرم را تا محور، $$x$$ در نظر بگیریم با استفاده از رابطه لختی دورانی اجسام پیوسته داریم:

$$I=\int r^2 dm=\int x^2 dm=\int x^2 \lambda dx$$

با توجه به اینکه محور در مرکز میله قرار دارد پس حد انتگرال گیری بین $$-\frac{L}{2}$$ تا $$\frac{L}{2}$$ است. در نتیجه داریم:

$$\begin{aligned} I &=\int_{-L / 2}^{L / 2} x^{2} \lambda d x=\left.\lambda \frac{x^{3}}{3}\right|_{-L / 2} ^{L / 2}=\lambda\left(\frac{1}{3}\right)\left[\left(\frac{L}{2}\right)^{3}+\left(\frac{L}{2}\right)^{3}\right] \\ &=\lambda\left(\frac{1}{3}\right) \frac{L^{3}}{8}(2)=\frac{M}{L}\left(\frac{1}{3}\right) \frac{L^{3}}{8}(2)=\frac{1}{12} M L^{2} \end{aligned} 0$$

همین حالت برای زمانی که محور مانند شکل زیر در ابتدای میله است، به صورت زیر تغییر می‌کند:

$$\begin{aligned} I &=\int_{0}^{L} x^{2} \lambda d x=\left.\lambda \frac{x^{3}}{3}\right|_{0} ^{L}=\lambda\left(\frac{1}{3}\right)\left[(L)^{3}-(0)^{3}\right] \\ &=\lambda\left(\frac{1}{3}\right) L^{3}=\frac{M}{L}\left(\frac{1}{3}\right) L^{3}=\frac{1}{3} M L^{2} \end{aligned}$$

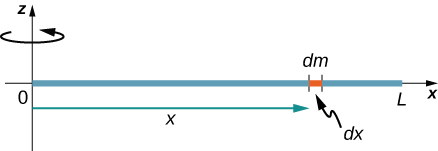
همان طور که می‌بینید محل محور در مقدار نهایی لختی دورانی جسم موثر است.

^^