اعداد رادیکالی و محاسبات مربوط به آن ها — به زبان ساده (+ دانلود فیلم آموزش گام به گام)
اغلب با مجموعه اعداد صحیح و طبیعی آشنایی دارید. انجام محاسبات برای این گونه اعداد به وسیله محور اعداد به راحتی میسر است. ولی اگر به مجموعه اعداد صحیح، اعداد رادیکالی را نیز اضافه کنیم، مجموعه اعداد ما ارتقاء یافته است و باید شیوه انجام محاسبات ریاضی را برای این اعداد نیز فراگیریم.
در این نوشتار از مجله فرادرس ابتدا اعداد رادیکالی را معرفی، سپس محاسبات ریاضی مانند جمع، تفریق، ضرب و تقسیم اعداد رادیکالی را یادآوری میکنیم. یکی از انواع اعداد رادیکالی، ریشه دوم یا جذر یک عدد است. به منظور آشنایی بیشتر با مفهوم ریشه دوم و نمایش آن روی محور اعداد بهتر است مطلب جذر یا محاسبه ریشه دوم عدد — به زبان ساده از مجله فرادرس را مطالعه کنید. همچنین خواندن نوشتار معادله رادیکالی — به زبان ساده نیز خالی از لطف نیست.
اعداد رادیکالی و محاسبات مربوط به آنها
به توان رساندن را به نوعی، ضرب کردن برای اعداد صحیح در نظر میگیریم. به این معنی که اگر a و b دو عدد صحیح و مثبت باشند، a به توان b را به صورت ضرب a به تعداد b بار در خودش در نظر میگیریم.
این رابطه در زیر نوشته شده است.
$$\large a^b = \underbrace{a\times a \times a \cdots\times a}_{b} =c$$
حال اگر این عمل را عکس کنیم چه اتفاقی میافتد. به این معنی که به دنبال عددی مثل a میگردیم که اگر آن را b با در خودش ضرب کنیم برابر با c شود. پیدا کردن این عدد بوسیله محاسبه رادیکال برمبنای b از عدد c حاصل میشود. رادیکال را در ریاضیات با علامت $$\sqrt{\;\;}$$ نشان میدهند. در این حالت مینویسیم.
$$\large \sqrt[b]{c}=a\rightarrow a^b =c$$
عبارت سمت چپ را به صورت «ریشه bام عدد c برابر است با a» میخوانند.
برای مثال اگر a=5 و b=3 باشد مقدار c نیز برابر با ۱۲۵ خواهد بود. در این حالت داریم:
$$\large \sqrt[3]{125}=5 \rightarrow 5^3 =125$$
عبارت سمت چپ به صورت «ریشه سوم ۱۲۵ برابر است با ۵» خوانده میشود.
نکته: اگر مقدار b برابر با ۲ باشد، a را ریشه دوم عدد c میگویند و مینویسند:
$$\large \sqrt{c} =a \rightarrow a^2 =c$$
در این حالت عبارت سمت چپ را به صورت «ریشه (یا رادیکال) c برابر است با a» میخوانند. همانطور که دیده میشود، برای ریشه دوم، دیگر از عدد ۲ در بالای رادیکال استفاده نمیکنند. پس متوجه میشویم هرگاه بالای رادیکال عددی دیده نشود، منظور ریشه دوم است. ریشه دوم را برای راحتی گاهی رادیکال نیز میخوانند.
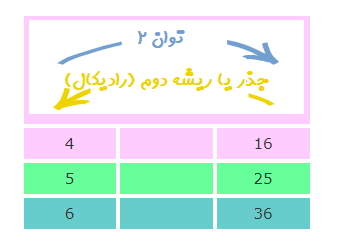
با توجه به اعداد و ارقامی که در جدول بالا دیده میشود، مشخص است که ریشه دوم یا رادیکال برای اعداد مثبت تعریف شده است. زیرا نمیتوان یک عدد صحیح را در خودش ضرب کرد و حاصل مقدار منفی بدست آید. بنابراین قادر به محاسبه $$\sqrt{(-4)}$$ یا $$\sqrt{-(25)}$$ نیستیم.
نکته: برای اعداد منفی، ریشههای زوج موجود نیست. ولی ریشههای فرد اعداد منفی وجود دارد. برای مثال:
$$\large \sqrt[\;3]{-125}=-5$$
زیرا:
$$(-5)\times (-5)\times (-5)=-125$$.
از آنجایی که توان ۲ یا مربع و رادیکال عکس یکدیگر هستند، بهتر است که به شکل تابع $$y=x^2$$ نیز نگاهی بکنیم.

اگر ریشه دوم را به صورت عکس تابع توان ۲ یا مربع در نظر بگیریم، شکل تابع رادیکال یا ریشه دوم با جابجا کردن محور افقی و عمودی یا چرخش ۹۰ درجهای نمودار قبلی بدست میآید.
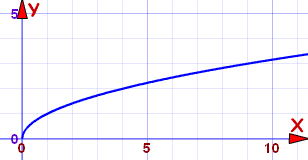
از آنجایی که ریشه دوم در بحث ما فقط برای اعداد نامنفی تعریف شده، این منحنی در نقطه 0 بریده شده است و دیگر ادامه نخواهد داشت.
نمایش اعداد رادیکالی به صورت توان
با توجه به رابطه عکسی که بین رادیکال و توان وجود دارد، به نظر میرسد که اگر $$a=\sqrt{c}$$ باید بتوان نتیجه زیر را نوشت:
$$\large \sqrt{c} = a \rightarrow a^2= a \times a = \sqrt{c} \times \sqrt{c}=c$$
به این ترتیب مشخص است که اگر رادیکال یک عدد را دوبار در خودش ضرب کنیم، با خود عدد برابر خواهد شد. این رابطه را میتوان به صورت توان نیز نوشت:
$$\large c^? \times c^? =c^1$$
از آنجایی که علامت ?ها یکسان هستند، هنگام ضرب دو عدد، توانها با هم جمع میشوند. بنابراین باید رابطه زیر برقرار باشد.
$$\large c^? \times c^? =c^{?+?} =c^1 \rightarrow 2\times ?=1 \rightarrow ?=\frac{1}{2}$$
در نتیجه میتوان ریشه دوم را به صورت توان $$\frac{1}{2}$$ نیز نشان داد. بنابراین خواهیم داشت:
$$\large \sqrt{c}=c^{\tfrac{1}{2}}$$
همین عمل را برای ریشههای سوم، چهارم و ... نیز میتوان انجام داد. در نتیجه تساوی زیر همیشه برقرار است.
$$\large \sqrt[3]{c} = c^{\tfrac{1}{3}}, \;\; \sqrt[4]{c}=c^{\tfrac{1}{4}},\;\; \sqrt[5]{c}=c^{\tfrac{1}{5}}, \cdots $$
نکته: اگر ارتباط بین a, b, c و d به صورت $$a^b = c^d$$ باشد، میتوان نوشت:
$$\large a= \sqrt[^b\;]{c^d} = c^{\tfrac{d}{b}}$$
برای مثال اگر a=4 , b= 2 ,c=2, d= 4 باشد داریم:
$$\large \sqrt[^2\;]{{2^4}} = 2^{\tfrac{4}{2}}=2^2=4$$
جمع، تفریق، ضرب و تقسیم اعداد رادیکالی
با توجه به شیوه نمایش توانی اعداد رادیکالی، براساس قواعد مربوط به اعداد تواندار میتوان عمل جمع، تفریق، ضرب و تقسیم را انجام داد. همانطور که میدانید هنگام جمع یا تفریق، اعداد با توانهای یکسان با یکدیگر به کار میروند.
در اینجا قواعد محاسباتی برای جملات تواندار را به اختصار معرفی میکنیم.
قاعده جمع و تفریق: هنگام جمع یا تفریق جملات تواندار، فقط ضرایب جملات با پایه و توانهای یکسان با یکدیگر جمع یا تفریق میشوند.
$$\large 2a^2+3b^3-5a^2-2b^3=-3a^2+b^3$$
قاعده ضرب و تقسیم: در ضرب جملات تواندار، توانهای جملاتی که دارای پایههای یکسان هستند با یکدیگر جمع میشوند. در تقسیم جملات تواندار نیز توانهای جملات با پایههای یکسان، از یکدیگر تفریق خواهند شد.
$$\large \dfrac{(3a^2 \times 4a^3 \times 5b^6)}{6b^4}= 10a^5b^2$$
مثال ۱
برای انجام محاسبات زیر میتوان از قواعد توان استفاده کرد. یعنی جملات با ریشههای یکسان با یکدیگر جمع یا تفریق میشوند.
$$\large \sqrt{2} + 5\sqrt[3]{8} - 3\sqrt{2} - 2\sqrt[3]{8}=-2\sqrt{2}+3\sqrt[3]{8}=-2\sqrt{2}+3\times 2 = 6-2\sqrt{2}$$
مثال ۲
رابطههای زیر را براساس قواعد ضرب برای جملههای تواندار، ساده میکنیم.
$$\large \sqrt{2 \times 3} = (2\times 3)^{\tfrac{1}{2}}=2^{\tfrac{1}{2}}\times 3^{\tfrac{1}{2}}=\sqrt{2} \times \sqrt{3}. $$
$$\large \sqrt{2}\times \sqrt[3]{2} = 2^{\tfrac{1}{2}} \times 2^{\tfrac{1}{3}} = 2^{(\tfrac{1}{2}+\tfrac{1}{3})}= 2^{(\tfrac{5}{6})}=\sqrt[^6\;]{2^5}.$$
مثال 3
براساس تبدیل رادیکال به توان، عبارتهای زیر را سادهتر مینویسیم.
$$\large \sqrt[^3\;]{2^4}=2^{\tfrac{4}{3}}=2^{(1+\tfrac{1}{3})}=2\times 2^{\tfrac{1}{3}}=2\sqrt[3]{2}.$$
$$\large \dfrac{\sqrt[^3\;]{2}}{\sqrt[^3\;]{3}}=\sqrt[^3\;]{\tfrac{2}{3}}.$$
مثال 4
براساس تبدیل رادیکال به توان عبارت زیر را ساده میکنیم.
$$\large \dfrac{\sqrt[^3\;]{2^4}\times \sqrt[^2\;\;]{4^3}}{\sqrt[^3\;]{8^4}}=\dfrac{2^{\tfrac{4}{3}}\times 4^{\tfrac{3}{2}}}{8^{\tfrac{4}{3}}}=\\ \large (\dfrac{2}{8})^{\tfrac{4}{3}}\times 4^{\tfrac{3}{2}}=(\dfrac{1}{4})^{\tfrac{4}{3}}\times (2^2)^{\tfrac{3}{2}}=\dfrac{1}{4^{(\tfrac{4}{3})}}2^{(\tfrac{6}{2})}= \\ \large \dfrac{2^3}{4\times 4^{(\tfrac{1}{3})}}=\dfrac{2^3}{4\times \sqrt[3]{4}}=\dfrac{2}{\sqrt[3]{4}}=\\ \large 2\times 4^({-\tfrac{1}{3}})=2\times 2^{(-\frac{2}{3})}=2^{(1-\tfrac{2}{3})}=2^{\tfrac{1}{3}}$$
از آنجایی که تمایل داریم که مخرج کسرها به صورت گویا نوشته شوند، خط آخر را در ادامه محاسباتمان اضافه کردهایم.
مثال 5
رابطه زیر را براساس قواعد ضرب و تقسیم برای جملههای تواندار، ساده میکنیم.
$$\large \dfrac{2\sqrt{2}\times 3\sqrt[5]{3}\times 5 \sqrt[3]{4}}{5\times \sqrt[3]{8}\times 10 \times \sqrt[5]{5}}=\dfrac{6}{10}\dfrac{2^{\tfrac{1}{2}}\times 3^{\tfrac{1}{5}}\times 4^{\tfrac{1}{3}}}{8^{\tfrac{1}{3}}\times 5^{\tfrac{1}{5}}}=\dfrac{3}{5}(2)^{\tfrac{1}{2}}\times (\dfrac{3}{5})^{\tfrac{1}{5}}\times (\dfrac{4}{8})^{\tfrac{1}{3}}=\\ \large
\dfrac{3}{5}(2)^{\tfrac{1}{2}}\times (\dfrac{3}{5})^{\tfrac{1}{5}}\times (\dfrac{1}{2^{\tfrac{1}{3}}})=\dfrac{3}{5}(\dfrac{3}{5})^{\tfrac{1}{5}}\times \dfrac{2^{\tfrac{1}{2}}}{2^{\tfrac{1}{3}}}=(\dfrac{3}{5})^{(1+\frac{1}{5})}\times 2^{ (\frac{1}{2}-\frac{1}{3})}=\\ \large (\dfrac{3}{5})^{(\frac{6}{5})}\times 2^{ (\frac{1}{6})}= \sqrt[^5\;]{(\tfrac{3}{5}})^6 \times \sqrt[6]{2}= \dfrac{3}{5}\sqrt[^5\;]{(\tfrac{3}{5}}) \times \sqrt[6]{2}=\\ \large \dfrac{3}{5}\sqrt[^5\;]\frac{3\times 5^4}{5\times 5^4}\times \sqrt[6]{2}=\dfrac{3}{25}\sqrt[^5\;]{3\times 5^4}\times\sqrt[6]{2}$$
از آنجایی که تمایل داریم که مخرج کسرها به صورت گویا نوشته شوند، خط آخر را در ادامه محاسباتمان اضافه کردهایم.
ریشه زوج اعداد
فرض کنید رابطه $$a^2=c$$ برقرار است. در نتیجه میتوان با گرفتن ریشه دوم از دو طرف این معادله را برحسب c حل کرد. بنابراین خواهیم داشت:
$$\large a^2=c \rightarrow a=\pm \sqrt{c},$$
زیرا با ضرب $$-\sqrt{c}$$ در خودش به a خواهیم رسید. همچنین $$\sqrt{c}\times \sqrt{c}= a $$.
آزمون اعداد رادیکالی
در این قسمت به منظور درک بهتر اعداد رادیکالی و محاسبات مربوط به آنها، تعدادی پرسش چهار گزینهای به صورت آزمون تهیه شده است.
حاصل $$\sqrt[3]{ - 512 } $$ برابر است با:
۲-
۸-
۱۶-
۸+
برای محاسبه $$\sqrt[3]{ - 512 } $$، ابتدا عدد زیر رادیکال را به عوامل اول ان تجزیه میکنیم:
$$512 = 2 ^ 9 $$
بنابراین، عبارت رادیکالی داده شده را میتوانیم به صورت زیر بنویسیم:
$$ \sqrt[3]{ - 2 ^ 9 } $$
به این نکته توجه داشته باشید که اعداد مثبت و منفی میتوانند زیر رادیکال با فرجه فرد قرار بگیرند، اما تنها اعداد مثبت و صفر را میتوانیم زیر رادیکال با فرجه زوج قرار دهیم. در این مسئله فرجه رادیکال برابر سه است، بنابراین عدد ۵۱۲- میتواند زیر آن قرار داشته باشد:
$$ \sqrt[3]{ - 2 ^ 9 } \\ ( - 2 ^ 9 ) ^ { \frac { 1 } { 3 } } = ( -2) ^ 3 = -8 $$
حاصل عبارت $$\sqrt[3]{ - 1000 } $ برابر است با:
۱۰۰
۱۰
۱۰۰-
۱۰-
برای محاسبه $$\sqrt[3]{ - 1000 } $$، ابتدا عدد زیر رادیکال را به عوامل اول ان تجزیه میکنیم:
$$1000 = 2 ^ 3 \times 5 ^ 3 $$
بنابراین، عبارت رادیکالی داده شده را میتوانیم به صورت زیر بنویسیم:
$$ \sqrt[3]{ - 2 ^ 3 \times 5 ^ 3 } $$
به این نکته توجه داشته باشید که اعداد مثبت و منفی میتوانند زیر رادیکال با فرجه فرد قرار بگیرند، اما تنها اعداد مثبت و صفر را میتوانیم زیر رادیکال با فرجه زوج قرار دهیم. در این مسئله فرجه رادیکال برابر سه است، بنابراین عدد ۱۰۰۰- میتواند زیر آن قرار داشته باشد:
$$ \sqrt[3]{ - 2 ^ 3 \times 5 ^ 3 } \\ ( - 2 ^ 3 \times 5 ^ 3 ) ^ { \frac { 1 } { 3 } } = -10 $$
حاصل عبارت $$\sqrt { 8 y ^ 3 } $$ برابر است با:
$$ 2y \sqrt { 2 y } $$
$$ 2y \sqrt { y } $$
$$ y \sqrt { 2 y } $$
$$ \sqrt { 2 y } $$
عبارت زیر رادیکال را به صورت زیر مینویسیم:
$$ 8 y ^ 3 = ( 4 y ^ 2 ) ( 2 y ) $$
در نتیجه، حاصل عبارت $$\sqrt { 8 y ^ 3 } $$ برابر است با:
$$\sqrt { 8 y ^ 3 } = \sqrt { ( 4 y ^ 2 ) ( 2 y ) } = \sqrt { 4 y ^ 2 } \sqrt { 2 y } = 2y \sqrt { 2 y } $$
با فرض آنکه $$x$$ و $$y $$ و $$ z $$ مثبت هستند، ساده شده عبارت $$\sqrt [ 3 ] { 54 x ^ 6 y ^ 7 z ^ 2 } $$ برابر است با:
$$3 x ^ 2 y ^ 2 \sqrt [ 3 ] { 4 y z ^ 2 } $$
$$3 x ^ 2 y ^ 2 \sqrt [ 3 ] { y z ^ 2 } 2 $$
$$3 x ^ 2 y ^ 2 \sqrt [ 3 ] { 2 y z ^ 2 } $$
$$3 x y \sqrt [ 3 ] { 4 y z ^ 2 } $$
برای ساده کردن $$\sqrt [ 3 ] { 54 x ^ 6 y ^ 7 z ^ 2 } $$، عبارت زیر رادیکال را به صورت زیر مینویسیم:
$$ 54 x ^ 6 y ^ 7 z ^ 2 = ( 27 x ^ 6 y ^ 6 ) ( 2 y ^ 1 z ^ 2 ) = 3 ^ 3 ( x ^ 2) ^ 3 ( y ^ 2 ) ^ 3 ( 2 y z ^ 2 ) $$
با توجه به بازنویسی عبارت زیر رادیکال داده شده به صورت فوق، داریم:
$$\sqrt [ 3 ] { 54 x ^ 6 y ^ 7 z ^ 2 } = \sqrt [ 3 ] { 3 ^ 3 ( x ^ 2) ^ 3 ( y ^ 2 ) ^ 3 ( 2 y z ^ 2 ) } = \sqrt [ 3 ] { 3 ^ 3 ( x ^ 2 ) ^ 3 ( y ^ 2 ) ^ 3 } \sqrt [ 3 ] { 2 y z ^ 2 } = 3 x ^ 2 y ^ 2 \sqrt [ 3 ] { 2 y z ^ 2 } $$
در صورتی که $$x $$ و $$y $$ و $$z $$ مثبت باشند، حاصل عبارت $$\sqrt [ 4 ] { 4 x ^ 3 } y \sqrt [ 4 ] { 8 x ^ 2 y ^ 3 z ^ 5 } $$ برابر است با:
$$ xyz \sqrt [ 4 ] { 2 x z } $$
$$2 xyz \sqrt [ 4 ] { x z } $$
$$2 xyz \sqrt [ 4 ] { 2 z } $$
$$2 xyz \sqrt [ 4 ] { 2 x z }$$
هنگامیکه دو رادیکال با فرجههای یکسان با یکدیگر ضرب میشوند، ابتدا آنها را به صورت یک رادیکال مینویسیم. از اینرو، عبارت $$\sqrt [ 4 ] { 4 x ^ 3 } y \sqrt [ 4 ] { 8 x ^ 2 y ^ 3 z ^ 5 } $$ را میتوانیم به صورت زیر بنویسیم:
$$ $$\sqrt [ 4 ] { 4 x ^ 3 } y \sqrt [ 4 ] { 8 x ^ 2 y ^ 3 z ^ 5 } $$ = \sqrt [ 4 ] { ( 4 x^ 3 y ) ( 8 x ^ 2 y ^ 3 z ^ 5 ) } = \sqrt [ 4 ] { 32 x ^ 5 y ^ 4 z ^ 5 }$$
عبارت $$32 x ^ 5 y ^ 4 z ^ 5 $$ را به صورت زیر مینویسیم تا به راحتی بتوانیم قسمتی از آن را از زیر رادیکال خارج کنیم:
$$ 32 x ^ 5 y ^ 4 z ^ 5 = ( 2 ^ 4 x ^ 4 y ^ 4 z ^ 4 ) ( 2 x z ) $$
در نتیجه، عبارت $$\sqrt [ 4 ] { 4 x ^ 3 } y \sqrt [ 4 ] { 8 x ^ 2 y ^ 3 z ^ 5 } $$ به صورت زیر ساده میشود:
$$\sqrt [ 4 ] { 4 x ^ 3 } y \sqrt [ 4 ] { 8 x ^ 2 y ^ 3 z ^ 5 } = \sqrt [ n ] { 32 x ^ 5 y ^ 4 z ^ 5} = \sqrt [ 4 ] 2 ^ 4 x ^ 4 y ^ 4 z ^ 4 \sqrt [ 4 ] { 2 x z } = 2 xyz \sqrt [ 4 ] { 2 x z } $$
اگر p و q اعداد مثبتی باشند، ساده شده عبارت زیر برابر است با:
$$\frac { \sqrt [ 3 ] { q } \times 3 \sqrt [ 3 ] { q ^ 2 } \times 2 \sqrt { p }} { 2 \times\sqrt { q ^ 2 } \times \sqrt [ 3 ] { q ^ 4 } } $$
$$\frac { 3 \sqrt { p } \times \sqrt [ 3 ] { q ^ 2 }} { q ^ 2 } $$
$$\frac { 3 \sqrt { p } \times \sqrt [ 3 ] { q ^ 2 }} { q } $$
$$\frac { \sqrt { p } \times \sqrt [ 3 ] { q ^ 2 }} { q ^ 2 } $$
$$\frac { 3 \sqrt { p } \times \sqrt [ 3 ] { q }} { q } $$
عبارت داده شده را به صورت زیر ساده میکنیم:
$$\frac { \sqrt [ 3 ] { q } \times 3 \sqrt [ 3 ] { q ^ 2 } \times 2 \sqrt { p }} { 2 \times\sqrt { q ^ 2 } \times \sqrt [ 3 ] { q ^ 4 } } = \frac { 3 \sqrt [3 ] { q \times q ^ 2 } \times 2 \sqrt { p } } { 2 \sqrt { q ^ 2 } \times \sqrt[ 3 ] { q ^ 3 \times q }} \\ = \frac { 3 \sqrt [ 3 ] { q ^ 3 } \times 2 \sqrt { p } } { 2 \sqrt { q ^ 2 } \times \sqrt [ 3 ] { q ^ 3 \times q }} \\ = \frac { 3 q \times 2 \sqrt { p } } { 2 q \times q \sqrt [ 3 ] { q } }= \frac { 2 q \times 3 \sqrt { p } }{ 2 q \times q \sqrt [ 3 ] { q }} \\ = \frac { 3 \sqrt { p } } { q \sqrt [3 ] { q } } \times \frac { \sqrt [ 3 ] { q ^ 2 }} { \sqrt [ 3 ] { q ^ 2 } } = \frac { 3 \sqrt { p } \times \sqrt [ 3 ] { q ^ 2 }} { q ^ 2 } $$











برای حل اعدادی که پایه انها عدد صحیح است و توان آن رادیکالی باشد رو از کجا بدست بیاریم مثل دو به توان رادیکال ۵
سلام و وقت بخیر؛
از آنجایی که اعداد رادیکالی، عضو مجموعه اعداد گنگ هستند، نمیتوان با بیان آنها به صورت کسری، مثال مورد نظر شما را به راحتی به دست آورد. زیرا خود عدد 2 به توان رادیکال 5 (یا هر عدد تواندار دیگر با توان رادیکالی)، یک عدد گنگ محسوب میشود. بنابراین، دو راه وجود خواهد داشت: ۱) بیان عدد به همان صورتی که هست (2 به توان رادیکال 5). البته اگر امکان سادهسازی عبارت درون رادیکال و بیرون کشیدن یک عدد صحیح از آن وجود داشته باشد، میتوان برای سادهسازی بیشتر، این کار را انجام داد. ۲) استفاده از تقریب. در این روش، میگوییم رادیکال 5، تقریبا برابر است با 2/24. پس، 2 به توان رادیکال 5، تقریبا برابر است با 2 به توان 2/24. اکنون میتوانیم 2/24 (یک عدد گویا) را به صورت کسری بنویسیم و با توجه به روشهای موجود، جواب تقریبی 2 به توان رادیکال 5 را به دست بیاوریم.
از همراهی شما با مجله فرادرس سپاسگزاریم.
سلام ببخشید منظور این سوال چیه ؟
اگر x<0 مقدار x برحسب رادیکال منفی ایکس را بنویسید.
سلام اگه ۳ زیر دو تا √ باشه جواب چی میشه لطفاً توضیح بدید (√..منظورم رادیکاله)
رادیکال اول میشه سه به توان یک دومم ورابوکال دوم میشه سه به توان یک دومم ضرب یک دومم.
سلام وقت بخیر
حاصل عبارت منفی ۲ × رادیکال ۲ به توان یکسوم چه میشود؟
سلام لطفا بگين جواب (٨٠٠)به توان٢ +(٨٠٠) به توان٢ هردو زير راديكال فرجه دو چى ميشه
سایتتون فوق العاده هس چیزی کم نداره ممنون ازتون
سلام وقت بخیر.
اگه بخوایم ۴ رادیکال ۱۰ رو تقسیم بر ۲ کنیم باید چکار کنیم؟
سلام . اینو چجوری حل کنم؟ ²(2-3)+²(1-1)√=x
سلام وقت بخیر ایا اگر بخواهیم دو طرف یک نامعادله رادیکالی را به توان 2 برسانیم باید پس از به توان رساندن انها را در قدر مطلق قرار دهیم ؟
عالی بود
اره ولی خب اگه قدر مطلقش برابر با خودش نباشه که یعنی عبارت زیر رادیکال منفی بوده و کلا صورت سوال غلط میشه
با سلام؛
برای حل یک نامعادله رادیکالی ابتدا دامنه هر یک از عبارتهای رادیکالی را با قرار دادن عبارت زیر رادیکال، بزرگتر و مساوی صفر، بهدست میآوریم. سپس، طرفین نامعادله را به توان دو میرسانیم و آن را حل میکنیم. در پایان، جواب نهایی برابر اشتراک دامنه رادیکالها و جواب نامعادله است.
با تشکر از همراهی شما با مجله فرادرس
سلام یک دنیا سپاس عالی بودید و هستید و خواهید بود
رادیکال7x+رادیکال7y- رادیکال7 به توان۳zجوابش میشه بگید
سلام چگونه میشه از یک تساوی زیر لگاریتم گرفت 5^13√*20^98√*13^G=√99فرجه تمامی رادیکال ها50 میباشد
سلام ببخشید منفی یک بر روی رادیکال دو منها منهای رادیکال دو چند میشه
منفی یک میشه چون مثبت رادیکال ۲ومنفی رادیکال ۲ علامت هاشون قرینه هست
تشکر از زحمات شما
سلام ضرب یک عدد صحیح در رادیکال چطوریه؟
با سلام؛
خوشحالیم که مطالعه این مطلب برای شما مفید بوده است.
با تشکر از همراهی شما با مجله فرادرس
سلام
ببخشید چگونه رادیکالی که جذر مشخص ندارد را محاسبه کنیم ؟
مثلا رادیکال 4 می شود 2 .
رادیکال 21 چند میشود ؟؟
سلام.
به آموزش «جذر تقریبی و روش محاسبه آن — آموزش به زبان ساده و با مثال» مراجعه کنید.
سالم و سربلند باشید.
سلام ببخشید من اخیرن یه کلیپی توی نت دیدم که راحت ترین روش محاسبه رادیکال رو نشون میداد . اونم این روش بود که رقم های عدد زیر رادیکال رو جمع میکرد و منفی ریشه ی رادیکال میکردن
مثلا : رادیکال ۲۵ ( ریشه دوم ) : دو بعلاوه پنج مساوی میشود با ۷ و ۷ منفی ۲ میشود ۵ . ( جواب صحیح است ! )
مثال دوم : رادیکال ۳۴۳ ( ریشه سوم ) : سه بعلاوه چهار بعلاوه سه مساوی میشود با ۱۰ . ۱۰ منفی ۳ میشود ۷ ( جواب صحیح است ! )
مثال سوم : رادیکال ۱۲۵ ( ریشه دوم ) : ۱+۲+۵=۸ و ۸ منفی ۲ مساوی با ۵ ( جواب صحیح است )
اگر بزارید تا شب براتون کل رادیکال ها رو با این روش محاسبه میکنم . اگه امکانش هست این روش رو توی مقالتون قرار بدین که خیلی از ماها دنبالشیم
ببخشید ولی 8 منفی 2 نمیشه 5 میشه 6 جواب درست نیست
سلام و روز شما به خیر؛
روشی که معرفی کردید ممکن است برای برخی اعداد به صورت تصادفی درست به دست بیاید اما این روش عمومیت ندارد، برای مثال ریشه دوم عدد 81 با استفاده از روشی که شما بیان کردید برابر با 7 به دست میآید در حالی که 81 مجذور کامل عدد 9 است و حتی یک مثال نقض میتواند شمولیت یک حکم علمی را زیر سوال برد (هر چند این روش برای بسیاری از اعداد دیگر نیز جواب درست را به دست نمیدهد).
از اینکه با فرادرس همراه هستید خرسندیم.
6b^4/ (3a^2*4a^3*5b^6)
درود برشما
فکرکنم در حاصل مثال قاعده ضرب و تقسیم اشتباهی صورت گرفته باشه
سلام دوست عزیز،
در روال محاسبه صورت گرفته، ابتدا ضرایب را در هم ضرب و به ضریب مخرج تقسیم کردهایم. به همین جهت ضریب ۱۰ بوجود آمده است. توانهای جملات مشابه در ضرب نیز با یکدیگر جمع شدهاند که در نتیجه مقدار توان عبارت a برابر با ۵ خواهد بود. برای تقسیم عبارتهای با جمله b نیز توانها را از هم کم کردهایم. به این ترتیب نتیجه نوشته شده بدست خواهد آمد.
از همفکری و همیاری شما بسیار سپاسگزاریم.
تندرست و پیروز باشید.
سلام
خواهشا بگید چطوری این محاسبه انجام میشه :
????
رادیکال ۶۰ = ۲ رادیکال ۱۵ ؟؟؟؟؟
سلام وقت شما بخیر؛
از تجزیه ۶۰ کمک بگیرید. ۴ × ۱۵ = ۶۰ پس می توان جذر۶۰ را به کمک حاصل ضرب جذر ۱۵ × ۴ نوشت که چون جذر ۴ برابر با ۲ است نتیجه به صورت ۲ رادیکال ۱۵ درآمده
موفق باشید.
سلام چطور میشه یه عدد رادیکالی که ضریب داره رو روی محور نشون بدیم
مثلا ۲ رادیکال ۵
سلام و درود،
در متن جذر یا محاسبه ریشه دوم عدد — به زبان ساده، نحوه مشخص کردن اندازه رادیکال ۵ را آموختیم. حال کافی است دهانه پرگار را به این اندازه باز کنید و از محل نقطه ۲ روی محور اعداد، یک کمان بزنید تا محورها را قطع کند. محل برخورد این کمانها دو نقطه ۲ بعلاوه رادیکال ۵ و ۲ منهی رادیکال ۵ را نشان میدهد.
از اینکه سوالاتتان را با ما مطرح میکنید، سپاسگزاریم.
پیروز و سربلند باشید.
سلام
جواب شش منهای دو رادیکال پنج چند میشه؟
ببخشید میشه توضیح بدید وقتی 9x²√ هردو عدد زیر رادیکال چرا وقتی میاد بیرون در قدر مطلق قراره میگیره|۳x|به شرط اینکه x<0 هست؟چرا به شکل سه ایکس نمیاد بیرون؟ حتی اگر ایکس منفی باشه با به توان دو دیگه مثبت میشه
سلام
خب اول میایم جذر رادیکال 5 رو میگیریم ک حدودا میشه 2 و خورده ای، بعد 2 رو ضربدر 2 و خورده ای میکنیم ک ی عددی بین 5 تا 6 در میاد.
سپس 6 رو منهای عدد بدست آمده میکنیم و جواب بدست میاد، اگه قدر مطلق همین عبارت رو بخوایم بنویسیم خود اون عبارت رو مینویسیم چون جواب یک عدد مثبت میشه.
آیا رادیکال 78 چند است؟؟؟؟؟؟؟؟
بالاخره نفهمیدیمرادیکال ۱۶ میشود ۴ با مثبت منفی ۴
سلام ما را بپذیرید.
از آنجایی که مقدار رادیکال با فرجه زوج همیشه مثبت است رادیکال ۱۶ برابر با مثبت ۴ است. ولی اگر به حل معادله $$X^2 = 16$$ علاقمند هستید، دو جواب ۴ مثبت و منفی، پاسخ شما را میسازند.
پس همیشه ریشه های زوج را با مقدار مثبت نشان میدهیم ولی حل معادله درجه ۲ میتواند ریشه مثبت یا منفی داشته باشید.
پیروز و سربلند باشید.
سلام
چطور میشه دو رادیکال که زیر هم هستند رو حساب کرد؟
مثلا رادیکال رادیکال دو(فرجه هر دو رادیکال یکی باشه مثلا فرجه هر دو تا ۲ باشه)
سلام و وقت بخیر،
برای محاسبه رادیکال (رادیکال) کافی است که فرجهها را به صورت توان نوشته (مثلا رادیکال به صورت توان یک دوم نوشته میشود) و آنها را در یکدیگر ضرب کنید. برای مثال رادیکال رادیکال ۲ برابر است با ریشه چهارم ۲.
تندرست و پیروز باشید.
سلام ممنون واقعا عالی بود
یه سوال داشتم چجوری 2 رو به توان رادیکال 2 برسونم ؟
سلام
باید مقدار تقریبی رادیکال دو را بدست بیاوریم.مثلا اگر برای تمرین و محاسبات دم دستی بخواهید،تا یک رقم کافیست
اما مثلا اگر برای فعالیت های آزمایشگاهی بخواهیم،چون دقت بالاتر نیاز است ،باید تا سه رقم حساب کنیم.سپس کسر عدد اعشاری را بدست بیاوریم و طبق روشی که در بالا گفته شد،عدد به توان یک عدد کسری را حساب کنیم
خیلی خوب دمتون گرم خسته نباشید منتها من فقط یکم گیج شدم? راه حل ها یکم پیچیده ست.
اگه روشی هستش که مفهوم رادیکال و فرجه و… از این جور محاسبات رو بشه راحت تر یاد گرفت بگین خیلی ممنون تون میشم. با تشکر از سایت خوب تون?
چطور میشه رادیکال ۱۰ را حل کرد لطفا پاسخ بدید ممنون
چگونه باید باید عبارت های رادیکالی رو به ازای xتعریف نشده بنویسم ؟
x^2-6x+5√ این به چه صورت حساب میشه اگه قرار باشه به ازای x تعریف نشده باشد
دوست و همراه عزیز و گرامی، سلام؛
همانطور که میدانید، برای محاسبه رادیکال با فرجه زوج، باید زیر رادیکال، مثبت باشد. پس کافی است رابطه زیر رادیکال را تعیین علامت کنید. به منظور مشاهده روش تعیین علامت عبارتهای جبری و نامساویها اینجا کلیک کنید.
تندرست و پیروز باشید.
سلام بر همراه مجله فرادرس،
برای آشنایی با نحوه محاسبه ریشه دوم یا جذر گرفتن به مطلب جذر یا محاسبه ریشه دوم عدد — به زبان ساده مراجعه کنید. با سه روش، هندسی، نیوتن و تجزیه به عوامل اول، محاسبه ریشه یا جذر در آن متن آموزش داده شده است.
امیدوارم که پاسخ خود را در آنجا پیدا کنید.
موفق و تندرست باشید.
88 به توان 6
80 به توان 5
65 به توان 7
55 به توان 2
اینا درهم ضرب هستند و زیر رادیکال با فرجه 20
اینو چطور محاسبه کنم؟
آقا برای مثال رادیکال 10 از نقطه( A(1.2
میگذره یا نه اینو چجوری حساب کنیم؟
عالیییی
دوست عزیز، سلام:
سوال شما متاسفانه نامفهوم است. رادیکال ۱۰ یک عدد است و نقطه شما دو بعدی است. چگونه میتوان یک عدد را با یک نقطه تقاطع داد؟
مقدار رادیکال ۱۰ یک عدد حدود ۳ تا ۴ است. لطفا با دقت بیشتری سوال خود را مطرح کنید.
همراهی شما با مجله فرادرس، افتخار ما است.
ارادتمند،
آرمان ریبد
سلام.
اگر به نمودار $$y=\sqrt {x}$$ دقت کنید، میبینید که به ازای $$x=10$$، مقدار $$y$$ یا همان رادیکال ۱۰ عددی بین ۳ و ۳٫۵ خواهد بود. برای آشنایی با روش محاسبه جذر اعداد، پیشنهاد میکنیم به آموزش «جذر یا محاسبه ریشه دوم عدد — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.
از همراهیتان با مجله فرادرس خوشحالیم.
خدا خیرتون بده
چندین ساله داریم تو مدرسه برا خودمون درجا میزنیم
ور میداریم برا یه عبارت ساده پنجاه جور باز و بسته کردن و ساده کردن انجام میدیم…
یکی هم بهمون نمیگفت ساده تر هم میشه انجامش داد
مجموعه فرادرس کلا بی همتاست… اجرتان با ابا عبدالله
آیا 0/5 می تواند فرجه باشد ؟
عالی
سلام
عددی مثل نیم (0.5) رو در نظر بگیرید.
جذر این عدد چجوری بدست میاد؟
بطور کلی جذر اعداد بین 0تا 1 رو چجوری
روی کاغذ حساب کنیم؟
سلام.
برای آشنایی با روش محاسبه جذر یک عدد، پیشنهاد میکنیم مطلب «جذر یا محاسبه ریشه دوم عدد — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» را مطالعه کنید. برای جذر اعداد اعشاری، یک راه ساده از بین بردن اعشار آنها است. بدین صورت که مثلاً برای عدد ۰٫۵ آن را در ۱۰۰ ضرب کرده و جذر آن را محاسبه کنید. در نهایت، برای خنثی کردن تغییرات (ضرب ۰٫۵ در ۱۰۰)، جواب نهایی را بر ۱۰ تقسیم کنید (چون ۱۰۰ زیر رادیکال برابر با ۱۰ است).
سلام میشه بگین اولین عدد صحیح بزگتر از ۱۴√ + ۷ چه عددی هست
۱۱
رادیکال۱۴میشه ۳و خورده ای و بعلاوه هفت میشه ۱۰و خورده ای پس عدد صحیح بعد از اون میشه ۱۱
با عرض سلام و خسته نباشید به همه عزیزان .یه نفر میتونه به من بگه چطور جواب 2به توان رادیکال 2اگه زیر رادیکال بره میشه 2به توان رادیکال2/2 ام
سلام و وقت بخیر به همراه گرامی مجله فرادرس
همانطور که در در متن اعداد رادیکالی دیده میشود، میتوان ریشه دوم را به صورت توان معکوس نوشت، یعنی
$$\sqrt{2}=2^{1/2}$$. حال در نظر بگیرید که این عدد دوباره ریشه دوم بگیریم. با توجه به قانون ضرب توانها خواهیم داشت:
$$\sqrt{2^{\sqrt{2}}}=(2^{\sqrt{2}})^{1/2}=2^{(\sqrt{2}/2)}$$
از اینکه همراه مجله فرادرس هستید و مطالب آن را پیگیری میکنیم، بینهایت سپاسگزاریم.
موفق، سلامت و شاد باشید.
توضیحاتتون عالییییی بود و خیلییی به درد من خورد.
ازتون متشکرم و یک دنیا دعای خیر و آرزوهای خوب براتون میکنم.
سلام لطفا چگونگی محاسبه جذر اعداد با فرجه بیشتر از دو را بیشتر و واضح تر توضیح بدین به فرض مثال چگونگی محاسبه جذر ۴ با فرجه ۴ یا محاسبه دو رادیکال در رادیکال ۴ با فرجه ۲
سلام.باتشکر از نویسنده.آیا میشه که فورجه رادیکال منفی یا کسری هم باشه؟؟؟؟؟
با سلام و خسته نباشید به دوستان عزیز به خصوص نویسنده محترم. مطلب بسیار آموزنده ای بود.
در مورد مثال 4 امکان ساده تر شدن پاسخ به عبارت زیر وجود داره:
ریشه سوم 2 (2 به توان یک سوم)
ممنون
سلام
من یک سوال ساده دارم:
به ما گفتن که فرق ریشه و رادیکال اینه که در ریشه جواب هم مثبت هست و هم منفی. مثلا ریشه ۲۵ برابر مثبت منفی ۵ هست درحالی که رایکال x با فرجه ۲ برابر با قدر مطلق ریشه دوم اون هست یعنی فقط ۵
بعدش به ما گفتن که از دوطرف معادله میشه جزر گرفت ولی رادیکال نمیشه
حالا خواستم بدونم چزا نمیشه از دو طرف رادیکال گرفت؟
سلام و سپاس از همراهی شما با فرادرس.
همانطور که تذکر دادهاید، بهتر است کسرهای رادیکالی دارای مخرج گویا باشند. بنابراین متن مطابق با همین موضوع اصلاح شده است.
از اینکه خواننده مطالب فرادرس هستید متشکریم؛ منتظر پیامها و راهنماییهای بیشتر شما هستیم.
با سلام خدمت دوستان من یک سوال داشتم در مورد اعداد گنگ (اصم) اونم این هست
عدد 3-√10 بین کدوم دو عدد صحیح قرار دارد ؟ یا
(3منفی رادیکال 10 = بین دو کدام عدد صحیح است روش فهمیدن ان )
جوابش شده بین 0 و 1 چجوری این عدد بین 0 و 1 قرار دارد
با سلام و تشکر از اینکه همراه فرادرس هستید…
واضح است که ریشه دوم ۱۰ بین دو عدد ۳ و ۴ قرار دارد. زیرا مربع ۳ برابر با ۹ و مربع ۴ نیز ۱۶ است در نتیجه بازه یا فاصله بین ۳ و ۴ مقدار ریشه دوم ۱۰ را در بر میگیرند. پس یک نامساوی به صورت زیر داریم:
$$3
سلام ببخشید چرا جواب رادیکال2+3 و رادیکال2_3 میشه رادیکال2+1؟ چجوری جساب کرده؟
سلام
نکته خوب مقاله اینه که با زبان ساده توضیح داده شده .فهمش آسونتره.مرسی
سلام
در قاعده ضرب وتقسیم جواب مثال اشتباه است
واقعا فاجعه بود ، چند تا مثال با اعداد ساده میزاشتین ادم متوجه بشه از یه جایی به بعد گنگش کردین
سلام
یه سوال داشتم
که آیا ممکنه یک عدد به توان دو برسه و جواب اون منفی یک بشه
ممنون
نه هیچوقت
نه نمیشه چون یه عدد ضرب در خودش میشه یا مثبت ضربدر مثبته یا منفی ضربدر منفی و مثبت ضربدر مثب میشه مثبت و منفی هم ضربدر منفی میشه مثبت پس عدیی وجود نداره که به توان 2 برسه و منفی بشه حالا هر عدد منفی ای باشه
با سلام و درود خدمت شما خواننده گرامی
از اینکه همراه فرادرس هستید بسیار خرسندیم… در مورد سوال شما باید گفت که هیچ عدد حقیقی وجود ندارد که به توان ۲ رسیده و منفی شود. ولی اگر محیط و فضای اعداد را به اعداد مختلط گسترش دهیم، میتوان گفت که i=$$\sqrt{-1}$$ عددی است که توان ۲ آن برابر است با ۱-. بنابراین پاسخ شما در مجموعه اعداد مختلط وجود دارد.
باز هم از اینکه به نوشتارهای وبلاگ فرادرس توجه دارید سپاسگزاریم.