ویسکوزیته (Viscosity) — به زبان ساده

ویسکوزیته، لزجت یا گرانروی یک سیال (مایع یا گاز)، پارامتری است که میزان مقاومت آن را در مقابل جاری شدن نشان میدهد. این پارامتر، یکی از مهمترین پارامترهایی است که خواص سیال را بیان میکند و از آن در اکثر مسائل مکانیک سیالات استفاده میشود. ویسکوزیته را میتوان در تحلیل ابعادی برای محاسبه اعداد بیبعد مختلفی مانند عدد رینولدز استفاده کرد، همچنین این مفهوم، کاربرد بسیار زیادی در تحلیل میدان جریان به کمک معادلات ناویر-استوکس در علم دینامیک سیالات محاسباتی نیز دارد. بنابراین میتوان ویسکوزیته را یکی از پایهایترین مفاهیم مکانیک سیالات دانست.
در این مطلب از مجله فرادرس، ابتدا به بررسی مفهوم ویسکوزیته و روابط حاکم بر ویسکوزیته سینماتیک و ویسکوزیته دینامیک پرداخته میشود. در ادامه، شیوه اندازهگیری این پارامتر و عوامل موثر در ویسکوزیته مایعات و گازها مورد بحث قرار میگیرند. همچنین تفاوت میان ویسکوزیته سیالات نیوتنی و غیر نیوتنی به صورت مختصر بیان میشود. در انتها نیز روابطی برای تخمین ویسکوزیته سیالاتی با ویسکوزیته نامعین، معرفی میشوند.
ویسکوزیته چیست؟
همانطور که اشاره شد، ویسکوزیته یا لزجت یک سیال (مایع یا گاز)، میزان مقاومت آن را در مقابل جاری شدن بیان میکند. زمانی که جسمی درون یک سیال به حرکت در میآید، سیال اطراف این جسم، در مقابل حرکت مقاومت نشان میدهد به طوری که سرعت لایههای مختلف سیال اطراف این جسم، متفاوت است.
رفتار سیال در یک جریان به دو مشخصه ذاتی آن، یعنی «چگالی» (Density) و «ویسکوزیته» (Viscosity) بستگی دارد. برای مثال زمانی که جسم جامدی از درون یک سیال عبور میکند باید با نیروی مقاومت سیال مقابله کند. این مقاومت به سرعت نسبی بین سیال و جامد، شکل جامد، چگالی سیال و ویسکوزته آن بستگی دارد. مثال دیگر این است که توان لازم برای عبور سیال از درون یک مجرا به سرعت سیال، قطر مجرا، چگالی سیال و ویسکوزیته آن بستگی دارد.
برای اثبات وجود این پدیده، فرایندی را در نظر بگیرید که در آن، دو صفحه موازی و افقی در یک سیال با فاصله بسیار کم Y قرار داده شدهاند. در این حالت، اگر صفحه بالا ساکن باقی بماند و صفحه پایین با سرعت u0 حرکت کند، لایهای از سیال که در نزدیکی صفحه پایینی قرار دارند شروع به حرکت میکند و حرکت این لایه به تدریج باعث حرکت لایههای بالایی سیال نیز میشود.
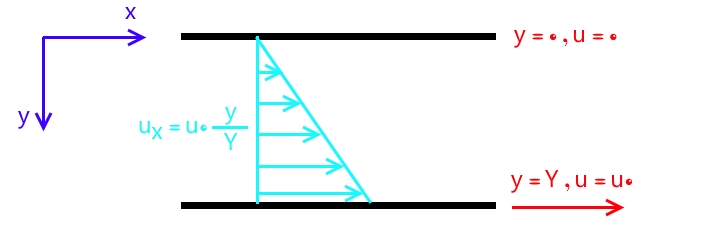
مطابق شکل، در حالتی که جریان به حالت پایا میرسد، سرعت لایه بالای سیال که در نزدیکی صفحه ساکن قرار دارد، همچنان برابر با صفر است ولی لایه پایینی سیال که در تماس با صفحه متحرک قرار دارد، با سرعت u0 حرکت میکند. در این حالت، اگر توزیع سرعت در لایههای میانی سیال را اندازهگیری کنیم، متوجه خواهیم شد که سرعت به صورت خطی با فاصله y از صفحه ساکن تغییر میکند. رابطه این سرعت را میتوان به شکل زیر نمایش داد.
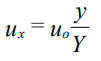
همانطور که مشاهده میشود، زمانی که در لایهای از سیال با ارتفاع y=۰ قرار داریم، سرعت سیال برابر با سرعت صفحه بالایی و صفر است ولی زمانی که در مجاورت صفحه پایین یعنی y=Y قرار داریم، سرعت سیال برابر با سرعت صفحه پایین یعنی u0 است.
در این شرایط، فرض کنید که نیروی افقی برابر با Fx- است که در خلاف جهت سرعت u0 اعمال میشود و صفحه بالا را ثابت نگه میدارد. اگر این نیرو را بر واحد سطح A تقسیم کنیم، عبارت حاصل تنش برشی نامیده میشود. این پارامتر با سرعت صفحه پایین (u0) متناسب و با فاصله این دو صفحه (Y) رابطه عکس دارد. بنابراین میتوان تنش برشی را به صورت یک رابطه تناسب و مطابق با معادله زیر نمایش داد.

همانطور که در رابطه بالا مشاهده میشود، ضریب ثابتی که تنش برشی و گرادیان سرعت (u0/Y) را به یکدیگر مرتبط میسازد، ویسکوزیته سیال است و با μ نمایش داده میشود. همچنین با توجه به اینکه در حالت پایا، پروفیل سرعت سیال بین دو صفحه به صورت خطی است، هر قسمت کوچک سیال نیز از رابطه خطی بالا پیروی میکند؛ بنابراین میتوان رابطه بالا را به فرم دیفرانسیلی زیر نمایش داد.
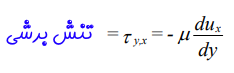
همانطور که در مبحث معادلات ناویر استوکس بیان شد، تنش برشی با دو حرف به صورت زیروند نشان داده میشود که حرف اول بیان کننده سطحی است که تنش برشی بر آن اعمال میشود (بردار نرمال عمود بر این سطح در اینجا y است) و حرف دوم جهتی که تنش برشی اعمال میشود (در اینجا تنش برشی در جهت x وارد میشود)، را نمایش میدهد.
نکته دیگری که باید به آن اشاره کرد این است که علامت منفی در عبارت بالا، بیان میکند که تنش برشی از ناحیهای که سرعت آن زیاد است به ناحیهای با سرعت پایین اعمال میشود و در واقع جهت این تنش برشی در خلاف جهت گرادیان سرعت قرار دارد.
معادلهای که در بالا نشان داده شده (رابطه ۳)، «قانون ویسکوزیته نیوتن» (Newton's Law of Viscosity) یا قانون لزجت نیوتن نامیده میشود. این قانون بیان میکند که تنش برشی بین دو لایه چسبیده سیال با منفی گرادیان سرعت بین این دو لایه متناسب است.
از فیزیک پایه داریم :
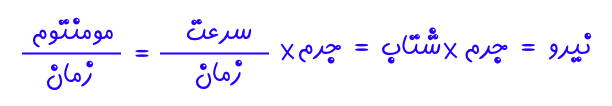
بنابراین میتوان نتیجه گرفت که تنش برشی در رابطه ۳، نرخ مومنتوم منتقل شده در واحد سطح بین دو صفحه به هم چسبیده سیال را نیز بیان میکند و این عبارت با منفی گرادیان سرعت بین این دو لایه سیال متناسب است.
در مکانیک سیالات به نسبت نرخ یک متغیر معلوم به واحد سطح «شار» (Flux) گفته میشود. برای مثال «دیمانسیون» (Dimension) شار جرمی برابر با Mt-1L-2 است. نکته دیگری که باید به آن اشاره کرد این است که تغییرات یک متغیر دلخواه را در واحد طول، «گرادیان» (Gradient) مینامند بنابراین دیمانسیون گرادیان جرم برابر با ML-1 است.
در صورتی که رابطه ۳ را در چگالی سیال ضرب و تقسیم کنیم، قانون ویسکوزیته نیوتن به شکل زیر بازنویسی میشود.
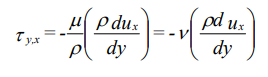
و این رابطه را برای یک جریان تراکم ناپذیر به فرم زیر میتوان بیان کرد.
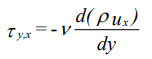
این رابطه بیان میکند که «شار مومنتوم» (Momentum flux) با منفی مقدار گرادیان شار جرم متناسب است. علاوه بر این، در معادلات بالا، متغیر جدیدی معرفی شد که رابطه آن به شکل زیر قابل نمایش است.
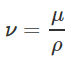
رابطه بالا «ویسکوزیته سینماتیک» (Kinematic Viscosity) سیال را نشان میدهد و دیمانسیون آن برابر با L2t-1 است. در مطالب بعدی وبلاگ فرادرس خواهید دید که دیمانسیون ویسکوزیته سینماتیک، «دیفیوژن حرارتی» (Thermal Diffusivity) و «دیفیوژن مولکولی» (Molecular Diffusivity) یکسان است. بنابراین با استفاده از آنالوژی، میتوان متوجه شد که ویسکوزیته سینماتیک، دیفیوژن مومنتوم را نشان میدهد. به عبارت دیگر میتوان بیان کرد که ویسکوزیته سینماتیک توانایی سیال برای انتقال مومنتوم را بیان میکند.
واحد ویسکوزیته سینماتیک در سیستم SI، برابر با m2s-1 است. این عبارت بسیار واحد بزرگی است و به ندرت در مسائل، مورد استفاده قرار میگیرد و به جای آن، واحد cm2s-1 به کار برده میشود. این واحد را به افتخار دانشمند معروف ایرلندی، با نام «استوکس» (Stokes) نمایش میدهند. ارتباط بین واحدهای بیان شده، در روابط زیر با جزئیات مورد مطالعه قرار گرفتهاند.
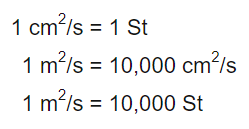
از آنجایی که اکثر سیالات، ویسکوزیته سینماتیک بسیار پایینی دارند واحد دیگری به نام سانتی استوکس نیز به شکل زیر در مسائل مختلف مورد بررسی قرار میگیرد.
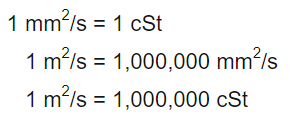
نکاتی که در بالا به بررسی آن پرداخته شد، برای حالتی کاربرد دارد که در آن سیال در یک جهت خاص جریان دارد. ولی در مسائل واقعی، سیال در سه جهت y ، x و z در حال جریان است. در این شرایط، شش تنش برشی در جهات مختلف، به سیال مورد نظر وارد میشود که این تنشها به شکل زیر قابل بیان هستند.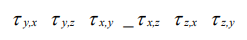
به این تنشها، «تنشهای مماسی» (Tangential Stresses) گفته میشود. علاوه بر این تنشها، سه «تنش عمودی» (Normal Stresses) نیز در سیال دیده میشود که میتوانند کششی و یا فشاری باشند. تنشهای کششی با علامت مثبت و تنشهای فشاری با علامت منفی نمایش داده میشوند.
با قرار دادن دیمانسیون نیرو، مساحت، طول و سرعت در رابطه ۳ متوجه میشویم که دیمانسیون ویسکوزیته به فرم ML-1t-1 قابل بیان است. در سیستم متریک، واحد ویسکوزیته، «پوز» (Poise) در نظر گرفته میشود و اگر آن را به صد قسمت تقسیم کنیم، واحد نهایی برابر با «سانتی پوز» (Centipoise) خواهد بود.
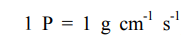
در سیستم SI، ویسکوزیته، اغلب با واحد kgm-1s-1 و گاهی نیز با واحد Nm-2s و یا Pa s بیان میشود. واحد ویسکوزیته در سیستم SI برابر با 10 پوز و یا 1000 سانتی پوز است. عبارات زیر به مقایسه واحدهای گوناگون ویسکوزیته در مسائل مختلف میپردازد.

تمام گازها و مایعات اعم از فلزات مذاب و سیالات با دمای بالا که از قانون ویسکوزیته نیوتن پیروی میکنند، «سیالات نیوتنی» (Newtonian Fluid) نامیده میشوند. در سمت مقابل، سیالهایی مانند چسبها و رنگها نیز وجود دارند که از قانون ویسکوزیته نیوتن پیروی نمیکنند. این سیالها به «سیالات غیر نیوتنی» (Non-Newtonian Fluid) معروف هستند.
در شکل زیر، نمودار تنش برشی بر حسب گرادیان سرعت در سیالات نیوتنی رسم شده است. همانطور که مشاهده میشود شیب نمودار در یک سیال نیوتنی خاص، مقدار ثابتی است که ویسکوزیته آن را نشان میدهد. این ویسکوزیته (μ) را اصطلاحا «ویسکوزیته دینامیک» (Dynamic Viscosity) نیز مینامند.
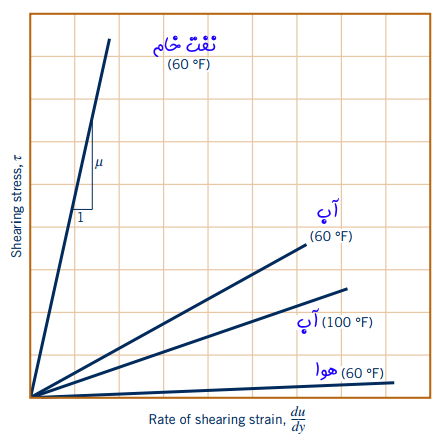
توجه شود که نمودار بالا برای سیالات غیر نیوتنی به صورت غیر خطی در خواهد آمد. در مطالب بعدی وبلاگ فرادرس به بررسی دقیق سیالات غیر نیوتنی پرداخته میشود.
شیوه اندازهگیری ویسکوزیته
جریان درون یک لوله دایروی را میتوان با استفاده از یک رابطه ریاضی ساده توصیف کرد که توسط فیزیکدان و روانشناس فرانسوی به نام «پوازی» (Jean Poiseuille) محاسبه شده است. این رابطه در مقالهای دیگر به صورت مستقل توسط مهندس هیدرولیک آلمانی به نام «هاگن» (Gotthilf Hagen) مورد مطالعه قرار گرفت.
همانطور که اشاره شد، طبق قاعده، این معادله باید با نام «معادله هاگن-پوازی» (Hagen-Poiseuille Equation) شناخته شود ولی به صورت رایج در مسائل و علوم مختلف مرتبط با مهندسی مکانیک، این معادله را به فرم خلاصه شده «معادله پوازی» (Poiseuille's Equation) نیز مینامند. در مطالب بعدی وبلاگ فرادرس به بررسی روند محاسبه این معادله پرداخته میشود. دبی حجمی سیال برای جریان «غیر آشفته» (Non-Turbulent) و «غیر ضربانی» (Non-Pulsatile) در یک لوله مستقیم یکنواخت، براساس معادله هاگن-پوازی به شکل زیر به دست میآید.
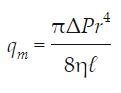
همانطور که مشاهده میشود، طبق این رابطه، دبی سیال (qm) در یک لوله با اختلاف فشار بین دو انتهای آن (ΔP) متناسب است و با طول آن (l) رابطه عکس دارد. نکته دیگری که باید اشاره کرد این است که هرچه ویسکوزیته (μ) سیال بیشتر باشد، مقدار دبی در این لوله کمتر میشود و در نهایت از این رابطه میتوان نتیجه گرفت که دبی جریان با توان چهارم شعاع لوله (r4) رابطه مستقیم دارد.
با سادهسازی معادله هاگن-پوازی، میتوان رابطهای به شکل زیر برای ویسکوزیته سیال بیان کرد.
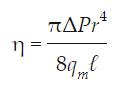
بنابراین در صورتی که سیالی درون یک لوله با شعاع r و طول l، به صورت غیر آشفته و غیر ضربانی جریان داشته باشد، با محاسبه آزمایشگاهی دبی حجمی سیال گذرنده از این لوله و اختلاف فشار دو طرف آن و قرار دادن مقادیر مربوطه در رابطه بالا، ویسکوزیته سیال قابل محاسبه خواهد بود.
پارامترهای موثر در ویسکوزیته
ویسکوزیته سیالات نیوتنی با دما و فشار آنها رابطه دارد. در صورتی که ویسکوزیته یک مخلوط مد نظر ما باشد، ویسکوزیته این مخلوط به نوع ترکیب مواد تشکیل دهنده آن نیز بستگی دارد.
برای مثال، ویسکوزیته «دی اکسید کربن» (Carbon Dioxide) به عنوان تابعی از فشار و دما در شکل زیر رسم شده است.
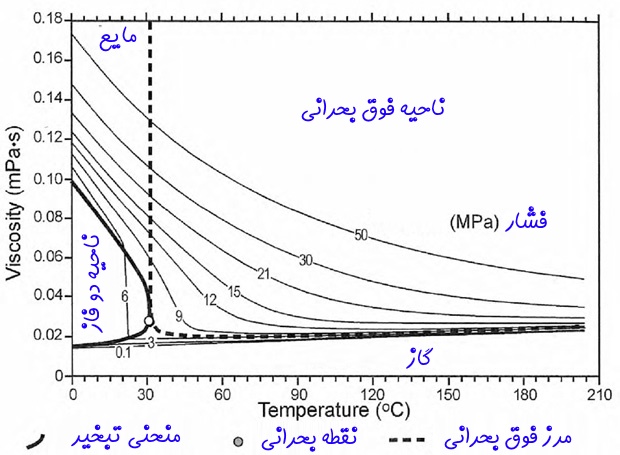
مشاهده میشود که کمترین مقدار ویسکوزیته کربن دی اکسید در دمای بحرانی دیده میشود که طبق شکل برابر با 304.1K است و این دما بالاترین دمایی تلقی میشود که در آن کربن دی اکسید حالت مایع خود را حفظ میکند. فشار بحرانی نیز در این گاز برابر با 73.8bar و یا 72.9atm است.
نکته دیگری که از شکل بالا میتوان متوجه شد این است که در دماهای بالا، فشار تاثیر کمی در ویسکوزیته دارد و در ناحیهای که کربن دی اکسید گاز است، با افزایش دما، ویسکوزیته نیز افزایش مییابد. این نمودار نمونهای از بررسی پارامترهای مؤثر در فازهای گاز و مایع سیالات است. روند مشابهی برای تمام سیالات و با استفاده از نمودارهای ویسکوزیته آنها قابل انجام است.
توجه کنید که به صورت کلی ویسکوزیته مایعات با افزایش دما، کاهش مییابد و ویسکوزیته گازها با افزایش دما، افزایش پیدا میکند.
تخمین ویسکوزیته گازها
زمانی که دادههای تجربی برای ویسکوزیته یک گاز موجود نیست، میتوان ویسکوزیته این گاز را با استفاده از مدلهای تئوری محاسبه کرد. به صورت کلی رابطهای تحت عنوان تئوری مولکولی گازها برای پیشبینی خواص انواع گاز مورد استفاده قرار میگیرد.
بنابراین با استفاده از این رابطه میتوان ویسکوزیته یک گاز را با دقت خوبی برای محاسبات مهندسی پیشبینی کرد. برای مثال رابطه زیر، ویسکوزیته مولکولهای «شبه کروی» (Quasi-Spherical) را بیان میکند.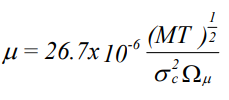
μ در این رابطه ویسکوزیته با واحد پوز را نشان میدهد و M، جرم مولکولی در واحد گرم را بیان میکند. T و σc نیز به ترتیب نشان دهنده دما مطلق در واحد کلوین و قطر برخورد در واحد آنگستروم هستند. Ωμ انتگرال برخورد را نشان میدهد که تابعی از رابطه زیر است.
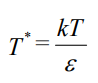
در معادله بالا، k ثابت بولتزمن را نشان میدهد که مقدار آن با استفاده از رابطه زیر بیان میشود.
در رابطه بالا ε، پارامتر انرژی برای بیان برخورد بین مولکولها است که واحد آن به شکل kgm2s-2 بیان میشود. مقادیر عددی پارامترهای σc و ε برای گازهای مختلف در منابع گوناگون موجود هستند. در صورتی که این مقادیر برای گاز خاصی موجود نباشند میتوان مقدار این دو پارامتر را با استفاده از رابطه تجربی زیر محاسبه کرد.
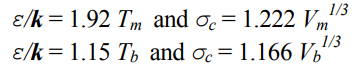
در رابطه بالا، Tm و Tb به ترتیب دمای ذوب و جوش را در واحد کلوین بیان میکنند. Vm و Vb نیز در این رابطه، به ترتیب نشان دهنده حجم مولی ذرات در دمای ذوب (حالت جامد ذرات) و جوش (حالت مایع ذرات) هستند. توجه کنید که Vm و Vb در رابطه بالا با استفاده از واحد cm3mol-1 بیان میشوند.
علاوه بر روابطی که در بالا بیان شدند، روابطی نیز برای محاسبه ویسکوزیته مخلوط گازها موجود هستند که میتوانند با دقت معقولی، ویسکوزیته نهایی مخلوط را تخمین میزنند. یکی از روابط که به صورت «نیمه تجربی» (Semi-Empirical) استخراج شده و ویسکوزیته یک مخلوط گاز در فشارهای کم و متوسط را بیان میکند به شکل زیر است.
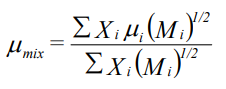
Xi در این رابطه، کسر مولی جز i ام که ویسکوزیته آن μi است را بیان میکند و Mi نیز نشاندهنده وزن مولکولی جز i ام است.
تخمین ویسکوزیته مایعات
بر خلاف گازها، مدلهای کمی برای پیشبینی ویسکوزیته مایعات نیز به وجود آمدهاند و این مدلها به صورت کیفی قادر به پیشبینی ویسکوزیته مایعات مختلف هستند.
ویسکوزیته مایعات نسبت به ویسکوزیته گازها به شدت خواص متفاوتی از خود نشان میدهند. برای مثال، با افزایش دما، ویسکوزیته مایعات کاهش مییابد. رابطه ویسکوزیته مایعات با استفاده از «معادله آرنیوس» (Arrhenius-type Equation) به شکل زیر بیان میشود.
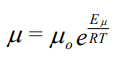
در رابطه بالا μ0، ویسکوزیته را در دمای مرجع نشان میدهد و Eμ، ضریب دما برای سیال است. ضریب دمای ویسکوزیته، مفهوم فیزیکی مانند انرژی اکتیواسیون را بیان میکند بنابراین مقدار در مایعات بر خلاف گازها با افزایش دما، افزایش مییابد.
نکته دیگر در تفاوت ویسکوزیته مایعات و گازها این است که تخمین ویسکوزیته مخلوط مایعات بر خلاف مخلوط گازها کار بسیار پیچیدهای است و به نوع مایعات و در صد ترکیب آنها کاملا مرتبط است و روابط آن با استفاده از آزمایشات مختلف تجربی قابل محاسبه است. برای مثال در ادامه روشهای Gambill و Refutas که به صورت گسترده در صنایع نفت کاربرد دارد مورد بررسی قرار میگیرند.
در سال 1959، Gmabill معادله زیر را برای تخمین ویسکوزیته سینماتیک مخلوطی از دو مایع بیان کرد.

در این رابطه ν، ویسکوزیته سینماتیک، x کسر جرمی و v کسر حجمی دو مایع در مخلوط مورد نظر را نشان میدهند.
در سال 2000 Refutas، مطالعهای را برای تخمین مخلوطی از دو یا چند مایع مختلف انجام داد. در این روش پارامتر تحت عنوان، «عدد ترکیب ویسکوزیته» (Viscosity Blending Number) تعریف میشود و به طور خلاصه میتوان آن را با استفاده از نماد VBN نمایش داد. این پارامتر برای هرکدام از اجزای این مخلوط مورد محاسبه قرار میگیرد و در نهایت از آنها برای محاسبه عدد ترکیب ویسکوزیته کل مخلوط استفاده میشود.
عدد ترکیب ویسکوزیته اجزای این مخلوط با استفاده از رابطه زیر محاسبه میشود.
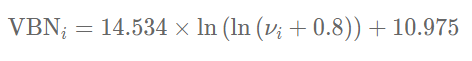
در ادامه، عدد ترکیب ویسکوزیته نهایی مخلوط مذکور با استفاده از رابطه زیر قابل محاسبه است.
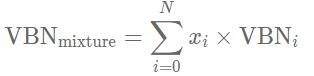
در نهایت برای محاسبه ویسکوزیته سینماتیک مخلوط، از رابطه زیر استفاده میشود.
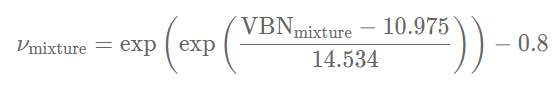
معادلات Refutas در حالتی که کسر حجمی سیال مورد نظر داده شده باشد نیز قابل بازنویسی هستند که این روابط توسط Chevron محاسبه شدهاند. در این روش از شاخص ترکیب ویسکوزیته (Viscosity Blend Index) استفاده میشود که مقدار آن برای هر جز مخلوط به شکل زیر قابل بیان است.
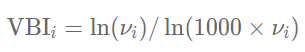
در ادامه، شاخص ترکیب ویسکوزیته این مخلوط با استفاده از رابطه زیر قابل محاسبه است.
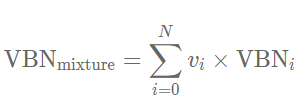
در نهایت با استفاده از این رابطه میتوان ویسکوزیته مخلوط را مشابه با روش اصلی Refutas محاسبه کرد.
همانطور که اشاره شد ویسکوزیته، پارامتری است که میزان مقاوت سیال (مایع یا گاز) در مقابل جاری شدن را نشان میدهد. این پارامتر در گازها و مایعات از روابط مختلف پیروی میکند و به فشار و دمای سیال وابسته است. در این مقاله ابتدا مفهوم ویسکوزیته مورد بررسی قرار گرفت و در ادامه روابط مختلف حاکم بر آن، شیوه اندازهگیری و پارامترهای مؤثر در آن بیان شدند و در نهایت به بررسی روابط حاکم بر ویسکوزیته مایعات، گازها و مخلوطها پرداخته شد. در مطلب سیال غیر نیوتنی وبلاگ فرادرس به بررسی ویسکوزیته و سایر ویژگیهای سیالات غیر نیوتنی پرداخته میشود.
در صورتی که قصد یادگیری بیشتر در زمینه مکانیک سیالات را دارید، آموزشهای زیر از سایت و مجله به شما پیشنهاد میشود:
- سیال غیر نیوتنی (Non Newtonian Fluid) — از صفر تا صد
- جریان توسعه یافته (Fully Developed Flow) — به زبان ساده
- تحلیل ابعادی (Dimensional Analysis) در مکانیک سیالات — به زبان ساده
- توربوماشین (Turbomachinery) — به زبان ساده
- پیوستگی و بقای جرم در سیالات — از صفر تا صد
- معادلات ناویر استوکس (Navier Stokes) — از صفر تا صد
^^












کمترین میزان گرانروی (لزجت) که بشر به آن رسیده از آن کدام سیال است؟!
سپاس و درود فراوان. کمک کننده بود.
کاش دفترچه سازمان استاندارد رو برای انجام این آزمایش میذاشتین برای دانلود
منظور از انتگرال برخورد و قطر برخورد و فاکتور انرژی چیست؟
سلام خسته نباشید
وقتتون بخیر
رابطه ی بین لزجت و چسبندگی سیال به چه صورت هست؟
ممنون میشم یه توضیحی بدید
سلام وقت بخیر
دلیل این که رابطه ویسکوزیته با دما در مایعات و گازها متفاوته چیه؟
معادله دو مشکل دارد- لطفا چک شود- فقط در یک صورت صحیح است مه میو برابر یک باشد و اگر میو را هم برابر یک بگیریم معادله بیهوده است
با تشکر
با سلام؛
معادلهها بررسی شد و اشکالی در آنها یافت نشد. لطفا به پارامترهای معادله مورد نظر دقت کنید. در صورت رفع نشدن مشکل، ممنون میشویم اگر عنوان معادله مورد نظر را بنویسید تا آن را مجددا مورد بررسی قرار دهیم.
از همراهی شما با مجله فرادرس سپاسگزاریم. سلامت و موفق باشید.
salam ey kash refrence matalebetun akhare har maghle mineveshtid
سلام، وقت شما بخیر؛
اگر دقت بفرمائيد منابع تمامی مقالات مجله فرادرس در انتهای آنها و بعد از بخش پیشنهاد مطالب و آموزشهای مرتبط و مشابه ذکر شده است.
از اینکه با مجله فرادرس همراه هستید از شما بسیار سپاسگزاریم.
ممنون کمک کننده بود
با تشکر از سايت خيلي خوبتون …