ژیروسکوپ چیست و چگونه کار می کند؟ — به زبان ساده

در این مطلب در مورد ژیروسکوپ و فیزیک آن صحبت میکنیم. شاید برای شما هم این سوال پیش آمده باشد که چرا دوچرخه در حالت سکون به زمین میافتد، ولی دوچرخه در حال حرکت میتواند تعادل خودش را حفظ کند؟ فیزیک ژیروسکوپ (Gyroscope) یکی از مفاهیم دشوار فیزیک است که درک آن، به دقت و توجه زیادی نیاز دارد. این مطلب به فیزیک ژیروسکوپ، کاربردهای آن و تاریخچه ژیروسکوپ اختصاص دارد.
ژیروسکوپ چیست؟
ژیروسکوپ دستگاهی است که شامل یک چرخ سریع یا پرتویی چرخان از نور است که برای تشخیص انحراف یک جسم از جهت مورد نظر خود استفاده میشود. ژیروسکوپها در قطب نما و خلبانان اتوماتیک در کشتیها و هواپیماها، در مکانیسمهای هدایت اژدرها و در سیستمهای هدایت داخلی نصب شده در وسایل پرتاب فضایی، موشکهای بالستیک و ماهوارههای در حال چرخش استفاده میشوند. ژیروسکوپها را به دو دسته کلی تقسیم میکنیم که عبارت از ژیروسکوپ مکانیکی و ژیروسکوپ اپتیکی هستند که در ادامه انواع ژیروسکوپ را معرفی میکنیم.
ژیروسکوپ مکانیکی چیست؟
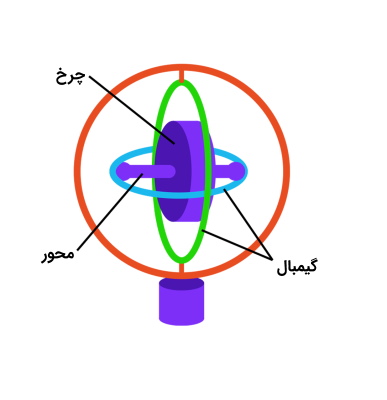
ژیروسکوپهای مکانیکی بر اساس اصل کشف شده در قرن نوزدهم توسط «ژان برنارد لئون فوکو» (Jean-Bernard-Léon Foucault)، فیزیکدان فرانسوی که نام ژیروسکوپ را به چرخ یا روتور نصب شده در حلقههای جیمبال یا گیمبال داده بود، نامگذاری و شناخته شدند. تکانه زاویهای روتور در حال چرخش باعث شد تا حتی زمانی که مجموعه جیمبال کج بود، حالت خود را حفظ کند. در دهه 1850 فوکو آزمایشی را با استفاده از چنین روتوری انجام داد و نشان داد که چرخ در حال چرخیدن جهت اصلی خود را در فضا بدون توجه به چرخش زمین حفظ میکند.
این قابلیت کاربردهای متعددی را برای ژیروسکوپ به عنوان نشانگر جهت پیشنهاد کرد و در سال 1908 اولین ژیروسکوپ قابل کار توسط مخترع آلمانی «آنشوتز کیمفه» (H. Anschütz-Kaempfe) برای استفاده در شناور توسعه یافت. در سال 1909، مخترع آمریکایی «المر. اسپری» (Elmer A. Sperry)، اولین خلبان اتوماتیک را با استفاده از ژیروسکوپ برای حفظ هواپیما در مسیر ساخت. اولین خلبان اتوماتیک کشتیها در کشتی مسافری دانمارکی توسط یک شرکت آلمانی در سال 1916 نصب شد و در همان سال از ژیروسکوپ در طراحی اولین افق مصنوعی هواپیماها استفاده شد.
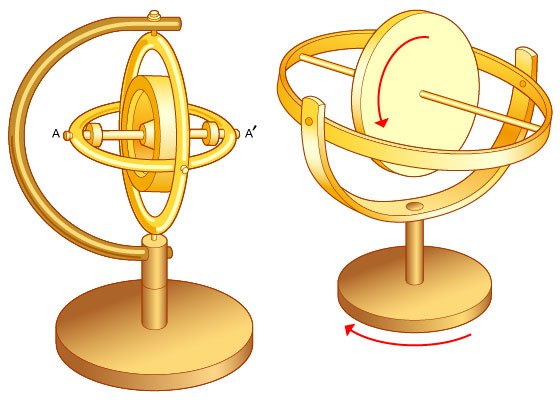
ژیروسکوپها از زمان موشکهای V-1 و V-2 آلمانها در جنگ جهانی دوم برای هدایت خودکار، تصحیح حرکت از راه دور و چرخش در موشکهای کروز و بالستیک استفاده میشوند. همچنین در طول این جنگ، توانایی ژیروسکوپها برای تعیین جهت با درجه بالایی از دقت، همراه با مکانیزمهای پیچیده کنترلی، منجر به توسعه تفنگهای تثبیت شده، بمب افکن و سکوهایی برای حمل اسلحه و آنتنهای راداری روی کشتیها شد. سیستمهای هدایت داخلی مورد استفاده فضاپیماهای مداری به یک سکوی کوچک نیاز دارند که با درجه فوق العادهای از دقت تثبیت شوند. این مهم توسط ژیروسکوپهای سنتی انجام میشود. دستگاههای بزرگتر و سنگینتر به نام چرخهای حرکت (یا چرخهای عکس العمل) نیز در سیستمهای کنترل جهت جغرافیایی برخی از ماهوارهها استفاده میشوند.
ژیروسکوپ نوری یا اپتیکی چیست؟
ژیروسکوپهای نوری، بدون قطعات متحرک، در هواپیماهای جت تجاری، موشکهای تقویت کننده یا بوستر و ماهوارههای در حال چرخش استفاده میشوند. چنین دستگاههایی بر اساس اثر «سایناک» (Sagnac) ساخته شدهاند و اولین بار توسط دانشمند فرانسوی «جرجز سایناک» (Georges Sagnac) در سال 1913 به جامعه معرفی شدند. در چیزی که سایناک ارائه داد، یک پرتو نوری به شکلی تقسیم شد که بخشی در جهت عقربههای ساعت و بخشی در جهت خلاف جهت عقربههای ساعت در اطراف یک سکوی چرخشی حرکت میکرد. اگر چه هر دو پرتو در یک حلقه بسته حرکت میکردند، اما پرتویی که در جهت چرخش سکو حرکت میکرد، کمی بعد از اینکه پرتوی مخالف چرخش حرکت سکو به نقطه آغازین بازگشت، به نقطه مبداء بازگشت. در نتیجه یک الگوی تداخل متناوب (نوارهای متناوب روشن و تاریک) تشخیص داده شد که بستگی به میزان دقیق چرخش صفحه گردان دارد.
ژیروسکوپهای مورد استفاده از اثر سایناک در دهه 1960 و پس از اختراع لیزر و توسعه فیبر نوری شروع به تکامل و پیشرفت کردند. در ژیروسکوپ لیزری حلقهای، پرتوهای لیزر منحرف و تقسیم شده و سپس از طریق سه حلقه توخالی عمود بر هم متصل به وسیله نقلیه در مسیرهای مخالف هدایت میشوند. در واقع حلقهها معمولاً مثلث، مربع یا مستطیل هستند که از گازهای بی اثر پر شدهاند و از طریق آنها پرتوها بر روی آینه منعکس میشوند. همان طور که وسیله نقلیه حرکت چرخشی یا گام برداشتن را انجام میدهد، الگوهای تداخلی ایجاد شده در حلقههای مربوط به ژیروسکوپ توسط سلولهای فوتوالکتریک اندازه گیری میشوند. سپس الگوهای هر سه حلقه به منظور تعیین میزان چرخش جسم در سه بعد به صورت عددی یکپارچه میشوند. نوع دیگر ژیروسکوپ نوری ژیروسکوپ فیبر نوری است که از لولهها و آینههای توخالی استفاده میکند و نور را از طریق الیاف نازکی که محکم در اطراف یک قرقره کوچک پیچیده شده است عبور میدهد.
ژیروسکوپهای سیستمهای میکروالکترومکانیکی (MEMS)
ژیروسکوپهای MEMS در اصل ژیروسکوپهای کوچکی هستند که در دستگاههای الکترونیکی یافت میشوند. این ژیروسکوپها بر اساس ایده آونگ فوکو ساخته شدهاند و از یک عنصر ارتعاشی استفاده میکنند.
ژیروسکوپ تشدید کننده نیمکره (HRG)
HRG همچنین به عنوان ژیروسکوپ لیوان نوشیدنی یا ژیروسکوپ قارچ شناخته میشود، این ژیروسکوپ از یک پوسته نازک نیمکرهای حالت جامد استفاده میکند که توسط یک تنه ضخیم ثابت شده است. این پوسته که توسط نیروهای الکترواستاتیک ایجاد شده، توسط الکترودهایی که به طور مستقیم بر روی ساختارهای کوارتز ذوب شده و جدا شده قرار میگیرند، یک رزونانس خمشی منتقل میشود. خاصیت اینرسی امواج ایستاده خمشی به ایجاد یک اثر ژیروسکوپی کمک میکند.
ژیروسکوپ ساختار ارتعاشی
این ژیروسکوپ همچنین به عنوان ژیروسکوپ کوریولیس ارتعاشی (CVG) شناخته میشود، ژیروسکوپ ساختار ارتعاشی یک ژیروسکوپ است که از یک ساختار ارتعاشی برای تعیین سرعت چرخش استفاده میکند.
ژیروسکوپ تنظیم شده پویا (DTG)
DTG یک روتور است که توسط یک لولای کلی با محورهای خمشی معلق شده است. سختی فنر خمشی مستقل از سرعت چرخش است. اما اینرسی پویا (از اثر واکنش ژیروسکوپی) از جیمبال، سختی منفی فنر متناسب با مربع سرعت چرخش را ایجاد میکند. بنابراین با سرعت خاصی، این دو گشتاور اثر یکدیگر را حذف کرده و روتور را از گشتاور آزاد میکنند و آن را به یک ژیروسکوپ ایده آل تبدیل میکنند.
ژیروسکوپ لیزری حلقه
یک ژیروسکوپ لیزری حلقهای از اثر سایناک برای محاسبه چرخش با اندازه گیری تغییر الگوی تداخل یک پرتو به دو نیمه، حتی زمانی که دو نیمه در جهت مخالف حلقه حرکت میکنند، استفاده میکند. در اثر سایناک، یک پرتو نور تقسیم میشود و دو پرتو به گونهای ساخته میشوند که مسیری یکسان اما در جهت مخالف را دنبال کنند. در بازگشت به نقطه ورود، دو پرتو نور اجازه خروج از حلقه و ایجاد تداخل را دارند.
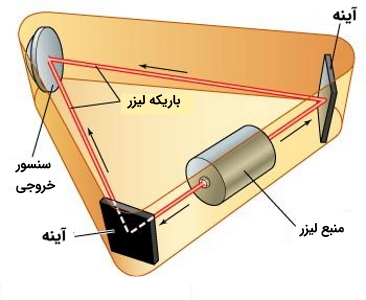
ژیروسکوپ فیبر نوری
ژیروسکوپ فیبر نوری از تداخل نور برای تشخیص چرخش مکانیکی استفاده میکند. دو نیمه پرتوی تقسیم شده در یک سیم پیچ از کابل فیبر نوری به طول 5 کیلومتر در جهت مخالف حرکت میکنند.
مختصری از تاریخچه ژیروسکوپ
در اصل، ژیروسکوپ از یک قسمت بالایی تشکیل شده که با یک جفت گیبمال ترکیب شده است. چنین ابزاری در بسیاری از تمدنهای مختلف از جمله یونان، روم و چین اختراع شد، اگر چه اکثر آنها در واقع به عنوان ابزار استفاده نمیشدند. اولین دستگاه شناخته شده مشابه ژیروسکوپ، آینه طبی یا سپکولوم چرخان (Whirling Speculum) یا «سرسونز سپکولوم» (Serson’s Speculum) بود و توسط جان سرسون در سال 1743 اختراع شد. از این دستگاه به عنوان یک سطح برای تعیین افق در شرایط مه آلود یا ابری استفاده میشد.
در سال 1817 بود که یوهان بوننبرگر آلمانی درباره استفاده از این ابزار مانند یک ژیروسکوپ واقعی نوشت. در سال 1852، لئون فوکو فیزیکدان فرانسوی، آن را در آزمایشی که شامل چرخش زمین بود، به کار برد و دستگاه را با نام امروزی خود یعنی ژیروسکوپ نامگذاری و معرفی کرد. ریشه کلمه ژیروسکوپ از کلمه یونانی skopeein به معنی دیدن و کلمه یونانی gyros، به معنی دایره یا چرخش است.
در دهه 1860، ظهور موتورهای الکتریکی امکان چرخش ژیروسکوپ را به طور نامحدود فراهم کردند. پس از آن موجی از بداهه پردازیها با اولین ژیروسکوپ کاربردی ثبت شد که در سال 1904 توسط مخترع آلمانی هرمان آنشاتز-کائمپه اختراع شد. خیلی زود ملتها از اهمیت نظامی این اختراع آگاه شدند و متوجه شدند که چگونه میتوان از ژیروسکوپها برای فرمان خودکار و اصلاح چرخش و حرکت در موشکهای کروز و بالستیک استفاده کرد.
بنابراین در طول جنگ جهانی دوم، ژیروسکوپ به یک جزء اصلی برای هدایت و کنترل هواپیماها و ضدهواییها تبدیل شد. پس از جنگ، ژیروسکوپها برای استفاده در موشکهای هدایت شونده و سیستمهای ناوبری سلاح کوچک مورد استفاده قرار گرفتند. این ژیروسکوپهای کوچک، وزنی کمتر از 85 گرم و قطر تقریبی 2/5 سانتی متر داشتند.
ژیروسکوپ چگونه کار میکند؟
ژیروسکوپ در اصل یک روتور عظیم است که در حلقههای نگهدارنده موسوم به جیمبال ثابت شده است. جیمبالها یاتاقانهای بدون اصطکاکی دارند که روتور مرکزی را از گشتاورهای خارجی جدا میکند. راستای چرخش توسط محور چرخان مشخص میشود. روتور در یک راستا میچرخد و دارای سه درجه آزادی چرخشی است. پس از تعادل کامل در سرعتهای بالا، محور چرخش با سرعت بالا روتور مرکزی خود را حفظ میکند.
حال هنگامی که به ژیروسکوپ گشتاورهای خارجی یا چرخشهای حول محور معین اعمال میشود، میتوان جهت را با استفاده از پدیده تقدم و انحراف مسیر اندازه گیری کرد. این تقدم به تغییر جهت محور چرخشی یک جسم در حال چرخش اشاره دارد. به عبارت دیگر، هنگام اعمال گشتاور خارجی بر روی جسمی که حول یک محور میچرخد، در امتداد جهت عمود بر محور چرخش تقدم ایجاد میشود.
این چرخش حول محور دوران مشخص شده و اطلاعات مربوط به این چرخش به موتور یا دستگاه دیگری منتقل میشود که گشتاور را در جهت مخالف اعمال میکند و در نتیجه حرکت پیشین را لغو کرده و جهت را حفظ میکند. همچنین میتوان با استفاده از دو ژیروسکوپ که عمود بر یکدیگر قرار گرفتهاند از تقدم جلوگیری کرد. سرعت چرخش را میتوان با نوسانی کردن گشتاور متقابل در فواصل زمانی ثابت اندازه گیری کرد.
اولین بار «لئون فوکو» (Leon Foucault)، فیزیکدان فرانسوی در سال 1852 برای نشان دادن حرکت زمین، از این ابزار استفاده کرد. هنگامی که ژیروسکوپ شروع به دوران میکند، اولین سوالی که به ذهن میرسد این است که چرا به دلیل نیروی جاذبه، روی زمین نمیافتد که در این مطلب دلیل این موضوع را بررسی میکنیم. در تصویر زیر، حرکت ژیروسکوپ نشان داده شده است.

شماتیک یک ژیروسکوپ را میتوان به صورت زیر رسم کرد. در این شکل، سرعت زاویهای ثابت دیسک با و بر حسب رادیان بر ثانیه نشان داده شده است. نشان دهنده سرعت حرکت تقدیمی (Precession) بوده و با واحد رادیان بر ثانیه اندازه گرفته میشود. طول میله با و شعاع دیسک با نشان داده شدهاند. زاویه بیانگر زاویه بین میله و خط عمود به زمین است و مقدار ثابتی دارد. هنگامی که دیسک با سرعت زاویهای دوران میکند، سرعت حرکت تقدیمی ژیروسکوپ حول لولایی که روی زمین قرار دارد، برابر با است (زاویه در این حرکت ثابت میماند). حال میخواهیم به پرسشی که در ابتدای مقاله مطرح شد، پاسخ دهیم.
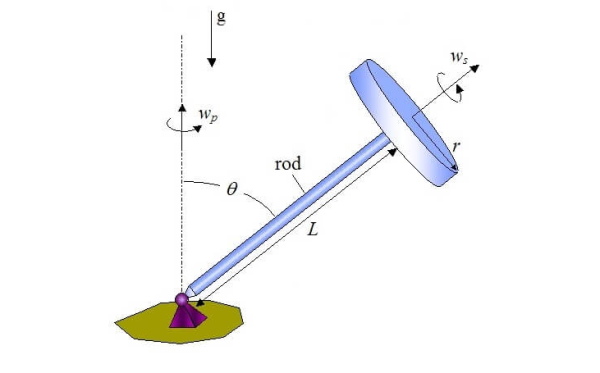
به دلیل دوران مرکب و با سرعتهای زاویهای و ، گشتاوری به دیسک دوار وارد میشود. این گشتاور با حاصل ضرب خارجی متناسب است. برای تعیین جهت این گشتاور از قانون دست راست استفاده میکنیم. در نتیجه گشتاوری در خلاف جهت حرکت عقربههای ساعت به سیستم وارد میشود. از طرفی، نیروی گرانش باعث میشود گشتاوری در جهت حرکت عقربههای ساعت به دیسک وارد شود. تقابل این دو گشتاور که خلاف جهت هم هستند، از افتادن ژیروسکوپ جلوگیری میکند. اکنون میتوانیم معادلات حرکت را برای ژیروسکوپ بنویسیم.
تحلیل ریاضی حرکت ژیروسکوپ
محورهای مختصات XYZ را به صورت شکل زیر برای ژیروسکوپ رسم میکنیم. محورهای مختصات به زمین ثابت شدهاند.
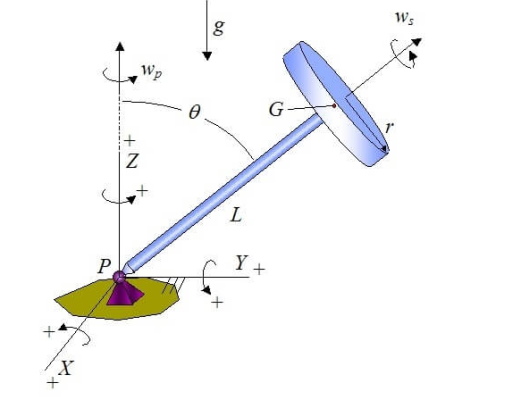
در شکل بالا، نماد شتاب گرانش است. نقطه G مرکز جرم دیسک را نشان میدهد. محل تکیهگاه نیز با P نمایش داده میشود. مبدأ مختصات XYZ، نقطه P است. بردارهای J ،I و K بردارهای یکه هستند و به ترتیب جهت مثبت محورهای Y ،X و Z را نشان میدهند. در این حالت، سرعت زاویهای دیسک نسبت به زمین به صورت زیر به دست میآید.
با مشتقگیری از رابطه بالا نسبت به زمان، شتاب زاویهای دیسک به شکل زیر محاسبه میشود.
همانطور که پیشتر نیز بدان اشاره کردیم، ثابت است. در نتیجه مشتق آن صفر میشود و برای محاسبه رابطه بالا، فقط باید از بردارهای یکه مشتق گرفت. به این ترتیب، رابطه شتاب به شکل زیر ساده میشود.
میدانیم سرعت زاویهای میله با کمک رابطه زیر محاسبه میشود.
از آنجایی که سرعت زاویهای میله ثابت است و جهت آن هم تغییر نمیکند، شتاب زاویهای آن صفر خواهد بود.
تحلیل دیسک
در این بخش میخواهیم نیروها و گشتاورهای وارد به دیسک را تحلیل کنیم. نمودار جسم آزاد دیسک در شکل زیر نشان داده شده است. در این شکل میله را از دیسک جدا کردهایم. به این نکته توجه کنید که دستگاه مختصات محلی xyz، روی دیسک ثابت شده است و به همراه آن حرکت میکند. مبدأ این دستگاه مختصات، نقطه G است. دقت کنید که محور x موازی محور X قرار دارد.
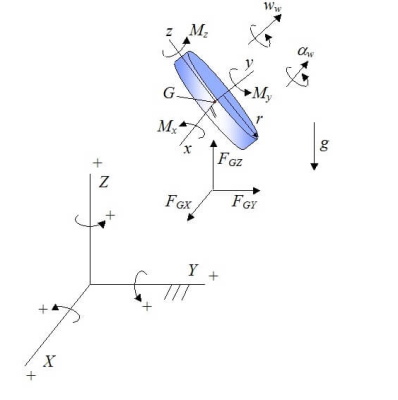
در شکل بالا، گشتاور در نقطه G و در راستای محور x را با نشان دادهایم. گشتاورهای و نیز به طریقی مشابه تعریف شدهاند. همچنین نیرو را در نقطه G و همراستا با محور X نشان میدهد. نیروهای و نیز به ترتیب با محورهای Y و Z در یک راستا قرار دارند. قانون دوم نیوتن را برای دیسک مینویسیم.
در رابطههای بالا، جرم دیسک با نمایش داده شده است. شتاب را در نقطه G و در راستای X نشان میدهد. شتابهای و نیز به طوری مشابه و به ترتیب در جهتهای Y و Z تعریف شدهاند. از آنجایی که نقطه G روی یک مسیر افقی به شکل دایره و با سرعت ثابت حرکت میکند، شتاب مماسی برابر صفر است.
در نتیجه کافیست فقط رابطههای دوم و سوم را در نظر بگیریم. حرکت نقطه G روی مسیر دایرهای، شتاب مرکزگرا ایجاد میکند. این شتاب مرکزگرا به سمت مرکز دوران است. بنابراین رابطههای شتاب و نیرو به صورت زیر نوشته میشوند.
(رابطه ۱)
از آنجایی که نقطه G با سرعت ثابت روی یک دایره افقی حرکت میکند، شتاب در راستای Z برابر با صفر است.
(رابطه ۲)
حال، معادلات حرکت اویلر را در جهت x برای جسم صلب به کار میبریم. این معادلات در دو جهت دیگر، مساوی صفر هستند. همانطور که میدانیم دستگاه مختصات xyz در جهتهای اصلی اینرسی دیسک قرار گرفتهاند.
توجه کنید که نیروهای ، و حول نقطه G هیچ گشتاوری ایجاد نمیکنند. زیرا هر سه نیرو از نقطه G عبور میکنند و طول بازوی گشتاور در آنها صفر است. در رابطه بالا، ، و ، به ترتیب ممانهای اینرسی را حول نقطه G در جهتهای y ،x و z نشان میدهد. مقدار ممانهای اینرسی دیسک به دلیل تقارن، به صورت زیر محاسبه میشوند.
در نتیجه معادله حرکت اویلر در جهت x به دست خواهد آمد.
(رابطه ۳)
تحلیل میله
در این بخش گشتاورهای وارد شده به میله را حول نقطه P بررسی خواهیم کرد. نمودار جسم آزاد میله به صورت زیر رسم شده است. دستگاه مختصات xyz طوری رسم شده که بتواند با میله حرکت کند. مبدأ این دستگاه در نقطه P قرار دارد. همچنین محورهای این دستگاه نیز در راستای جهتهای اصلی اینرسی میله قرار گرفتهاند.
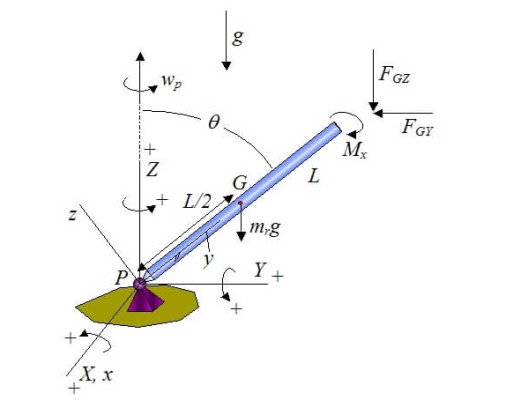
نقطه P به عنوان یک لولای بدون اصطکاک در نظر گرفته شده است. در نتیجه هیچ گشتاوری روی میله ایجاد نخواهد کرد. به منظور محاسبه برآیند گشتاور در نقطه P، معادله حرکت اویلر را در جهت x مینویسیم.
سرعت و شتاب زاویهای میله در دستگاه xyz را میتوان به صورت زیر نوشت.
در رابطه بالا، ، و ، به ترتیب ممانهای اینرسی میله را حول نقطه P در جهتهای y ،x و z نشان میدهند. ممانهای اینرسی میله به صورت زیر قابل محاسبه هستند. در رابطههای زیر جرم میله را نشان میدهد.
در نتیجه معادله حرکت اویلر در جهت x به صورت زیر نوشته میشود.
(رابطه ۴)
با ادغام رابطههای ۱ تا ۴ به نتیجه زیر میرسیم.
حال میتوان این رابطه را برای هریک از پارامترهای ، و حل کرد و هریک را برحسب دو پارامتر دیگر به دست آورد.
پایداری ژیروسکوپ
با توجه به مباحث مطرح شده در تکانه زاویهای، تغییرات بردار تکانه زاویهای جسم صلب در بازه زمانی تا به صورت زیر محاسبه میشود. پارامتر بردار تکانه زاویهای را در لحظه نهایی نشان میدهد. بردار تکانه زاویهای در لحظه اولیه نیز برابر با است. بردار هم بیانگر گشتاورهای خارجی وارد به جسم صلب است.
با اینکه رابطه بالا برای جسم صلب تعریف شده است، میتوان آن را برای هر سیستمی از ذرات نیز به کار برد. برای اثبات این موضوع میتوانید به کتابهای کلاسیک در حوزه مهندسی مکانیک مراجعه کنید. این رابطه در دو مورد به کار میرود. یکی هنگامی که مبدأ محورهای محلی xyz در مرکز جرم G مربوط به جسم صلب قرار گرفته باشد. در حالت دوم، این مبدأ میتواند در نقطه O که روی جسم صلب ثابت است (در صورت وجود) قرار داده شود. در ادامه این بخش، از حالت اول استفاده شده است. بنابراین، گشتاورها، مقادیر اینرسی و تکانه زاویهای نسبت به نقطه G سنجیده خواهند شد.
برای نشان دادن پایداری ژیروسکوپ، جسم صلبی را مانند یک دیسک در نظر بگیرید که تقارن محوری دارد. این جسم در لحظه مورد نظر، با سرعت زاویهای در حال دوران است.
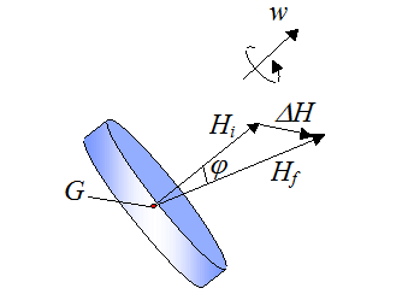
در شکل بالا، تغییر بردار تکانه زاویهای بین زمانهای و با نشان داده شده است. با توجه به رابطه قبلی، این مقدار برابر با ضربه خارجی است.
با ثابت بودن مقدار ، کاهش زاویه φ موجب افزایش مقدار میشود. یعنی هرچه مقدار تکانه زاویهای اولیه بیشتر باشد، مقدار زاویه φ برای تغییر به مقدار ثابت، کوچکتر خواهد بود. در نتیجه، اندازه بردار تکانه زاویهای با اندازه بردار سرعت زاویهای متناسب است. به عبارت دیگر هرچه سرعت چرخش جسم به دور خود بیشتر شود، زاویه φ کوچکتر میشود.
اگر هیچ گشتاور خارجی به جسم وارد نشود، و زاویه φ صفر خواهد بود. در این حالت حرکت جسم، بدون گشتاور است. بنابراین، اندازه و جهت بردار تکانه زاویهای ثابت میماند و تکانه زاویهای پایستار است.
در جسم صلبی که دارای حرکت بدون گشتاور است، محور حرکت تقدیمی، منطبق بر بردار تکانه زاویهای دیده میشود. محور حرکت تقدیمی، جهتگیری جسم را تعیین میکند. در نتیجه، هرگونه تغییر کوچک در جهت بردار تکانه زاویهای موجب تغییر کوچکی در جهتگیری جسم میشود. یعنی پس از اینکه ضربه خارجی اعمال شود، بار دیگر حرکت جسم، بدون گشتاور میشود.
به این ترتیب، هرگاه به جسمی که دارای تقارن محوری است و با سرعت زیاد (بدون گشتاور) به دور خود میچرخد، ضربه خارجی وارد شود، جسم قادر است محور حرکت تقدیمی را با تغییری جزئی حفظ کند.
کاربرد اثر ژیروسکوپی در دنیای واقعی
درک ماهیت عملکرد ژیروسکوپ این موضوع را مشخص میکند که چرا برای جهتیابی، از یک دیسک دوار (که از طریق یک موتور تغذیه میشود) درون یک قاب فلزی (جیمبال) استفاده میشود. دیسک دوار درون قاب فلزی نصب میشود تا هیچگونه گشتاور خارجی به آن وارد نشود. بنابراین، جهتگیری آن، به جز یک مقدار ناچیز، تغییری نخواهد داشت. همین عامل موجب میشود ژیروسکوپ در سیستمهای ناوبری کشتیها و قایقها به وفور به کار رود. در این حالت، حتی اگر مسیر حرکت کشتی هم عوض شود، جهتگیری ژیروسکوپ بدون تغییر میماند. شکل زیر یک نمونه سیستم ژیروسکوپ-جیمبال را نشان میدهد.
پایداری ژیروسکوپ را میتوان در حرکت پرتابه نیز بررسی کرد. به عنوان یک مثال آشنا، توپ استفاده شده در فوتبال آمریکایی را در نظر بگیرید که هم تقارن محوری دارد و هم پس از پرتاب، به دور خودش میچرخد. فرض کنید این توپ به درستی پرتاب شود. در این حالت مطابق شکل زیر، راستای محور طولی آن در حین پرواز تغییر نمیکند. چرخش توپ به دورِ خود در پاسخ به نیروهای آیرودینامیکی، اثر ژیروسکوپی ایجاد میکند. در این مثال، با ترکیبی از شتاب ژیروسکوپی، نیروهای آیرودینامیکی ناشی از درگ (Drag) و لیفت (نیروی برا) روبرو هستیم. در اینجا به دنبال تحلیل این مسأله پیچیده نیستیم و این مثال فقط به عنوان کاربردی از اثر ژیروسکوپ در دنیای واقعی ارائه شد.
در ادامه، موضوع دیگری را بررسی میکنیم. جسم صلبی را در نظر بگیرید که حرکت بدون گشتاور دارد. در این حالت از دید ناظری که در دستگاه مختصات لخت قرار دارد، اینگونه به نظر میرسد که محور حرکت تقدیمی بر بردار تکانه زاویهای منطبق است. در حالی که میدانیم این محور ثابت بوده و اندازه و جهت آن تغییر نمیکند.
تحلیل ریاضی اسپین خالص در ژیروسکوپ
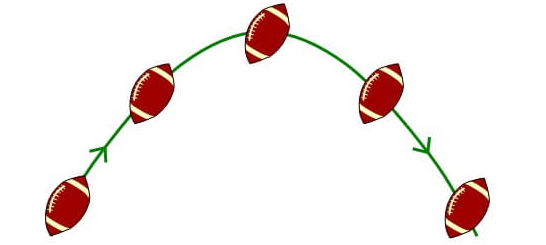
بار دیگر به محاسبات ریاضی برمیگردیم. شکل زیر را در نظر بگیرید که محورهای مختصات محلی xyz مطابق آن تعریف شده است.
میخواهیم رابطهای برای ارتباط بین زاویه و بردارهای و پیدا کنیم. با استفاده از ضرب داخلی، رابطه زیر به راحتی به دست میآید.
در این رابطه، ، تکانه زاویهای حول مرکز G است. با یک بار مشتقگیری از این رابطه برحسب زمان، نتیجه زیر حاصل میشود.
با جاگذاری عبارت در رابطه بالا و استفاده از مفهوم ضرب خارجی، رابطه قبل را میتوان به این صورت نوشت.
براساس رابطه به دست آمده، هنگامی که مقادیر و با یکدیگر برابر باشند (هر دو برابر با )، صفر خواهد بود. مانند اتفاقی که برای جسم چرخان در فضا رخ میدهد. حال فرض کنید زاویه α صفر باشد. در این حالت، محور حرکت تقدیمی روی بردار تکانه زاویهای قرار میگیرد. در نتیجه و θ مقداری ثابت خواهد داشت.
در ادامه میخواهیم با استفاده از نتایج بالا، و را برحسب یکدیگر محاسبه کنیم. از آنجایی که زاویه θ همیشه ثابت است، تکانه زاویهای را میتوان به صورت زیر و در دستگاه مختصات xyz بیان کرد.
(رابطه 5)
از طرفی، روابط زیر را هم از قبل در اختیار داریم.
(رابطه ۶)
حال با مقایسه رابطههای ۵ و ۶ و با کمک روابط هندسی، معادلات زیر به دست میآیند.
حال با حل این سه معادله میتوانیم و را برحسب یکدیگر بیابیم.
تقدم یا انحراف در ژیروسکوپ
اگر تا به حال با ژیروسکوپهای اسباب بازی کار کرده باشید، میدانید که آنها میتوانند انواع ترفندهای جالب را انجام دهند. آنها میتوانند روی نخ یا یک انگشت تعادل داشته باشند. آنها میتوانند در حرکت حول محور چرخش به روشهای بسیار عجیب مقاومت کنند. اما جالب ترین اثر آنها تقدم یا انحراف نامیده میشود. این بخشی از ژیروسکوپ است که گویی گرانش را نقض میکند. ویدئوی زیر به شما تاثیرات استفاده از چرخ دوچرخه به عنوان ژیروسکوپ را نشان میدهد:
در ویدیو بالا یک چرخ دوچرخه از یک طناب آویزان شده است، شگفت انگیزترین بخش ویدیو بالا و همچنین چیزی که در مورد ژیروسکوپها باورنکردنی نیست، قسمتی است که چرخ دوچرخه ژیروسکوپی قادر است به شکل تصویر زیر در هوا باقی بماند.

چگونه این حالت توسط ژیروسکوپ انجام میشود؟
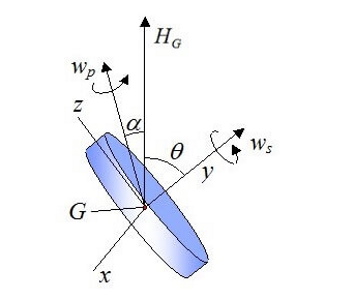
این اثر اسرار آمیز تقدم یا انحراف است. در حالت کلی precession به این صورت عمل میکند: اگر یک ژیروسکوپ در حال چرخش دارید و سعی میکنید محور چرخش آن را بچرخانید، ژیروسکوپ در عوض سعی میکند حول یک محور با زاویه راست نسبت به محور نیروی شما بچرخد. این موضوع در شکل زیر نمایش داده شده است.
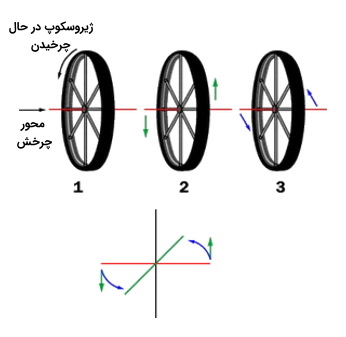
چرا انحراف یا تقدم در ژیروسکوپ رخ میدهد؟
چرا ژیروسکوپ باید این رفتار را نشان دهد؟ این کاملاً غیرمنطقی به نظر میرسد که محور چرخ دوچرخه میتواند چنین در هوا معلق باشد. اگر به آنچه در حال چرخش در قسمتهای مختلف ژیروسکوپ است توجه کنید خواهید دید که این رفتار کاملاً طبیعی است.
بیایید به دو بخش کوچک یعنی بالا و پایین ژیروسکوپ در حال چرخش نگاه کنیم. هنگامی که نیرو به محور وارد میشود، قسمت بالای ژیروسکوپ سعی میکند به سمت چپ حرکت کند و قسمت پایین ژیروسکوپ سعی میکند مانند تصویر به سمت راست حرکت کند. اگر ژیروسکوپ همان طور که در ویدئوی قبل نشان داده شده است نچرخد، چرخ سقوط میکند و در حالت عمودی قرار میگیرد. اگر ژیروسکوپ در حال چرخش باشد، باید قوانین فیزیکی زیر را در نظر گرفت.
اولین قانون حرکت نیوتن بیان میکند که جسمی که در حال حرکت است با سرعت ثابت در امتداد یک خط مستقیم به حرکت خود ادامه میدهد مگر اینکه تحت تأثیر نیروی نامتعادل قرار گیرد. بنابراین نقطه بالای ژیروسکوپ با نیروی وارد شده به محور عمل کرده و به سمت چپ حرکت میکند. به دلیل اولین قانون حرکت نیوتن این نقطه به حرکت به سمت چپ ادامه میدهد، اما چرخش ژیروسکوپ آن را میچرخاند.
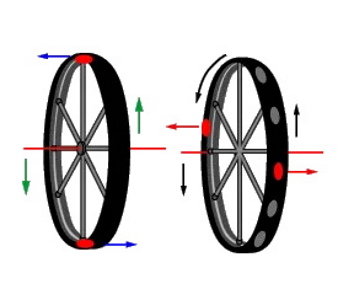
این تأثیر عامل انحراف یا تقدم است. در حقیقت بخشهای مختلف ژیروسکوپ نیروها را در یک نقطه دریافت میکنند اما پس از آن به موقعیتهای جدید چرخش انجام میدهند. هنگامی که بخش بالای ژیروسکوپ 90 درجه به پهلو میچرخد، به میل خود به حرکت به سمت چپ نیز ادامه میدهد. همین امر در مورد قسمت پایین ژیروسکوپ نیز صادق است. این نقطه 90 درجه به پهلو میچرخد و همچنان به حرکت خود به سمت راست ادامه میدهد. این نیروها چرخ را در جهت پیشروی میچرخانند. با ادامه چرخش به اندازه 90 درجه در نقاط مشخص شده، حرکت اصلی آنها لغو میشود. بنابراین محور ژیروسکوپ در هوا آویزان و در حال حرکت میماند. وقتی از این دریچه به حرکت ژیروسکوپ نگاه کنید، متوجه میشوید که این انحراف اصلاً شبیه به جادو و یا شعبده بازی نیست و کاملاً با قوانین فیزیک مطابقت دارد.
ژیروسکوپ برای چه مواردی استفاده میشود؟
ژیروسکوپها در قطب نمای کشتیها و هواپیماها، مکانیسم فرمان در اژدرها و سیستمهای هدایت کننده نصب شده در موشکهای بالستیک و ماهوارههای در حال چرخش در جاهای دیگر ساخته شدهاند.
چرا ژیروسکوپها تحت تاثیر جاذبه قرار نمیگیرند؟
ممکن است به نظر برسد که جاذبه بر روی آنها تاثیری ندارد، اما در حقیقت اینطور نیست. این اثر به دلیل اصل بقای تکانه زاویه ای است.
اثر ژیروسکوپی چیست؟
این اثر به روشی اشاره میکند که یک جسم دوار میخواهد محور چرخش خود را حفظ کند.
کاربردهای ژیروسکوپ در ابزارهای مختلف
ژیروسکوپها میتوانند اجسام بسیار گیج کنندهای باشند زیرا به روشهای عجیب و غریبی حرکت میکنند و حتی به نظر میرسد گرانش بر روی آنها تاثیری ندارد. این ویژگیهای خاص ژیروسکوپ را در همه چیز از دوچرخه تا سیستم ناوبری پیشرفته که در یک شاتل فضایی بسیار مهم کار میکند، میتوان مشاهده کرد. یک هواپیمای معمولی از دهها ژیروسکوپ، در همه چیز از قطب نما تا خلبان خودکار استفاده میکند. ایستگاه فضایی میر روسیه از 11 ژیروسکوپ برای حفظ جهت خود نسبت به خورشید استفاده کرده و تلسکوپ فضایی هابل نیز دستهای از ژیروسکوپهای ناوبری را در اختیار دارد. اثرات ژیروسکوپی در وسایل بازی مانند یو یو و فریزبی نیز نقش اساسی دارد.
تأثیر همه مواردی که در بالا بیان شد این است که هنگامی که یک ژیروسکوپ را بچرخانید، محور آن میخواهد همچنان در همان جهت ابتدایی باشد. اگر ژیروسکوپ را در مجموعهای از جیمبالها سوار کنید میتواند در همان جهت چرخش ابتدایی باقی بماند و این موضوع اساس کار یک قطب نمای ژیروسکوپی است.
اگر دو ژیروسکوپ که محورهای آنها در زاویه راست یکدیگر قرار دارند را پشت سر هم روی یک سکو نصب کنید و سکو را داخل مجموعهای از جیمبالها قرار دهید، سکو کاملاً سفت و محکم باقی میماند زیرا جیمبال ها به هر نحوی که میخواهند می چرخند. این اساس سیستمهای ناوبری اینرسی (INS) است.
در یک INS، سنسورهای موجود در محورهای جیمبال هنگام چرخش سکو را تشخیص میدهند. INS از این سیگنالها برای درک چرخش خودرو نسبت به سکو استفاده میکند. اگر مجموعهای از سه شتاب سنج حساس را به پلت فرم اضافه کنید، میتوانید دقیقاً مشخص کنید که خودرو به کدام سمت میرود و حرکت آن در هر سه جهت چگونه تغییر میکند. با این اطلاعات، خلبان خودکار هواپیما میتواند هواپیما را در مسیر خود نگه دارد و سیستم هدایت ماهواره میتواند ماهواره را در مدار مورد نظر قرار دهد.
ژیروسکوپ در ابزارهای مختلف چگونه مورد استفاده قرار میگیرد؟
- کاربرد ژیروسکوپ در یک استندیکم: در حین فیلمبرداری از صحنه تعقیب و گریز یک دوچرخه سوار سرعت در فیلم «بازگشت جدی» (Return of the Jedi) از یک استندیکم یا تثبیت کننده دوربین، به همراه دو ژیروسکوپ برای تثبیت بیشتر استفاده شد.
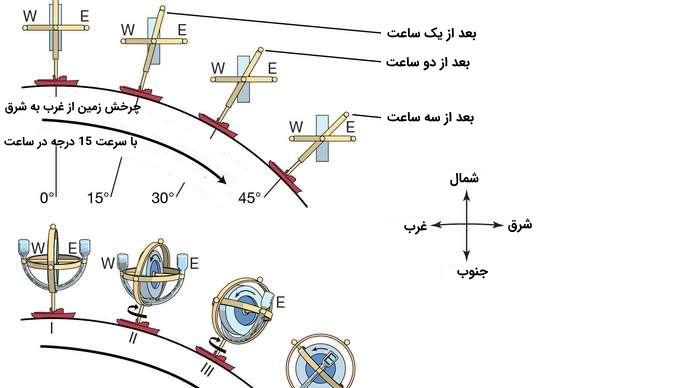
- کاربرد ژیروسکوپ در شاخص جهت یابی: ژیروسکوپها در شاخص جهت یابی استفاده میشوند که به عنوان ژیروس جهت دار نیز شناخته میشوند. شاخص جهت یابی وسیلهای برای پرواز است که در هواپیماها برای اطلاع خلبانان از مسیر و مسیر هواپیما استفاده میشود. نشانگر جهت یابی دارای یک محور چرخش است که به صورت افقی تنظیم شده و به سمت شمال اشاره میکند. اما برخلاف قطب نمای مغناطیسی، به دنبال شمال نیست. در هواپیمای مسافربری، نشانگر جهت یابی به آرامی از شمال دور میشود و باید در فواصل زمانی منظم جهت گیری مجدد انجام شود و از قطب نمای مغناطیسی به عنوان مرجع استفاده شود.
- کاربرد در قطب نمای ژیرو یا gyrocompass: ژیروسکوپ جهت دار که در بالا در مورد آن صحبت کردیم، ممکن است به دنبال شمال نباشد، اما یک قطب نمای ژیرو این کار را میکند. این کار با تشخیص چرخش زمین به دور محور خود و سپس جستجوی شمال واقعی به جای شمال مغناطیسی انجام میشود. معمولاً در این قطب نما یک میراگر داخلی برای جلوگیری از عبور بیش از حد هنگام کالیبراسیون مجدد از حرکت ناگهانی وجود دارد.
- کاربرد در شتاب سنج: از ژیروسکوپ در کنار شتاب سنجها نیز استفاده میشود که برای اندازه گیری شتاب مناسب مورد استفاده قرار میگیرند. در اینجا توجه به این نکته ضروری است که با اندازه گیری شتاب جسم و ادغام در طول زمان، میتوان به سرعت جسم رسید. با ادغام مجدد، میتوان موقعیت جسم را تعیین کرد. در حالی که یک شتاب سنج ساده شامل وزنی است که میتواند آزادانه به صورت افقی حرکت کند، یک طرح پیچیدهتر شامل یک ژیروسکوپ با وزن در یکی از محورها است.
- کاربرد ژیروسکوپ در ابزار الکترونیکی: با توجه به این واقعیت که ژیروسکوپ به محاسبه جهت و چرخش کمک میکند و برای حفظ جهت مرجع یا ایجاد ثبات در ناوبری مورد استفاده قرار میگیرد، طراحان آنها را در فناوری مدرن گنجاندهاند. امروزه ژیروسکوپ علاوه بر استفاده در قطب نما، هواپیما و دستگاههای اشاره گر رایانه در لوازم الکترونیکی مصرفی نیز استفاده میشود. در واقع بنیانگذار اپل، استیو جابز، اولین فردی بود که استفاده یا کاربرد ژیروسکوپ را در لوازم الکترونیکی مصرفی رواج داد. او این کار را با استفاده از ژیروسکوپ در گوشیهای آیفون انجام داد. از آن زمان، ژیروسکوپها معمولاً در تلفنهای هوشمند استفاده میشوند. علاوه بر این برخی از ویژگیهای تلفنهای اندروید مانند PhotoSphere یا 360 Camera and VR بدون سنسور ژیروسکوپ در تلفن به درستی کار نمیکنند. این حسگر ژیرو در تلفنهای هوشمند ما است که سرعت و شتاب زاویهای را حس و درک میکند. این المان همان چیزی است که به ما امکان میدهد با استفاده از حسگر حرکتی با تلفنها و تبلتهای خود بازی کنیم. به طور مشابه، ژیروسکوپ تلفن هوشمند به ما کمک میکند فیلمها یا عکسهای 360 درجه تماشا کنیم. وقتی تلفن خود را حرکت میدهیم، عکس یا فیلم به دلیل وجود یک ژیروسکوپ کوچک در گوشی حرکت میکند.
- کاربرد ژیروسکوپ در اسباب بازیها: ژیروسکوپها در اسباب بازیها نیز استفاده میشوند، در واقع ژیروسکوپهای اسباب بازی وجود دارند که ابزارهای آموزشی فوق العادهای را ایجاد میکنند زیرا به بچهها در درک نحوه عملکرد ژیروسکوپها کمک میکند.
- کاربرد ژیروسکوپ در دوچرخه: گفته میشود ژیروسکوپهای چرخ برقی که در چرخهای دوچرخه قرار داده شدهاند جایگزین مناسبی برای چرخهای کمکی در یادگیری دوچرخه سواری هستند.
- کاربرد ژیروسکوپ در کشتی های کروز: کشتیهای کروز از ژیروسکوپ برای تراز کردن وسایل حساس به حرکت مانند میزهای بیلیارد استفاده میکنند.
سنسور ژیروسکوپ در تلفن هوشمند شما چگونه کار میکند؟
ژیروسکوپ را میتوان دستگاهی دانست که برای حفظ جهت مرجع یا ایجاد ثبات در ناوبری، تثبیت کنندهها و غیره استفاده میشود. به طور مشابه، یک ژیروسکوپ یا یک حسگر ژیروسکوپ در تلفن هوشمند شما وجود دارد تا سرعت و شتاب چرخشی زاویهای را حس کند. به زبان ساده، همه بازیهای تلفن همراه که ما قادر به انجام آن در تلفنها، تبلتها و غیره هستیم به دلیل وجود سنسور ژیروسکوپ است. به طور مشابه، در تلفن هوشمند لازم است که بتوانید فیلم یا عکس 360 درجه تماشا کنید و به دلیل وجود ژیروسکوپ است که وقتی تلفن خود را حرکت میدهیم، عکس یا فیلم میچرخد و حرکت میکند.
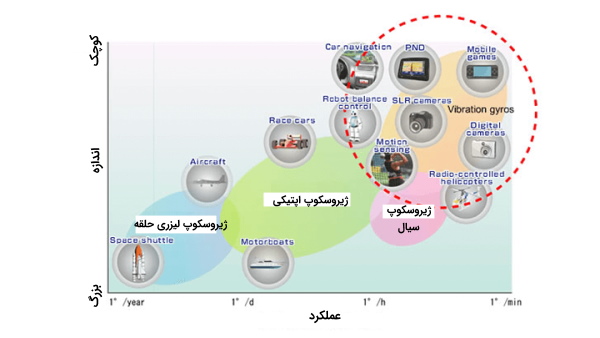
انواع سنسورهای ژیروسکوپ
سنسورهای ژیروسکوپ انواع و اقسام مختلفی و عملکرد و اندازههای متفاوتی دارند که در تصویر زیر میتوانید آنها را مشاهده کنید.
کاربردهای ژیروسکوپ در گوشیهای هوشمند
در ادامه برخی از کاربردهای ژیروسکوپ را در گوشیهای هوشمند بررسی و معرفی میکنیم.
رابط کاربری گرافیکی حسگر حرکت
ژیروسکوپ در تلفنهای هوشمند GUI ارائه میدهد که کاربر را قادر میسازد تا با کج کردن تلفن، منوها و اپلیکیشنها را انتخاب کند. برای بالا و پایین رفتن لیست مخاطبین، میتوانید تلفن را کمی کج کنید. این ویژگی یک تلفن هوشمند را قادر میسازد تا دستورات از پیش تعیین شده را بر اساس حرکات مختلف فعال کند. به عنوان مثال میتوانید تلفن را تکان دهید تا قفل شود.
پاسخ به تلفن و باز کردن یک صفحه
یک حسگر ژیروسکوپ در تلفن شما این امکان را دارد که به تلفن شما پاسخ دهد یا با دستوراتی مانند چرخاندن، تکان دادن آرام 2 تا 3 بار تلفن و غیره وب سایت یا صفحهای را باز کنید.
تثبیت کننده تصویر
تثبیت کننده تصویر یکی از کاربردهای ژیروسکوپ در تلفن هوشمند شما است و مانع از لرزش دست بر روی کیفیت تصویر میشود. این ویژگی تلفن را قادر میسازد تا در حین فشار دادن شاتر، تصاویر را ثبت کند تا به ثبت عکسهای واضحتر کمک کند. این اثر ارتعاشات و لرزشها را بر روی عکس و فیلم حذف میکند.
جهت یابی با GPS
در صورت از دست دادن سرویس یا شبکه، در تونلها یا جادههای زیرزمینی، GPS همچنان به جهت یابی خودرو با کمک ژیروسکوپ کمک میکند.
بازی با سنسور کنترل حرکت
اپل با عرضه آیفون 4 خود ژیروسکوپ را به هسته اصلی بازیهای متحرک تبدیل کرد. این ویژگی دولوپر برنامه را قادر میسازد تا بازی را از طریق تشخیص عمل کنترل کند و این امکان را به شما میدهد تا هنگام رانندگی با اتومبیل در بازی یا جت و غیره از تلفن خود به عنوان فرمان استفاده کنید. بازی گشتاوری را که به تلفن خود وارد میکنید تکرار میکند و از این رو بازیها را با سنسور حرکتی کنترل میکنید.
برخی برنامههای اندروید با سنسور ژیروسکوپ
برخی برنامههای اندروید که از حسگر ژیرو بهترین استفاده را میکنند به شرح زیر هستند:
- AndroSensor (+)
- Wifi Analyzer (+)
- کلینومتر (+)
- LightMeter Free (+)
- دماسنج هوشمند (+)
- صدا سنج (+)
- مانیتور ضربان قلب (+)
- مجموعه حسگر جعبه ابزار فیزیک (+)
برخی برنامههای آیفون با سنسور ژیروسکوپ
برنامه های آیفون که بهترین استفاده را از سنسور ژیروسکوپ میکنند نیز به شرح زیر هستند:
هر روز برنامه های بیشتری با استفاده از حسگرهای ژیرو به طور خلاقانه به بازار ارائه میشوند. همچنین نوآوریهای زیادی در فضای واقعیت مجازی با ژیروسکوپ در گوشیهای هوشمند انجام شده است. با این حال باید منتظر بود و دید که نسلهای بعدی تلفنهای هوشمند چه قابلیتهای جدیدی با استفاده از ژیروسکوپ به بازار ارائه خواهند داد.
بهترین گوشیهای هوشمند با سنسور ژیروسکوپ
با توجه به اینکه سنسور ژیروسکوپ امروزه بخشی اجتناب ناپذیر در هر تلفن هوشمندی است، برخی از بهترین تلفنهای هوشمندی که میتوانید با سنسور ژیروسکوپ تهیه کنید، در ادامه آمده است.
- آیفون X
- آیفون 8
- سامسونگ گلکسی 8
- LG V20
- سونی اکسپریا XZ
- گوگل پیکسل
- وان پلاس 5T
- هواوی آنر 8
- Moto G4
اطلاعات تکمیلی در مورد ژیروسکوپ
تا اینجا دانستیم اگر جسمی با سرعت زاویهای حول محور تقارن خود در حال چرخش باشد، محور چرخش و بردار تکانه زاویهای آن در یک راستا خواهند بود. حال ممکن است این جسم به طور موقت در معرض یک گشتاور خارجی قرار بگیرد. در این وضعیت، حرکت تقدیمی به چرخش اسپین اضافه میشود. از اینجا به بعد، محور حرکت تقدیمی بر بردار جدید تکانه زاویهای منطبق میشود. برای محاسبه حرکت جدید جسم، باید از معادلات حرکت اویلر استفاده کرد.
در حرکت بدون گشتاور، تنها نیروی خارجی وارد به جسم، نیروی وزن است که به مرکز جرم وارد میشود. وقتی صحبت از حرکت بدون گشتاور به میان میآید، به این دلیل است که هیچ گشتاوری وجود ندارد که قادر باشد جسم را حول مرکز جرمش (G) دوران دهد. در نتیجه، تکانه زاویهای حول مرکز جرم تغییر نخواهد کرد. برای درک بهتر موضوع، میتوان تصور کرد مرکز چرخش جسم در مرکز جرم آن قرار دارد.
معرفی فیلم آموزش مدل سازی و کنترل وضعیت فضاپیما با نرم افزار MATLAB
مجموعه فرادرس در تولید و تهیه محتوای آموزشی خود اقدام به تهیه فیلم آموزش مدل سازی و کنترل وضعیت فضاپیما با نرم افزار MATLAB کرده است. این مجموعه آموزشی از پنج درس تشکیل شده و برای دانشجویان رشته مهندسی هوافضا و مکانیک مفید است. پیشنیاز این درس آموزش سیستم های کنترل خطی و مجموعه آموزش های برنامه نویسی متلب (MATLAB) است.
درس اول این مجموعه مروری بر مفاهیم و کلیات مدلسازی و کنترل فضاپیما با متلب (MATLAB) دارد و درس دوم به دینامیک و سینماتیک وضعیت فضاپیما مانند مومنتوم، انرژی جنبشی دورانی، ماتریس ممان اینرسی، معادلات ممان اویلر و غیره میپردازد. در درس سوم روشهای مانور وضعیت در فضا معرفی و بررسی میشود این روشها شامل قانون فرمان کنترل با استفاده از خطاهای زوایای اویلر، قانون فرمان کنترلی با استفاده از ماتریس خطای کسینوس هادی، قانون فرمان کنترلی حول محور دوران اویلر و قانون فرمان کنترلی با استفاده از بردار خطای کواترنیون است.
درس چهارم به کنترل با وسایل تبادل مومنتوم اختصاص دارد و مباحثی مانند کنترل توسط وسایل تبادل مومنتوم، مدل وسیله تبادل مومنتوم، مدل ایده آل چرخ عکس العملی و غیره بررسی میشود. در نهایت و در درس پنجم شبیهسازی مثالهای کتاب انجام میشود که شامل طراحی کنترل مدرن برای کنترل وضعیت فضاپیما و طراحی کنترل LQR برای کنترل وضعیت فضاپیما است.
- برای دیدن فیلم آموزش مدل سازی و کنترل وضعیت فضاپیما با نرم افزار MATLAB + اینجا کلیک کنید.
جمعبندی
همانطور که دیدید ماهیت ژیروسکوپ، موضوعی پیچیده و نیازمند توجهی عمیق است. امیدواریم با مطالعه این مطلب، به درک مناسبی از عملکرد این اثر فیزیکی دست یافته باشید و این مطلب، انگیزهای برای یادگیری بیشتر مفاهیم ژیروسکوپ در شما ایجاد کرده باشد. در این مطلب در مورد دلیل رفتار ژیروسکوپ، انواع ژیروسکوپ، روابط ریاضی حاکم بر حرکت ژیروسکوپ و کاربردهای آن در زندگی روزمره صحبت کردیم.













سلام
ممنون از توضیحاتتون
تفاوت ژیروسکوپ ها با 3 حلقه و 2 حلقه و بدون حلقه مانند چرخ چیست؟
ژیرسکوپ
تلسکوپ
میکروسکوپ
پریسکوپ
همشون داداشن
دمتون گرم همش عالی بود
استادبانوی گرامی سپاس از شما🙏🏻
بسیار مفید و موثر بود.
لطفا چند مثال ساده و پیچیده در این مورد مکتوب کنید تا درک بهتری از حل مسائل داشته باشیم🌹
با سلام،
چرخهای دوچرخه، چرخش زمین در فضا و حتی رفتار بومرنگ از نمونه مثالهای ژیروسکوپ هستند.
با تشکر از همراهی شما با مجله فرادرس
تعادل دوچرخه ربطی به پدیده ژیروسکوپ نداره
بیشتر مربوط به اینرسی هست ، البته مبنای اصلی کار ژیروسکوپ هم اینرسی هست که از انحراف حلقه جلوگیری می کند.
فک میکنم مربوط به گریز از مرکز باشه
مطالب خیلی کامل و مناسب بووود
درود بر شما خانم دکتر داستان.
بسیار جامع و مفید بود. واقعا مشخص است با عشق و علاقه خیلی وقت گذاشتین برای ترجمه و نگارش این مطلب طولانی و کامل. از اینکه دانش و تجربیات خودتان را به اشتراک رایگان گذاشتین برای دیگران بسیار سپاسگذارم