ارتعاشات مکانیکی – بخش سوم: سیستم‌های دو درجه آزادی

در مطالب گذشته در مورد ارتعاشات آزاد و اجباری سیستم‌های یک درجه آزادی بحث کردیم. اما در واقعیت تمامی سیستم‌هایی که در اطراف خود می‌بینیم متشکل از بخش‌هایی هستند که از چندین درجه آزادی تشکیل شده‌اند. بنابراین بررسی این نوع از سیستم‌ها در واقعیت بسیار کاربردی خواهد بود. در نتیجه در ابتدا به معرفی مفهوم درجه آزادی و سپس به بررسی سیستم‌های دو درجه آزادی می‌پردازیم.

معادلات مربوط به یک سیستم دو درجه آزادی را می‌توان با استفاده از قانون دوم نیوتن و با استفاده از معادله اویلر لاگرانژ بدست آورد. در این مطلب تنها با استفاده از قانون دوم نیوتن معادلات حرکت را خواهیم یافت؛ اما در حالت کلی معادله اویلر لاگرانژ راه کوتاه‌تری را به ما نشان خواهد داد.

فیلم آموزش مکانیک تحلیلی ۱ مرور و حل مثال در فرادرس

کلیک کنید

درجه آزادی، عبارت است از تعداد مختصات مستقلی که برای توصیف یک سیستم نیاز است. به عنوان مثال، شکل زیر را در نظر بگیرید.

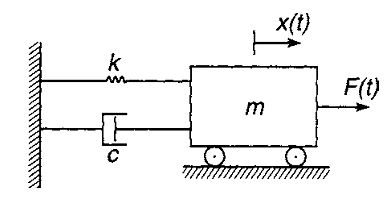
این سیستم از درجه 1 است، چراکه تنها با تعریف مختصاتی تحت عنوان x، می‌توان آن را توصیف کرد. حال سیستم شکل زیر را در نظر بگیرید.

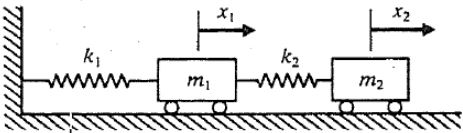
اگر در این سیستم فقط یک مختصات x تعریف کنیم، نمی‌توان با استفاده از آن موقعیت هر دو جرم 1 و 2 را نشان داد. تنها راه توصیف چنین سیستمی، تعریف دو مختصات x₁ و x₂ برای هر کدام از جرم‌ها است. در حالت کلی می‌توان درجه آزادی یک سیستم را با استفاده از روش زیر محاسبه کرد:

تعداد جرم‌های مستقل موجود در سیستم × تعداد حرکات ممکن برای هر جرم = درجه آزادی سیستم

توجه داشته باشید که منظور از جرم در عبارت بالا، بخش‌های مستقل از هم است. مثلا اگر دو جرم 1 و 2 به یکدیگر جوش داده شده باشند، یک جرم محسوب می‌شوند چرا که حرکت آن‌ها با هم صورت می‌گیرد.

به عنوان مثال در مورد تعداد درجات آزادی سیستم زیر فکر کنید.

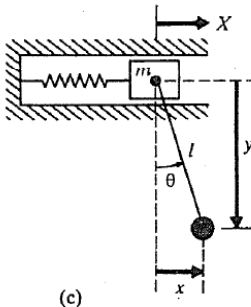
در این سیستم اگر جرم نوسان کننده در یک زاویه ثابت نگه داشته شود، همچنان می‌تواند به جرم ارتعاش کننده درون پیستون متصل بماند و سیستم کماکان توانایی ارتعاش کردن را خواهد داشت. بنابراین درجه آزادی این سیستم 2 است.

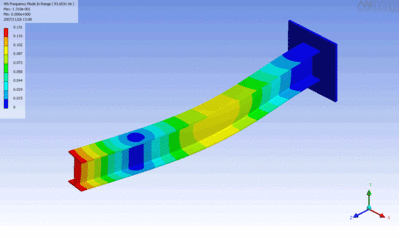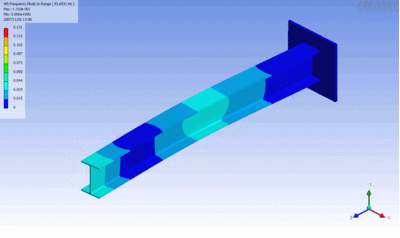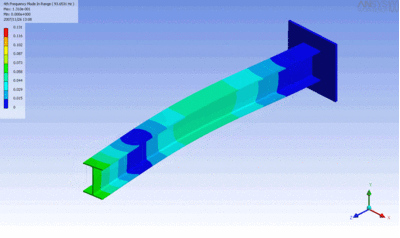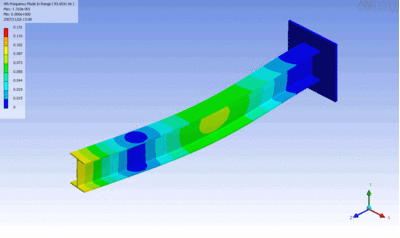
مبحث ارتعاشات چند درجه آزادی شاخه‌ای بسیار مهم و کاربردی از دینامیک است؛ چرا که امکان مدل‌سازی ارتعاش هر ماده الاستیکی را فراهم می‌کند. چنین سیستم‌هایی به‌صورت چندیدن جرم و فنر در نظر گرفته می‌شوند که به‌شکلی پیوسته به یکدیگر متصل شده و در ترکیبی از مود‌های نوسانی خود، ارتعاش می‌کنند. انیمیشن زیر تیری را نشان می‌دهد که در یکی از مود‌های ارتعاشی خود نوسان می‎کند. تنش‌های ایجاد شده در این تیر در هر لحظه با استفاده از نرم‌افزار «انسیس» مدل‌سازی شده است.

سیستم‌های با درجه آزادی 2

در یک سیستم با درجه آزادی n، همین تعداد معادله نیز وجود خواهد داشت. بنابراین در یک سیستم دو درجه آزادی، دو معادله به منظور بررسی ارتعاشی مجموعه نیاز است (برای هر جرم، یک معادله). این معادلات با یکدیگر در ارتباط هستند، به نحوی که تمامی مختصات تعریف شده در همه معادلات ظاهر خواهند شد. اگر پاسخی هارمونیک برای سیستم در نظر بگیریم، به دو معادله می‌رسیم که دو فرکانس طبیعی به ما می‌دهند.

همان‌طور که در بخش‌های قبل نیز بیان شد اگر به سیستم، تحریک اولیه‌ای وارد شود، مجموعه در یکی از فرکانس‌های طبیعی خود نوسان خواهد کرد. در این حالت دامنه‌های نوسان (دو مختصات تعریف شده)، با یکدیگر در ارتباط خواهند بود. به حالت‌های مختلف این نوسانات، «مود‌های طبیعی نوسان» (Natural Mode of Vibration)، «مود نرمال» (Normal Mode) یا «مود اصلی» (Principle mode) گفته می‌شود.

بنابراین یک سیستم دو درجه آزادی از دو مود نوسانی تشکیل شده که به دو فرکانس طبیعیش مرتبط است. از همین رو اگر به یک سیستم دو درجه آزادی، تحریکی اعمال کنیم، پاسخ آن حاصل جمع مود‌های نرمالش است؛ اما اگر این سیستم با استفاده از تحریک هارمونیک خارجی (نوسان اجباری) مرتعش شود، فرکانس ارتعاش مجموعه همان فرکانس تحریک خواهد بود.

معادلات حرکت برای سیستم دو درجه آزادی در حالت ارتعاش اجباری

در این قسمت قصد داریم تا در مورد سیستم جرم-فنر-دمپر دو درجه آزادی صحبت کنیم که تحت یک نیروی هارمونیک به ارتعاش در آمده است.

فیلم آموزش مکانیک تحلیلی ۲ (حل تست کنکور کارشناسی ارشد) (رایگان) در فرادرس

کلیک کنید

هما‌ن‌طور که در بالا نیز بیان شد، برای توصیف یک سیستم چند درجه آزادی، در ابتدا بایستی مختصات توصیف کننده سیستم را تعریف کنیم. بدین منظور شکل - یا همان سیستم - زیر را در نظر بگیرید.

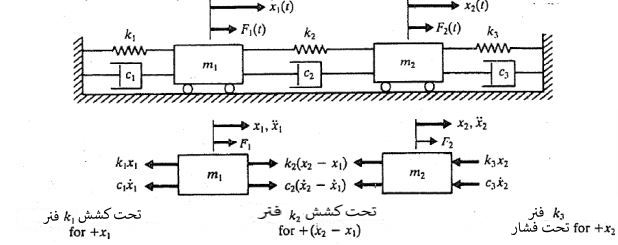
شکل بالا سیستمی دو درجه آزادی به همراه نیروهای وارد شده به آن را نشان می‌دهد. در این سیستم از دو مختصات (x₁(t و (x₂(t به منظور توصیف مکان جرم‌های m₁ و m₂ استفاده شده. بنابراین تنها با نشان دادن مکان این دو جرم، ارتعاش سیستم مفروض قابل بیان خواهد بود.

به منظور بررسی کلی سیستم، فرض کنید دو نیروی متغیر F₁ و F₂ نیز به این دو جرم وارد می‌شوند. حال با پیاده‌سازی قانون دوم نیوتن برای جرم‌های m₁ و m₂، می‌توان نوشت:

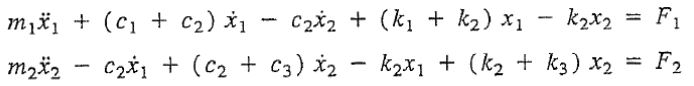
همان‌گونه که بیان شد هر دو مختصات تعریف شده در هر دو معادله ظاهر شده‌اند. بنابراین این دو رابطه، معادلات دیفرانسیلی از مرتبه دوم هستند که با یکدیگر کوپل شده‌اند. در نتیجه می‌توان انتظار داشت که حرکت هر کدام از جرم‌ها، روی دیگری تاثیرگذار باشد. توجه داشته باشید که در تحلیل سیستم‌های چند درجه آزادی تلاش می‌شود تا معادلات به‌شکل ماتریسی نوشته و نهایتا با استفاده از رایانه حل شوند؛ بنابراین معادلات مربوط به این سیستم را به‌صورت زیر بیان می‎کنیم.

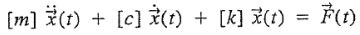
در این معادله، [c]، [m] و [k] به‌ترتیب ماتریس جرم، میرایی و سختی هستند. (x(t و (F(t نیز بردارهای جابجایی و نیرو را نشان می‌دهند. این ماتریس‌ها و بردارها به‌شکل زیر نوشته می‌شوند.

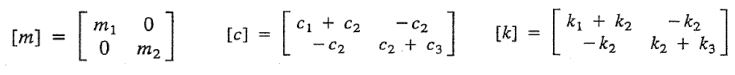
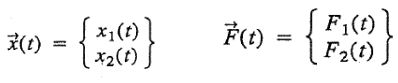
مطابق با فرمول‌های بالا ماتریس‌های [c]، [m] و [k] همگی 2×2 هستند؛ هم‌چنین عناصر تشکیل‌ دهنده آن‌ها از جرم‌ها، ضرایب میرایی و ضرایب سختی تشکیل شده‌اند. توجه داشته باشید که تمامی ماتریس‌های ذکر شده، متقارن هستند. بنابراین می‌توان گفت:

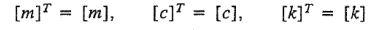
البته می‌توانید با استفاده از معادله اویلر لاگرانژ نیز به همین معادلات دست یابید.

ارتعاش آزاد سیستم دو درجه آزادی بدون میرایی

به منظور بررسی کلی یک سیستم دو درجه آزادی (ارتعاشِ اجباریِ میرا) در ابتدا بهتر است تا سیستمی را بررسی کنیم که نیرویی هارمونیک به آن وارد نشود و ‌هم‌چنین میرا نباشد. بدین منظور در این قسمت قصد داریم تا ارتعاش آزاد یک سیستم دو درجه آزادی نامیرا را مورد بررسی قرار دهیم.

در ابتدا برای بررسی یک سیستم نامیرای دو درجه آزادی، بردار (F(t و ماتریس [c] را برابر با صفر قرار می‌دهیم؛ در نتیجه معادله کلی سیستم مفروض به‌صورت زیر خواهد شد.

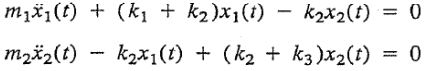
همان‌طور که در قسمت معادلات دیفرانسیل نیز ذکر کردیم، پاسخ معادله را به‌صورت هارمونیک در نظر می‌گیریم. بنابراین (x₁(t و (x₂(t را می‌توان در قالب زیر در نظر گرفت.

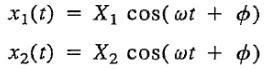
در این دو فرض، مقادیر X₁ و X₂ و Φ به‌ترتیب دامنه نوسان (x₁(t و (x₂(t و اختلاف فاز هستند. با جایگذاری دو پاسخ فرض شده بالا در معادلات دیفرانسیل بدست آمده، عبارات زیر حاصل خواهند شد.

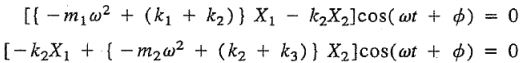
از آنجایی که معادلات بیان شده بایستی در تمامی زمان‌های t صادق باشند، بنابراین عبارات درون براکت، برابر با صفر قرار داده می‌شوند. در نتیجه خواهیم داشت.

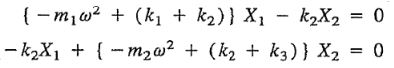
بدیهی است که پاسخ X₁ و X₂ برابر با صفر، در این معادلات صادق خواهد بود، اما این پاسخ‌ها، سیستم را در حالتی نشان می‌دهد که ارتعاشی انجام نمی‌دهد؛ بنابراین بایستی پاسخ دیگر این دو معادله را پیدا کنیم. به‌منظور یافتن دو پاسخ معادله مفروض، دترمینان ضرایب آن‌ها را برابر با صفر قرار می‌دهیم؛ در نتیجه می‌توان نوشت.

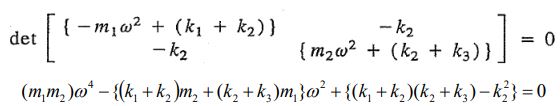
معادله بالا، تحت عنوان «معادله مشخصه» (Characteristic Equation) شناخته می‌شود؛ دلیل این نامگذاری، مشخص شدن فرکانس‌های نوسان با استفاده از این معادلات است. ریشه‌های معادله مشخصه برابر هستند با:

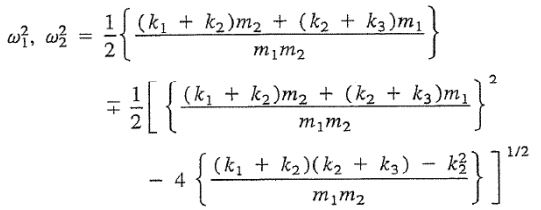
بنابراین می‌توان گفت برای سیستم مفروض، پاسخی به‌شکل زیر وجود دارد.

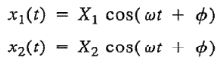
در این معادلات مقادیر ω₁ و ω₂ برابر با مقادیر زیر در نظر گرفته می‌شوند.

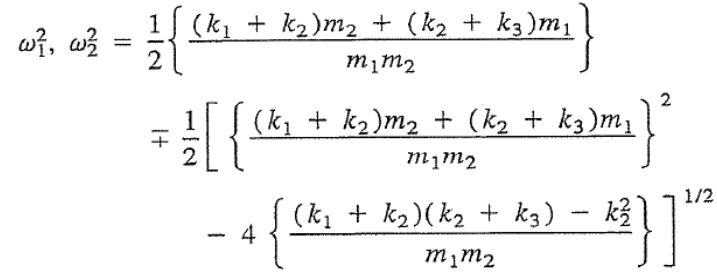
توجه داشته باشید که مقادیر X₁ و X₂ مرتبط با ω₁، به وسیله X⁽¹⁾₁ و X⁽¹⁾₂ نشان داده می‌شوند؛ هم‌چنین دامنه‌های X₁ و X₂ مرتبط با ω₂ را با X⁽²⁾₁ و X⁽²⁾₂ بیان می‌کنند. معادلات بالا همگن هستند. به‌منظور تحلیل پاسخ چنین سیستمی تعاریف زیر صورت می‌گیرد.

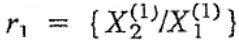
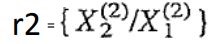
مقادیر r=r₁ و r=r₂ را می‌توان بر حسب فرکانس‌های ω=ω₁ و ω=ω₂، به‌شکل زیر بیان کرد.

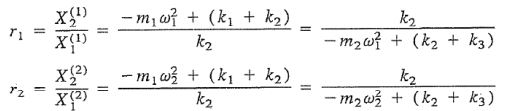
مودهای نرمال مرتبط با ω₁² و ω₂² را می‌توان به‌ترتیب زیر بیان کرد.

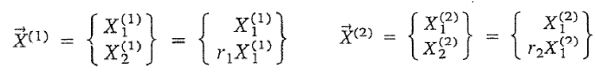
₁$$\overrightarrow{X}$$ و ₂$$\overrightarrow{X}$$ تحت عنوان «شکل مودی» (Mode Shape) جابجایی جرم‌های موجود در سیستم شناخته می‌شوند. با استفاده از فرکانس‌های طبیعی و دامنه‌های بدست آمده، پاسخ سیستم را می‌توان به‌صورت زیر بیان کرد.

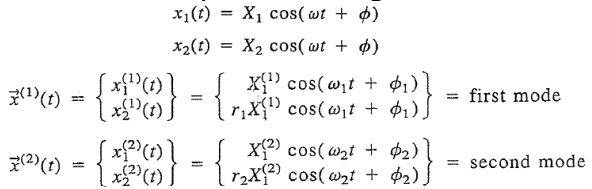
توجه داشته باشید که در این معادلات، مقادیر X⁽¹⁾₁ ،X⁽²⁾₁ ،Φ₁ و Φ₂ با استفاده از شرایط اولیه بدست ‌می‌آیند.

شرایط اولیه

دو معادله مربوط به سیستم دو درجه آزادی که در زیر بیان شده، از مرتبه دوم هستند؛ بنابراین برای هر کدام از جرم‌ها به دو شرط اولیه نیاز داریم.

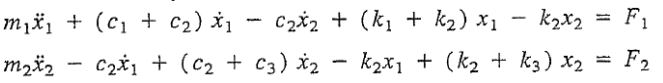
لازم به ذکر است که به منظور بررسی یک سیستم چند درجه آزادی در ابتدا بایستی مشخص کرده باشیم که سیستم در کدام مود خود در حال ارتعاش است. این‌که سیستم در کدام مود، ارتعاش می‌کند به نوع تحریک اولیه وابسته است، اما بایستی بدانید که در حالت کلی چنین سیستمی در ترکیبی از مودهای نوسانی خود به ارتعاش در می‌آید. بنابراین همواره پاسخ ارتعاشی به صورت ترکیبی از دو مود ارتعاشی ((x₁(t و (x₂(t) در نظر گرفته می‌شود.

بنابراین فرض کنید پاسخ کلی سیستم به‌شکل زیر در نظر گرفته شده.

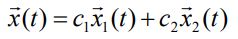
از آنجایی که پاسخ‌های (x₁(t و (x₂(t شامل ثابت‌های X هستند، بنابراین ضرایب c را برابر با 1 فرض می‌کنیم. حال می‌توانیم پاسخ‌های (x₁(t و (x₂(t را به‌صورت زیر بیان کنیم.

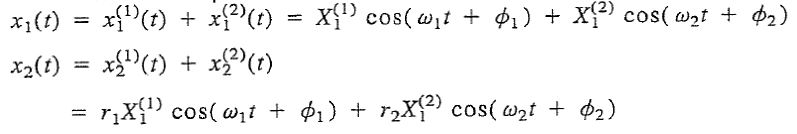
در این معادلات، ثابت‌های X⁽¹⁾₁ ،X⁽²⁾₁ ،Φ₁ و Φ₂ با استفاده از شرایط اولیه بدست می‌آیند. در حالت کلی این شرایط را به‌شکل زیر بیان می‌کنیم.

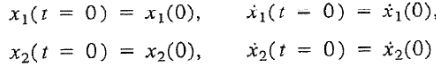
با جایگذاری شرایط اولیه در پاسخ‌های ارتعاشی در نظر گرفته شده، داریم:

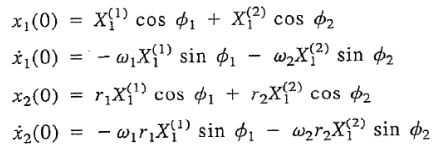
روابط بالا، چهار معادله هستند که با حل آن‌ها 4 مجهولِ X⁽¹⁾₁ ،X⁽²⁾₁ ،Φ₁ و Φ₂ بدست می‌آیند. پس از حل این معادلات مجهولات مدنظر به‌شکل زیر محاسبه می‌شوند. [توجه داشته باشید که در این معادلات، r₁ و r₂ جزو معلومات هستند]

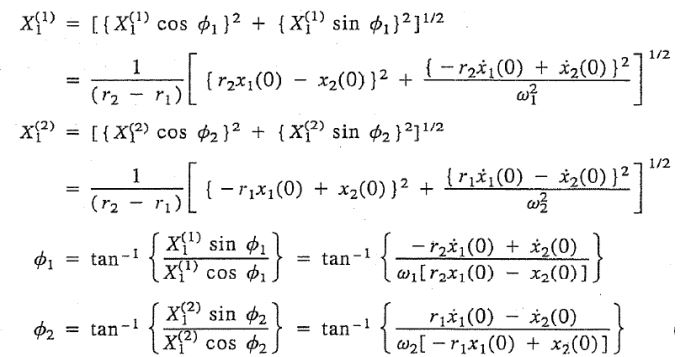
بنابراین پاسخ نهایی ارتعاش این سیستم دو درجه آزادی، با فرض معلوم بودن تحریک اولیه (شرایط اولیه) محاسبه شد.

فرکانس‌های طبیعی سیستم جرم و فنر

به منظور درک بهتر مطالب عنوان شده در بالا، مثال زیر را مورد بررسی قرار می‌دهیم.

فیلم آموزش مکانیک تحلیلی ۲ – جامع و کاربردی در فرادرس

کلیک کنید

مثال: فرکانس‌های طبیعی و مود‌های نوسانی سیستمی را بیابید که مطابق شکل زیر در راستای عمودی نوسان می‌کند.

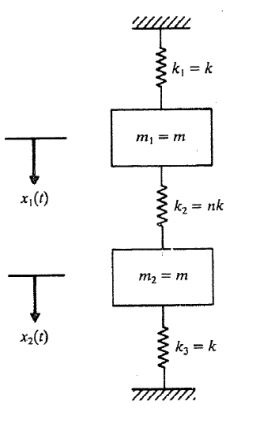
حل: با تعریف مختصات‌های x₁ و x₂ به عنوان مکان جرم m₁ و m₂، قانون دوم نیوتن برای این سیستم به‌شکل زیر است.

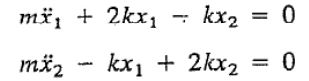
بنابراین با فرض پاسخی هارمونیک برای این معادلات، داریم.

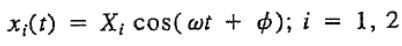
در نتیجه دترمینان ضرایب این معادله به‌شکل زیر خواهد بود.

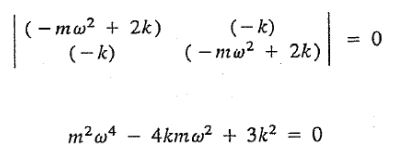
پاسخ معادله بالا، فرکانس‌های طبیعی سیستم هستند.

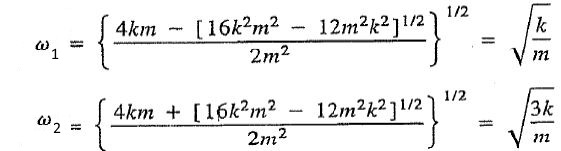
با جایگذاری جرم‌ها و سختی‌های ارائه شده در این مثال، در فرمول زیر، ضرایب r₁ و r₂ تعیین می‌شوند.

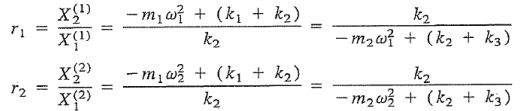
در نتیجه:

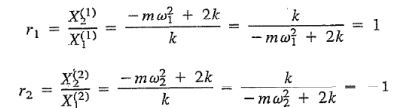
با قرار دادن ضرایب بدست آمده در معادلات زیر می‌توان مود اول و دوم این ارتعاش را به‌شکل زیر بدست آورد.

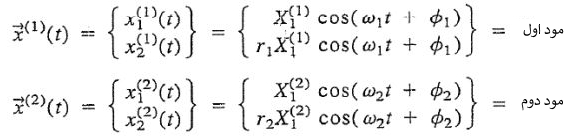
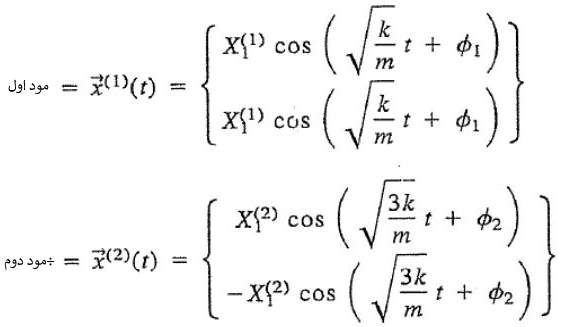
توجه داشته باشید که نوسان یک سیستم در مود‌های طبیعی به این معنا است که تحریک اولیه به نحوی صورت می‌گیرد که سیستم یا در مود x₁ و یا در x₂ نوسان می‌کند. برای نمونه در این مثال، سیستم دو مود ارتعاشی دارد. اگر در مود x₁ نوسان کند، دو جرم با همدیگر و شبیه به یک جسم صلب نوسان خواهند کرد. در شکل زیر ارتعاش سیستم در مود اول ارتعاشیش را می‌بینید.

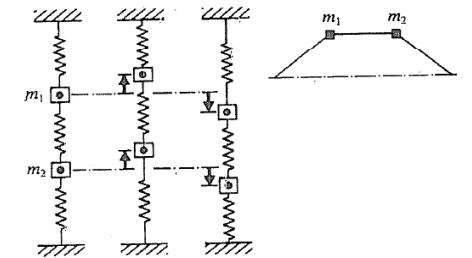
مطابق با شکل زیر اگر این سیستم در مود x₂ نوسان کند، دو جرم در خلاف جهت یکدیگر ارتعاش خواهند کرد.

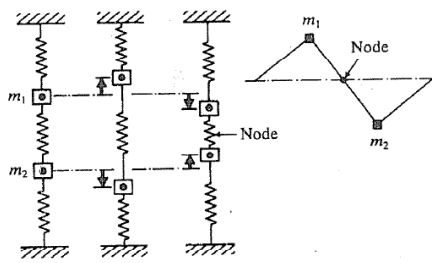
انیمیشن‌های زیر دو مود نوسانی سیستمی مشابه را نشان می‌دهند که در حالت افقی قرار گرفته.

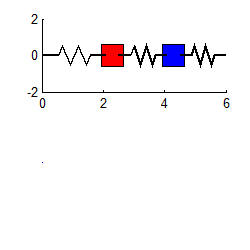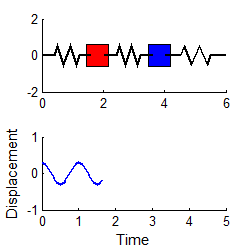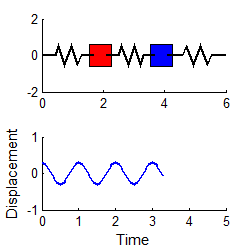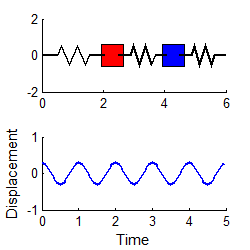
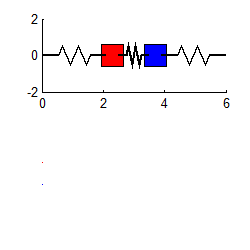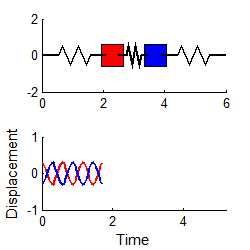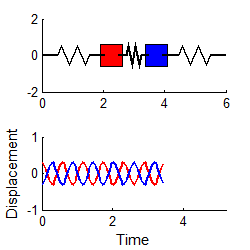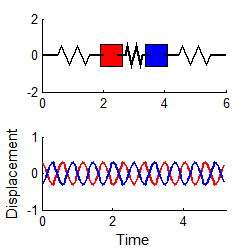
نهایتا با استفاده از معادله زیر که قبلا نیز بیان شد و جایگذاری مود‌های ارتعاشی در آن، می‌توان پاسخ نهایی را برای (x₁(t و (x₂(t به شکل زیر بدست آورد.

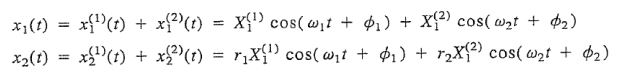
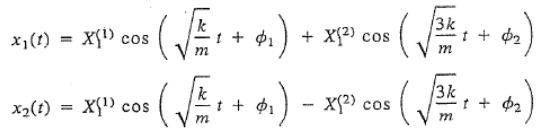
توجه داشته باشید که دامنه نوسان (X) و اختلاف فاز (Φ) مقادیری هستند که در صورت معلوم بودن شرایط اولیه، بدست خواهند آمد.

اگر به مباحث مرتبط در زمینه دینامیک و ارتعاشات علاقه‌مند هستید، احتمالا آموزش‌های زیر برای شما مفید خواهند بود.

• ارتعاشات مکانیکی — بخش اول: اصول و مفاهیم
• مجموعه آموزش‌های متلب و سیمیولینک
• ارتعاشات مکانیکی — بخش دوم: ارتعاشات اجباری
• مجموعه آموزش‌ نرم‌افزارهای مهندسی مکانیک

^^