حرکت پرتابی – به زبان ساده

به حرکتی که در آن یک جسم فقط تحت تاثیر نیروی گرانش، مسیرش تعیین شود، حرکت پرتابی گفته می‌شود. جسم پرتاب شده را «پرتابه» می‌نامند. با صرف نظر کردن از نیروی اصطکاک هوا، پرتاب دیسک، موشک (در مسیری طولانی) و حتی شوت کردن توپ فوتبال، نمونه‌هایی از این نوع حرکت محسوب می‌شوند. این حرکت در حقیقت با استفاده از رابطه‌ای درجه ۲ توصیف می‌شود. نحوه بدست آمدن این رابطه و محاسبات مربوط به آن در ادامه این مطلب بیان خواهد شد.

مهم‌ترین نکته در تحلیل حرکت پرتابی (و هر حرکتی که ناشی از شتاب باشد) این است که می‌توان مسیر حرکت جسم را به صورت جدا، در دو محور متخصات عمود بر هم بررسی کرد. در حالت کلی می‌توان حرکت‌های پرتابی مختلفی را تحلیل کرد. برای نمونه پرتاب یک توپ فوتبال به صورت عمودی نوعی حرکت پرتابی محسوب می‌شود. هم‌چنین زمانی که همان توپ را شوت کنید، مسیری پرتابی را طی خواهد کرد. توجه داشته باشید که در این مطلب فقط تاثیر نیروی گرانش روی اجسام در نظر گرفته شده و از انواع دیگر نیروها همچون نیروهای آیرودینامیکی صرف نظر شده است.

همان‌طور که در بالا نیز بیان شد، در یک حرکت پرتابی تنها نیروی فرض شده، گرانش است. برای درک بهتر، شکل زیر را در نظر بگیرید. در این شکل مولفه‌های سرعت یک جسم در دو جهت عمود بر هم و هم‌چنین مسیر حرکت آن مشخص شده‌اند.

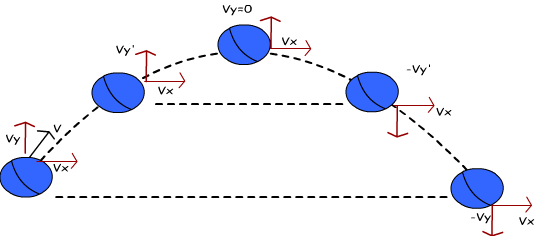
همانطور که در شکل بالا نیز می‌بینید، در موقعیت‌های مختلف، بردارهای سرعت در جهت‌ محورهای مختصات دارای اندازه‌های متغیری هستند. در حالت اولیه سرعت جسم برابر با V و در جهت شمال شرقی است. از آنجایی که تنها نیروی وارد شده به جسم، نیروی گرانش در نظر گفته شده، بنابراین سرعت جسم فقط در راستای y تغییر می‌کند و اندازه سرعت در جهت x ثابت است. توجه داشته باشید که محور x و  y به نحوی در نظر گرفته شده‌اند که محور ‌y هم‌راستا با نیروی گرانشی و x عمود بر آن است.

سرعت V_y (مولفه سرعت در راستای محور y) در ابتدا و به دلیل حضور نیروی گرانشی کاهش می‌یابد. پس از آن در بیشترین ارتفاع، سرعت جسم به صفر می‌رسد و دوباره نیروی گرانش سرعت آن را افزایش می‌دهد. تحلیل سرعت در راستای y دقیقا همانند وضعیتی است که در آن یک جسم به صورت عمودی پرتاب شود. فقط تفاوت در این است که در حالت پرتاب عمودی، همواره سرعت در راستای x صفر است.

برای تشریح حرکت پرتابی شکل بالا، فرض کنید که در حالت اولیه جسمی با سرعت اولیه V و در جهت شمال شرقی پرتاب می‌شود. V_x و V_y مولفه‌های سرعت در جهات x و y هستند. برای تحلیل این مسئله حرکات در دو جهت عمود بر هم را به صورت جدا در نظر می‌گیریم.

معادلات حرکت در حالت کلی

قبل از هرچیز بهتر است تا در مورد کلیاتِ معادلات حرکت صحبت کنیم. از این رو جسمی را فرض کنید که در مکان اولیه  x₀ قرار گرفته و سرعت اولیه آن برابر با V₀ است. در این صورت می‌توان مکان و سرعت لحظه‌ای این جسم را با استفاده از معادلات زیر بدست آورد.

فیلم آموزش فیزیک پایه ۱ – مفاهیم پایه + حل مثال در فرادرس

کلیک کنید

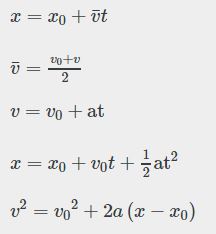
حال می‌توان با استفاده از معادلات بالا حرکت پرتابی یک جسم را به صورت مجزا و در راستاهای x و y توصیف کرد.

توصیف مسیر توپ

به‌منظور بررسی حرکت پرتابی، فرض کنید مطابق با شکل زیر، فوتبالیستی یک توپ را با سرعت اولیه V₀ و زاویه θ شوت می‌کند. توجه کنید که در این تحلیل، از نیرو‌های اصطکاک وارد شده به توپ صرف نظر شده.

فیلم آموزش شبیه سازی حرکت یک پرتابه در سیمیولینک با در نظر گرفتن اثر مقاومت هوا (رایگان) در فرادرس

کلیک کنید

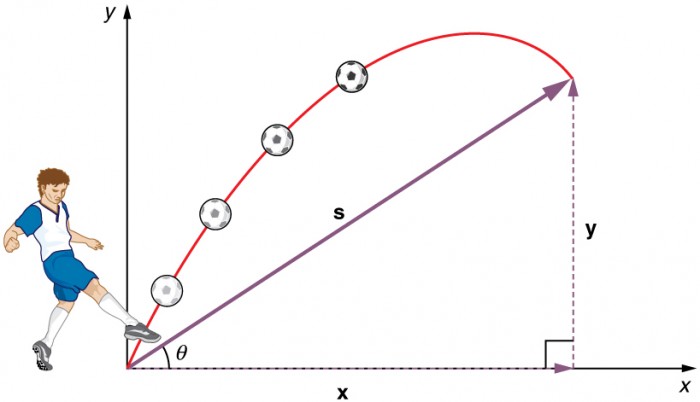
قدم اول

برای بررسی این حرکت، در ابتدا بایستی دو محور مختصات عمود به هم در نظر گرفت. برای راحتی حل مسئله بهتر است که یکی از این محور‌ها در راستای شتاب گرانشی باشد. دلیل این کار حذف کردن شتاب از معادلات مربوط به حرکت در راستای افقی است.

بنابراین محور‌های x و y را مطابق با شکل بالا در نظر می‌گیریم. توجه داشته باشید که سرعت اولیه نیز بایستی در راستاهای x و y تجزیه شوند. بنابراین سرعت اولیه در راستای محور x برابر است با:

$$V_{0x}=V_0cos(\theta)$$

از آنجایی که شتابی در راستای محور x به توپ وارد نمی‌شود، بنابراین سرعت آن نیز در این راستا ثابت است. از این رو سرعت توپ در هر لحظه همان سرعت اولیه خواهد بود. بنابراین می‌توان معادله سرعت در راستای محور x را به صورت زیر بیان کرد:

$$V_{x}(t)=V_0cos(\theta)$$

با توجه به سرعت بدست آمده، مختصات x جسم در هر لحظه، به شکل زیر قابل نوشتن است.

$$x(t)=V_0tcos(\theta)$$

قدم دوم

همانند مرحله قبل در این قدم نیز شتاب‌ (g-)، سرعت اولیه (V_0y) و جابجایی اولیه در راستای y را در معادلات حرکت جایگزین می‌کنیم. بنابراین جابجایی و سرعت توپ در راستای y به صورت زیر محاسبه می‌شوند. توجه داشته باشید که سرعت اولیه در راستای y را می‌توان با تصویر کردن V₀ در راستای محور y، به صورت زیر بدست آورد.

$$V_{y}(t)=V_0sin(\theta)$$

بنابراین جابجایی در هر لحظه برابر است با:

$$y(t)=-{1 \over 2} {gt^2}+V_0tsin{\theta}$$

دلیل علامت منفی این است که شتاب گرانشی خلاف جهت y است.

قدم سوم

در قدم اول، توابع جابجایی x و y نسبت به زمان محاسبه شدند. با استفاده از از این معادلات می‌توان مسیر حرکت جسم را در زمان پیش‌بینی کرد. برای توصیف مسیر حرکت در دستگاه مختصات x-y بایستی وابستگی x و y را نسبت به یکدیگر بیابیم. از این رو با استفاده از دو معادله (x(t و (y(t و حذف t از آن‌ها می‌توان مسیر حرکت جسم را در دو بعد یافت.

برای این منظور در ابتدا معادله (x(t را بر حسب t مرتب می‌کنیم. بنابراین می‌توان رابطه x(t)=v₀cosθ×t را به شکل زیر بازنویسی کرد.

$$t={x(t) \over {V_0cos{ \theta}}}$$

با جایگذاری معادله بالا در رابطه (y(t داریم.

$$y(t)=-{1 \over 2} {gt^2}+V_0tsin{\theta}=-{1 \over 2} {g({x \over {v_0cos {\theta}}})^2}+V_0({x \over {V_0cos{\theta}}})sin{\theta}$$

با مرتب کردن معادله بالا و جایگذاری ۹.۸ به جای g، شکل نهایی مسیر x-y به صورت زیر بدست می‌آید.

$$y={-gx^2\over2V_0^2cos^2(\theta)}+xtan(\theta)$$

در رابطه بالا فقط x و y  متغیر هستند و بقیه ضرایب اعداد ثابت‌اند؛ بنابراین می‌توان گفت که شکل معادله به صورت سهمی مرتبه دوم است.

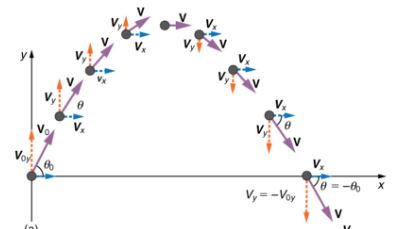
شکل بالا مسیر پرتابی توپ و هم‌چنین اندازه‌ سرعت آن را در هر لحظه نشان می‌دهد. توجه داشته باشید که سرعت لحظه‌ای جسم را می‌توان به استفاده از فرمول زیر محاسبه کرد.

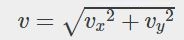
بدیهی است که در حرکت پرتابی تمامی معادلات حرکت صادق هستند. برای نمونه می‌دانیم که اگر جسمی تحت تاثیر شتاب a سرعتش از V₀ به V تغییر کند، می‌توان رابطه بین سرعت اولیه و نهایی آن با شتاب را به صورت زیر بیان کرد:

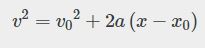
بنابراین قادریم تا از معادله بالا در حرکت پرتابی نیز استفاده کنیم. مثلا با جایگذاری سرعت اولیه و نهایی در راستای y، رابطه زیر به‌منظور توصیف جابجایی صورت گرفته در این راستا قابل بیان است.

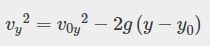
مثال ۱

مطابق با شکل زیر، در یک مراسم آتش‌بازی، فشفشه‌ای با سرعت اولیه ۷۰ متر بر ثانیه و با زاویه ۷۵ درجه نسبت به محور x پرتاب می‌شود.

تصور کنید که این فشفشه هنگام رسیدن به بیشترین ارتفاعش منفجر می‌شود. با صرف نظر کردن از مقاومت هوا موارد زیر مطلوب است.

1. ارتفاعی که فشفشه در آن منفجر می‌شود چقدر است؟
2. این فشفشه چند ثانیه پس از پرتاب منفجر می‌شود؟
3. مسافت افقی پیموده شده در زمان انفجار چقدر است؟

با توجه به این که تنها نیروی گرانشی است که به جسم وارد می‌شود و از مقاومت هوا نیز صرف نظر شده، بنابراین حرکت مفروض، پرتابی در نظر گرفته می‌شود.

اولین قدم این است که حرکات در راستای محورهای عمودی و افقی را به صورت جداگانه تحلیل کنیم. از آنجایی که شتابی در راستای x به جسم وارد نمی‌شود، می‌توان گفت:

a_x=0

a_y= –g

هم‌چنین می‌توان مبدا دستگاه مختصات را نقطه پرتاب در نظر گرفت، در نتیجه مقادیر x₀=0 و y₀=0 صفر در نظر گرفته می‌شوند.

برای پاسخ به قسمت ۱، بایستی سرعت اولیه در راستای y را بدست آوریم. این سرعت برابر است با:

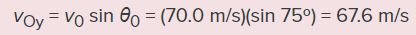
از طرفی فشفشه در بیشترین ارتفاعش منفجر می‌شود. همان‌طور که در بالا نیز بیان کردیم، در بیشترین ارتفاع، سرعت در راستای y برابر با صفر است. از این رو با جایگذاری سرعت بالا در رابطه $$V_y^2-V_0^2=-2g(y-y_0)$$ می‌توان ارتفاع انفجار را به صورت زیر بدست آورد.

$$V_y^2-V_0^2=-2g(y-y_0)\rightarrow \enspace 0^2-67.6^2=-2×9.8(y-0)$$

با حل معادله بالا مقدار y برابر با ۲۳۳ متر بدست می‌آید.

در قسمت ۱، مسئله زمان مطرح نبود، به همین دلیل از معادله‌ای استفاده کردیم که در آن t وجود نداشته باشد. در قسمت ۲ از ما زمان منفجر شدن خواسته شده. بنابراین بایستی از معادله‌ای استفاده کنیم که بر خلاف قسمت اول در آن t وجود داشته باشد. با توجه به این‌که سرعت جسم در لحظه‌ انفجار، صفر است، می‌توان از معادله سرعت لحظه‌ای در راستای y استفاده کرد. در نتیجه داریم:

$$V_y(t)=V_0-9.8t  \buildrel _V=0 \over \longrightarrow 9.8t=V_0\rightarrow \enspace t={67.6 \over 9.8}=6.90<br /> s$$

اگر زمان انفجار بدست آمده را در معادله مربوط به جابجایی افقی قرار دهیم، می‌توانیم مسافت پیموده شده را در لحظه انفجار نیز محاسبه کنیم. اما قبل از آن بایستی سرعت اولیه را در راستای x بدست آوریم. از آنجایی که جسم در راستای افقی شتابی ندارد، در نتیجه سرعت افقی جسم در تمامی لحظات برابر با همان سرعت اولیه است. برای محاسبه مسافت پیموده شده در لحظه انفجار می‌توان به ترتیب زیر عمل کرد.

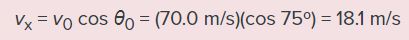
در بعضی از سوالات مربوط به حرکت پرتابی، ممکن است ارتفاع اولیه الزاما در x و y برابر با صفر قرار نداشته باشند. در چنین سوالاتی با توجه به خواسته‌های مسئله بایستی دستگاه مختصات x-y به شکلی در نظر گرفته شود که کم‌ترین محاسبات ممکن نیاز باشد. برای درک بهتر مثالی در ادامه ذکر شده که جسم پرتاب شده، از ارتفاع خاصی شروع به حرکت می‌کند.

مثال ۲

کوه «Kilauea» در هاوایی یکی از فعال‌ترین آتش‌‌فشان‌های دنیا است. در این کوه‌ها معمولا همواره مواد مذاب و سنگ به بیرون پرتاب می‌شود. مطابق شکل زیر فرض کنید که تکه سنگی بزرگ با سرعت ۲۵ متر بر ثانیه و در زاویه ۳۵ درجه نسبت به افق از دهانه کوه به بیرون پرتاب شود.

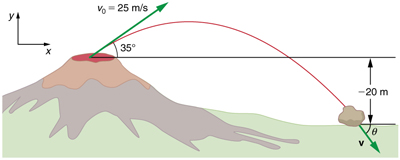
با فرض این‌که ارتفاع کوه برابر با ۲۰ متر باشد، موارد زیر را محاسبه کنید.

1. مدت زمانی که طول می‌کشد تا سنگ به دامنه کوه برسد.
2. زاویه و سرعتِ برخورد سنگ به زمین چقدر است؟

فیلم آموزش فیزیک پایه ۱ – مرور و حل تست در فرادرس

کلیک کنید

همان‌طور که در بالا نیز بیان شد، در ابتدا بایستی دستگاه مختصات مناسب را انتخاب کنید. در این مسئله مبدا دستگاه x-y را روی قله قرار می‌دهیم.

در قسمت اول مسئله، مجهول ما زمان است، بنابراین می‌توان با استفاده از معادله حرکت در راستای y، زمان خواسته شده را به شکل زیر محاسبه کرد. البته توجه داشته باشید که با توجه به دستگاه مختصات انتخاب شده،‌ نقطه y₂ برابر با ۲۰- متر در نظر گرفته می‌شود.

به منظور استفاده از معادله بالا،‌ در ابتدا بایستی سرعت اولیه در راستای y را بدست آوریم. این سرعت برابر است با:

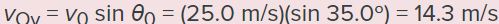
با جایگذاری ۱۴.۳ در معادله شماره ۱، داریم:

این معادله یک رابطه درجه ۲ با مجهول t است که با حل آن، زمان t برابر با ۳.۹۶ بدست می‌آید.

برای محاسبه زاویه برخورد بایستی مولفه‌های سرعت در راستای x و y را داشته باشیم. از این رو در ابتدا دو سرعت مذکور را می‌یابیم. هم‌چنین به‌منظور محاسبه سرعت افقی در لحظه برخورد، سرعت اولیه در راستای x را بایستی محاسبه کنیم. نهایتا مولفه‌های سرعت افقی و قائم، در لحظه برخورد را می‌توان به‌ترتیب مراحل زیر محاسبه کرد.

با بدست آمدن دو سرعت x و y در لحظه برخورد، زاویه برخورد را به شکل بدست می‌آوریم.

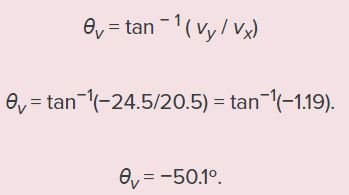
یکی از مهم‌ترین برداشت‌هایی که می‌توان از حرکت پرتابی داشت، این است که در آن‌ها حرکت افقی و عمودی جسم به هم وابسته نیستند و می‌توان آن‌ها را به طور جدا تحلیل کرد. گالیله اولین شخصی بود که این مفهوم را ارائه کرد. در حرکت پرتابی می‌توان عددی تحت عنوان «برد» (Range) تعریف کرد که با R نشان داده می‌شود.

برد عبارت است از بیشترین ‌مسافت افقی که یک پرتابه طی می‌کند. اگر جسمی با سرعت اولیه V₀ و تحت زاویه θ_۰ نسبت به افق پرتاب شود، بیشترین مسافت افقی پیموده شده توسط آن را می‌توان با استفاده از رابطه زیر محاسبه کرد.

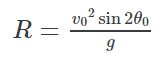
مثال ۳

فیزیکدانی در مسابقات پرتاب دیسک شرکت می‌کند! او از قبل محاسبه کرده برای این‌ که دیسک پرتابیش بیشترین مسافت ممکن را طی کند، بایستی با چه زاویه‌ای این پرتاب را انجام دهد. به نظر شما او زاویه اولیه پرتاب را چه عددی بدست آورده؟

مطابق با رابطه ارائه شده در بالا بیشترین برد ممکن برای یک پرتابه زمانی اتفاق می‌افتد که عبارت (sin (2θ₀ به بیشترین مقدار خود برسد. همان‌طور که از ریاضیات می‌دانید بیشترین مقدار این عبارت برابر با ۱ است و زمانی این اتفاق می‌افتد که 2θ0 برابر با ۹۰ درجه باشد. بنابراین می‌توان گفت:

$$sin2 \theta_0=1\rightarrow 2θ_0=90^0 \rightarrow θ_0=45^0$$

در صورت علاقه‌مندی به مباحث مرتبط در زمینه فیزیک پایه می‌توانید به آموزش‌های زیر مراجعه کنید:

• مجموعه آموزشی دروس دبیرستان
• مجموعه آموزش‌های ریاضی و فیزیک
• قانون دوم نیوتن -- به زبان ساده
• تُندی و سرعت — به زبان ساده
• ضرب داخلی بردارها — به زبان ساده
• معادله درجه دو -- به زبان ساده