مومنتوم خطی (Linear Momentum) در سیالات — از صفر تا صد

در مطالب قبلی وبلاگ فرادرس به بررسی قانون بقای جرم و معادله پیوستگی پرداخته شد. برای محاسبه سرعت میدان جریان سیال، ضروری است که بر معادلات «مومنتوم» (momentum) خطی و زاویهای و قوانین حاکم برآنها تسلط کافی داشته باشیم. مومنتوم را تکانه نیز مینامند و در مطلب تکانه وبلاگ فرادرس به بررسی تکانه جسم صلب پرداخته شد ولی محاسبه مومنتوم یا تکانه در مکانیک سیالات پیچیدگیهای خاص خود را دارد. معادلات مومنتوم خطی و مومنتوم زاویهای به صورت کلی با توجه به قانون دوم نیوتن به دست میآیند و کاربرد زیادی در به دست آوردن معادلات ناویر استوکس و محاسبات موجود در دینامیک سیالات محاسباتی دارند. در این مطلب، مفهوم مومنتوم خطی و شیوه بهدست آوردن روابط حاکم بر آن مورد بحث قرار میگیرند. در ادامه برای آشنایی با کاربرد معادلات مومنتوم خطی در مسائل مکانیک سیالات، مثالی نیز آورده شده است.
معادله مومنتوم خطی
قانون دوم نیوتن بیان میکند که نرخ زمانی تغییرات «مومنتوم خطی» (Linear Momentum) یک سیستم، برابر با مجموع نیروهای خارجی است که به آن سیستم وارد میشوند. مومنتوم خطی یا تکانه خطی به صورت کلی برابر با حاصل ضرب جرم یک جسم در سرعت آن تعریف میشود. این مفهوم در مکانیک سیالات به صورت یک رابطه انتگرالی نوشته میشود بنابراین در ابتدا نیاز به تعیین المان انتگرال روی یک جز کوچک سیستم داریم.
مومنتوم این جز کوچک سیستم که جرمی برابر با دارد، به صورت تعریف میشود و مومنتوم کل این سیستم را میتوان با انتگرالگیری روی تمام اجزای سیستم به فرم محاسبه کرد. بنابراین با توجه به توضیحات ارائه شده، فرم انتگرالی قانون دوم نیوتن برای یک سیستم به صورت زیر نوشته میشود.
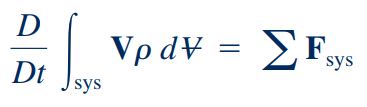
نکتهای که باید به آن توجه کرد این است که رابطه فوق برای مرجع لخت معتبر است. سیستم مختصاتی که ساکن باشد یک نوع مرجع لخت است. سیستم مختصاتی که روی خط راست و با سرعت ثابت و بدون شتاب حرکت میکند نیز یک سیستم لخت در نظر گرفته میشود. همانطور که اشاره شد، تعریف صحیح حجم کنترل یکی از مباحث مهم در مسائل مکانیک سیالات است. در این بخش نیز ما به دنبال یافتن تعریف مناسبی برای رابطه فوق در حالت حجم کنترلی هستیم. بنابراین حجم کنترلی که به سیستم متصل است، مطابق شکل زیر در نظر گرفته میشود. در این مجموعه نیروهای وارد بر حجم کنترل و سیستم یکسان هستند و به فرم زیر نمایش داده میشوند.
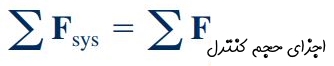
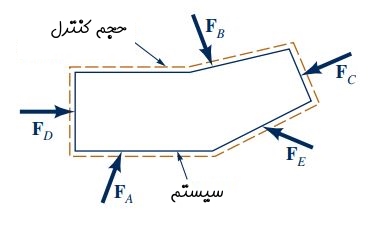
برای یک حجم کنترل که مشابه شکل بالا منطبق بر سیستم و فاقد سرعت و تغییر شکل است، رابطه انتقال رینولدز را میتوانیم باز نویسی کنیم (برای مطالعه جزئیات رابطه انتقال رینولدز به مطلب «پیوستگی و بقای جرم در سیالات -- از صفر تا صد» مراجعه کنید). در ادامه، پارامتر b در معادله انتقال رینولدز را برابر با سرعت در نظر میگیریم، در این صورت برابر با مومنتوم سیستم میشود و در نهایت فرم نهایی معادله انتقال رینولدز به شکل زیر در میآید:

ترم سمت چپ معادله بالا نشان دهنده نرخ تغییرات مومنتوم خطی سیستم است که با مشتق مادی نشان داده میشود. این ترم در معادله بالا به صورت مجموع دو عبارت وابسته به حجم کنترل نوشته میشود. عبارت اول، نرخ تغییرات مومنتوم خطی محتویات حجم کنترل است و عبارت دوم نرخ جریان مومنتوم از سطوح حجم کنترل را نشان میدهد. به عبارت دیگر ذراتی که به داخل و یا خارج از حجم کنترل در حال حرکت هستند، با خود مومنتوم خطی حمل میکنند. در نهایت با جایگذاری روابط ۱ و ۲ در رابطه ۳، فرم نهایی معادله مومنتوم خطی برای یک حجم کنترل ساکن و بدون تغییر شکل مطابق با رابطه زیر به دست میآید.
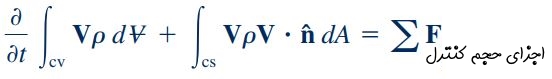
در این رابطه، عبارت سمت راست معادله نشان دهنده تمام «نیروهای سطحی» (Surface Forces) و «نیروهای حجمی» (Body Forces) است که بر حجم کنترل وارد میشوند. در اکثر مسائل مکانیک سیالات تنها نیروی حجمی که برای رابطه فوق در نظر گرفته میشود، نیروی گرانش است.
در صورتی که حجم کنترل انتخاب شده، با سرعت ثابت حرکت کند و تغییر شکلی در آن رخ ندهد باز هم رابطه مومنتوم خطی به دلیل شتاب صفر و لخت بودن سیستم، برای این سیستم و حجم کنترل قابل بیان است. در این حالت نیاز به بازنویسی معادله انتقال رینولدز داریم. همانند قسمت قبل، پارامتر در رابطه انتقال رینولدز را برابر با مومنتوم سیستم در نظر میگیریم. بنابراین فرم نهایی معادله انتقال رینولدز برای حجم کنترلی که با سرعت ثابت حرکت میکند و تغییر شکلی در آن رخ نمیدهد، به فرم زیر در میآید.
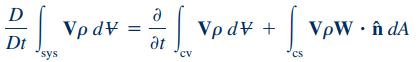
در رابطه بالا، W سرعت نسبی سیال نسبت به حجم کنترل را نشان میدهد و برای به دست آوردن معادله مومنتوم خطی نیاز است که روابط ۱ و ۲ در رابطه فوق جایگذاری شوند. در نهایت معادله مومنتوم خطی برای حجم کنترلی که با سرعت ثابت حرکت میکند و تغییر شکلی در آن رخ نمیدهد به شکل زیر خواهد بود.
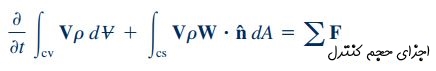
مهمترین پارامتر در معادله بالا، سرعت سیال نسبت به حجم کنترل متحرک است که برای محاسبه آن میتوان از رابطه زیر استفاده کرد. در این رابطه، ارتباط بین سرعتهای مختلف در حجم کنترل، نشان داده شده است.
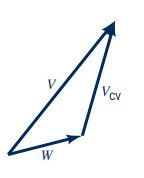
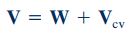
W سرعت نسبی سیال را نشان میدهد و برابر با سرعتی است که توسط ناظر متحرک با حجم کنترل، دیده میشود. سرعت مطلق حجم کنترل را نشان میدهد که برابر با سرعت حجم کنترل نسبت به ناظر ساکن است. V نیز سرعت مطلق سیال است که نسبت به ناظر ساکن اندازهگیری میشود. بنابراین با جایگذاری رابطه سرعت نسبی (رابطه 7) در فرم کلی انتگرالی معادله مومنتوم (رابطه 6)، معادله نهایی مومنتوم خطی به شکل زیر بازنویسی میشود.
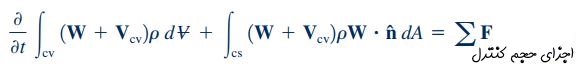
در صورتی که جریان در این حجم کنترل، به صورت پایا فرض شود، ترم اول در سمت چپ معادله فوق را میتوان به شکل زیر نمایش داد.
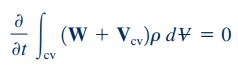
همچنین ترم دوم سمت چپ رابطه ۸ برای حجم کنترلی که با سرعت ثابت حرکت میکند و تغییر شکلی در آن رخ نمیدهد را میتوان به فرم زیر نمایش داد.

در این حجم کنترل، رابطه پیوستگی به شکل زیر قابل نمایش است:
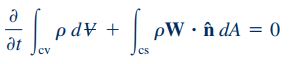
زمانی که جریان به صورت پایا فرض شده باشد، ترم اول در رابطه پیوستگی (رابطه ۱۱) برابر با صفر خواهد بود و فرم نهایی معادله پیوستگی برای حالت پایا به شکل زیر در میآید.
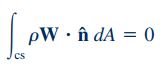
بنابراین با ترکیب معادلات 8، 9، 10 و 12، برای حجم کنترلی که با سرعت ثابت حرکت میکند، قابلیت تغییر شکل ندارد و جریان در آن به صورت پایا فرض شده است، معادله مومنتوم خطی به شکل زیر بانویسی میشود:
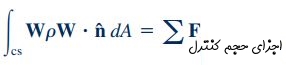
در ادامه و در قالب مثالی مفهوم مومنتوم خطی و شیوه استفاده از روابط حاکم بر آن را مورد بررسی قرار میدهیم.
مثال
جریان آب، مطابق شکل زیر از درون یک نازل با دبی 0.6liters/s عبور میکند. قطر ورودی و خروجی این نازل به ترتیب برابر با 16 و ۵ میلیمتر هستند. جرم نازل را 0.1 کیلوگرم و فشار در مقطع ۱ آن را برابر با 464 کیلوپاسکال در نظر بگیرید.
نیرویی لازم برای ثابت نگه داشتن این نازل را با استفاده از معادله مومنتوم خطی محاسبه کنید.
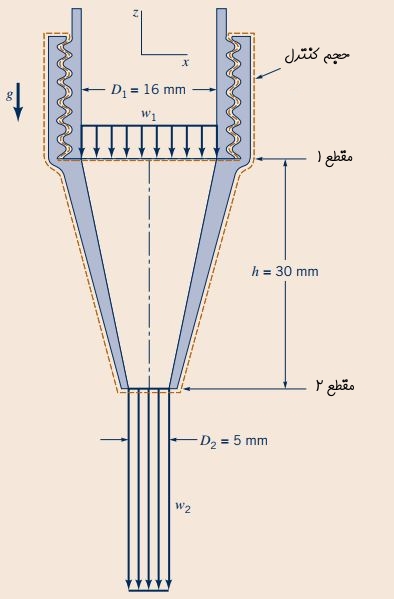
قدم اول در حل اکثر مسائل مکانیک سیالات انتخاب حجم کنترل مناسب است. در این مثال، این حجم کنترل طوری در نظر گرفته میشود که تمام نازل و آبی که هر لحظه در آن جریان دارد را در بر گیرد. این حجم کنترل در هر دو شکل بالا و پایین با خطچین نشان داده شده است. قدم بعدی برای نوشتن معادله مومنتوم خطی، مشخص کردن نیروهای وارد بر حجم کنترل است. در شکل زیر نیروهای عمودی وارد بر اجزای این حجم کنترل به تصویر کشیده شدهاند.
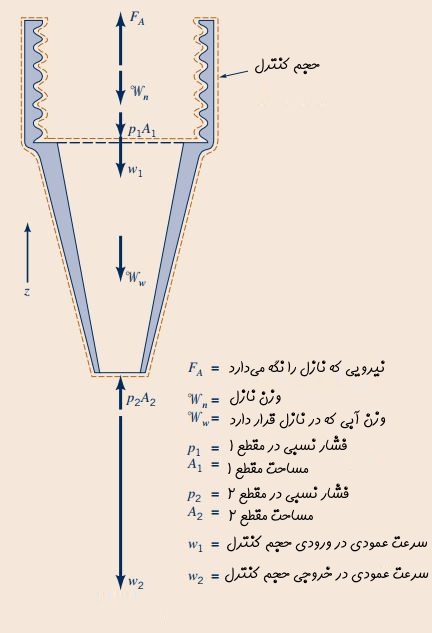
توجه شود که نیروی فشار اتمسفری به طور یکسان در ورودی و خروجی وارد میشود بنابراین این دو نیرو اثر یکدیگر را خنثی میکنند؛ به همین دلیل، در شکل بالا این دو نیرو نشان داده نشدهاند. اما باید توجه کرد که نیروی حاصل از فشار نسبی در قسمت پایین و خروجی نازل با هیچ نیرویی خنثی نمیشود و این نیرو در شکل بالا به تصویر کشیده شده است.
پس از مشخص کردن حجم کنترل و نیروهای وارد بر آن، نوبت نوشتن معادله مومنتوم خطی است. این معادله در حالت کلی به صورت زیر نشان داده میشود.
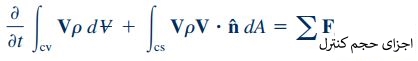
در این مثال، اجزایی از معادله بالا که در راستای z هستند برای ما اهمیت دارند. بنابراین معادله مومنتوم خطی را در راستای z به شکل زیر بازنویسی میکنیم.
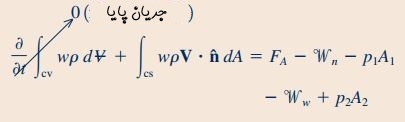
ترم اول این رابطه با توجه به اینکه جریان به صورت پایا فرض شده است، برابر با صفر در نظر گرفته میشود. توجه شود که در معادله مومنتوم خطی، جهت مثبت به سمت بالا فرض شده است. نکته دیگری که باید به آن اشاره کرد این است که در رابطه بالا ضرب داخلی برای جریان به سمت خارج حجم کنترل مثبت و برای جریان به سمت داخل حجم کنترل منفی است. این مورد در رابطه زیر مشاهده میشود.
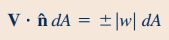
ترم دوم سمت چپ معادله مومنتوم خطی (رابطه ۱۵)، شامل انتگرالی روی سطح کنترل است و برای محاسبه آن باید توزیع مناسبی از سرعت و چگالی سیال در ورودی و خروجی حجم کنترل، تعیین شود.
در این مثال، فرض میشود که سرعت در ورودی و خروجی، توزیع یکنواختی دارند. در ادامه و با توجه به فرض غیر قابل تراکم بودن جریان، چگالی سیال ثابت و برابر با در نظر گرفته میشود. در نهایت معادله مومنتوم خطی (رابطه ۱۵) به شکل زیر در میآید.
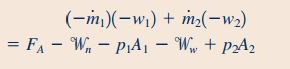
در این معادله جریان جرمی را نشان میدهد و با رابطه زیر تعیین میشود.
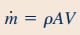
با سادهسازی رابطه 17 مقدار نیروی دیواره که خواسته مسئله است به شکل زیر محاسبه میشود.
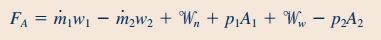
با نوشتن رابطه بقای جرم برای حجم کنترل در نظر گرفته شده، مشاهده میشود که جریان جرمی در ورودی و خروجی این حجم کنترل برابر هستند. بنابراین رابطه بالا به شکل زیر ساده میشود.

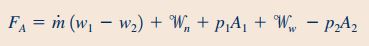
برای محاسبه نیروی دیواره که در رابطه ۱۹ نشان داده شده است نیاز به محاسبه مقادیر سرعت و وزن سیال داریم. سرعت سیال در مقطع ۱ را به کمک رابطه جریان جرمی و به شکل زیر محاسبه میکنیم.
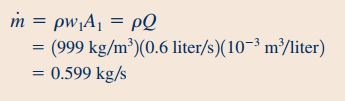
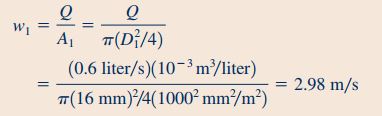
روندی که در معادله بالا برای محاسبه سرعت در مقطع ۱ استفاده شد را برای به دست آوردن سرعت در مقطع ۲ نیز استفاده میکنیم. بنابراین داریم:
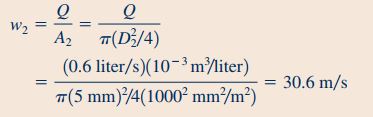
همانطور که اشاره شد یکی دیگر از پارامترهای مورد نیاز برای محاسبه نیروی دیواره در رابطه ۱۹، وزن نازل است که برای به دست آوردن آن از رابطه زیر استفاده میکنیم.
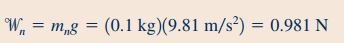
در ادامه و برای محاسبه وزن آب موجود در حجم کنترل ابتدا نیاز به محاسبه حجم نازل داریم و برای به دست آوردن آن به صورت زیر عمل میکنیم.
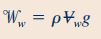
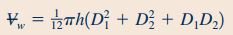
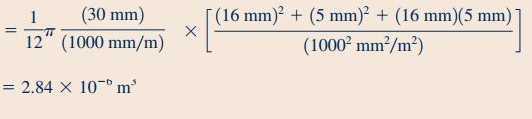
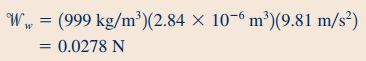
با جایگذاری مقادیر محاسبه شده در رابطه ۱۹، مقدار نیرویی که برای ثابت نگه داشتن این نازل مورد نیاز است، به شکل زیر محاسبه میشود.
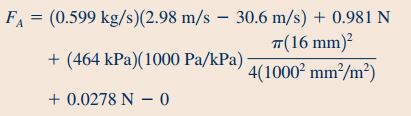
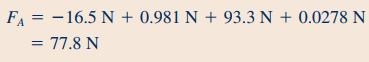
در این مطلب مفهوم مومنتوم خطی و روابط حاکم بر آن به صورت کامل مورد بررسی قرار گرفت و نحوه استفاده از این روابط در قالب یک مثال نشان داده شد. در مطالب بعدی وبلاگ فرادرس به بررسی مفهوم مومنتوم زاویهای پرداخته شده است.
در صورتی که به مباحث ارائه شده، علاقهمند هستید و قصد یادگیری در زمینههای مطرح شده در مکانیک سیالات را دارید، آموزشهای زیر به شما پیشنهاد میشود:
- مجموعه آموزشهای دروس مهندسی مکانیک
- مجموعه آموزشهای نرمافزارهای مهندسی مکانیک
- آموزش مکانیک سیالات
- مجموعه آموزشهای دروس مهندسی شیمی
- پیوستگی و بقای جرم در سیالات — از صفر تا صد
- سینماتیک سیالات — مقدمهای بر مکانیک
- دینامیک سیالات محاسباتی (CFD) — از صفر تا صد
- مومنتوم زاویهای (Moment of Momentum) در سیالات -- آموزش سریع و ساده
^^












این توضیحات برای افرادی است که نابینا هستند؟
این که فقط متن رو روخوانی میکنه.