پاسخ پله — از صفر تا صد

۵۵۶۳ بازدید

آخرین به‌روزرسانی: ۲۴ اردیبهشت ۱۴۰۲

زمان مطالعه: ۲۹ دقیقه

یکی از مهم‌ترین ورودی‌های تست سیستم، تابع پله واحد (Unit Step Function) است. پاسخ یک سیستم با شرایط اولیه صفر یا به عبارت دیگر، پاسخ حالت صفر (Zero State Response) یک سیستم به ورودی پله واحد را پاسخ پله واحد می‌گویند. البته اگر سیستم مورد بررسی دارای شرایط اولیه غیر صفر باشد، نیاز است که برای به دست آوردن پاسخ کامل، پاسخ ورودی صفر را نیز محاسبه کرد. در این مطلب می‌خواهیم به بررسی پاسخ پله (Unit Step Response) برای سیستم درجه یک، سیستم درجه دو و سیستم‌های درجه بالاتر بپردازیم.

فهرست مطالب این نوشته

حل عمومی

پاسخ پله سیستم مرتبه اول

پاسخ پله سیستم مرتبه دو

پاسخ پله سیستم مرتبه دو بالا گذر (Highpass)

پاسخ پله سیستم مرتبه دوم میان گذر (Bandpass)

پاسخ پله در متلب

حل عمومی

در تصویر زیر می‌توان تصویر تابع پله واحد را مشاهده کرد.

می‌توان ورودی پله یک سیستم را به سادگی با استفاده از تابع انتقال (Transfer Function) آن به دست آورد.

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

اگر در یک سیستم ورودی برابر با $$ x(t) $$، خروجی برابر با $$ y(t) $$ و تابع انتقال $$ H(S) $$ باشد، آن‌گاه می‌توان نوشت:

$$ H(S) = \frac {Y(S)} {X(S)} $$

در این سیستم، خروجی با شرایط اولیه صفر یا به عبارت دیگر خروجی حالت صفر، به سادگی با فرمول زیر محاسبه می‌شود:

$$ Y(S) = X(S) H(S) $$

بنابراین، پاسخ پله واحد $$ Y _ \gamma (S) $$ به صورت زیر محاسبه می‌شود:

$$ Y _ \gamma (S) = \frac {1} {S} H(S) $$

حال با اعمال قضیه مقدار اولیه و مقدار نهایی، می‌توانیم دو مشخصه بسیار مهم از پاسخ پله واحد، یعنی مقادیر اولیه و نهایی آن را تعیین کنیم. بر همین اساس، مقدار اولیه تابع برابر است با:

$$ \lim_{t \rightarrow 0 ^+} f(t) = \lim_{S \rightarrow \infty} S F(S) $$

مقدار نهایی نیز به صورت زیر به دست می‌آید:

$$ \lim_{t \rightarrow \infty} f(t) = \lim_{S \rightarrow 0} S F(S) $$

بنابراین داریم:

$$ \lim_{t \rightarrow 0 ^+} Y _ \gamma (t) = \lim_{S \rightarrow \infty} S Y _ \gamma (S) = \lim_{S \rightarrow \infty} S \frac {1} {S} H(S) = \lim_{S \rightarrow \infty} H(S) $$

$$ \lim_{t \rightarrow \infty} Y _ \gamma (t) = \lim_{S \rightarrow 0} S Y _ \gamma (S) = \lim_{S \rightarrow 0} S \frac {1} {S} H(S) = \lim_{S \rightarrow 0} H(S) $$

معمولا این معادله‌ها را ساده می‌کنیم و می‌نویسیم:

$$ Y _ \gamma (0^+) = H ( \infty ) $$

$$ Y _ \gamma (\infty) = H ( 0 ) $$

پاسخ پله سیستم مرتبه اول

ابتدا یک سیستم عمومی را در نظر می‌گیریم و پاسخ پله را برای آن محاسبه می‌کنیم. در ادامه مثال‌های بیشتری را از سیستم‌های درجه یک حل می‌کنیم.

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

یک تابع انتقال مرتبه اول عمومی را در نظر بگیرید که توسط رابطه زیر توصیف می‌شود:

$$ H(S) = \frac {b.S + c} {S+ a} $$

در این سیستم، $$ a $$ و $$ b $$ و $$ c $$ اعداد حقیقی هستند و یکی از مقادیر $$ b $$ یا $$ c $$ ممکن است برابر با صفر باشند، اما هر دو با هم صفر نمی‌شوند. برای به دست آوردن پاسخ پله واحد، $$ H(S) $$ را در $$ \frac {1} {S} $$ ضرب می‌کنیم:

$$ Y_ \gamma (S) = \frac {1} {S} H(S) = \frac {1} {S} \frac {b.S + c} {S+ a} $$

با استفاده از تبدیل لاپلاس معکوس و بسط کسرهای جزئی می‌توان نوشت:

$$ Y_ \gamma (S) = \frac {1} {S} H(S) = \frac {1} {S} \frac {b.S + c} {S+ a} \\
Y_ \gamma (S) = \frac{A} {S } + \frac{B} {S+ a} \\
= \frac{c} {a }\frac{1} {S } + \frac{ba - c} { a} \frac{1} {S+ a}\\
= \frac{c} {a }\frac{1} {S } + (b - \frac{ c} { a}) \frac{1} {S+ a} $$

بنابراین:

$$ Y_ \gamma ( t) = \frac{ c} { a} + (b - \frac{ c} { a}) e^ {-at}\; ,\;\;\;t>0 $$

حال می‌توان مشخصه‌های بسیاری را از این معادله به دست آورد:

$$ Y_ \gamma (0^ +) = H(\infty ) = b $$

$$ Y_ \gamma ( \infty ) = H( 0 ) = \frac{ c} { a} $$

$$ \tau = \frac{1} { a} $$

بنابراین می‌توان فرم عمومی پاسخ پله واحد سیستم را به صورت زیر نوشت:

$$\large Y_ \gamma (t) = Y_ \gamma (\infty) + (Y_ \gamma (0 ^ +) - Y_ \gamma (\infty)) e^ {- \frac {t} {\tau}} $$

$$ \large = H (0 ) + ( H ( \infty) - H( 0) ) e ^ {\frac {- t} {\tau} } $$

معادلات فوق از اهمیت بالایی برخوردارند. بر اساس این معادلات می‌توان نتیجه گرفت که اگر بتوان مقادیر اولیه یک سیستم مرتبه اول را در $$ t = 0 ^ + $$ تعیین کرد، آن‌گاه می‌توان مقدار نهایی و نیز ثابت زمانی سیستم را به دست آورد و برای این کار به حل هیچ معادله‌ای نیاز نداریم. به طریق مشابه، اگر بتوانیم مقادیر اولیه سیستم را از راه تجربی به دست آوریم و سپس مقدار نهایی و ثابت زمانی را تعیین کنیم، آن‌گاه می‌توانیم تابع انتقال کلی سیستم را محاسبه کرد.

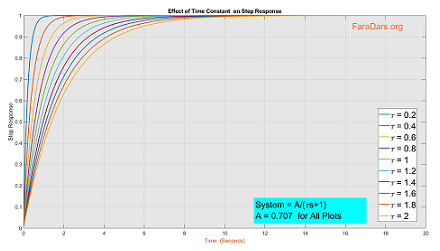
ثابت زمانی سیستم مرتبه اول

محاسبه ثابت زمانی سیستم مرتبه اول معمولا ساده است. ثابت زمانی برخی از سیستم‌های متداول در جدول زیر آورده شده‌اند.

ثابت زمانی	نوع سیستم
$$ m/b $$	سیستم انتقالی جرم و دمپر
$$b/k $$	سیستم انتقالی دمپر و فنر
$$ J/B_r $$	سیستم دورانی چرخ و دمپر
$$ B_r/K_r $$	سیستم دورانی چرخ و فنر
$$ R.C $$	مدار خازن و مقاومت
$$ L/R $$	مدار خازن و سلف
$$ R.C $$	حرارتی

مثال ۱

اگر نیروی ورودی سیستم زیر برابر با پله واحد باشد، آن‌گاه $$ v(t) $$ را محاسبه کنید.

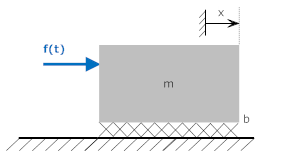
دیاگرام نیروها در این سیستم به صورت زیر نشان داده شده است.

حل اول

معادله دیفرانسیل توصیف کننده سیستم برابر است با:

$$ m \dot{v} + b v = f(t) $$

بنابراین تابع انتقال را با اعمال تبدیل لاپلاس (با شرایط اولیه صفر) و حل کردن $$ V(S) / F(S) $$ به دست می‌آوریم:

$$ m S V(S) + b V (S) = F(S) $$

$$ \frac {V(S)} {F(S)} = H(S) = \frac {1} {ms + b} = \frac {1/m} {s + b/m} $$

برای به دست آوردن پاسخ پله واحد، تابع انتقال را در تبدیل لاپلاس پله واحد یعنی $$ \frac {1} {S} $$ ضرب می‌کنیم و سپس معادله را با نگاه کردن به جدول تبدیل لاپلاس و یافتن معکوس حل می‌کنیم:

$$ V(S) = F(S) H(S) = \frac {1} {S} \frac {1/m} {s + b/m} $$

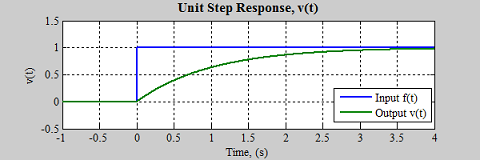
$$ v(t) = \frac {1} {b} (1 - e^ { - (\frac {b } {m}) t }) $$

با فرض کردن $$ m=b=1 $$، جواب به صورت زیر به دست می‌آید.

حل دوم (بدون نیاز به لاپلاس معکوس)

با استفاده از تابع انتقال می‌توان اطلاعات زیر را به دست آورد:

$$ V (0^ +) = H(\infty ) = 0 $$

$$ V ( \infty ) = H( 0 ) = \frac{ 1} { b} $$

$$ \tau = \frac{m} { b} $$

حال با استفاده از فرم عمومی پاسخ پله واحد سیستم‌های مرتبه اول، به رابطه زیر دست می‌یابیم:

$$ v (t) = v (\infty) + (v (0 ^ +) - v (\infty)) e^ {- \frac {t} {\tau}} $$

$$ = H (0 ) + ( H ( \infty) - H( 0) ) e ^ {\frac {- t} {\tau} } $$

$$ = \frac {1} {b} + (0 - \frac {1} {b}) e^ {- \frac {b} {m} t} $$

$$ = \frac {1} {b} (1 - e^ {- \frac {b} {m} t} ) $$

همچنین می‌توان از روش زیر استفاده کرد.

سیستم از حالت سکون شروع به حرکت می‌کند و سرعت جرم در سیستم فوق نمی‌تواند با یک ورودی محدود، به صورت آنی تغییر کند، بنابراین $$ v (0 ^ + ) = 0 $$. سرعت نهایی از جرم مستقل است؛ زیرا هیچ نیروی شتابی در سرعت ثابت وجود ندارد.

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

بنابراین داریم:

$$ f(\infty)=bv(\infty)\;\; or \;\;v(\infty)=\frac {f(\infty)}{b}=\frac {1} {b} $$

ثابت زمانی یک سیستم جرم و دمپر برابر با $$\frac {m} {b} $$ است. بنابراین:

$$ v(t) = \frac {1} {b} (1 - e^ {- \frac {b} {m} t} ) $$

مثال ۲

اگر نیروی ورودی سیستم زیر، یک پله با دامنه $$ X_0 $$ باشد، آن‌گاه خروجی $$ y(t) $$ را به دست آورید.

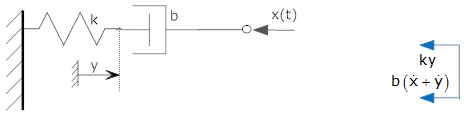
حل اول

توجه کنید که ورودی سیستم، تابع پله واحد نیست، بلکه دارای دامنه $$ X_0 $$ است. بنابراین تمام خروجی سیستم نیز باید دارای مقیاس $$ X_0 $$ باشد. معادله دیفرانسیل توصیف کننده سیستم به صورت زیر نوشته می‌شود:

$$ b \dot{y} + ky = -b \dot{x} (t) $$

بنابراین تابع انتقال را با اعمال تبدیل لاپلاس به طرفین معادله محاسبه می‌کنیم و سپس نسبت $$ \frac{ Y(S) } { X(S) } $$ را به دست می‌آوریم:

$$ \frac{ Y(S) } { X(S) } = H(S) = - \frac {S} {S + \frac {k} {b}} $$

برای به دست آوردن پاسخ پله واحد، تابع انتقال را در تابع پله با دامنه $$ X_0 $$ یعنی $$ \frac {X_0} {S} $$ ضرب می‌کنیم. سپس معادله را با جست و جو در جدول تبدیل لاپلاس و محاسبه لاپلاس معکوس به دست می‌آوریم:

$$ \frac{ Y(S) } { X(S) } = H(S) = - \frac {X_0} {S} \frac {S} {S + \frac {k} {b}} $$

$$ = - \frac { X_0 } {S + \frac {k} {b}} $$

$$ = y(t) = - X_0 e^ {- \frac {k} {b} t} $$

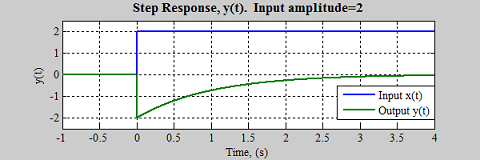
به ازای مقادیر $$ k = b = 1 $$ و $$ X_0 = 2 $$، جواب زیر برای این سیستم به دست می‌آید.

حل دوم (بدون نیاز به تبدیل لاپلاس معکوس)

با استفاده از تابع انتقال، می‌توان ویژگی‌های زیر را به دست آورد:

$$ y (0^ +) = X_0 H(\infty ) = - X_0 $$

$$ y ( \infty ) = X_0 H( 0 ) = 0 $$

$$ \tau = \frac{b} { k} $$

با استفاده از فرم عمومی پاسخ پله واحد در یک سیستم مرتبه اول، داریم:

$$ y (t) = y (\infty) + (y (0 ^ +) - y (\infty)) e^ {- \frac {t} {\tau}} $$

$$ = 0 + (- X_0 - 0) e ^ {-(\frac {k} {b} )t} $$

$$ = - X_0 e ^ {-(\frac {k} {b} )t} $$

همچنین می‌توان از روش زیر استفاده کرد و به پاسخ مشابهی دست یافت.

طول دمپر با اعمال نیروی محدود به صورت آنی تغییر نمی‌کند، بنابراین $$ X(0^ + ) = - X_0 $$ است. موقعیت نهایی مستقل از دمپر است؛ زیرا در سرعت صفر، هیچ نیروی اصطکاکی وجود ندارد و $$ X(\infty ) = 0 $$ است. ثابت زمانی در سیستم دمپر و فنر برابر با $$ \frac {b} {k} $$ است. بنابراین:

$$ y(t) = - X_0 e ^ {-(\frac {k} {b} )t} $$

مثال ۳

در مدار زیر، اگر ولتاژ ورودی $$ e_{in} (t) $$ برابر با پله واحد باشد، آن‌گاه مقدار $$ e_{out} (t)$$ را بیابید.

حل اول

ابتدا باید تابع انتقال مدار را به دست آوریم. می‌دانیم که مدار مربوط به یک مقسم ولتاژ با دو مقاومت است. بنابراین می‌توان شماتیک مدار را به صورت زیر رسم کرد.

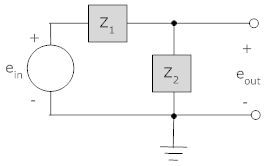
تابع انتقال برابر است با:

$$ \frac {E_{out} (S)} { E_{in} (S)} = H(S) = \frac {Z_2} {Z_2 + Z_1} $$

در این تابع انتقال، $$ Z_1 $$ برابر با $$ R_1 $$ و $$ Z_2 $$ برابر با ترکیب سری $$ R_2 $$ و خازن $$ C $$ است. بنابراین داریم:

$$ Z_{1} =R_{1} $$

$$ Z_{2} =Z_{R 2}+Z_{C}=R_{2}+\frac{1}{S C} $$

$$ H(S) =\frac{E_{o u t}(S)}{E_{i n}(S)}=\frac{Z_{2}}{Z_{1}+Z_{2}}=\frac{R_{2}+\frac{1}{S C}}{R_{1}+R_{2}+\frac{1}{S C}} $$

$$ =\frac{C R_{2}}{C\left(R_{1}+R_{2}\right)} \frac{S+\frac{1}{C\left(R_{1}+R_{2}\right)}}{C\left(R_{1}+R_{2}\right)} $$

$$ =\frac{R_{2}}{\left(R_{1}+R_{2}\right)} \frac{1}{S+\frac{1}{C\left(R_{1}+R_{2}\right)}} $$

برای به دست آوردن پاسخ پله واحد سیستم، تابع انتقال سیستم را در تبدیل لاپلاس تابع پله واحد $$ \frac {1} {S} $$ ضرب می‌کنیم و سپس با استفاده از تبدیل لاپلاس معکوس، پاسخ را به دست می‌آوریم:

$$ \mathrm{E}_{\mathrm{ous}}(\mathrm{s}) =\frac{1}{\mathrm{s}} \mathrm{H}(\mathrm{s})=\frac{1}{\mathrm{s}} \frac{\mathrm{R}_{2}}{\left(\mathrm{R}_{1}+\mathrm{R}_{2}\right)} \frac{\mathrm{s}+\frac{1}{\mathrm{CR}_{2}}}{\mathrm{s}+\frac{1}{\mathrm{C}\left(\mathrm{R}_{1}+\mathrm{R}_{2}\right)}} $$

$$ =\frac{\mathrm{A}}{\mathrm{s}}+\frac{\mathrm{B}}{\mathrm{s}+\frac{1}{\mathrm{C}\left(\mathrm{R}_{1}+\mathrm{R}_{2}\right)}} $$

$$ =\frac{1}{\mathrm{s}}-\frac{\mathrm{R}_{1}}{\left(\mathrm{R}_{1}+\mathrm{R}_{2}\right)} \frac{1}{\mathrm{s}+\frac{1}{\mathrm{C}\left(\mathrm{R}_{1}+\mathrm{R}_{2}\right)}} $$

$$ \mathrm{e}_{\mathrm{out}}(\mathrm{t}) =1-\frac{\mathrm{R}_{1}}{\left(\mathrm{R}_{1}+\mathrm{R}_{2}\right)} \mathrm{e}^{-t /\left(\mathrm{Q}_{1}+\mathrm{r}_{2}\right)} $$

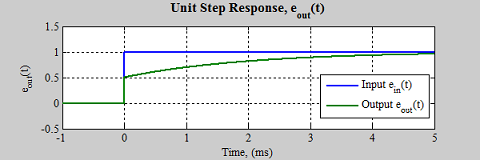
با در نظر گرفتن مقادیر $$ R_1 = R_2 = 1 K \Omega $$ و $$ C = 1 \mu F $$ نتیجه زیر برای سیستم به دست می‌آید.

حل دوم (بدون تبدیل لاپلاس معکوس)

با استفاده از تابع انتقال می‌توان به اطلاعات زیر دست یافت:

$$ e_{out } (0^ + ) = H (\infty) = \frac {R_2 } {(R_2 + R_1)} $$

$$ e_{out } ( \infty ) = H (0) = 1 $$

$$ \tau = C (R_2 + R_1) $$

با استفاده از فرم عمومی پاسخ پله یک سیستم مرتبه اول می‌توان نوشت:

$$ e_{out } (t) = e_{out } ( \infty ) + ( e_{out } (0^+ - e_{out } ( \infty ) ) e^ {- \frac {t} {\tau}} $$

$$ = 1 + ( \frac {R_2 } {(R_2 + R_1)} - 1) e^ {- \frac {t} {C (R_2 + R_1)}} $$

$$ = 1 - \frac {R_1 } {(R_2 + R_1)} e^ {- \frac {t} {C (R_2 + R_1)}} $$

همان طور که دیدیم این راه حل بسیار ساده‌تر است. همچنین، با استفاده از روش زیر به پاسخ مشابهی خواهیم رسید.

در $$ t = 0^+ $$، هیچ ولتاژی در دو سر خازن وجود ندارد. بنابراین مدار یک مقسم ولتاژ ساده است که در آن $$ C . R_{eq} (\infty) = C (R_1 + R_2 ) $$ است. بنابراین نتیجه‌ای که در این حالت به دست می‌آوریم نیز مانند حالت قبل است:

$$ e_{out } (t) = e_{out } ( \infty ) + ( e_{out } (0^+) - e_{out } ( \infty ) ) e^ {- \frac {t} {\tau}} $$

$$ = 1 + ( \frac {R_2 } {(R_2 + R_1)} - 1) e^ {- \frac {t} {C (R_2 + R_1)}} $$

$$ = 1 - \frac {R_1 } {(R_2 + R_1)} e^ {- \frac {t} {C (R_2 + R_1)}} $$

پاسخ پله سیستم مرتبه دو

همان طور که انتظار می‌رود، پاسخ پله یک سیستم مرتبه دو، پیچیده‌تر از پاسخ پله یک سیستم مرتبه اول است. در حالی که پاسخ پله یک سیستم مرتبه اول را می‌توان با استفاده از ثابت زمانی (تعیین از روی قطب‌های سیستم)، مقدار اولیه و مقدار نهایی سیستم به صورت کامل تعریف کرد، پاسخ پله یک سیستم مرتبه دو در حالت کلی با روش‌های پیچیده‌تری محاسبه می‌شود.

فیلم آموزش ریاضی مهندسی – مرور و حل سوالات کنکور دکتری در فرادرس

کلیک کنید

در ابتدا باید توجه کنید که فرم تابع تبدیل یک سیستم مرتبه دو را می‌توان به صورت زیر نوشت:

$$ \frac{{Y(s)}}{{X(s)}} = H(s) = \frac{{a{s^2} + bs + c}}{{{s^2} + ds + e}} $$

در رابطه فوق، $$ a $$ و $$ b $$ و $$ c $$ و $$ d $$ و $$ e $$ همگی اعداد حقیقی هستند و حداقل یکی از اعداد در صورت کسر باید غیر صفر باشد.

پاسخ پله سیستم پایین گذر مرتبه دو

در واقع امکان پذیر نیست که تاثیر هر کدام از این 5 عدد را در تابع انتقال عمومی تفکیک کرد. بنابراین برای سادگی، در این مرحله فرض می‌کنیم $$ a = b = 0 $$ باشند. پس تابع انتقال سیستم را به صورت زیر بازنویسی می‌کنیم:

$$ H(s) = \frac{c}{{{s^2} + ds + e}} = K\frac{{\omega _0^2}}{{{s^2} + 2\zeta {\omega _0}s + \omega _0^2}} $$

سه مقدار در رابطه بالا وجود دارند که عبارتند از:

$$ \eqalign {\omega _0} $$: فرکانس نوسان (Natural (or Resonant) Frequency) یا فرکانس طبیعی بر حسب $$ rad/sec $$.
$$ \zeta = \frac{d}{{2\sqrt e }} $$: نرخ میرایی (Damping Ration) (بدون واحد).
$$ K = \frac{c}{e} $$: بهره (Gain) سیستم که دارای واحد یکسان با $$ y/x $$ است.

انتخاب این ثابت‌ها ممکن است به صورت تصادفی به نظر برسد، اما در ادامه نشان خواهیم داد که با انتخاب مناسب این ثابت‌ها می‌توان محاسبات ریاضی را برای سیستم مرتبه دوم ساده‌تر کرد. هر سه ثابت ذکر شده در بالا دارای تعبیر فیزیکی هستند که منجر به داشتن دید صحیح به سیستم می‌شوند. این سیستم را سیستم مرتبه دوم پایین گذر می‌گویند؛ زیرا پاسخ فرکانسی یک سیستم پایین گذر است.

برای یافتن پاسخ پله واحد سیستم، ابتدا تابع انتقال را در تبدیل لاپلاس تابع پله واحد، یعنی $$ \frac{1}{s} $$ ضرب می‌کنیم. بنابراین داریم:

$$ {Y_\gamma }(s) = \frac{1}{s}H(s) = \frac{1}{s}K\frac{{\omega _0^2}}{{{s^2} + 2\zeta {\omega _0}s + \omega _0^2}} $$

قبل از این‌که $$ y_\gamma (t) $$ را به دست آوریم، ابتدا باید ریشه‌های عبارت موجود در مخرج کسر بالا را به دست آوریم:

$$ s = \frac{{ - 2\zeta {\omega _0} \pm \sqrt {{{\left( {2\zeta {\omega _0}} \right)}^2} - 4\omega _0^2} }}{2} = - \zeta {\omega _0} \pm {\omega _0}\sqrt {{\zeta ^2} - 1} $$

مقدار $$ \zeta $$، منجر به ایجاد ۵ نوع مختلف از سیستم‌ها می‌شود که در جدول زیر آورده شده‌اند:

مشخصه S	ریشه S	مقدار $$ \zeta $$	نام
دو ریشه حقیقی منفی	$$ s = - \zeta {\omega _0} \pm {\omega _0}\sqrt {{\zeta ^2} - 1} $$	$$ \zeta > 1 $$	تندمیرا (Overdamped)
یک ریشه (تکراری) منفی	$$ - {\omega _0} $$	$$ \zeta = 1 $$	میرای بحرانی (Critically Damped)
مختلط مزدوج ($$ j = \sqrt{-1} $$)	$$ s = - \zeta {\omega _0} \pm j{\omega _0}\sqrt {1 - {\zeta ^2}} $$	$$ 0< \zeta < 1 $$	کندمیرا (Underdamped)
موهومی خالص (بدون بخش حقیقی)	$$ s = \pm j{\omega _0} $$	$$ \zeta = 0 $$	نامیرا (Undamped)
موهومی یا حقیقی (همیشه قسمت حقیقی S مثبت)	$$ s = - \zeta {\omega _0} \pm {\omega _0}\sqrt {{\zeta ^2} - 1} $$	$$ \zeta < 0 $$	رشد نمایی (Exponential Growth)

سه گروه اول از سیستم‌ها مهم‌تر هستند، اما دو گروه آخر هم تا حدی مورد بحث قرار خواهند گرفت.

فیلم آموزش ریاضی مهندسی – مرور و حل سوالات کنکور دکتری در فرادرس

کلیک کنید

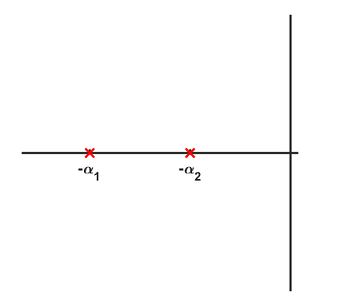
حالت ۱: سیستم تندمیرا ($$ \zeta > 1 $$)

در سیستم‌های تندمیرا، با مساوی صفر قرار دادن معادله مشخصه، تابع انتقال دارای دو قطب حقیقی خواهد بود که عبارتند از:

$$ s = - \zeta {\omega _0} \pm {\omega _0}\sqrt {{\zeta ^2} - 1} $$

برای راحتی به این قطب‌ها نام‌های $$ \alpha _1 $$ و $$ \alpha _2 $$ می‌دهیم:

$$ \begin{gathered} {\alpha _1} = \zeta {\omega _0} + {\omega _0}\sqrt {{\zeta ^2} - 1} = {\omega _0}\left( { \zeta + \sqrt {{\zeta ^2} - 1} } \right) \\
{\alpha _2} = \zeta {\omega _0} - {\omega _0}\sqrt {{\zeta ^2} - 1} = {\omega _0}\left( { \zeta - \sqrt {{\zeta ^2} - 1} } \right) \\ \end{gathered} $$

قطب‌ها را مانند تصویر زیر، در دیاگرام صفر و قطب رسم می‌کنیم.

همچنین باید توجه کنیم که:

$$ {\alpha _1} \cdot {\alpha _2} = {\omega _0}\left( { \zeta + \sqrt {{\zeta ^2} - 1} } \right) \cdot {\omega _0}\left( { \zeta - \sqrt {{\zeta ^2} - 1} } \right) \\
= \omega _0^2\left( {{\zeta ^2} + - \left( {{\zeta ^2} - 1} \right) + \zeta \sqrt {{\zeta ^2} - 1} - \zeta \sqrt {{\zeta ^2} - 1} } \right) = \omega _0^2 $$

تابع انتقال را می‌توان به صورت زیر نوشت:

$$ H(s) = K\frac{{\omega _0^2}}{{{s^2} + 2\zeta {\omega _0}s + \omega _0^2}} = K\frac{{{\alpha _1} \cdot {\alpha _2}}}{{\left( {s + {\alpha _1}} \right)\left( {s + {\alpha _2}} \right)}} $$

پاسخ پله واحد در حوزه فرکانس برابر است با:

$$ {Y_\gamma }(s) = \frac{1}{s}H(s) = \frac{1}{s}K\frac{{{\alpha _1} \cdot {\alpha _2}}}{{\left( {s + {\alpha _1}} \right)\left( {s + {\alpha _2}} \right)}} $$

حال با اعمال معکوس تبدیل لاپلاس روی معادله بالا، می‌توان به پاسخ پله واحد در حوزه زمان رسید:

$$ {y_\gamma }(t) = K\left( {1 - \frac{{{\alpha _2}{e^{ - \alpha_1 t}} - {\alpha _1}{e^{ - \alpha_2 t}}}}{{{\alpha _2} - {\alpha _1}}}} \right) $$

اگر معادله بالا را بر حسب ضریب میرایی و فرکانس طبیعی بازنویسی کنیم، به فرم زیر تبدیل خواهد شد:

$$ \begin{gathered}
{y_\gamma }(t) = K\left( {1 - \frac{{{\omega _0}\left( {\zeta - \sqrt {{\zeta ^2} - 1} } \right){e^{ - {\omega _0}\left( {\zeta + \sqrt {{\zeta ^2} - 1} } \right)t}} - {\omega _0}\left( {\zeta + \sqrt {{\zeta ^2} - 1} } \right){e^{ - {\omega _0}\left( {\zeta - \sqrt {{\zeta ^2} - 1} } \right)t}}}}{{{\omega _0}\left( {\zeta - \sqrt {{\zeta ^2} - 1} } \right) - {\omega _0}\left( {\zeta + \sqrt {{\zeta ^2} - 1} } \right)}}} \right) \\
= K\left( {1 + \frac{{\left( {\zeta - \sqrt {{\zeta ^2} - 1} } \right){e^{ - {\omega _0}\left( {\zeta + \sqrt {{\zeta ^2} - 1} } \right)t}} - \left( {\zeta + \sqrt {{\zeta ^2} - 1} } \right){e^{ - {\omega _0}\left( {\zeta - \sqrt {{\zeta ^2} - 1} } \right)t}}}}{{2\sqrt {{\zeta ^2} - 1} }}} \right) \\
\end{gathered} $$

این معادله نسبتا پیچیده است، اما چند نکته زیر در مورد آن اهمیت زیادی دارند:

فیلم آموزش ریاضی مهندسی – مرور و حل سوالات کنکور دکتری در فرادرس

کلیک کنید

مقدار نهایی زمانی که $$ t \rightarrow \infty $$ میل کند، برابر با $$ K $$ یا بهره سیستم خواهد شد. این مقدار همچنین با $$ H(0) $$ برابر است.
مقدار اولیه زمانی که $$ t \rightarrow 0 ^ + $$ میل کند، برابر با صفر خواهد بود. این مقدار همچنین با $$ H ( \infty ) $$ برابر است.
در فرمول بالا، هر کجا که $$ \omega _0 $$ حضور داشته باشد، حتما در $$ t $$ ضرب شده است. این بدین معنی است که هر وقت $$ \omega _0 $$ را دو برابر کنیم، سرعت سیستم دو برابر می‌شود، اما شکل پاسخ را تغییر نمی‌دهد، بلکه صرفا آن را در حوزه زمان بسط می‌دهد یا منقبض می‌کند.
زمانی که $$ \zeta \rightarrow \infty $$ میل کند، عبارت دوم در صورت کسر فوق، به سمت صفر میل می‌کند و سیستم مانند یک سیستم مرتبه اول رفتار می‌کند.

تاثیر $$ \zeta $$ و $$ \omega _0 $$ روی شکل پاسخ بعدا مورد بحث قرار می‌گیرند.

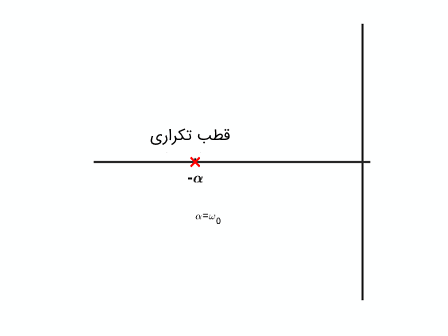
حالت ۲: سیستم میرای بحرانی ($$ \zeta = 1 $$)

برای به دست آوردن پاسخ پله واحد یک سیستم میرای بحرانی، روندی همانند سیستم تندمیرا را طی می‌کنیم. برای $$ \zeta = 1 $$، ریشه‌های مخرج کسر تابع انتقال سیستم، هر دو در $$ S = - \omega _0 $$ قرار دارند. همچنین محل ریشه‌ها را با $$ S = - \alpha $$ نیز نمایش می‌دهند. بنابراین می‌توان تابع انتقال سیستم را به صورت زیر بازنویسی کرد:

$$ H(s) = K\frac{{\omega _0^2}}{{{s^2} + 2{\omega _0}s + \omega _0^2}} = K\frac{{\omega _0^2}}{{{{\left( {s + {\omega _0}} \right)}^2}}} = K\frac{{{\alpha ^2}}}{{{{\left( {s + \alpha } \right)}^2}}} $$

این سیستم دارای قطب‌های تکراری در $$ S = - \omega _0 $$ است که در تصویر زیر نشان داده شده است.

پاسخ پله واحد این سیستم را در حوزه فرکانس می‌توان مانند فرمول زیر محاسبه کرد:

$$ {Y_\gamma }(s) = \frac{1}{s}H(s) = \frac{1}{s}K\frac{{\omega _0^2}}{{{{\left( {s + {\omega _0}} \right)}^2}}} = \frac{1}{s}K\frac{{{\alpha ^2}}}{{{{\left( {s + \alpha } \right)}^2}}} $$

حال با استفاده از معکوس تبدیل لاپلاس به معادله زیر برای پاسخ پله واحد در حوزه زمان دست می‌یابیم:

$$ \eqalign{ {y_\gamma }(t) &= K\left( {1 - {e^{ - {\omega _0}t}} - {\omega _0}t{e^{ - {\omega _0}t}}} \right) \\ &= K\left( {1 - {e^{ - \alpha t}} - {\omega _0}t{e^{ - \alpha t}}} \right) } $$

در مورد این پاسخ نیز می‌توان چند مشخصه بسیار مهم را به خاطر سپرد:

مقدار نهایی هنگامی که $$ t \rightarrow \infty $$ میل کند، برابر با $$ K $$ خواهد شد که همان بهره سیستم است. این مقدار همچنین با $$ H(0) $$ برابر است.
مقدار اولیه سیستم هنگامی که $$ t \rightarrow0 ^ + $$ میل کند، برابر با صفر خواهد شد که با $$ H ( \infty) $$ برابر است.
در معادله بالا، هر گاه که $$ \omega _0 $$ حضور داشته باشد، حتما در $$ t $$ ضرب می‌شود. این بدین معنی است که اگر $$ \omega _0 $$ را دو برابر کنیم، آن‌گاه سرعت سیستم نیز دو برابر می‌شود، اما شکل پاسخ تغییر نمی‌کند.
با دور شدن قطب‌ها از مبدا یا به عبارت دیگر با افزایش $$ \alpha $$، سرعت سیستم نیز افزایش می‌یابد.

حالت ۳: سیستم کندمیرا ($$ \zeta < 1 $$)

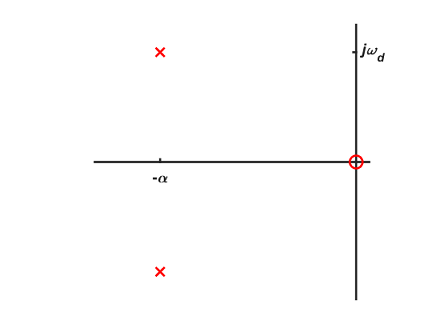
برای سیستم‌های کندمیرا، از تابع انتقال استفاده می‌کنیم تا پاسخ پله را در حوزه فرکانس یا حوزه لاپلاس به دست آوریم. محل قطب‌ها را می‌توان یا بر حسب $$ \omega _0 $$ و $$ \zeta $$ و یا بر حسب مقادیر حقیقی و موهومی آن‌ها ($$ \alpha $$ و $$ \omega _d $$) نوشت.

$$ H(s) = K \frac{{ \omega _0^2}}{{{s^2} + 2{ \omega _0} s + \omega _0^2 }} = K \frac {{{ \alpha ^2} + \omega _d^{^2}}}{{{{ \left( {s + \alpha } \right)}^2} + \omega _d^{^2 }}} $$

محل قطب‌ها در این سیستم را می‌توان در دیاگرام قطب زیر مشاهده کرد.

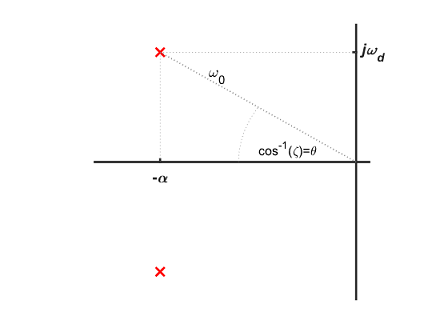
توجه کنید که $$ - \alpha $$ برابر با قسمت حقیقی قطب و $$ \pm j \omega _d $$ برابر با قسمت موهومی قطب است. همچنین می‌توان گفت که $$ \omega _0 $$ برابر با فاصله قطب از مبدا است و زاویه بین محور افقی و قطب را می‌توان از روی $$ \zeta $$ و با استفاده از فرمول $$ \theta = \cos ^ {-1} (\zeta) $$ به دست آورد. می‌توان این چهار مولفه را به صورت زیر به یکدیگر ربط داد:

$$ { \omega _d} = { \omega _0} \sqrt {1 - {\zeta ^2}} \\ $$

$$ \alpha = \zeta \omega _0 $$

در این حالت پاسخ پله سیستم برابر است با:

$$ {Y_\gamma }(s) = \frac {1} {s} H ( s ) = \frac {1} {s} K \frac {{\omega _0 ^ 2}}{{{s ^ 2} + 2{ \omega _0}s + \omega _0^2}} \\
= \frac {1} {s} K \frac {{{\alpha ^2} + \omega _d^{^2}}}{{{{\left( {s + \alpha } \right)}^2} + \omega _d^{^2}}} $$

حال با استفاده از تبدیل لاپلاس معکوس، می‌توانیم به رابطه پاسخ پله در حوزه زمان دست یابیم:

$$ {y_\gamma }(t) = K\left( {1 - \frac{1}{{\sqrt {1 - {\zeta ^2}} }}{e^{ - \zeta {\omega _0}t}}\sin \left( {{\omega _0} {\sqrt {1 - {\zeta ^2}} } t + \theta} \right)} \right) $$

$$ = K \left( {1 - \frac{\sqrt{{{\alpha ^2} + \omega _d^2}}}{{{\omega _d}}}{e ^{ - \alpha t}} \sin \left( {{\omega _d}t + \theta} \right)} \right) $$

$$ \theta = \operatorname{acos} \left( \zeta \right) = \operatorname{atan} \left( {\frac{{{\omega _d}}}{\alpha }} \right) $$

در تصویر زیر نمایی از پاسخ یک سیستم کندمیرا نشان داده شده است.

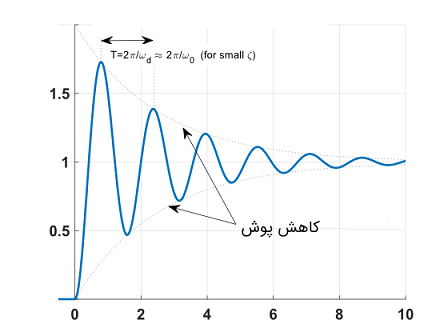
فرمول‌های بالا اطلاعات بسیار مهمی را در خود دارند. برخی از مهم‌ترین این اطلاعات عبارتند از:

فیلم آموزش ریاضی مهندسی – مرور و حل سوالات کنکور دکتری در فرادرس

کلیک کنید

مقدار نهایی در $$ t \rightarrow \infty $$، برابر با $$ K $$ است که همان بهره سیستم محسوب می‌شود. همچنین این مقدار با $$ H(0) $$ برابر است.
مقدار ابتدایی هنگامی که $$ t \rightarrow0^ + $$ میل کند، برابر با صفر است. این مقدار با $$ H ( \infty ) $$ برابر است.
در معادله بالا، هر گاه که $$ \omega _0 $$ حضور داشته باشد، حتما در $$ t $$ ضرب می‌شود. این بدین معنی است که اگر $$ \omega _0 $$ را دو برابر کنیم، آن‌گاه سرعت سیستم نیز دو برابر می‌شود، اما شکل پاسخ تغییر نمی‌کند. با افزایش مقدار $$ \omega _0 $$، سیستم سریع‌تر می‌شود و قطب‌ها از مبدا دور می‌شوند.
مقدار کاهشی $$ e^{ - \zeta {\omega _0} t} $$ دارای یک ضریب میرایی $$ \alpha = \zeta { \omega _0 } $$ است. به عبارت دیگر، می‌توان گفت که ثابت زمانی برابر با $$ \tau = \frac {1} {\zeta \omega _0} $$ به دست می‌آید.
فرکانس نوسان $$ \omega _d $$ را فرکانس میرایی (Damped Frequency) نیز می‌گویند که برابر است با $$ \omega _d = \omega _0 \sqrt{1 - \zeta ^ 2} $$.

بحث راجع به تاثیر $$ \zeta $$ و $$ \omega _0 $$ روی شکل پاسخ پله نیز بسیار مهم است که بعدا مورد بررسی قرار می‌گیرد.

حالت ۴: سیستم نامیرا ($$ \zeta = 0 $$)

زمانی که ضریب میرایی برابر با صفر باشد، اصطلاحا سیستم را نامیرا می‌گویند. ریشه‌های مخرج تابع انتقال برابر با $$ S = \pm J \omega $$ هستند، بنابراین تابع انتقال در حوزه لاپلاس برابر است با:

$$ H(s) = K\frac{{\omega _0^2}}{{{s^2} + \omega _0^2}} = K\frac{{\omega _0^2}}{{\left( {s + j{\omega _0}} \right)\left( {s - j{\omega _0}} \right)}} $$

بر اساس تابع فوق و تبدیل لاپلاس معکوس، پاسخ پله در حوزه زمان به صورت زیر نوشته می‌شود:

$$ {y_\gamma }(t) = K\left( {1 - \sin \left( {{\omega _0}t + \pi } \right)} \right) = K\left( {1 - \cos \left( {{\omega _0}t} \right)} \right) $$

همان طور که از نام این سیستم مشخص است، سیستم نامیرا هیچ میرایی یا نوسانی ندارد. در تصویر زیر نمایی از دیاگرام قطب‌های سیستم نامیرا نشان داده شده است.

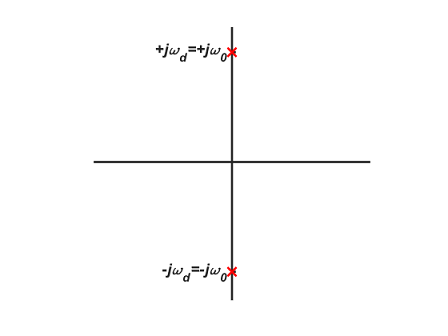
حالت ۵: رشد نمایی ($$ \zeta < 0 $$)

اگر حالتی را در نظر بگیریم که $$ \zeta < 0 $$ باشد، می‌توانیم تابع انتقال را بر حسب دو ریشه مخرج کسر آن بنویسیم:

$$ H(s) = K\frac{{\omega _0^2}}{{{s^2} + 2\zeta {\omega _0}s + \omega _0^2}} = K\frac{{{\alpha _1} \cdot {\alpha _2}}}{{\left( {s + {\alpha _1}} \right)\left( {s + {\alpha _2}} \right)}} $$

$$ {\alpha _1} = - \zeta {\omega _0} + {\omega _0}\sqrt {{\zeta ^2} - 1} = {\omega _0}\left( { - \zeta + \sqrt {{\zeta ^2} - 1} } \right) $$

$$ {\alpha _2} = - \zeta {\omega _0} - {\omega _0}\sqrt {{\zeta ^2} - 1} = {\omega _0}\left( { - \zeta - \sqrt {{\zeta ^2} - 1} } \right) $$

می‌توانیم پاسخ پله واحد را با ضرب کردن تابع انتقال $$ H(s) $$ در تبدیل لاپلاس پله واحد ($$ \frac {1} {S} $$) به دست آورد. فعلا فرض می‌کنیم که $$ \alpha _1 $$ و $$ \alpha _2 $$ با هم برابر نباشند:

$$ {Y_\gamma }(s) = \frac{1}{s}H(s) = \frac{1}{s}K\frac{{{\alpha _1} \cdot {\alpha _2}}}{{\left( {s + {\alpha _1}} \right)\left( {s + {\alpha _2}} \right)}} $$

$$ = \frac{{{A_1}}}{s} + \frac{{{A_2}}}{{s + {\alpha _1}}} + \frac{{{A_3}}}{{s + {\alpha _2}}} $$

$$ {y_\gamma }(t) = {A_1} + {A_2}{e^{ - {\alpha _1}t}} + {A_3}{e^{ - {\alpha _2}t}} $$

توجه کنید که مقادیر $$ A_1 $$ و $$ A_2 $$ و $$ A_3 $$ را در عبارات بالا محاسبه نکرده‌ایم، اما تعیین مقادیر دقیق آن‌ها در مقدار عبارت اهمیت زیادی ندارد؛ زیرا سیستم به صورت نمایی رشد می‌کند. چون قسمت حقیقی $$ \alpha _1 $$ و $$ \alpha _2 $$ اعداد منفی هستند، عبارت بالا با گذر زمان به صورت نمایی افزایش می‌یابد. همچنین به دلیل اینکه $$ \alpha _1 $$ و $$ \alpha _2 $$ اعداد مختلط هستند، عبارت بالا با گذر زمان نوسانی می‌شود. این رفتار در سیستم‌ها معمولا نادر است، اما در تئوری کنترل (Control Theory) چنین سیستم‌هایی از اهمیت بالایی برخوردار هستند. در تصویر زیر نمایی از دیاگرام قطب‌های یک سیستم ناپایدار یا رشد نمایی نشان داده شده است.

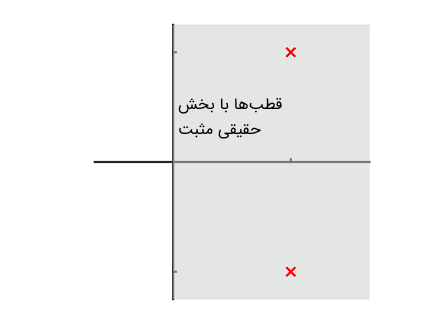
دیاگرام قطب‌های یک سیستم ناپایدار یا رشد نمایی

تاثیر بهره و $$ \zeta $$ و $$ \omega _0 $$ روی پاسخ پله پایین گذر سیستم درجه دوم

تابع انتقال سیستم پایین گذر درجه دوم را می‌توان توسط عبارت زیر نمایش داد:

$$ {H_{LP}}\left( s \right) = {H_{0,LP}}\frac{{\omega _0^2}}{{{s^2} + 2\zeta {\omega _0}s + \omega _0^2}} $$

دیاگرام قطب‌های سیستم درجه دو پایین گذر در شکل زیر مشاهده می‌شود.

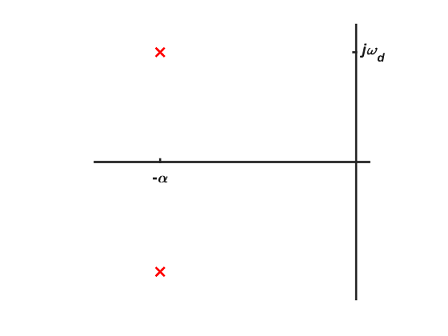
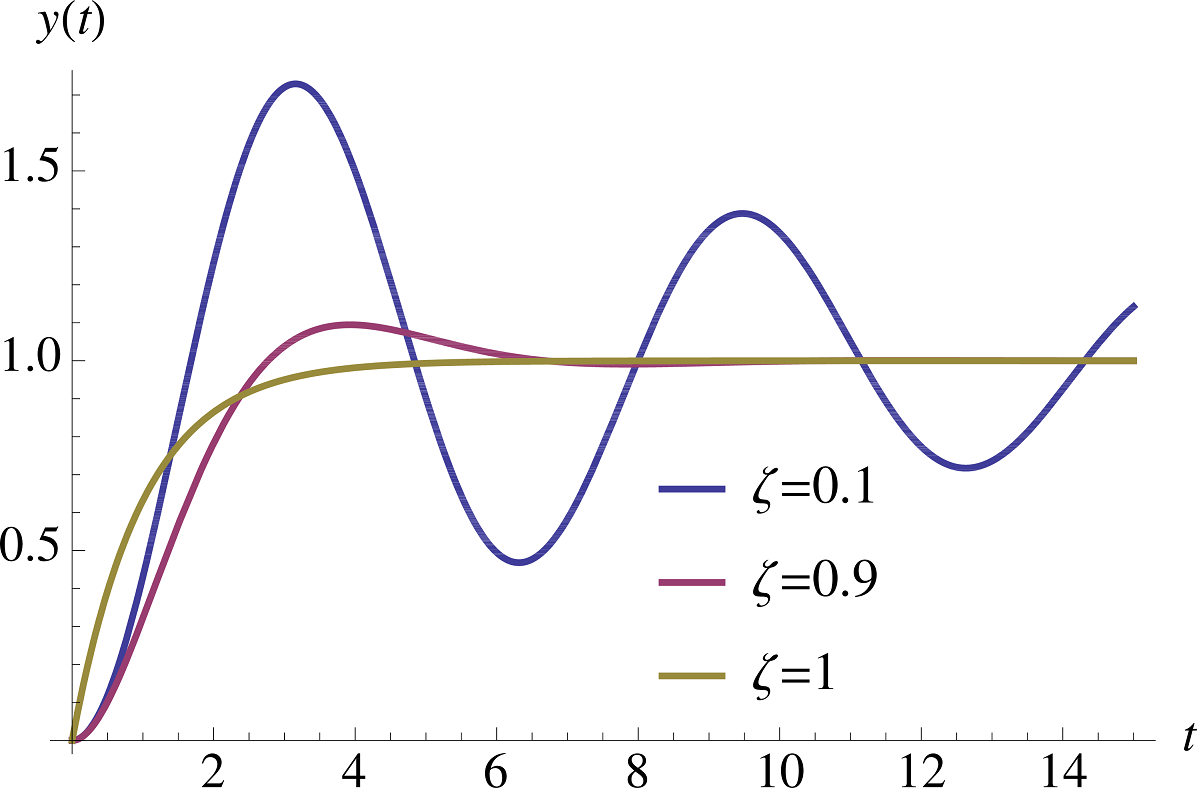
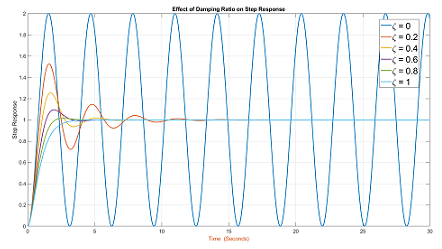
نمودار شکل زیر، تاثیر $$ \zeta $$ را روی پاسخ پله واحد یک سیستم درجه دو با مقادیر مثبت $$ \zeta $$ و $$ H_{0,LP}=1 $$ نمایش می‌دهد. برای $$ \zeta > 1 $$، سیستم تندمیرا خواهد شد و نوسان نمی‌کند. همچنین سیستم به ازای $$ \zeta = 1 $$ نیز نوسان نخواهد کرد. اما به ازای $$ \zeta < 1 $$، سیستم کندمیرا شده و هر چه به $$ \zeta \rightarrow 0 $$ نزدیک‌تر شود، بیشتر و بیشتر نوسان می‌کند.

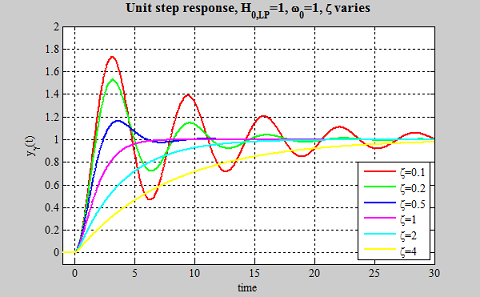
تصویر بالا تا زمانی که $$ \zeta > 0 $$ باشد، درست است. درباره این نمودار توجه به چند نکته بسیار مهم است:

فیلم آموزش تجزیه و تحلیل سیگنال ها و سیستم ها‎ در فرادرس

کلیک کنید

توجه کنید که میرایی بحرانی ($$ \zeta = 1 $$) هیچ رفتار غیر قابل پیش‌بینی را در سیستم به وجود نمی‌آورد. در واقع این حالت فقط از لحاظ ریاضی بسیار خاص است، اما روی رفتار فیزیکی سیستم تاثیری نخواهد گذاشت.
اگر $$ H_{0,LP} \neq 1 $$ باشد، پاسخ سیستم متناسب با آن مقیاس می‌شود. به عبارت دیگر، اگر $$ H_{0,LP} $$ دو برابر شود، دامنه پاسخ نیز دو برابر می‌شود.
مقدار اولیه ($$ t = 0 ^ + $$) را می‌توان از طریق $$ H ( \infty ) $$ به دست آورد، بنابراین $$ y _Y (0 ^ +) = 0 $$ خواهد شد.
مقدار نهایی ($$ t \rightarrow \infty $$) را می‌توان از روی $$ H ( 0 ) $$ و برابر با $$ y _Y (\infty) = 1 $$ به دست آورد.

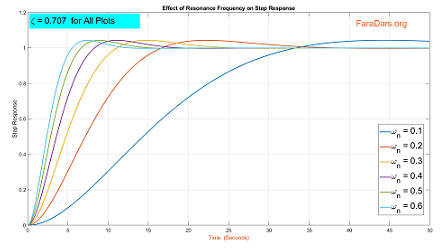
تصویر زیر تاثیر $$ \omega _0 $$ را روی پاسخ پله واحد یک سیستم درجه دوم نشان می‌دهد.

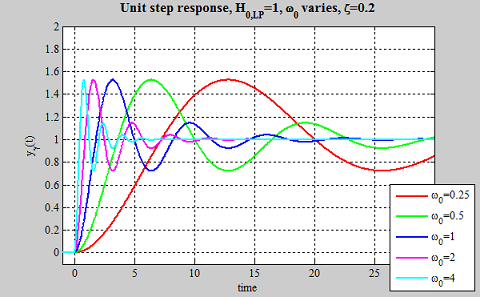
تاثیر $$ \omega _0 $$ روی پاسخ پله واحد یک سیستم درجه دوم

همان طور که از روی تصویر مشخص است، شکل پاسخ سیستم با تغییر $$ \omega _0 $$ ثابت باقی می‌ماند. اما سرعت سیستم تغییر می‌کند. البته به این نکته باید توجه کنید که دامنه پیک‌های اول، دوم، سوم و ... با یکدیگر برابر و از $$ \omega _0 $$ مستقل است و تنها با زمان تغییر می‌کند. هنگامی که $$ \omega _0 $$ افزایش می‌یابد، سرعت سیستم نیز افزایش می‌یابد. اگر $$ \omega _0 $$ دو برابر شود، سرعت سیستم نیز دو برابر می‌شود. اما باید به این نکته هم اشاره کرد که $$ \omega _0 $$ باعث ایجاد تغییر در شکل پاسخ نمی‌شود. زیرا $$ \omega _0 $$ و $$ t $$ همیشه با یکدیگر و به صورت جفت $$ \omega _0 . t $$ ظاهر می‌شوند. بنابراین افزایش $$ \omega _0 $$ باعث افزایش حاصل ضرب $$ \omega _0 . t $$ در هر لحظه از زمان نیز می‌شود.

تصویر زیر نیز نشان دهنده تاثیر $$ \zeta $$ روی پاسخ پله واحد سیستم درجه دوم به ازای مقادیر مثبت و منفی $$ \zeta $$ است.

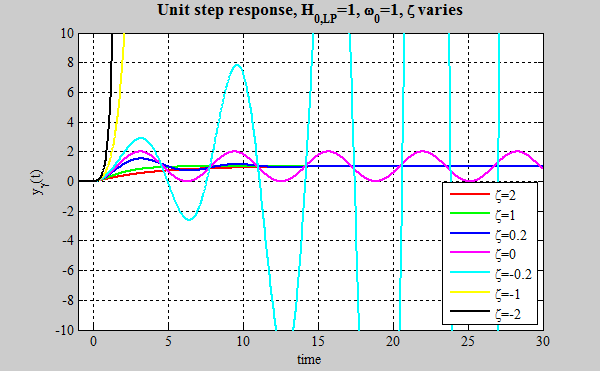
برای مقادیر مثبت $$ \zeta $$، پاسخ با زمان کاهش می‌یابد. به ازای $$ \zeta = 0 $$ سیستم هیچ میرایی نخواهد داشت و اصطلاحا سیستم نامیرا است. به ازای مقادیر منفی $$ \zeta $$ پاسخ با گذر زمان رشد خواهد کرد. در عمل ما زیاد با این سیستم‌ها برخورد نخواهیم کرد. اما در برخی موقعیت‌های خاص، این اتفاق برای سیستم رخ می‌دهد که به انرژی سیستم همواره افزوده می‌شود. توجه کنید که مقدار نهایی سیستم زمانی که $$ \zeta \leq 0 $$ باشد، تعریف نمی‌شود.

پاسخ پله سیستم مرتبه دو بالا گذر (Highpass)

سیستم مرتبه دو بالا گذر با معادله زیر توصیف می‌شود:

$$ {H_{HP}}\left( s \right) = {H_{0,HP}}\frac{{{s^2}}}{{{s^2} + 2\zeta {\omega _0}s + \omega _0^2}} $$

این سیستم دارای بسیاری از مشخصه‌های مشابه با سیستم مرتبه دوم پایین گذر است، اما تفاوت‌هایی نیز دارد. در تصویر زیر محل قطب‌ها در یک سیستم مرتبه دوم بالا گذر نشان داده شده است.

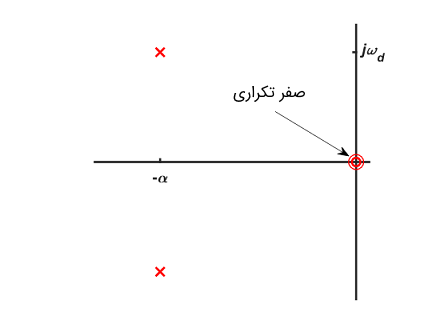
محل قطب‌ها در یک سیستم مرتبه دوم بالا گذر

در تصویر زیر نیز پاسخ پله یک سیستم مرتبه دوم بالا گذر نشان داده شده است.

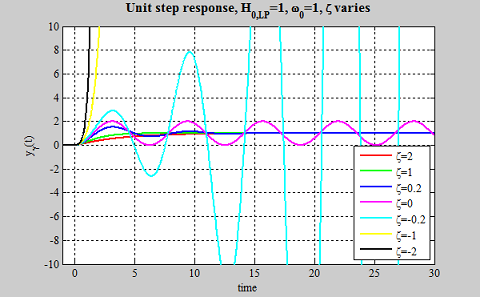
شباهت‌های سیستم‌های مرتبه دوم بالا گذر و پایین گذر عبارتند از:

زمانی که $$ \zeta $$ کاهش یابد، از نوسانی بودن سیستم کاسته می‌شود.
هنگامی که $$ \omega _ 0 $$ افزایش یابد، سیستم سریع‌تر می‌شود.
اگر $$ H _ {0,HP} \neq 1 $$ باشد، پاسخ متناسب با آن مقیاس می‌شود. اگر $$ H _ {0,HP} $$ دو برابر شود، دامنه پاسخ دو برابر می‌شود.

اما این دو سیستم با یکدیگر در موارد زیر متفاوت هستند:

مقدار اولیه در $$ t = 0^ + $$ بر اساس $$ H ( \infty ) $$ به دست می‌آید، اما اکنون $$ y _Y (0^ +) = H ( \infty ) = 1 $$ است.
مقدار نهایی در $$ t \rightarrow \infty $$ هنوز بر اساس $$ H ( 0 ) $$ تعیین می‌شود، اما اکنون $$ y _Y ( \infty) = H ( 0 ) = 0 $$ است. این مورد روی دیاگرام قطب و صفر با یک صفر در مبدا نشان داده می‌شود.

پاسخ پله سیستم مرتبه دوم میان گذر (Bandpass)

سیستم مرتبه دوم میان گذر نیز دارای بسیار مشخصه‌های مشابه با سیستم مرتبه دو پایین گذر و بالا گذر است. البته تفاوت‌هایی نیز با این دو سیستم دارد. این سیستم را می‌توان به صورت زیر نمایش داد:

$$ {H_{BP}}\left( s \right) = {H_{0,BP}}\frac{{2\zeta {\omega _0}s}}{{{s^2} + 2\zeta {\omega _0}s + \omega _0^2}} $$

محل قطب‌ها در یک سیستم مرتبه دو میا‌ن گذر در تصویر زیر نشان داده شده است.

شباهت‌های این سیستم با دو سیستم مرتبه دو بالا گذر و پایین گذر عبارت است از:

هنگامی که $$ \zeta $$ کاهش می‌یابد، سیستم کمتر میرا و بیشتر نوسانی می‌شود.
هنگامی که $$ \omega _ 0 $$ افزایش می‌یابد، سیستم سریع‌تر می‌شود.
اگر $$ H_{0,BP} \neq 1 $$ باشد، پاسخ سیستم متناسب با آن مقیاس می‌شود. به عبارت دیگر، اگر $$ H_{0,BP} $$ دو برابر شود، دامنه پاسخ دو برابر می‌شود.

اما سیستم مرتبه دو میان گذر با دو سیستم بالا گذر و پایین گذر در موارد زیر تفاوت دارد:

مقدار اولیه $$ t = 0^+ $$ هنوز بر اساس $$ H (\infty ) $$ محاسبه می‌شود، اما این بار $$ y_Y(0 ^ +) = H (\infty ) = 0 $$ است.
مقدار نهایی در $$ t \rightarrow \infty $$ هنوز هم بر اساس $$ H ( 0 ) $$ محاسبه می‌شود، اما اکنون $$ y_Y( \infty ) = 0 $$ است. این مورد روی نمودار صفر و قطب با صفر در مبدا نشان داده شده است.
$$ H_ {BP} (S = j \omega _0 ) = H _{0,BP} $$ در $$ \omega = \omega _0 $$ برقرار است.

پاسخ پله در متلب

در برنامه متلب زیر، تاثیر ضریب میرایی روی پاسخ پله یک سیستم مرتبه دوم نشان داده شده است.

فیلم آموزش پردازش سیگنال های واقعی در متلب در فرادرس

کلیک کنید

1clc;
2clear;
3close all;
4warning off;
5%%%  this app: the effect of damping ratio on step response of
6%%%  a second order system
7%%%  writer: Faradars.org, marzieh aghaei
8%% 
9T0 = 0 ; %% initial time
10Tf = 30 ;  %% final time
11Ts = 0.01 ; %% sample time
12t = T0:Ts:Tf ; % time vector
13s = tf('s') ; %% define s as  differentiation operator
14zeta = 0:0.2:1 ;   %% define  damping ratio   values
15wn = 2 ; 
16y = zeros(numel(zeta) ,size(t , 2));
17
18for i = 1:numel(zeta)
19    
20    system = wn^2/(s^2+2*zeta(i)*wn*s+wn^2) ;  %% define transfer function for a specific zeta
21    y(i , :) = step(system , t);  %% calculate  step response
22    
23end
24
25figure1 = figure('Color',[1 1 1]);
26
27% Create axes
28axes1 = axes('Parent',figure1);
29hold(axes1,'on');
30
31% Create multiple lines using matrix input to plot
32plot1 = plot(t,y,'LineWidth',2,'Parent',axes1);
33set(plot1(1),'DisplayName','\zeta = 0');
34set(plot1(2),'DisplayName','\zeta = 0.2');
35set(plot1(3),'DisplayName','\zeta = 0.4');
36set(plot1(4),'DisplayName','\zeta = 0.6');
37set(plot1(5),'DisplayName','\zeta = 0.8');
38set(plot1(6),'DisplayName','\zeta = 1');
39
40% Create ylabel
41ylabel('Step Response');
42
43% Create xlabel
44xlabel('Time  (Seconds)',...
45    'Color',[0.850980392156863 0.329411764705882 0.101960784313725]);
46
47% Create title
48title('Effect of Damping Ratio on Step Response');
49
50box(axes1,'on');
51grid(axes1,'on');
52% Set the remaining axes properties
53set(axes1,'FontSize',14);
54% Create legend
55legend1 = legend(axes1,'show');
56set(legend1,...
57    'Position',[0.799374731807758 0.634097531524633 0.0944372556072312 0.27565501383038],...
58    'FontSize',24);

تصویر زیر درخروجی این برنامه ترسیم می‌شود.

تاثیر ضریب میرایی روی پاسخ پله یک سیستم مرتبه دوم

در برنامه متلب زیر نیز تاثیر فرکانس پاسخ نامیرا روی پاسخ پله سیستم مرتبه دوم را بررسی می‌کنیم.

1clc;
2clear;
3close all;
4warning off;
5%%%  this app: the effect of undamped resonance frequency on 
6%%%  step response of a second order system
7%%%  writer: Faradars.org, marzieh aghaei
8%% 
9T0 = 0 ; %% initial time
10Tf = 50 ;  %% final time
11Ts = 0.01 ; %% sample time
12t = T0:Ts:Tf ; % time vector
13s = tf('s') ; %% define s as  differentiation operator
14zeta = 0.707 ; %% fixed  damping ratio  
15wn = 0.1:0.1:0.6 ; %% define  resonance frequency values
16
17y = zeros(numel(wn) ,size(t , 2));
18
19for i = 1:numel(wn)
20    
21    system = wn(i)^2/(s^2+2*zeta*wn(i)*s+wn(i)^2) ;  %% define transfer function for a specific zeta
22    y(i , :) = step(system , t);  %% calculate  step response
23    
24end
25
26% Create figure
27figure1 = figure('Color',[1 1 1]);
28
29% Create axes
30axes1 = axes('Parent',figure1);
31hold(axes1,'on');
32
33% Create multiple lines using matrix input to plot
34plot1 = plot(t,y,'LineWidth',2,'Parent',axes1);
35set(plot1(1),'DisplayName','\omega_n = 0.1');
36set(plot1(2),'DisplayName','\omega_n = 0.2');
37set(plot1(3),'DisplayName','\omega_n = 0.3');
38set(plot1(4),'DisplayName','\omega_n = 0.4');
39set(plot1(5),'DisplayName','\omega_n = 0.5');
40set(plot1(6),'DisplayName','\omega_n = 0.6');
41
42% Create ylabel
43ylabel('Step Response');
44
45% Create xlabel
46xlabel('Time  (Seconds)',...
47    'Color',[0.850980392156863 0.329411764705882 0.101960784313725]);
48
49% Create title
50title('Effect of Resonance Frequency on Step Response');
51
52box(axes1,'on');
53grid(axes1,'on');
54% Set the remaining axes properties
55set(axes1,'FontSize',14);
56% Create legend
57legend1 = legend(axes1,'show');
58set(legend1,...
59    'Position',[0.795708011440955 0.139647873665713 0.108020696340835 0.367358067865976],...
60    'FontSize',24);
61
62% Create textbox
63annotation(figure1,'textbox',...
64    [0.759379042690817 0.819960699243053 0.136481241914619 0.090519650101922],...
65    'Color',[1 0.411764705882353 0.16078431372549],...
66    'String','FaraDars.org',...
67    'FontSize',24,...
68    'FitBoxToText','off',...
69    'EdgeColor',[1 1 1]);
70
71% Create textbox
72annotation(figure1,'textbox',...
73    [0.133247089262617 0.86353711790393 0.213454075032338 0.0579519650654984],...
74    'String','\zeta = 0.707  for All Plots',...
75    'LineStyle',':',...
76    'FontSize',24,...
77    'FitBoxToText','off',...
78    'EdgeColor',[1 1 1],...
79    'BackgroundColor',[0 1 1]);

خروجی این برنامه در تصویر زیر نشان داده شده است.

تاثیر فرکانس پاسخ نامیرا روی پاسخ پله سیستم مرتبه دوم

در برنامه متلب زیر نیز تاثیر ثابت زمانی روی پاسخ پله سیستم مرتبه دو را بررسی می‌کنیم.

فیلم آموزش پردازش سیگنال های واقعی در متلب در فرادرس

کلیک کنید

1clc;
2clear;
3close all;
4warning off;
5%%%  this app: the effect of time constant on 
6%%%  step response of a first order system
7%%%  writer: Faradars.org, marzieh aghaei
8%% 
9T0 = 0 ; %% initial time
10Tf = 20 ;  %% final time
11Ts = 0.01 ; %% sample time
12t = T0:Ts:Tf ; % time vector
13s = tf('s') ; %% define s as  differentiation operator
14A = 1 ; %% fixed  DC gain  
15tau = 0.2:0.2:2 ; %% define time constants values
16
17y = zeros(numel(tau) ,size(t , 2));
18
19for i = 1:numel(tau)
20    
21    system = A/(tau(i)*s+1) ;     %% define transfer function for a specific zeta
22    y(i , :) = step(system , t);  %% calculate  step response
23    
24end
25
26% Create figure
27figure1 = figure('Color',[1 1 1]);
28
29% Create axes
30axes1 = axes('Parent',figure1);
31hold(axes1,'on');
32
33% Create multiple lines using matrix input to plot
34plot1 = plot(t,y,'LineWidth',2,'Parent',axes1);
35set(plot1(1),'DisplayName','\tau = 0.2');
36set(plot1(2),'DisplayName','\tau = 0.4');
37set(plot1(3),'DisplayName','\tau = 0.6');
38set(plot1(4),'DisplayName','\tau = 0.8');
39set(plot1(5),'DisplayName','\tau = 1');
40set(plot1(6),'DisplayName','\tau = 1.2');
41set(plot1(7),'DisplayName','\tau = 1.4');
42set(plot1(8),'DisplayName','\tau = 1.6');
43set(plot1(9),'DisplayName','\tau = 1.8');
44set(plot1(10),'DisplayName','\tau = 2');
45
46% Create ylabel
47ylabel('Step Response');
48
49% Create xlabel
50xlabel('Time  (Seconds)',...
51    'Color',[0.850980392156863 0.329411764705882 0.101960784313725]);
52
53% Create title
54title('Effect of Time Constant  on Step Response');
55
56box(axes1,'on');
57grid(axes1,'on');
58% Set the remaining axes properties
59set(axes1,'Color',[0.901960784313726 0.901960784313726 0.901960784313726],...
60    'FontSize',14);
61% Create legend
62legend1 = legend(axes1,'show');
63set(legend1,...
64    'Position',[0.812739193682002 0.123963854416353 0.0760416651920727 0.456877715918175],...
65    'FontSize',24,...
66    'Color',[1 1 1]);
67
68% Create textbox
69annotation(figure1,'textbox',...
70    [0.759379042690817 0.819960699243053 0.136481241914619 0.090519650101922],...
71    'Color',[1 0.411764705882353 0.16078431372549],...
72    'String','FaraDars.org',...
73    'FontSize',24,...
74    'FitBoxToText','off',...
75    'EdgeColor',[1 1 1]);
76
77% Create textbox
78annotation(figure1,'textbox',...
79    [0.573738680465724 0.126637554585152 0.217335058214745 0.100528384279472],...
80    'String',{'System = A/(\taus+1)','A = 0.707  for All Plots'},...
81    'LineStyle',':',...
82    'FontSize',24,...
83    'FitBoxToText','off',...
84    'EdgeColor',[1 1 1],...
85    'BackgroundColor',[0 1 1]);

خروجی این قطعه کد مطابق با تصویر زیر است.

تاثیر ثابت زمانی روی پاسخ پله سیستم مرتبه دو

در برنامه زیر تاثیر افزودن یک قطب در پاسخ پله سیستم مرتبه دو در متلب نشان داده شده است.

1clc;
2clear;
3close all;
4warning off;
5%%%  this app: the effect of additional pole on the 
6%%%  step response of a second order system
7%%%  writer: Faradars.org, marzieh aghaei
8%% 
9T0 = 0 ; %% initial time
10Tf = 10 ;  %% final time
11Ts = 0.01 ; %% sample time
12t = T0:Ts:Tf ; % time vector
13s = tf('s') ; %% define s as  differentiation operator
14zeta = 0.707 ;   %% define  damping ratio
15wn = 2 ;         %% define  resonance frequency
16AdditionalPole = 1:2:20;  %% define the location of additional pole
17y = zeros(numel(AdditionalPole) ,size(t , 2));
18
19for i = 1:numel(AdditionalPole)
20    
21    % define standard transfer function for a second order system
22    system = wn^2/(s^2+2*zeta*wn*s+wn^2) ;  
23    % add additional pole
24    system = system/(s/AdditionalPole(i)+1);
25    y(i , :) = step(system , t);  %% calculate  step response
26    
27end
28
29% Create figure
30figure1 = figure('Color',[1 1 1]);
31
32% Create axes
33axes1 = axes('Parent',figure1);
34hold(axes1,'on');
35
36% Create multiple lines using matrix input to plot
37plot1 = plot(t,y,'LineWidth',2,'Parent',axes1);
38set(plot1(1),'DisplayName','Pole = -1');
39set(plot1(2),'DisplayName','Pole = -3');
40set(plot1(3),'DisplayName','Pole = -5');
41set(plot1(4),'DisplayName','Pole = -7');
42set(plot1(5),'DisplayName','Pole = -9');
43set(plot1(6),'DisplayName','Pole = -11');
44set(plot1(7),'DisplayName','Pole = -13');
45set(plot1(8),'DisplayName','Pole = -15');
46set(plot1(9),'DisplayName','Pole = -17');
47set(plot1(10),'DisplayName','Pole = -19');
48
49% Create ylabel
50ylabel('Step Response');
51
52% Create xlabel
53xlabel('Time  (Seconds)',...
54    'Color',[0.850980392156863 0.329411764705882 0.101960784313725]);
55
56% Create title
57title('Effect of Additional Pole on Step Response of Second Order System');
58
59box(axes1,'on');
60grid(axes1,'on');
61% Set the remaining axes properties
62set(axes1,'FontSize',14);
63% Create legend
64legend1 = legend(axes1,'show');
65set(legend1,...
66    'Position',[0.760337835921071 0.124437719294577 0.121604137074439 0.456877715918174],...
67    'FontSize',24);
68
69% Create textbox
70annotation(figure1,'textbox',...
71    [0.141009055627426 0.830877731047082 0.247656242774489 0.0709606969005157],...
72    'String',{'\zeta = 0.707,   \omega_n = 2   for all plots'},...
73    'FontSize',24,...
74    'EdgeColor',[1 1 1]);
75
76% Create textbox
77annotation(figure1,'textbox',...
78    [0.575679172056922 0.601620088670191 0.263281242308828 0.0556768545612498],...
79    'String',{'The Location of Additional Poles:'},...
80    'FontSize',24,...
81    'EdgeColor',[1 1 1]);

خروجی این برنامه مطابق با تصویر زیر است.

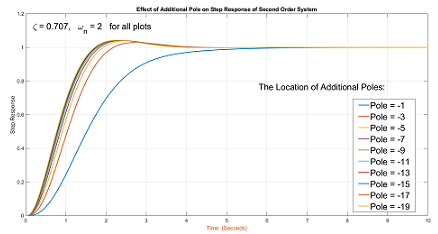
تاثیر افزودن یک قطب در پاسخ پله سیستم مرتبه دو

تاثیر افزودن صفر اضافه روی پاسخ پله سیستم مرتبه دوم در کد متلب زیر نشان داده شده است.

فیلم آموزش پردازش سیگنال های واقعی در متلب در فرادرس

کلیک کنید

1clc;
2clear;
3close all;
4warning off;
5%%%  this app: the effect of additional zero on the 
6%%%  step response of a second order system
7%%%  writer: Faradars.org, marzieh aghaei
8%% 
9T0 = 0 ; %% initial time
10Tf = 6 ;  %% final time
11Ts = 0.01 ; %% sample time
12t = T0:Ts:Tf ; % time vector
13s = tf('s') ; %% define s as  differentiation operator
14zeta = 0.707 ;   %% define  damping ratio
15wn = 2 ;         %% define  resonance frequency
16AdditionalZero = -0.1:0.02:0.1;  %% define the location of additional zero
17y = zeros(numel(AdditionalZero) ,size(t , 2));
18
19for i = 1:numel(AdditionalZero)
20    
21    % define standard transfer function for a second order system
22    system = wn^2/(s^2+2*zeta*wn*s+wn^2) ;  
23    % add additional pole
24    system = system*(s*AdditionalZero(i)+1);
25    y(i , :) = step(system , t);  %% calculate  step response
26    
27end
28
29% Create figure
30figure1 = figure('Color',[1 1 1]);
31
32% Create axes
33axes1 = axes('Parent',figure1);
34hold(axes1,'on');
35
36% Create multiple lines using matrix input to plot
37plot1 = plot(t,y,'LineWidth',2,'Parent',axes1);
38set(plot1(1),'DisplayName','ZeroTimeConstant = -0.10');
39set(plot1(2),'DisplayName','ZeroTimeConstant = -0.08');
40set(plot1(3),'DisplayName','ZeroTimeConstant = -0.06');
41set(plot1(4),'DisplayName','ZeroTimeConstant = -0.04');
42set(plot1(5),'DisplayName','ZeroTimeConstant = -0.02');
43set(plot1(6),'DisplayName','ZeroTimeConstant = -0.00');
44set(plot1(7),'DisplayName','ZeroTimeConstant = +0.02');
45set(plot1(8),'DisplayName','ZeroTimeConstant = +0.04');
46set(plot1(9),'DisplayName','ZeroTimeConstant = +0.06');
47set(plot1(10),'DisplayName','ZeroTimeConstant = +0.08');
48set(plot1(11),'DisplayName','ZeroTimeConstant = +0.10');
49
50% Create ylabel
51ylabel('Step Response');
52
53% Create xlabel
54xlabel('Time  (Seconds)',...
55    'Color',[0.850980392156863 0.329411764705882 0.101960784313725]);
56
57% Create title
58title('Effect of Additional Pole on Step Response of Second Order System');
59
60box(axes1,'on');
61grid(axes1,'on');
62% Set the remaining axes properties
63set(axes1,'FontSize',14);
64% Create legend
65legend1 = legend(axes1,'show');
66set(legend1,...
67    'Position',[0.666604682118126 0.115977021271593 0.226041660721724 0.502183391440122],...
68    'FontSize',24);
69
70% Create textbox
71annotation(figure1,'textbox',...
72    [0.141009055627426 0.830877731047082 0.33764553686934 0.0709606969005157],...
73    'String',{'\zeta = 0.707,   \omega_n = 2   for all plots'},...
74    'FontSize',24,...
75    'FitBoxToText','off',...
76    'EdgeColor',[1 1 1]);
77
78% Create textbox
79annotation(figure1,'textbox',...
80    [0.524026385295387 0.642013101770626 0.368161114704613 0.0556768545612499],...
81    'String',{'The Location of Additional Zero Time Constants:'},...
82    'FontSize',24,...
83    'FitBoxToText','off',...
84    'EdgeColor',[1 1 1]);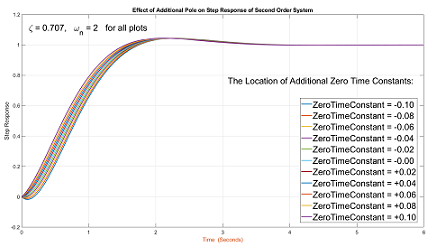

تاثیر افزودن صفر اضافه روی پاسخ پله سیستم مرتبه دوم

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

بر اساس رای ۸ نفر

آیا این مطلب برای شما مفید بود؟

اگر بازخوردی درباره این مطلب دارید یا پرسشی دارید که بدون پاسخ مانده است، آن را از طریق بخش نظرات مطرح کنید.

ثبت نظر

منابع:

swarthmore MIT

مرضیه آقایی (+)

«مرضیه آقایی» دانش‌آموخته مهندسی برق است. فعالیت‌های کاری و پژوهشی او در زمینه کنترل پیش‌بین موتورهای الکتریکی بوده و در حال حاضر، آموزش‌های مهندسی برق مجله فرادرس را می‌نویسد.