پاسخ سیستم مرتبه دوم — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

در ادامه مجموعه آموزش‌های سیستم‌های کنترل در مجله فرادرس، در این آموزش پاسخ سیستم مرتبه دوم را بررسی می‌کنیم. همچنین با اثر افزودن صفر و قطب بر سیستم آشنا خواهیم شد.

قبلاً با نمایش توابع تبدیل در سیستم‌های کنترل آشنا شدیم. دیدیم که توابع تبدیل قطب‌های حقیقی یا مختلط دارند. شکل کلی تابع تبدیل یک سیستم مرتبه دوم به صورت زیر بیان می‌شود:

$$ \large \begin {align*}
H ( s ) & = \frac { \omega ^ 2 _ n } { s ^ 2 + 2 \zeta \omega _ n s + \omega ^ 2 _ n } ,
\end {align*} $$

که در آن:

• $$ \zeta > 0 $$ و $$ \omega_n > 0 $$ پارامترهایی در $$ \mathscr {R } _{>0} $$ هستند.
• مخرج تابع تبدیل، یک چندجمله‌ای یکین (Monic) است. پارامتر $$ \zeta $$، میرایی یا ضریب میرایی، و $$ \omega_n $$ فرکانس طبیعی نامیده می‌شوند.
• بهره DC تابع تبدیل $$ H(s) $$ (اگر وجود داشته باشد) برابر با $$1$$ است.

فیلم آموزش کنترل خطی با رویکرد حل مساله در فرادرس

کلیک کنید

ریشه‌های معادله درجه دوم مخرج تابع تبدیل، به صورت زیر هستند:

$$ \large \begin {align*}
s & = - \zeta \omega _ n \pm \omega _ n \sqrt { \zeta ^ 2 - 1 } \\
& = - \omega _ n \left ( \zeta \pm \sqrt { \zeta ^ 2 - 1 } \right ) .
\end {align*} $$

همان‌طور که می‌بینیم، با تغییر $$ \zeta $$، طبیعت قطب‌ها نیز تغییر خواهد کرد:

• اگر $$ \zeta > 1 $$، هر دو قطب حقیقی و منفی هستند.
• اگر $$ \zeta = 1 $$، دو قطب تکراری منفی وجود دارد.
• اگر $$ \zeta < 1 $$، با دو قطب مختلط $$ s = -\sigma \pm j \omega_d $$ مواجه خواهیم بود که بخش حقیقی آن منفی است و تساوی‌های $$ \sigma = \zeta \omega_n $$ و $$ \omega_d = \omega_n \sqrt{1-\zeta^2} $$ را داریم.

سه حالت بالا، به ترتیب، تُندمیرا (Overdamped)، میرای بحرانی (Critically Damped) و کُندمیرا (Underdamped) نامیده می‌شوند. اگر $$ \zeta = 0 $$ باشد، میرایی در سیستم نخواهد بود ($$ \omega_d = \omega_n $$).

تابع تبدیل سیستم کُندمیرای زیر را در نظر بگیرید:

$$ \large \begin {align*}
H ( s ) & = \frac { \omega ^ 2 _ n } { s ^ 2 + 2 \zeta \omega _ n s + \omega ^ 2 _ n } , \mbox { } \, \, \, \, \, \, \, \, \zeta < 1 .
\end{align*} $$

قطب‌های این سیستم، به صورت زیر هستند:‌

$$ \large \begin {align*}
s & = - \zeta \omega _ n \pm j \omega _ n \sqrt { 1 - \zeta ^ 2 } \\
& = - \sigma \pm j \omega _ d
\end{align*} $$

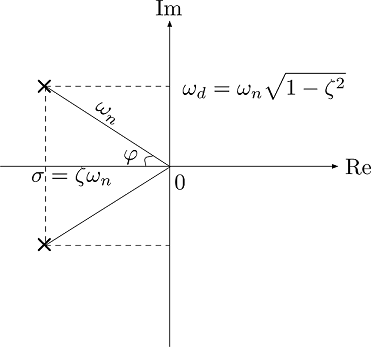
اگر مجذور قسمت‌های حقیقی و موهومی قطب‌ها را با هم جمع کنیم، به معادله یک دایره خواهیم رسید:

$$ \large \begin {align*}
\text {Re} ^ 2 + \text {Im} ^ 2 & = \omega _ n ^ 2 \left ( \zeta ^ 2 + \left ( \sqrt { 1 - \zeta ^ 2 } \right ) ^ 2 \right ) \\
& = \omega _ n ^ 2 .
\end{align*} $$

در شکل ۱، رابطه $$ \cos\varphi = \frac{\zeta\omega_n}{\omega_n} = \zeta $$ نیز برقرار است.

پاسخ ضربه سیستم به صورت زیر قابل محاسبه است:‌

\begin{align*} \large
h(t) & = \mathscr { L } ^ { - 1 } \{ H ( s ) \} \hspace{5.5cm} \\
& = \mathscr { L } ^ { - 1 } \left\{ \frac { \omega ^ 2 _ n } { s ^ 2 + 2 \zeta \omega _ n s + \omega ^ 2 _ n } \right\} \\
& = \mathscr { L } ^{ - 1 } \left\{ \frac { \omega ^ 2 _ n } { ( s + \sigma ) ^ 2 + \omega ^ 2 _ d } \right\} \hspace{3cm} \\
& = \mathscr { L } ^ { - 1 } \left\{ \frac { ( \omega ^ 2 _ n /\omega _ d ) \omega _ d } { ( s + \sigma ) ^ 2 + \omega ^ 2 _ d } \right\} \\
& = \frac { \omega ^ 2 _ n } { \omega _ d } e ^ { -\sigma t } \sin ( \omega _ d t ) . \hspace {4.5cm}
\end{align*}

به طور مشابه، می‌توان پاسخ پله را به صورت زیر محاسبه کرد:‌

$$ \large
\begin {align*}
y ( t ) & = \mathscr { L } ^ { - 1 } \left\{ Y ( s ) \right\} \\
& = \mathscr { L } ^ { - 1 } \left\{ \frac { H ( s ) } { s } \right\} \hspace {6cm} \\
& = \mathscr { L } ^ { - 1 } \left\{ \frac{\sigma ^ 2 + \omega ^ 2 _ d } { s [ ( s + \sigma ) ^ 2 + \omega ^ 2 _ d ] } \right \} \hspace {3.5cm} \\
& = 1 - e ^ { - \sigma t } \left ( \cos ( \omega _ d t ) +
\frac { \sigma } { \omega _ d } \sin ( \omega _ d t ) \right ) . \qquad
\end{align*} $$

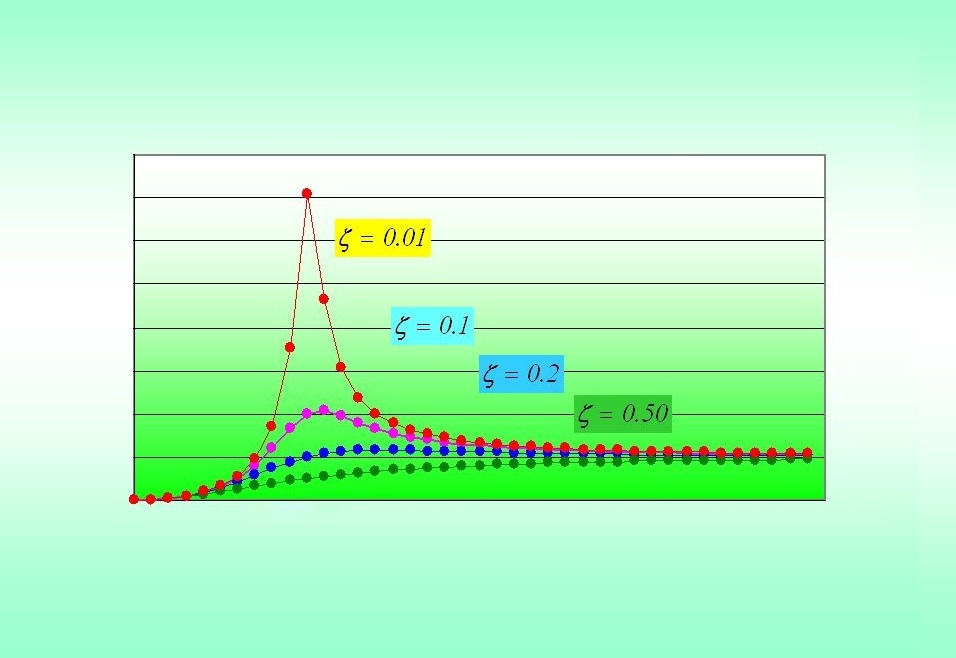
نمودار پاسخ پله سیستم مرتبه دوم کُندمیرا، برای مقادیر مختلف $$ \zeta $$ در شکل زیر نشان داده شده است.

با توجه به شکل بالا، نرخ میرایی نمایی پاسخ پله، به بخش حقیقی قطب‌های مختلط $$ \Re(s) = - \sigma = -\zeta \omega_n $$ بستگی دارد؛ در حالی که بخش موهومی، نوسانی بودن پاسخ را نشان می‌دهد. به همین دلیل است که $$ \omega_d = \omega_n \sqrt{1-\zeta^2} $$ فرکانس طبیعی میرا نامیده می‌شود.

همان‌طور که گفتیم، پاسخ پله تابع تبدیل سیستم مرتبه دوم کُندمیرایِ

$$ \large H ( s ) = \frac { \omega ^ 2 _ n } { s ^ 2 + 2 \zeta \omega _ n s + \omega ^ 2 _ n } = \frac { \omega ^ 2 _ n }{ ( s + \sigma ) ^ 2 + \omega ^ 2 _ d } $$

به صورت زیر است:

$$ \large y ( t ) = 1 - e ^ { - \sigma t } \left ( \cos ( \omega _ d t ) + \frac { \sigma } { \omega _ d } \sin ( \omega _ d t ) \right ) $$

که در آن، $$ \sigma = \zeta \omega_n $$ و $$ \omega_d = \omega_n \sqrt{1-\zeta^2} $$ فرکانس طبیعی میرا است.

در ادامه، خواهیم دید که ضریب میرایی $$ \zeta $$ و فرکانس طبیعی $$ \omega _ n $$ ویژگی‌های مهمی از بخش گذرای پاسخ پله را تعیین می‌کنند.

مشخصات پاسخ سیستم در حالت گذرا

در این بخش، برخی ویژگی‌های مهم پاسخ گذرا را بیان می‌کنیم.

فیلم آموزش سیستم های کنترل خطی در فرادرس

کلیک کنید

زمان صعود

ابتدا یک سیستم مرتبه اول را در نظر بگیرید:

$$ \large \begin {align*}
H ( s ) = \frac { a } { s + a } , \,\, \, \, \, \, a > 0 .
\end {align*} $$

سیستم بالا، یک قطب پایدار $$ s = -a $$ دارد. با استفاده از قضیه مقدار نهایی، بهره DC سیستم، برابر با $$1 $$ به دست می‌آید.

پاسخ پله این سیستم را می‌توان به صورت زیر محاسبه کرد:‌

$$ \large \begin {align*}
y ( t ) & = \mathscr { L } ^ { - 1 } \{ Y ( s ) \} \\
& = \mathscr { L } ^ { - 1 } \left\{ H ( s ) \frac { 1} { s } \right\} \\
& = \mathscr { L } ^ { - 1 } \left\{ \frac { a } { s ( s + a ) } \right \} \\
& = \mathscr { L } ^ { - 1 } \left \{ \frac { 1 } { s } - \frac { 1 } { s+ a } \right \} \\
& = 1 ( t ) - e ^ { - a t } .
\end{align*} $$

زمان صعود (Rise Time) را به عنوان مدت زمانی تعریف می‌کنیم که طول می‌کشد تا پاسخ سیستم از $$ 10 \% $$ به $$ 90 \%$$ مقدار حالت ماندگار (پاسخ پله) برسد. زمان صعود را با $$ t _ r $$‌ نشان می‌دهند. شکل زیر، زمان صعود پاسخ پله یک سیستم مرتبه اول را نشان می‌دهد.

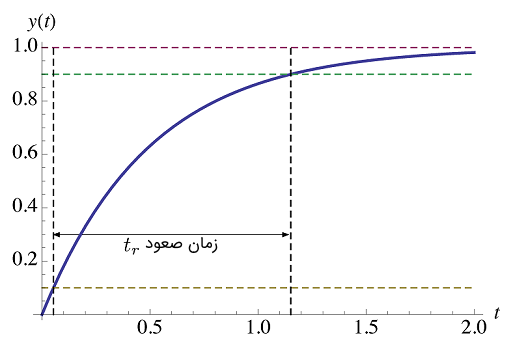
زمان صعود $$ t _ r $$ پاسخ پله $$ y(t) =1(t) - e^{-at} $$ را می‌توان به صورت تحلیلی و با استفاده از تعریف به دست آورد. فرض می‌کنیم $$ t_{0.1} $$ و $$ t_{0.9} $$، لحظاتی هستند که در پاسخ در آن‌ها، به ترتیب، به $$ 10 \%$$ و $$ 90 \%$$ مقدار حالت ماندگار می‌رسد (برای نخستین بار). در نتیجه، زمان صعود به صورت زیر به دست می‌آید:

$$ \large \begin {align*}
& 1 - e ^ { - a t _ { 0 . 1 } } = 0 . 1 , \qquad e ^ { -a t _ { 0 . 1 } } = 0 .9 , \qquad t _ { 0 .1 } = - \frac { \ln 0 . 9 } { a} ; \\
& 1 - e ^ { - a t _ { 0 . 9 } } = 0 . 9 , \qquad e ^ { -a t _ { 0. 9 } } = 0 . 1 , \qquad t _ { 0. 9 } = - \frac { \ln 0 . 1 } { a } . \\
& t _ r = t _ { 0 . 9 } - t _ { 0 . 1 } = \frac { \ln 0 . 9 - \ln 0 . 1 } { a } = \frac { \ln 9 } { a } \approx \frac { 2 . 2 } { a } .
\end {align*} $$

فراجهش و زمان نشست

اکنون به سیستم مرتبه دوم بر می‌گردیم. مجدداً سیستم مرتبه دوم کُندمیرای زیر را در نظر بگیرید:‌

$$ \large \begin {align*}
H ( s ) & = \frac { \omega ^ 2 _ n } { s ^ 2 + 2 \zeta \omega _n s + \omega ^ 2 _ n } = \frac { \omega ^ 2 _ n } { ( s + \sigma ) ^ 2 + \omega ^ 2 _ d } ,
\end{align*} $$

که در آن، $$ \sigma = \zeta \omega_n $$ و $$ \omega_d = \omega_n \sqrt{1-\zeta^2} $$ هستند و $$ \zeta < 1 $$ است.

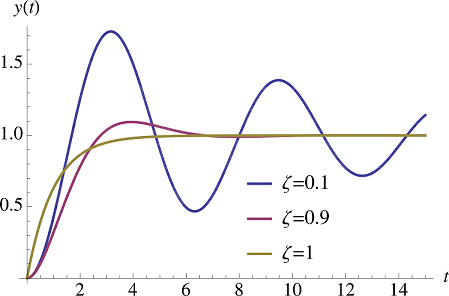
پاسخ پله $$ y ( t ) = 1 - e^ { - \sigma t } \left ( \cos ( \omega _ d
t ) + \dfrac { \sigma } { \omega _ d } \sin ( \omega _ d t ) \right ) $$ سیستم در شکل ۴ نشان داده شده است.

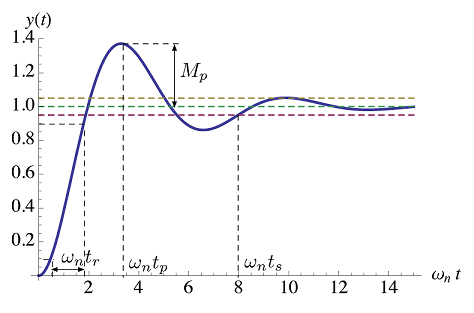
علاوه بر زمان صعود، دو ویژگی فراجهش (Overshoot) و زمان نشست (Settling Time) را نیز می‌توان بررسی کرد:

• زمان صعود $$t_r$$: مدت زمانی که $$ 0.1 y(\infty) $$ به $$ 0.9 y(\infty) $$ می‌رسد.
• فراجهش $$M_p$$ و زمان پیک $$t_p$$ ($$M_p$$ بر حسب درصد فراجهش نیز بیان می‌شود).
• زمان نشست $$ t_s$$: نخستین باری است که پاسخ گذرا به محدوده مشخص کوچکی از $$ y ( \infty ) $$ می‌رسد و در آن محدوده باقی می‌ماند. معمولاً محدوده $$5 \%$$ پاسخ حالت ماندگار را برای زمان نشست در نظر می‌گیریم. گفتنی است که مقدار پیش‌فرض برای محدوده تغییرات در تابع $$ \mathrm {stepinfo()}$$ نرم‌افزار متلب، $$2 \%$$ است.

در حالت کلی، وضعیت مطلوب برای پاسخی با صعود و نشست سریع و فراجهش کم، باید شرایط زیر را داشته باشد:

• $$ t _r$$ کوچک
• $$M_p$$ کوچک
• $$ t_p$$ کوچک
• $$ t_s$$ کوچک

اما در عمل، برآورده کردن همه شرایط فوق، ناممکن است، زیرا مثلاً کاهش $$t_r$$ به افزایش $$M_p$$ منجر می‌شود.

فرمول‌های مشخصات پاسخ در حوزه زمان

در این بخش، فرمول‌های مربوط به مشخصات پاسخ گذرا را بیان می‌کنیم.

فیلم آموزش کاربرد متلب در کنترل خطی در فرادرس

کلیک کنید

زمان صعود

در حالت کلی، محاسبه زمان صعود $$ t _ r$$ به صورت تحلیلی کار دشواری است؛ اما با نرمال کردن مقیاس زمان به صورت $$ t \to \omega_n t $$، می‌توان به صورت تجربی مقدار تقریبی زمان صعود را به دست آورد:

$$ \large w _ n t _ r \approx 1 . 8 . \qquad \text{( $\zeta = 0.5$)} $$

بنابراین، می‌توانیم از $$ t_r \approx \dfrac{1.8}{\omega_n} $$ استفاده کنیم که تقریب مناسبی برای $$ \zeta \approx 0.5 $$ است.

فراجهش و زمان پیک

در شکل ۴، زمان پیک $$ t_p$$ اولین لحظه‌ $$ t > 0$$‌ است که در آن، $$ y ^ \prime (t) =0 $$ برقرار است. پاسخ و مشتق آن به صورت زیر هستند:

$$ \large \begin{align*}
y ( t ) & = 1 - e ^ { -\sigma t } \left ( \cos ( \omega _ d t ) + \dfrac { \sigma } { \omega _ d } \sin ( \omega _ d t ) \right ) \\
y ^\prime ( t ) & = \left ( \frac { \sigma ^ 2 } { \omega _ d } + \omega _ d \right ) e ^ { - \sigma t } \sin ( \omega _ d t ) = 0, \text{ }\, \, \, \, \, \, \omega _ d t = 0 , \pi , 2 \pi , \ldots ,
\end {align*} $$

با استفاده از رابطه مشتق پاسخ و $$  y ^ \prime (t) =0  $$، زمان پیک، برابر است با $$ t_p = \dfrac{\pi}{\omega_d} $$.

برای محاسبه مقدار فراجهش $$ M_p $$، زمان پیک $$ t_p$$ را در معادله $$ y (t) $$‌ قرار می‌دهیم:

$$ \large \begin {align*}
M _ p & = y ( t _ p ) - 1 \\
& = - e ^ { - \frac { \sigma \pi } { \omega _ d } } \left ( \cos \left ( \omega _ d \frac { \pi } { \omega _ d } \right ) + \frac { \sigma } { \omega _ d } \sin \left ( \omega _ d \frac { \pi } { \omega _ d } \right ) \right ) \\
& = - \exp \left ( - \frac { \sigma \pi } { \omega _ d } \right ) ( - 1 + 0 ) \\
& = \exp \left ( - \frac { \pi \zeta } { \sqrt { 1 - \zeta ^ 2 } } \right ) .
\end{align*} $$

فرمول $$ M_p$$ دقیق است.

زمان نشست

زمان نشست، آخرین لحظه‌ای است که پاسخ پله به محدوده نوار خطای $$5\%$$ وارد می‌شود و از آن خارج نمی‌شود. بنابراین، می‌توان نوشت:

$$ \large t _ s = \min \left \{ t > 0 : \, \dfrac { | y ( t' ) - y ( \infty ) | } { y ( \infty ) }
\le 0 . 0 5 \text { for all } t' \ge t \right \} . $$

در شکل قبل، $$ y (\infty ) = 1 $$ است. بنابراین، نوار خطا را می‌توان به صورت زیر نوشت:

$$ \large \begin {align*}
| y ( t ) - 1 | & = e ^ { - \sigma t } \left | \cos ( \omega _ d t ) + \frac { \sigma } { \omega _ d } \sin ( \omega _ d t ) \right | ,
\end {align*} $$

که در آن، نمایی کاهشی $$ e^{-\sigma t} $$ همان جمله‌ای است که باید به آن توجه کنیم، زیرا توابع $$ \sin $$ و $$ \cos $$ به $$1$$ محدود هستند. بنابراین،  $$ e^{-\sigma t_s} \le 0.05 $$ منجر به رابطه $$ t_s = - \dfrac{\ln 0.05}{\sigma} \approx \dfrac{3}{\sigma} $$ خواهد شد.

به عنوان جمع‌بندی، برای مشخصات حوزه زمان یک سیستم مرتبه دوم کُندمیرایِ

$$ \large \begin {align*}
H ( s ) & = \frac { \omega ^ 2 _ n } { s ^ 2 + 2 \zeta \omega _ n s + \omega ^ 2 _ n} \\
& = \frac { \sigma ^ 2 + \omega _ d ^ 2 } { ( s + \sigma ) ^ 2 + \omega ^ 2 _ d } ,
\end {align*} $$

فرمول‌های زیر را داریم:

$$ \Large \begin {align*}
t _ r & \approx \frac { 1 . 8 } { \omega _ n } , \\
t _ p & = \frac { \pi } { \omega _ d } , \\
M _ p & = \exp \left ( - \frac { \pi \zeta } { \sqrt { 1 -\zeta ^ 2 } } \right ) , \\
t _ s & \approx \frac { 3 } { \sigma} .
\end {align*} $$

ارتباط مشخصات حوزه زمان و قطب‌ها در صفحه مختلط

با استفاده‌ از فرمول‌هایی که در بخش قبل برای یک سیستم مرتبه دوم کندمیرا گفته شد، می‌توان مشخصات حوزه زمان را با مکان قطب‌ها در صفحه مختلط نشان داد.

زمان صعود

فرض کنید می‌خواهیم رابطه $$ t_r \le c $$ برقرار باشد، که در آن، $$ c$$ کران بالای مطلوب برای زمان صعود است. در نتیجه، داریم:

$$ \large \begin {align*}
t _ r & \approx \dfrac { 1 . 8 } { \omega _n } \le c \\
\implies \omega _ n & \ge \dfrac { 1 . 8 } { c } .
\end {align*} $$

اگر رابطه بالا را به صورت هندسی بیان کنیم، قطب‌ها باید در ناحیه سایه زده شده شکل زیر قرار داشته باشند.

فراجهش

فرض کنید می‌خواهیم $$ M_p \le c $$ باشد:

$$ \large M _ p = { \exp \left ( -
\dfrac { \pi \zeta } { \sqrt { 1 -\zeta ^ 2 } } \right ) } \le c $$

به ضریب میرایی بزرگی نیاز داریم. طبق آنچه قبلاً گفتیم، می‌توان نوشت:

$$ \large \begin{align*}
\frac{\zeta}{\sqrt{1-\zeta^2}} &= \frac{\omega_n\zeta}{\omega_n\sqrt{1-\zeta^2}} \\
&= \frac{\sigma}{\omega_d} \\
&= \cot \varphi,
\end{align*} $$

بنابراین، $$ \varphi $$ باید کوچک باشد. اگر رابطه بالا را به صورت هندسی بیان کنیم، قطب‌ها باید در ناحیه سایه زده شده شکل زیر قرار داشته باشند.

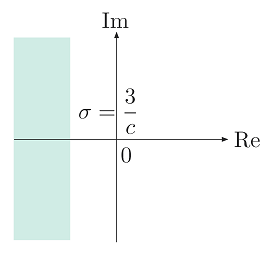
زمان نشست

فرض کنید می‌خواهیم $$ t_s \le c $$ باشد. بنابراین، داریم:

$$ \large \begin{align*}
t_s &\approx \dfrac{3}{\sigma} \le c \\
\implies &\sigma \ge \dfrac{3}{c}.
\end{align*} $$

در نتیجه، اندازه بخش حقیقی قطب‌ها ($$ {\rm Re}(s) = - \sigma $$) باید به اندازه کافی بزرگ باشد؛ یعنی به اندازه کافی از مبدأ دور باشد.

اگر رابطه بالا را به صورت هندسی بیان کنیم، قطب‌ها باید در ناحیه سایه زده شده شکل زیر قرار داشته باشند.

هرچه اندازه قطب‌های سمت چپ محور موهومی بزرگ‌تر باشند، پاسخ سریع‌تر و در نتیجه $$t _s $$ کوچک‌تر است.

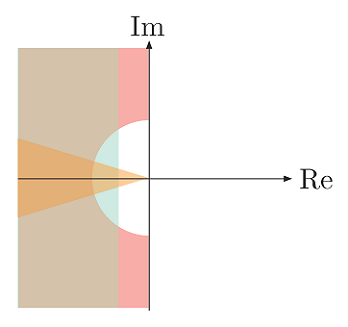
اگر قیود و الزاماتی که داریم، ترکیبی از ویژگی‌های $$ t_r$$، $$M_p$$ و $$ t _s $$ باشد، می‌توانیم به سادگی آن‌ها را بر صفحه مختلط اعمال کرده و اشتراک آن‌ها را به عنوان محدوده مجاز برای انتخاب قطب‌ها تعیین کنیم. شکل زیر این موضوع را نشان می‌دهد.

اثر صفر و قطب‌ بر پاسخ گذرا

در این بخش، اثر افزودن صفر‌ها و قطب‌ها را بر شکل پاسخ گذرا بررسی می‌کنیم.

فرض کنید تابع تبدیل سیستم، به صورت زیر باشد:‌

$$ \large H ( s ) = \dfrac { q ( s ) } { p ( s ) } $$

صفرهای این سیستم، ریشه‌های چندجمله‌ای صورت $$ q(s) = 0 $$ هستند.

فیلم آموزش سیستم های کنترل هوشمند در فرادرس

کلیک کنید

اثر صفر سمت چپ

این حالت را در قالب یک مثال توضیح می‌دهیم. تابع تبدیل $$ H_1 (s) $$ را با فرکانس طبیعی نرمال‌شده $$ \omega _ n = 1 \, \mathrm {rad/s}$$ در نظر بگیرید:

$$ \large H _ 1 ( s ) = \dfrac { 1 } { s ^ 2 + 2 \zeta s + 1 } , \text { } \, \, \, \, \, \omega _ n = 1 . $$

فرض می‌کنیم صفر جدید $$ s = - a $$ ( $$ a > 0 $$) به $$H_1 (s) $$ اضافه شود. برای آنکه بهره DC برابر با $$ 1 $$ باقی بماند، جمله ثابت صورت را به شکل نرمال $$ \dfrac{s}{a}+1 $$ در نظر می‌گیریم. تابع تبدیل جديد $$ H_2 (s)$$ به صورت زیر خواهد بود:

$$ \large \begin {align*}
H _ 2 ( s ) & = \frac { \frac { s } { a } + 1 } {s ^ 2 + 2 \zeta s + 1 } \\
& = \underbrace { \frac { 1 } { s ^ 2 + 2 \zeta s + 1 } } _ { \text { $ H _ 1 ( s ) $ } } + \frac { 1 } { a } \cdot \underbrace { \frac { s } { s ^ 2 + 2 \zeta s + 1 } } _ { \text { $ H _ d ( s ) $ } } \\
& = H _ 1 ( s ) + \frac { 1 } { a } H _ d ( s ) , \qquad H _ d ( s ) = s H _ 1 ( s ) .
\end{align*} $$

بنابراین، به طور خلاصه می‌توان گفت:

$$ \large \begin {align*}
H _ 1 ( s ) = \frac { 1 } { s ^ 2 + 2 \zeta s + 1 } \, \, \xrightarrow { \text {$ s = - a $}} \, \, H _ 2 ( s ) = H _ 1 ( s ) + \frac { 1 } { a } \cdot s H _ 1 ( s )
\end {align*} $$

اکنون رابطه بین پاسخ پله تابع تبدیل جدید $$ H_2 (s) $$ و تابع تبدیل اصلی $$ H_1 (s) $$ را به دست می‌آوریم. پاسخ پله دو تابع تبدیل به صورت زیر است:

$$ \large \begin {align*}
Y _ 1 ( s ) & = \frac { H_ 1 ( s ) } { s } ; \\
Y _ 2 ( s ) & = \frac { H _ 2 ( s ) } { s } \\
& = \frac { 1 } s \left ( H _ 1 ( s ) + \frac { 1 } { a } s H _ 1 ( s ) \right ) \\
& = \frac { H _ 1 ( s ) } { s } + \frac { 1 } a s \frac { H _ 1 ( s ) } s \\
& = Y _ 1 ( s ) + \frac { 1 } { a } s Y _ 1 ( s ) .
\end{align*} $$

بنابراین، با فرض شرایط اولیه صفر، داریم:

$$ \large \begin{align*}
y _ 2 ( t ) & = \mathscr { L } ^ { - 1 } \{ Y _ 2 ( s ) \} \\
& = \mathscr { L } ^ { - 1 } \left\{ Y _ 1 ( s ) + \frac { 1 } { a } \cdot s Y _ 1 ( s ) \right \} \\
& = y _ 1 ( t ) + \frac { 1 } { a } \dot { y } _ 1 ( t ) .
\end{align*} $$

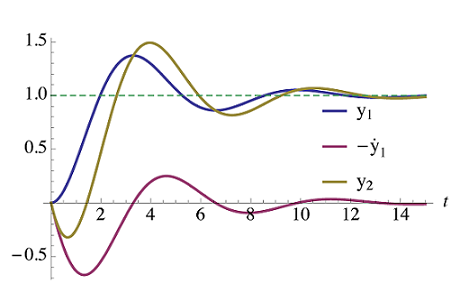
از معادله اخیر می‌توان دریافت که اضافه کردن صفر $$ s= -a$$ به تابع تبدیل اصلی، پاسخ جدید $$ y _2 (t) $$ را نتیجه خواهد داد که برابر با مجموع پاسخ اصلی $$ y _1 (t) $$ و ضریبی از مشتق $$ \dot{y}_1(t) $$ آن است.

$$ \large \begin{align*}
y _ 2 ( t ) & = y _ 1 ( t ) + \frac { 1 } a \dot { y } _1 ( t )
\end{align*} $$

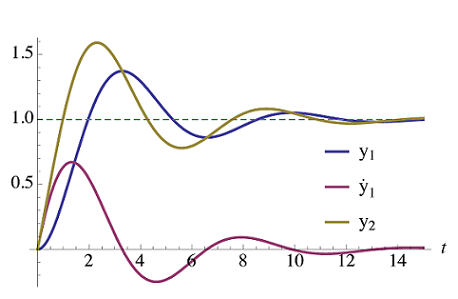
طبق شکل بالا، صفر سمت راست، سبب موارد زیر می‌شود:

• افزایش فراجهش (به عنوان اثر اصلی)؛
• کمی تغییر در زمان نشست؛
• و هرچه صفر از مبدأ دورتر باشد؛ یعنی $$ a \to \infty $$، اثر آن کمتر خواهد بود؛ زیرا $$ \frac{1}a \dot{y}_1(t) \to 0 $$.

اثر صفر سمت راست

مشابه بخش قبل، می‌توانیم اثر صفر سمت راست $$ s = a $$ ($$ a > 0 $$) را بر پاسخ سیستم بررسی کنیم. نتیجه افزودن صفر سمت راست به سیستم، به صورت زیر است:

$$ \large \begin {align*}
H _ 1 ( s ) = \frac { 1 } { s ^ 2 + 2 \zeta s + 1 } \, \, \xrightarrow { \text {$ s = a $} } \, \, H _ 2 ( s ) & = H _ 1 ( s ) - \frac { 1 } { a } \cdot s H _ 1 ( s ) , \\
y _ 2 ( t ) & = y _ 1 ( t ) - \frac { 1 } { a } \cdot \dot { y } _ 1 ( t ) .
\end {align*} $$

از معادله بالا می‌توان دریافت که اضافه کردن صفر $$ s=a$$ به تابع تبدیل اصلی، پاسخ جدید $$ y _2 (t) $$ را نتیجه خواهد داد که برابر با حاصل تفریق ضریبی از مشتق $$ \dot{y}_1(t) $$ از پاسخ اصلی $$ y _1 (t) $$ است.

طبق شکل بالا، می‌توان گفت که افزودن یک صفر سمت راست بر سیستم، سبب موارد زیر می‌شود:

• کند شدن یا تأخیر در پاسخ اصلی؛
• ایجاد فروجهش بزرگ، در صورت بسیار نزدیک بودن صفر به مبدأ.

اثر قطب سمت چپ

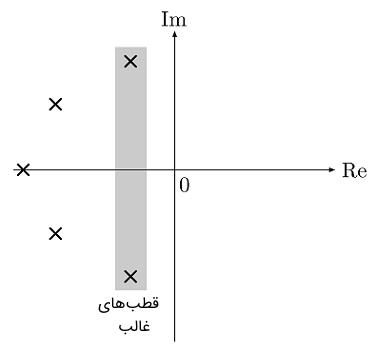
یک سیستم مرتبه $$n$$ عمومی، دارای $$n$$ قطب (مختلط) است، زیرا طبق قضیه اساسی جبر، معادله چندجمله‌ای $$ p(s) = 0 $$، دقیقاً $$ n $$ ریشه در مجموعه اعداد مختلط دارد. همچنین، می‌توان گفت:

• اگر بخش حقیقی قطب‌های سمت چپ حداقل $$5$$ برابر از بخش حقیقی قطب‌های غالب سمت چپ بزرگتر باشد، تأثیر زیادی نخواهند داشت. مثلاً اگر برای قطب‌های غالب، $$ {\rm Re}(s) = -2 $$ را داشته باشیم و بخش حقیقی قطب‌های اضافه، $$ {\rm Re}(s) = -10 $$ باشد، تأثیر آن‌ها در حوطه زمان، به ترتیب، $$ e^{-2t} $$ و $$ e^{-10t} $$ خواهد بود و با توجه به $$ e^{-10t} \ll e^{-2t} $$، تأثیر قطب‌های اضافه، قابل توجه نخواهد بود.
• $$5$$ برابر تنها یک قرارداد است؛ اما واقعاً می‌توان اثر قطب‌های نزدیک‌تر را مشاهده کرد.

اثر قطب سمت راست

بررسی اثر قطب‌های سمت راست بر سیستم توجیهی ندارد، زیرا این قطب‌ها ناپایدارند.

اثر قطب‌های روی محور موهومی

وضعیتی که قطب‌ها روی محور موهومی قرار دارند، یک حالت مرزی است. برای بررسی این مورد، ابتدا فرض کنید یک قطب در مبدأ داریم:

$$ \large H ( s ) = \dfrac { 1 } { s }  $$

آیا این سیستم پایدار است؟

• پاسخ ضربه، برابر با $$ Y(s) = \dfrac{1}{s} \implies y(t) = 1(t) $$ و یک تابع واحد و در نتیجه، پایدار است.
• پاسخ پله برابر با $$ Y(s) = \dfrac{1}{s^2} \implies y(t) = t, \, t\ge 0 $$ است. خروجی آن، یک شیب واحد است و افزایشی است.

اکنون حالتی را در نظر بگیرید که سیستم دو قطب موهومی دارد:

$$ \large H ( s ) = \dfrac { \omega ^ 2 } { s ^ 2 + \omega ^ 2 } . $$

• پاسخ ضربه، برابر با $$Y(s) = \dfrac{\omega^2}{s^2+\omega^2}
  \implies y(t) = \omega \sin (\omega t) $$ و خروجی محدود است، اما همگرا نمی‌شود.
• پاسخ پله برابر با $$ Y(s) = \dfrac{\omega^2}{s(s^2+\omega^2)}
  \implies y(t) = 1 - \cos(\omega t) $$ است و خروجی محدود است، اما همگرا نمی‌شود.

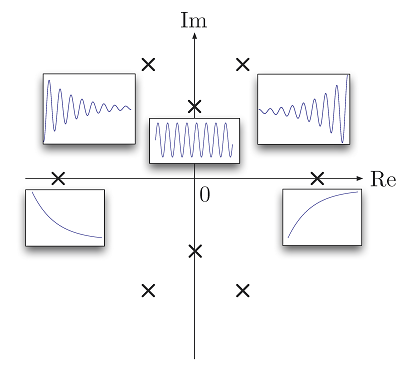
بنابراین، سیستم‌هایی با قطب روی محور موهومی، اکیداً پایدار نیستند. برای درک بهتر اثر قطب بر سیستم، شکل زیر را ببینید.

به طور خلاصه می‌توان گفت:

• پاسخ سیستم برای قطب‌هایی که بخش حقیقی آن‌ها در سمت چپ محور موهومی است ($$ {\rm Re}(s) < 0 $$)، پایدار است.
• پاسخ سیستم برای قطب‌هایی که بخش حقیقی آن‌ها در سمت راست محور موهومی است ($$ {\rm Re}(s) > 0 $$)، ناپایدار است.
• پاسخ سیستم برای قطب‌هایی که روی محور موهومی قرار دارند($$ {\rm Re}(s) = 0 $$)، اکیداً پایدار نیست.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• سیستم کنترل حلقه باز — به زبان ساده
• مکان هندسی ریشه ها (Root Locus) در مهندسی کنترل — به زبان ساده
• تقلب‌نامه (Cheat Sheet) تبدیل لاپلاس

^^

فیلم‌ های آموزش پاسخ سیستم مرتبه دوم — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

فیلم آموزشی سیستم مرتبه دوم

فیلم آموزشی پاسخ ضربه و پله سیستم مرتبه دوم

فیلم آموزشی زمان صعود و نشست پاسخ پله سیستم مرتبه دوم

فیلم آموزشی زمان پیک و درصد بالازدگی پاسخ پله

فیلم آموزشی ارتباط مشخصات حوزه زمان و قطب‌ها در صفحه مختلط

فیلم آموزشی اثر صفر و قطب‌ بر پاسخ پله