رزونانس – به زبان ساده

در طبیعت، رزونانس یا تشدید در موقعیتهای مختلفی رخ میدهد. هر سیستم مکانیکی تمایل دارد در برخی از فرکانسها، با بیشترین دامنه ممکن نوسان کند. به این وضعیت، رزونانس (تشدید) و به این فرکانسها، فرکانس رزونانس (فرکانس تشدید) گفته میشود. در حالت کلی، فرکانس تشدید همان فرکانس طبیعی سیستم است. رفتار سیستم در فرکانس رزونانس (یا نزدیک آن) به طرز عجیبی با رفتار سیستم در فرکانسهای دیگر متفاوت است. با وقوع پدیده رزونانس، ارتعاش ضعیف در یک جسم، میتواند منجر به ارتعاش قوی در جسم دیگری شود.
پدیده رزونانس در زندگی روزمره
پدیده رزونانس، همیشه اتفاق بدی به حساب نمیآید. کودکی را در نظر بگیرید که سوار تاب است و کسی هم او را هل نمیدهد. کودک شروع به تاب دادن خودش به سمت عقب و جلو میکند. اگر این کار را با فرکانس درستی انجام دهد، پس از مدت کوتاهی، مطابق شکل زیر، تاب با دامنه زیاد در حال جلو و عقب رفتن خواهد بود.
به این نکته توجه کنید که نیرویی که کودک در این فرآیند مصرف میکند، کوچک است. ولی نتیجه این عمل، دامنههای بزرگی را تشکیل میدهد.

به عنوان مثالی دیگر از این پدیده، پیچ تنظیم رادیو را در نظر بگیرید. با چرخاندن پیچ تنظیم، در واقع در حال تغییر فرکانس طبیعی مدار الکتریکی رادیو هستیم. هنگامی که این فرکانس طبیعی با فرکانس ایستگاه رادیویی مورد نظر یکسان شود، جذب انرژی به مقدار بیشینه میرسد و فقط صدای همان ایستگاه رادیویی را خواهیم شنید.
در سوی مقابل، رزونانس آثار مخرب بسیاری دارد. هنگامی که زلزله رخ میدهد، برخی ساختمانها فرو میریزند. در حالی که برخی دیگر از ساختمانها پابرجا ماندهاند. یکی از عوامل تعیین کننده در این فروپاشی، فرکانس رزونانس یا فرکانس طبیعی ساختمان است. اگر فرکانس ارتعاش زمین با فرکانس طبیعی ساختمان یکی شود، ساختمان بیشترین دامنه نوسان و شدیدترین خسارت را تجربه خواهد کرد. در سال 1940 میلادی پل «تاکوما ناروز» (Tacoma Narrows) در معرض بادی با سرعت 64 کیلومتر در ساعت قرار گرفت. یکی بودن فرکانس باد و فرکانس طبیعی پل موجب افزایش دامنه نوسان پل و در نهایت، تخریب آن شد.
مثال جرم و فنر زیر را در نظر بگیرید. معادله دیفرانسیل زیر را برای ارتعاش اجباری میتوان نوشت. در این رابطه، $$k$$ ثابت فنر، $$c$$ ضریب میرایی و $$m$$ جرم وزنهایست که نیروی خارجی $$F$$ به آن وارد شده است.
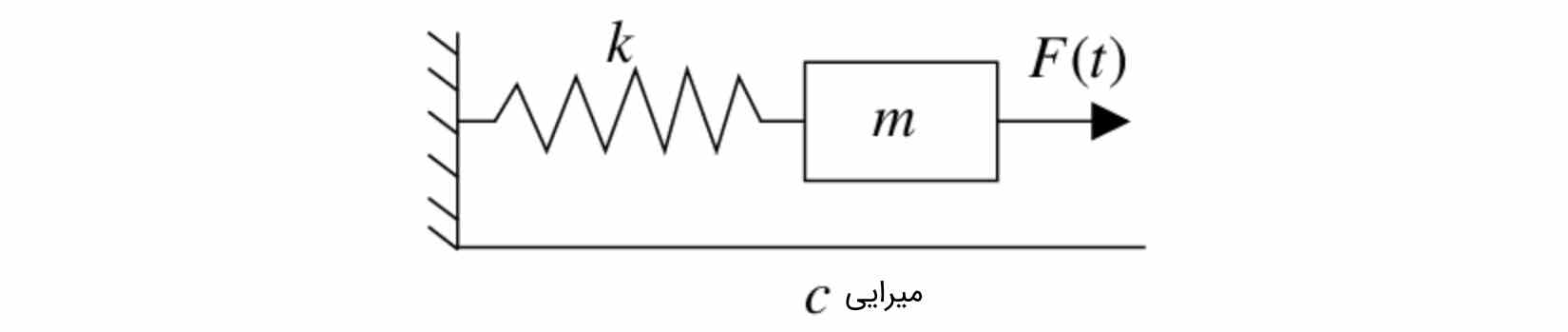
$$\large mx^{\prime\prime} + cx^{\prime} + kx = F(t)$$
پس از یادگیری سری فوریه میتوانیم برای تمام توابع نوسانی، عبارت $$\large F(t)= F_0\cos(\omega t)$$ را در نظر بگیرید. همچنین میتوان به جای کسینوس، از تابع سینوسی استفاده کرد. نتایج در هر دو حالت یکی است. ادامه تحلیل را در دو بخش زیر ادامه میدهیم.
محاسبه رزونانس در ارتعاش اجباری نامیرا
در این حالت برای سادگی، ارتعاش را نامیرا فرض میکنیم. با جایگذاری $$c=0$$ معادله حرکت به صورت زیر ساده میشود.
$$\large mx^{\prime\prime} + kx = F_0\cos(\omega t)$$
پاسخ عمومی معادله بالا به صورت زیر به دست میآید.
$$\large x_c=C_1\cos(\omega_nt)+C_2\sin(\omega_nt)$$
در این رابطه، $$\large \omega_n=\sqrt{\frac{k}{m}}$$ فرکانس طبیعی سیستم است. فرکانس طبیعی، فرکانسی است که سیستم تمایل دارد در غیاب نیروی خارجی نوسان کند. فرض میکنیم $$\large \omega_n\neq\omega$$ و با استفاده از $$\large x_p=A\cos(\omega t)$$ معادله را برای $$A$$ حل میکنیم. با استفاده از روش ضرایب نامعین، جواب خصوصی به صورت زیر حاصل میشود.
$$\large x_p=\frac{F_0}{m({\omega_n}^2-\omega^2)}\cos(\omega t)$$
در نتیجه، جواب کلی به شکل زیر است.
$$\large x=C_1\cos(\omega_nt)+C_2\sin(\omega_nt)+\frac{F_0}{m({\omega_n}^2-\omega^2)}\cos(\omega t)$$
جواب کلی را میتوان به صورت ساده شده زیر هم نوشت.
$$\large x=C\cos(\omega_nt-y)+\frac{F_0}{m({\omega_n}^2-\omega^2)}\cos(\omega t)$$
همانطور که میبینید، پاسخ به دست آمده، بر همکنش دو موج کسینوسی با فرکانسهای متفاوت است.
مثال
پیش از آنکه این بخش را به پایان برسانیم، به مثال زیر توجه کنید. معادلات حرکت به صورت زیر داده شدهاند.
$$\large 0.5x^{\prime\prime}+8x=10\cos(\pi t), \:\:\:x(0)=0,\:\:\:x^{\prime}(0)=0$$
با مقایسه این معادلات با معادلات حرکت، برخی پارامترها به صورت زیر قابل استخراج هستند.
$$\large \omega=\pi,\:\:\omega_n=\sqrt{\frac{8}{0.5}}=4,\:\;F_0=10,\:\:m=0.5$$
در نتیجه، جواب کلی به شکل زیر است.
$$\large x=C_1\cos(4t)+C_2\sin(4t)+\frac{20}{16-\pi^2}\cos(\pi t)$$
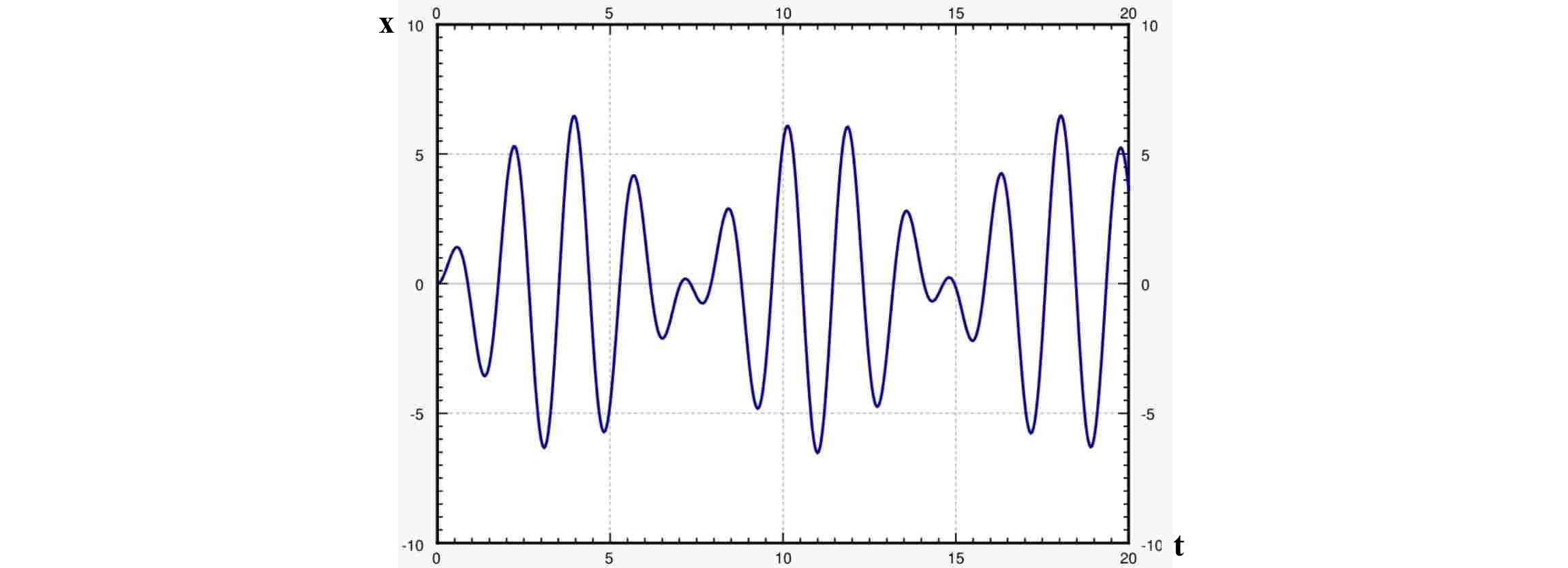
با استفاده از شرایط اولیه، مقادیر $$C_1$$ و $$C_2$$ محاسبه شده و جواب به صورت زیر ساده میشود. نمودار جواب به دست آمده، در ادامه نشان داده شده است.
$$\large x=\frac{20}{16-\pi^2}(\cos(\pi t)-\cos(4t))$$
از روابط بین سینوس و کسینوس، رابطه زیر را به یاد بیاورید.
$$\large \cos B-\cos A=2\sin(\frac{A-B}{2})\sin(\frac{A+B}{2})$$
با استفاده از این رابطه، میتوان جواب را به صورت زیر نوشت.
$$\large x=\frac{20}{16-\pi^2}(2\sin(\frac{4-\pi}{2}t)\sin(\frac{4+\pi}{2}t))$$
رابطه به دست آمده نشان میدهد که $$x$$ موجی با فرکانس زیاد است که موج دیگری با فرکانس کوچک، روی آن سوار شده است.
ارتعاش با فرکانس طبیعی
حال فرض کنیم $$\large \omega_n=\omega$$ باشد. در این حالت نمیتوانیم جواب $$\large A\cos(\omega t)$$ را امتحان کرده و پس از آن روش ضرایب نامعین را به کار ببریم. میدانیم که $$\large \cos(\omega t)$$ معادله همگن را حل میکند. بنابراین، از جواب خصوصی $$\large x_p=At\cos(\omega t)+Bt\sin(\omega t)$$ استفاده میکنیم. معادله حرکت به صورت زیر است.
$$\large x^{\prime\prime}+\omega^2x =\frac{F_0}{m}\cos(\omega t)$$
با جایگذاری $$\large x_p$$ در معادله بالا، خواهیم داشت:
$$\large 2B\omega\cos(\omega t)-2A\omega\sin(\omega t)=\frac{F_0}{m}\cos(\omega t)$$
با مقایسه دو طرف معادله بالا، $$\large A=0$$ و $$\large B=\frac{F_0}{2m\omega}$$ مشخص است. در نتیجه، جواب خصوصی و جواب کلی به صورت زیر خواهند بود.
$$\large x_p=\frac{F_0}{2m\omega}t\sin(\omega t)$$
$$\large x=C_1\cos(\omega t)+C_2\sin(\omega t)+\frac{F_0}{2m\omega}t\sin(\omega t)$$
مهمترین بخش رابطه بالا، عبارت سمت راست است. یعنی همان جواب خصوصی که ابتدا به دست آوردیم. این عبارت بین دو مقدار $$\large \frac{F_0t}{2m\omega}$$ و $$\large -\frac{F_0t}{2m\omega}$$ نوسان خواهد کرد. همان گونه که میبینید، اگر $$\large t\rightarrow\infty$$، کران بالا و پایین این حد بزرگ و بزرگتر شده و به سمت بینهایت میل میکنند. دو عبارت اول در سمت راست معادله بالا، فقط بین دو مقدار $$\large \pm\sqrt{{C_1}^2+{C_2}^2}$$ نوسان خواهد کرد که وقتی $$\large t\rightarrow\infty$$، نسبت به عبارت سمت راست، میتوان از آنها صرف نظر کرد. در نتیجه، با بزرگ شدن $$\large t$$، دامنه نوسانها بسیار بزرگ خواهد شد. این رفتار، همان رزونانس است.
محاسبه رزونانس در ارتعاش اجباری میرا
در دنیای واقعی با پدیدههایی روبرو هستیم که از معادلات ساده شده بالا تبعیت نمیکنند. در نتیجه، میرایی هم به سیستم اضافه میشود. با در نظر گرفتن میرایی، معادله حرکت به صورت زیر نوشته میشود:
$$\large mx^{\prime\prime}+cx^{\prime}+kx=F_0\cos(\omega t)$$
رابطههای زیر را قبلاً در مقاله ارتعاشات اجباری به دست آوردهایم.
$$\large p=\zeta\omega_n=\frac{c}{2m},\:\;\:\omega_n=\sqrt{\frac{k}{m}}$$
با ادغام دو رابطه اخیر، به رابطه زیر میرسیم.
$$\large x^{\prime\prime}+2px^\prime+{\omega_n}^2x=\frac{F_0}{m}\cos(\omega t)$$
ریشههای معادله مشخصه مربوط به معادله همگن، برابر با $$\large r_1, r_2=-p\pm\sqrt{p^2-{\omega_n}^2}$$ است. شکل پاسخ عمومی مربوط به معادله همگن به علامت $$\large p^2-{\omega_n}^2$$ بستگی دارد. همانطور که میدانیم این علامت، با علامت $$\large c^2-4km$$ یکسان است. در نتیجه، پاسخ عمومی را میتوان به صورت زیر نوشت.
$$\large x_c=\begin{cases}C_1e^{r_1t}+C_2e^{r_2t} & if\:\:c^2>4km\\C_1e^{pt}+C_2e^{-pt} & if\:\:c^2=4km\\e^{-pt}(C_1\cos(\omega_1t)+C_2\sin(\omega_1t)) & if\:\:c^2<4km\end{cases}$$
در رابطه بالا، $$\large \omega_1=\sqrt{{\omega_n}^2-p^2}$$ است. همانطور که مشاهده میشود، در هر شرایطی اگر $$\large t\rightarrow\infty$$ آنگاه $$\large x_c(t)\rightarrow0$$ اتفاق میافتد. جواب خصوصی $$\large x_p=A\cos(\omega t)+B\sin(\omega t)$$ را میتوان به صورت زیر محاسبه کرد.
$$\large (({\omega_n}^2-\omega^2)B - 2\omega p A)\sin(\omega t) + (({\omega_n}^2-\omega^2)A+2\omega pB)\cos(\omega t)=\frac{F_0}{m}\cos(\omega t)$$
با مقایسه دو طرف رابطه، نتایج زیر به دست میآید.
$$\large A=\frac{({\omega_n}^2-\omega^2)F_0}{m(2\omega p)^2+m({\omega_n}^2-\omega^2)^2}\\~\\
\large B=\frac{2\omega pF_0}{m(2\omega p)^2+m({\omega_n}^2-\omega^2)^2}$$
اگر $$C$$ را به صورت $$\large C=\sqrt{A^2+B^2}$$ فرض کنیم، جواب خصوصی به شکل زیر به دست میآید.
$$\large C=\frac{F_0}{m\sqrt{(2\omega p)^2+({\omega_n}^2-\omega^2)^2}}\\~\\
\large x_p=\frac{({\omega_n}^2-\omega^2)F_0}{m(2\omega p)^2+m({\omega_n^2}-\omega^2)^2}\cos(\omega t)+\frac{2\omega pF_0}{m(2\omega p)^2+m({\omega_n^2}-\omega^2)^2}\sin(\omega t)$$
میتوانیم تغییر فاز $$\large \gamma$$ را از رابطه زیر محاسبه کنیم (در حالتی که $$\large \omega\neq\omega_n$$).
$$\large \tan\gamma=\frac{B}{A}=\frac{2\omega p}{{\omega_n}^2-\omega^2}$$
در نتیجه، جواب خصوصی به صورت زیر ساده میشود.
$$\large x_p=\frac{F_0}{m\sqrt{(2\omega p)^2+({\omega_n}^2-\omega^2)^2}}\cos(\omega t-\gamma)$$
حالت گذرا و حالت پایدار
حال اگر $$\large \omega=\omega_n$$ باشد، حالت زیر رخ میدهد.
$$\large A=0, \:\:\:B=C=\frac{F_0}{2m\omega p}, \:\:\: \gamma=\frac{\pi}{2}$$
نیازی نیست که رابطه به دست آمده را به خاطر بسپارید. زیرا با تغییر تابع $$\large F$$ جواب به دست آمده نیز تغییر خواهد کرد. ولی لازم است روند به دست آوردن جواب را به خوبی یاد بگیرید. جواب کلی این مسأله به شکل زیر است.
$$\large x=x_c+x_p=x_{tr}+x_{sp}$$
همانطور که میدانیم هنگامی که $$\large t \rightarrow \infty$$، آنگاه $$\large x_c=x_{tr}$$ هم به صفر میل خواهد کرد. در نتیجه، برای مقادیر بزرگ $$t$$، میتوان از تأثیر $$\large x_{tr}$$ صرف نظر کرد و فقط $$\large x_{sp}$$ دیده خواهد شد. توجه کنید که بخش $$\large x_{sp}$$ دارای هیچ ثابت دلخواهی نیست و شرایط اولیه فقط روی $$\large x_{tr}$$ تأثیر میگذارند. در نتیجه، پس از گذشت یک دوره زمانی، تأثیر شرایط اولیه قابل چشمپوشی خواهد بود. بنابراین از پاسخ حالت گذرا صرف نظر میکنیم و روی پاسخ حالت پایدار متمرکز خواهیم شد. شکل زیر را در نظر بگیرید. در نمودارهای مختلفی که مشاهده میکنید، ضرایب $$\large k$$، $$\large m$$، $$\large F_0$$، $$\large c$$ و $$\large \omega$$ یکی است و تفاوت فقط در شرایط اولیه است.
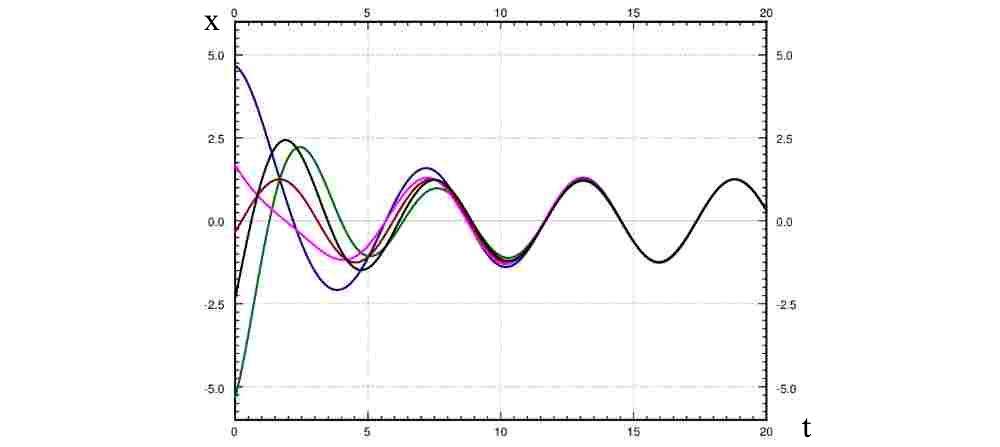
به این نکته توجه کنید که سرعت میل کردن $$\large x_{tr}$$ به صفر، به $$\large p$$ بستگی دارد. هرچه $$\large p$$ بزرگتر باشد، $$\large x_{tr}$$ زودتر به صفر میل خواهد کرد. در نتیجه هرچه میرایی سیستم کوچکتر باشد، ناحیه گذرا طولانیتر خواهد بود. در بخش قبلی دیدیم که برای ارتعاش نامیرا، شرایط اولیه، رفتار سیستم را در تمام زمانها تحت تأثیر قرار میدهند. یعنی طول مدت حالت گذرا، بینهایت است.
محاسبه دامنه رزونانس
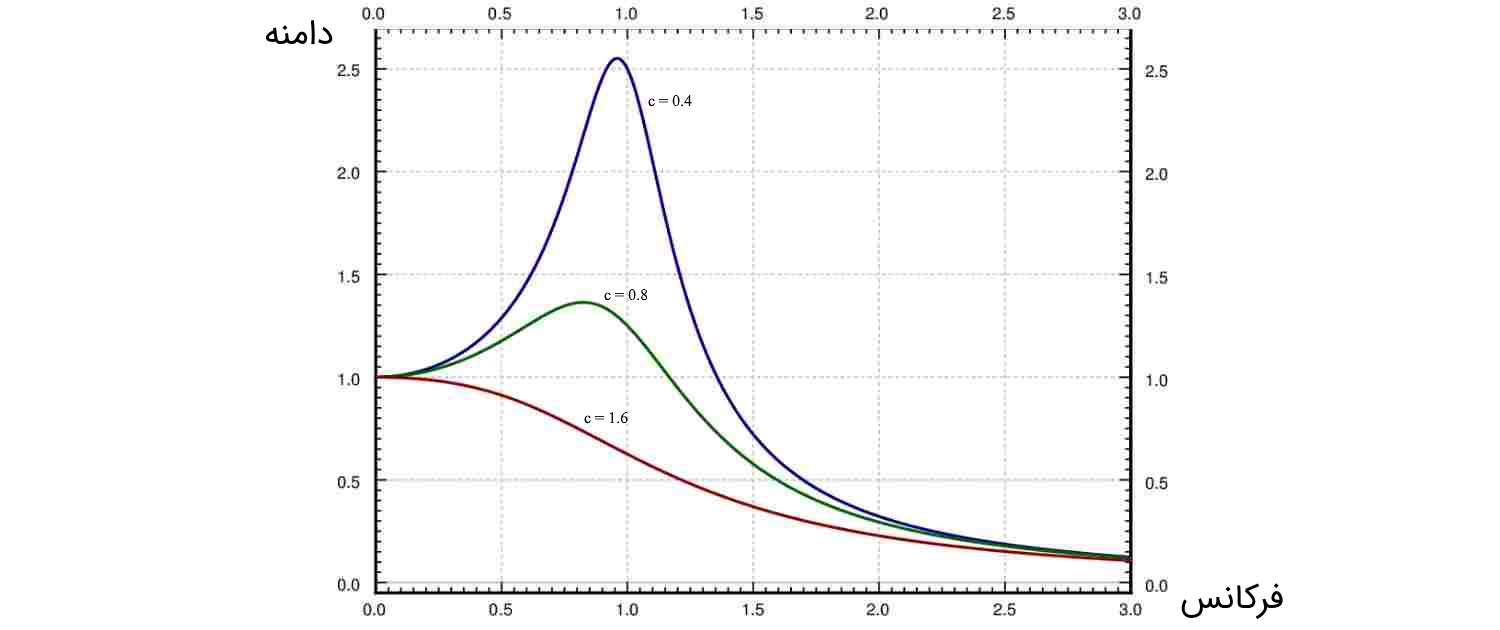
حال میخواهیم ببینیم در ارتعاش میرا، مقدار بیشینه دامنه در حالت پایدار چقدر است. دامنه در حالت پایدار $$\large x_{sp}$$ را با $$C$$ نشان میدهیم. اگر نمودار $$C$$ برحسب $$\omega$$ را رسم کنیم، میتوانیم محل وقوع این دامنه را بیابیم. فرکانسی که بیشیه دامنه در آن اتفاق میافتد را فرکانس رزونانس و دامنه آن را دامنه رزونانس مینامیم. در شکل زیر نمودار دامنه برحسب فرکانس برای سه ضریب میرایی مختلف رسم شده است. همانطور که مشاهده میکنید هرچه میرایی کمتر باشد، دامنه رزونانس بزرگتر میشود و هنگامی که میرایی بزرگ باشد، رزونانس به کلی از بین میرود.
برای پیدا کردن نقطه ماکسیمم، از تابع $$C(\omega)$$ مشتق میگیریم.
$$\large C^\prime(\omega)=\frac{-4\omega(2p^2+\omega^2-{\omega_n}^2)F_0}{m((2\omega p)^2+({\omega_n}^2-\omega^2))^{3/2}}$$
رابطه بالا در دو حالت میتواند صفر باشد، یکی هنگامی که $$\large \omega=0$$ و یکی هم زمانی که عبارت $$\large 2p^2+\omega^2-{\omega_n}^2$$ برابر با صفر باشد. با حل این معادله، $$\large \omega$$ به صورت زیر محاسبه میشود.
$$\large \omega=\sqrt{{\omega_n}^2-2p^2}$$
میتوان نشان داد، زمانی که عبارت $$\large {\omega_n}^2-2p^2$$ مثبت است، فرکانس رزونانس با $$\large \sqrt{{\omega_n}^2-2p^2}$$ برابر است و نمودار $$\large C(\omega)$$ به مقدار بیشینه میرسد. اگر بیشینه نمودار در نقطه $$\large \omega = 0$$ رخ دهد، هیچ رزونانسی اتفاق نخواهد افتاد. در این حالت با کوچک شدن فرکانس نیرو، دامنه بزرگتر خواهد شد.
زمانی که رزونانس اتفاق میافتد، فرکانس آن از $$\large \omega_n$$ کوچکتر است. هرچه ضریب میرایی $$\large c$$ کوچکتر باشد، فرکانس رزونانس به سمت $$\large \omega_n$$ میل میکند. بنابراین، هنگامی که میرایی خیلی ناچیز باشد، فرکانس رزونانس تقریباً با فرکانس طبیعی برابر است.
اگر به مباحث مرتبط در زمینه کنترل، مکانیک و ارتعاشات علاقهمند هستید، آموزشهای زیر به شما پیشنهاد میشوند:
- ژیروسکوپ – از صفر تا صد
- ارتعاشات مکانیکی — بخش اول: اصول و مفاهیم
- ارتعاشات مکانیکی — بخش دوم: ارتعاشات اجباری
- ارتعاشات مکانیکی — بخش سوم: سیستمهای دو درجه آزادی
^^










با سلام، لطفا در خصوص هارمونیکهای رزونانسی یک سازه یا جسم، همچنین تئوری و مفاهیم superharmonic resonance و subharmonic resonance توضیح ارایه فرمایید
با تشکر از تیم آموزشی فرادرس
پدیده رزونانس در مبحث برق هم وجود دارد . در واقع بخش ذاتی سیستم هست
ممنون می شوم مطالب مرتبط به رزونانس در برق را باز بان ساده بیان کنید.
سلام ميشه توضيح بديد نقش جعبه هاى رزونانس در آزمايش دياپازون چيه؟ ممنون