نمایش فضای حالت و تابع تبدیل — به زبان ساده (+ دانلود فیلم آموزش گام به گام)

اولین گام در فرایند طراحی سیستم‌های کنترل، تشکیل مدل‌های ریاضی مناسب برای سیستمی است که می‌خواهیم آن را کنترل کنیم. این مدل‌ها را می‌توان از قوانین فیزیکی یا داده‌های آزمایش به‌دست آورد. در این آموزش، نمایش فضای حالت و تابع تبدیل مدل سیستم‌های دینامیکی را معرفی خواهیم کرد.

سیستم‌های دینامیکی

«سیستم‌های دینامیکی» (Dynamic Systems)، سیستم‌هایی هستند که با توجه به یک قانون ثابت، نسبت به زمان تغییر می‌کنند. در بسیاری از سیستم‌های فیزیکی، این قانون را می‌توان با یک مجموعه معادلات دیفرانسیل مرتبه اول بیان کرد:

فیلم آموزش کنترل مدرن و پیاده سازی در متلب MATLAB در فرادرس

کلیک کنید

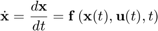
در معادله بالا، $$x(t)$$ بردار حالت نامیده می‌شود و مجموعه‌ای از متغیرهای تشکیل دهنده دینامیک سیستم در زمان $$t$$ است. $$u(t)$$ بردار ورودی‌های خارجی یا بیرونی سیستم در زمان $$t$$ بوده و $$f$$ تابعی (شاید غیرخطی) است که مشتق زمانی (نرخ تغییرات) بردار حالت را مشخص می‌کند.

بردار حالت $$x(t_1)$$ را در هر زمان آینده می‌توان به‌صورت دقیق و با داشتن مقدار اولیه $$x(t_0)$$ و ورودی‌های گذشته به‌کمک انتگرال از $$t_0$$ تا $$t_1$$ معادله (1) تعیین کرد.

اگرچه متغیرهای حالت، منحصربه‌فرد نیستند، اما باید تعداد حداقل $$n$$ متغیر وجود داشته باشد که بتوان با آن‌ها «حالت» سیستم را بررسی و رفتار آینده آن را پیش‌بینی کرد. $$n$$، مرتبه سیستم (System Order) نامیده می‌شود و بُعد فضای حالت را مشخص می‌کند. مرتبه سیستم، معمولاً با تعداد عناصر ذخیره‌کننده انرژی در سیستم متناظر است.

رابطه (۱) بسیار عمومی است و با آن می‌توان سیستم‌های مختلفی را توصیف کرد. اما گاهی تحلیل این معادله بسیار دشوار است. دو ساده‌سازی متداول برای غلبه بر این دشواری وجود دارد. اولی این است که تابع $$f$$ به زمان بستگی نداشته باشد؛ یعنی $$\dot{x}=f(x,u)$$، که به آن تغییرناپذیر با زمان (Time Invariant) می‌گویند. این فرض، اغلب منطقی است، زیرا قوانین فیزیکی معمولاً به زمان وابسته نیستند. در سیستم‌های تغییرناپذیر با زمان، پارامترها یا ضرایب تابع $$f$$ ثابت هستند. البته متغیرهای حالت و ورودی‌های کنترل ممکن است وابسته به زمان باشند.

دومین فرض متداول، خطی بودن سیستم است. در واقعیت، تقریباً هر سیستم فیزیکی غیرخطی است. به عبارت دیگر، $$f$$ معمولاً یک تابع پیچیده از متغیرهای حالت و ورودی‌ها است. خوشبختانه، دینامیک اغلب سیستم‌ها، در یک محدوده کاری کوچک (مشابه خط مماس بر یک منحنی)، خطی است. در نتیجه، معادلات دیفرانسیل مرتبه اول سیستم را می‌توان به‌فرم معادله ماتریسی $$\dot{x}=Ax+Bu$$ نوشت.

تا قبل از ظهور و گسترش کامپیوترهای دیجیتال، فقط تحلیل سیستم‌های خطی تغییر ناپذیر با زمان (LTI) ممکن بود. در نتیجه، اغلب نتایج نظریه کنترل بر اساس این فرضیات بنا شده‌اند. خوشبختانه، اثبات شده که این نتایج مؤثر بوده و بسیاری از چالش‌های بزرگ مهندسی با استفاده از تکنیک‌های مربوط به سیستم‌های LTI حل شده است.

نمایش فضای حالت

نمایش «فضای حالت» (State Space) استاندارد سیستم‌های LTI به صورت زیر است:

فیلم آموزش کنترل مدرن – حل ۱۰۰ مساله در فرادرس

کلیک کنید

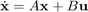
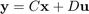
که در آن، $$x$$ بردار متغیرهای حالت ($$n\times 1$$)، $$\dot{x}$$ مشتق زمانی بردار حالت ($$n\times 1$$)، $$u$$ بردار ورودی یا کنترل ($$p \times 1$$)، $$y$$ بردار خروجی ($$q\times 1$$)، $$A$$ ماتریس سیستم ($$n \times n$$)، $$B$$ ماتریس ورودی ($$p\times 1$$)، $$C$$ ماتریس خروجی ($$q \times n$$) و $$D$$ ماتریس پیش‌خور ($$q \times p$$) است.

معادله خروجی (۳)، معادله‌ای مهم است، زیرا گاهی متغیرهای حالت را نمی‌توان مستقیماً مشاهده کرد. ماتریس خروجی $$C$$ تعیین می‌کند که کدام یک متغیرهای حالت برای استفاده کنترل‌کننده در دسترس هستند. همچنین، در مواردی خروجی‌ها مستقیماً با ورودی‌ها ارتباط ندارند و فقط با متغیرهای حالت رابطه دارند که در این صورت، ماتریس $$D$$‌ برابر با صفر است.

نمایش فضای حالت، نمایش حوزه زمان نیز نامیده می‌شود و با آن می‌توان سیستم‌های چندورودی-چندخروجی (MIMO)، سیستم‌های با شرایط اولیه غیرصفر و سیستم‌‌های غیرخطی را نمایش داد. بنابراین، می‌توان گفت نمایش فضای حالت، به طور گسترده‌ای در نظریه کنترل مدرن استفاده می‌شود.

نمایش تابع تبدیل

سیستم‌های LTI یک ویژگی بسیار مهم دارند و آن این است که اگر ورودی سیستم، سینوسی باشد، خروجی نیز با همان فرکانس سینوسی است، اما ممکن است دامنه و فاز آن متفاوت از ورودی باشد. این اختلاف دامنه و فاز، تابعی از فرکانس هستند و به عنوان پاسخ فرکانسی سیستم شناخته می‌شوند.

فیلم آموزش سیستم های کنترل خطی در فرادرس

کلیک کنید

با استفاده از تبدیل لاپلاس می‌توان نمایش حوزه زمان را به نمایش ورودی/خروجی حوزه فرکانس تبدیل کرد که با نام «تابع تبدیل» (Transfer Function)‌ شناخته می‌شود. با تبدیل نمایش حوزه زمان به نمایش حوزه فرکانس، در حقیقت معادلات دیفرانسیل را به یک معادله جبری تبدیل می‌کنیم که تحلیل آن بسیار ساده‌تر است.

تبدیل لاپلاس تابع زمانی $$f(t)$$ به‌صورت زیر تعریف می‌شود:

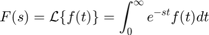
که در آن، پارامتر $$s=\sigma + j \omega$$ یک متغیر فرکانسی مختلط است. در عمل، بسیار کم پیش می‌آید که تبدیل لاپلاس را مستقیماً محاسبه کنیم و اغلب از جدول تبدیلات لاپلاس برای یافتن آن‌ها کمک می‌گیریم.

تبدیل لاپلاس مشتق nاُم یک تابع، از روابط مهمی است که با آن سروکار داریم:

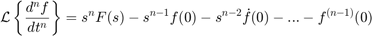
از روش‌های حوزه فرکانس، معمولاً برای تحلیل سیستم‌های تک‌ورودی-تک‌خروجی (SISO) استفاده می‌شود. سیستم زیر را در نظر بگیرید:

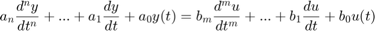
تبدیل لاپلاس معادله بالا به‌صورت زیر است:

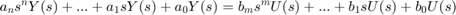
که در آن، $$Y(s)$$ و $$U(s)$$ به‌ترتیب، تبدیلات لاپلاس $$u(t)$$ و $$y(t)$$ هستند. هنگام یافتن توابع تبدیل، فرض مي‌کنیم شرایط اولیه $$y(0)$$، $$\dot{y}(0)$$، $$u(0)$$ و... صفر هستند. بنابراین، تابع تبدیل از ورودی $$U(s)$$ به خروجی $$Y(s)$$ به‌صورت زیر خواهد بود:

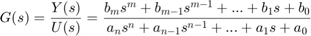
با نوشتن صورت و مخرج تابع تبدیل به‌صورت صفر-قطب-بهره می‌توانیم آن را بهتر تحلیل کنیم:

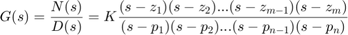
صفرهای ($$z_1,...,z_m$$) تابع تبدیل، ریشه‌های چندجمله‌ای صورت هستند؛ یعنی مقادیری از $$s$$ که به‌ازای آن‌ها $$N(s)=0$$ است. قطب‌های ($$p_1,...,p_n$$) تابع تبدیل، ریشه‌های چندجمله‌ای مخرج هستند؛ یعنی مقادیری از $$s$$ که به‌ازای آن‌ها $$D(s)=0$$ است. صفرها و قطب‌های تابع تبدیل، ممکن است اعداد مختلط (شامل بخش حقیقی و موهومی) باشند. بهره سیستم برابر است با $$K=b_0/a_0$$.

با استفاده از فرمول زیر می‌توان تابع تبدیل را مستقیماً از نمایش فضای حالت به دست آورد:

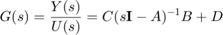
در آموزش بعدی، مثال‌هایی از مدل‌سازی سیستم‌های دینامیکی را با کمک نرم‌افزار متلب ارائه خواهیم کرد.

^^