تبدیل لاپلاس و محاسبه آن — به زبان ساده

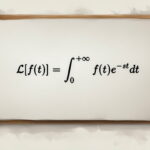
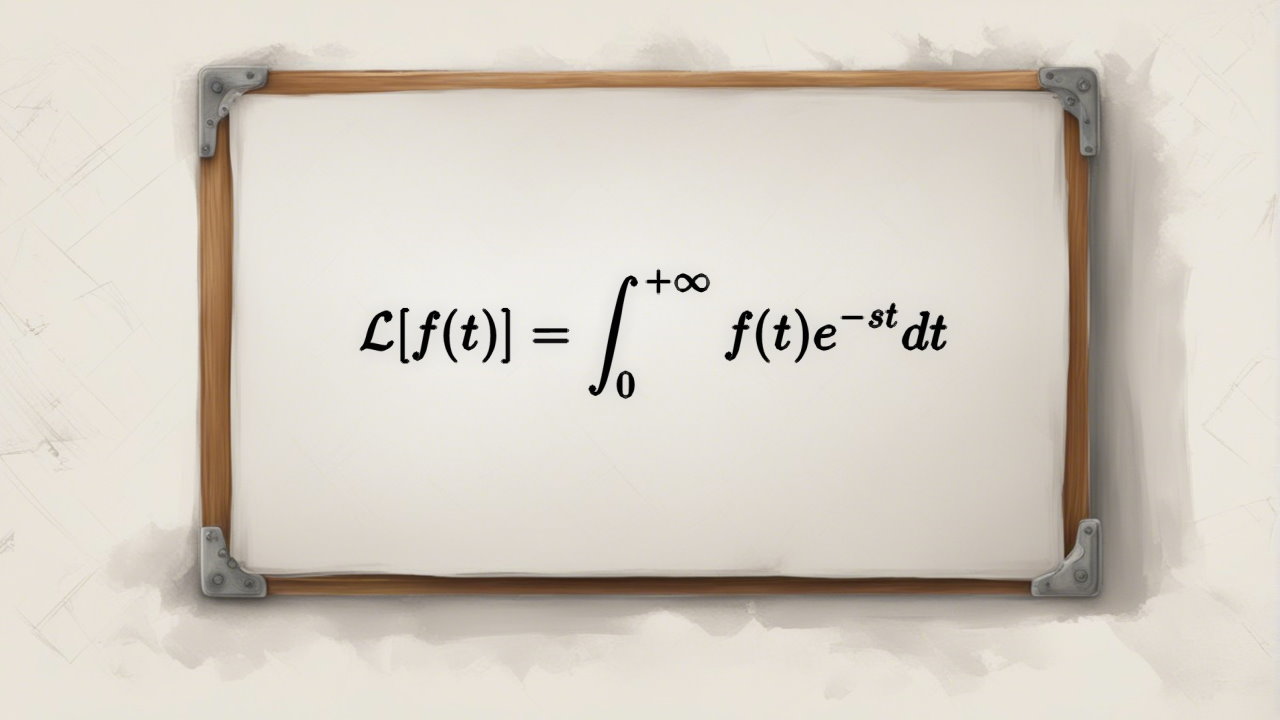
پیش‌تر در بلاگ فرادرس در مورد معادلات دیفرانسیل مرتبه اول، دوم و بعضی از روش‌های مرسوم حل آن‌ها صحبت کردیم. بدیهی است که همواره نمی‌توان با استفاده از روش‌های مذکور معادلات را حل کرد. در این قسمت ابزاری قدرتمند را معرفی می‌کنیم که در حل معادلات دیفرانسیل بسیار پرکاربرد است. این ابزار «تبدیل لاپلاس» (Laplace Transform) است. در این مطلب در ابتدا این تبدیل را معرفی کرده و پس از آن تکنیک‌هایی را در مورد حل آن‌ها معرفی خواهیم کرد. البته در بخشی جدا، در آینده در مورد کاربرد این مفهوم در حل معادلات دیفرانسیل بحث خواهیم کرد.

تعریف تبدیل لاپلاس

(f(t را به‌ عنوان تابعی از متغیر مستقل t در نظر بگیرید. تبدیل لاپلاس (f(t برابر است با تابعی از متغیر جدید s که در حالت کلی می‌تواند مختلط نیز باشد. تبدیل لاپلاس تابع (f(t را با استفاده از فرمول زیر بدست می‌آوریم.

فیلم آموزش معادلات دیفرانسیل با رویکرد حل مساله و تست کنکور ارشد در فرادرس

کلیک کنید

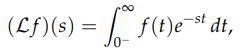
جهت استفاده از فرمول بالا توجه به نکات زیر ضروری است:

• لاپلاس برای مقادیری از s قابل قبول است که به ازای ‌‌آن‌ها سمت راست معادله بالا همگرا شود.
• متغیر s می‌تواند مختلط نیز باشد.
• حدود انتگرال نشان می‌دهند که تبدیل لاپلاس، فقط عبارت زیر انتگرال را در بازه (∞+,^-0) مورد توجه قرار می‌دهد.

نماد‌گذاری (F(s

معمولا نوشتن (Lf(s مشکل است، بنابراین مرسوم است که تابع لاپلاس را به‌صورت مستقیم نشان می‌دهند. این نماد‌ها در زیر نشان داده شده‌اند.

اگر تابعی که می‌خواهیم از آن لاپلاس بگیریم، اسم نداشته باشد، می‌توان مستقیما خود تابع را تحت نماد لاپلاس قرار داد. برای نمونه لاپلاس تابع t² را می‌توان به صورت (L(t²)(s یا (L(t² نشان داد.

در بعضی از موارد نیاز به تغییر تابع (f(t است. در این موارد تابع تغییر داده شده را نیز تحت اوپراتو لاپلاس قرار می‌دهیم. برای نمونه اگر بخواهیم لاپلاس تابع (f(t را در حالتی بیابیم که به اندازه a جابجا شده، از نماد ((L(f(t-a استفاده می‌کنیم.

می‌توان گفت که در برخی از موارد، پرانتز‌های به‌کار رفته در نماد لاپلاس کم یا زیاد می‌شوند. در حقیقت تمامی نماد‌های به‌کار رفته در پایین، معادل یکدیگر هستند.

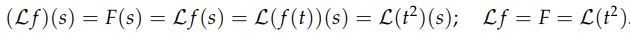
مثال‌های اولیه

در حالت کلی، جهت بدست آوردن لاپلاس یک تابع، بایستی از رابطه ۱ استفاده کرد. البته در ادامه قوانینی را نیز بیان خواهیم کرد که با استفاده از آن‌ها می‌توان لاپلاس توابع پیچیده‌تر را نیز یافت.

فیلم آموزش معادلات دیفرانسیل + حل سوالات کنکور کارشناسی ارشد در فرادرس

کلیک کنید

مثال ۱

فرض کنید هدف ما بدست آوردن لاپلاس تابع f(t)=1 است. بنابراین با استفاده از رابطه ۱ داریم:

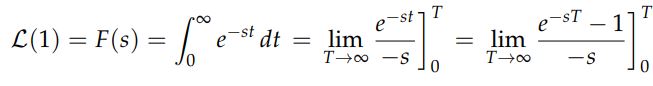
همان‌طور که در رابطه بالا نیز می‌بینید، پاسخ این حد بسته به این‌که مقدار s مثبت یا منفی باشد، متفاوت خواهد بود. در حقیقت پاسخ آن به ازای دو مقدار مثبت و منفی s، بصورت زیر است:

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

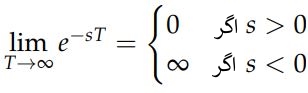
در نتیجه لاپلاس تابع ثابت f(t)=1 برابر است با:

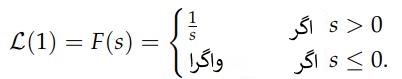
مثال ۲

در این مثال قصد داریم تا لاپلاس تابع e^at را بیابیم. با استفاده از تعریف داریم:

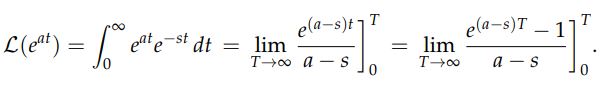
مشابه با مثال قبل، در این حالت نیز تابعِ لاپلاس محاسبه شده، وابسته به مقدار s است. در حقیقت می‌توان گفت:

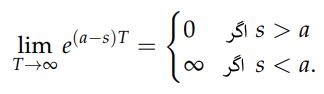
در نتیجه:

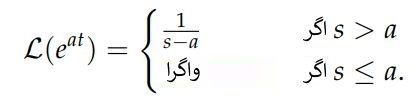
با توجه به دو مثال ۱ و ۲ می‌توان گفت:

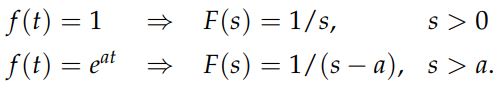
تکنیک‌های محاسبه لاپلاس

از نظر مفهومی لاپلاس یک تابع را بایستی با استفاده از رابطه ۱ بدست آورد. اما جهت سادگی حل مسائل، تکنیک‌هایی نیز وجود دارد که می‌توان با استفاده از آن‌‌ها لاپلاس را محاسبه کرد. برای نمونه لاپلاس تابع t برابر است با:

فیلم آموزش معادلات دیفرانسیل با میپل Maple در فرادرس

کلیک کنید

به همین صورت لاپلاس تابع t² به شکل زیر بدست می‌آید.

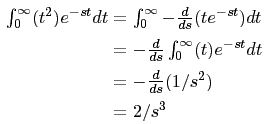
در حقیقت لاپلاس تابع tⁿ را می‌توان با رابطه زیر بدست آورد.

$$L(t^n)= {n! \over s^{n+1}}$$

قوانین مشابه بسیاری در مورد محاسبه لاپلاس وجود دارد. در ادامه قصد داریم تا لاپلاس تابع sin ωt را بیابیم. بر مبنای رابطه ۱، لاپلاس تابع مذکور برابر است با:

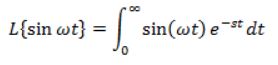
به منظور استفاده از روش انتگرال‌گیری جزء به جزء بایستی فرض زیر را انجام داد.

در نتیجه با فرض توابع در نظر گرفته شده در بالا داریم:

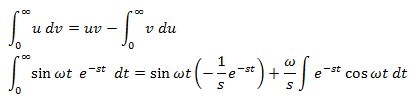
در این مرحله دوباره از انتگرال جزء به جزء استفاده می‌کنیم. توابع جدید u و v را به‌صورت زیر در نظر می‌گیریم:

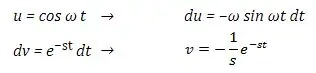
با این فرضیات نهایتا لاپلاس تابع sin ωt برابر می‌شود با:

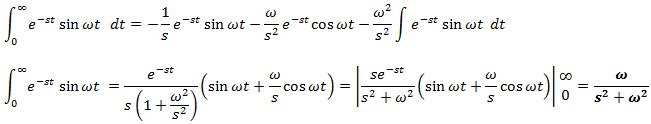
دقیقا با استفاده از همین روش لاپلاس تابع Acos ωt برابر با تابع زیر بدست خواهد آمد.

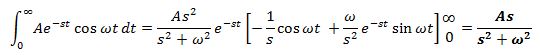
یکی از توابعی که لاپلاس آن در مسائل مهندسی بسیار پرکاربرد است، لاپلاس مشتق تابع است؛ بنابراین فرض کنید می‌خواهیم لاپلاسِ تابع f(t)=df(t)/dt را بیابیم. در ابتدا فرض شده که لاپلاس تابع (f(t معلوم و برابر با تابع زیر است.

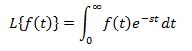
جهت محاسبه این لاپلاس نیز از مفهوم انتگرال‌گیری جزء به جزء استفاده می‌شود. در حقیقت در این مسئله (u=f(t و dv=e^-stdt فرض می‌شود. در حقیقت:

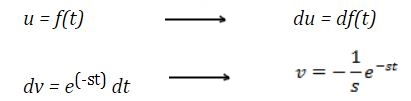
با اعمال انتگرال‌گیری جزء به جزء داریم:

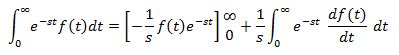
در رابطه بالا عبارت اول، مقدار تابع در صفر و عبارت دوم لاپلاس تابع (f(t را نشان می‌دهد. بنابراین:

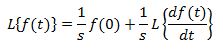
در نتیجه نهایتا لاپلاس مشتق (f(t برابر می‌شود با:

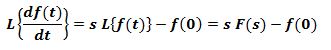
در بالا چند نمونه لاپلاس را بدست آوردیم؛ در جدول زیر لاپلاس توابع شناخته شده ذکر شده که جهت محاسبه سریع‌تر مسائل می‌توانید از آن‌ها استفاده کنید.

البته جهت استفاده از لاپلاس قوانینی نیز وجود دارند که به‌منظور محاسبه لاپلاس می‌توانند مفید باشند. برای نمونه فرض کنید با داشتن لاپلاس تابع (f(t، می‌خواهیم لاپلاس (f(t-a را بیابیم. از تعریف لاپلاس می‌دانیم که لاپلاس تابع (f(t-a برابر است با:

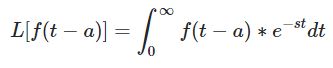
با استفاده از تغییر متغیر u=t-a و نوشتن آن به‌صورت t=u+a داریم:

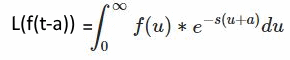
بدیهی است که پاسخ انتگرال بالا برابر با تابع زیر است:

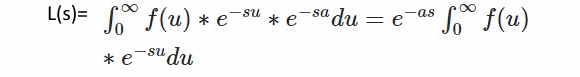
در نتیجه لاپلاس این تابع برابر است با:

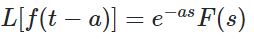
با استفاده از این قانون نیاز نیست جهت محاسبه لاپلاس، همواره از تعریف استفاده کرد.

قوانین بسیاری در لاپلاس‌ها وجود دارند که می‌توان از آن‌ها جهت محاسبه راحت‌تر لاپلاس توابع مختلف استفاده کرد. در جدول زیر برخی از مهم‌ترین این قوانین ذکر شده است.

برای نمونه فرض کنید می‌خواهیم تبدیل لاپلاس تابع $$t^2sin(2t)$$ بیابیم. یکی از روابط ارائه شده در جدول بالا به‌صورت زیر است.

L(tⁿf(t))=(-1)ⁿFⁿ(s)

با فرض این‌که تابع H، نشان دهنده تبدیل تابع باشد، داریم:

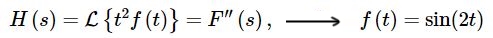
بنابراین پاسخ لاپلاسِ مدنظر برابر با مشتق دوم تابع $$\Large {2 \over {s^2+4}}$$ است. در نتیجه با محاسبه مشتق دوم تابع مذکور داریم:

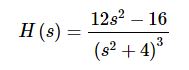
البته همین مثال را می‌توانستیم با فرض tsin 2t به عنوان تابع اصلی و با یک‌ بار مشتق‌گیری از لاپلاس مربوطه آن، حل کنیم. به‌منظور تسلط کامل‌تر به مبحث لاپلاس، آموزش ویدئویی قرار گرفته در این لینک توصیه می‌شود. در بخش‌های آینده در مورد مفاهیم لاپلاس معکوس صحبت خواهیم کرد. لاپلاس معکوس یکی از مباحث کاربردی در حل معادلات دیفرانسیل است.