تقسیم ولتاژ در مدار – به زبان ساده

در آموزش‌های پیشین مجله فرادرس، با مهم‌ترین ابزارهای تحلیل مدارهای الکتریکی از قبیل قانون اهم، قضایای تونن و نورتن، قوانین کیرشهف، تحلیل مش و گره، تبدیل ستاره-مثلث و تبدیل منابع آشنا شدیم. در این آموزش، قاعده تقسیم ولتاژ را بیان می‌کنیم که با استفاده از آن می‌توانیم ولتاژ هر مقاومت سری را در یک مرحله و بدون نیاز به محاسبه جریان به دست آوریم.

فرمول تقسیم ولتاژ

همان‌طور که می‌دانیم، افت ولتاژ دو سر هر مقاومت سری در مدار، با اندازه آن مقاومت متناسب است. طبق قانون ولتاژ کیرشهف (KVL)، مجموع افت ولتاژهای همه مقاومت‌ها باید برابر با اندازه ولتاژ منبع ولتاژ اعمالی باشد.

مدار شکل ۱ را در نظر بگیرید.

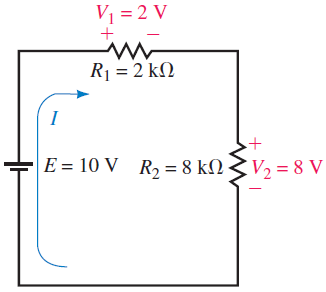
همان‌طور که می‌بینیم، مقاومت کل $$R _ T = 10 \, \text{k}\Omega$$ است و جریان $$I = 1\, \text{mA}$$ از مدار می‌گذرد. با توجه به قانون اهم، افت ولتاژ دو سر مقاومت $$R _ 1$$ برابر با $$V _ 1 = 2 \, \text{V}$$ است. از آنجایی که مقاومت $$R _ 2$$ چهار برابر $$R _ 1$$ است، افت ولتاژ‌ دو سر آن نیز چهار برابر، یعنی $$V _ 2 = 8 \, \text{V}$$ است.

همچنین، می‌بینیم که مجموع افت ولتاژهای مقاومت‌ها دقیقاً برابر با ولتاژ منبع است:‌

$$\large E = 10 \, \text{V} = 2 \, \text{V} + 8 \, \text{V}$$

با استفاده از قاعده تقسیم ولتاژ می‌توانیم ولتاژ هر مقاومت سری را در یک مرحله و بدون نیاز به محاسبه جریان به دست آوریم. همان‌طور که می‌دانیم، برای هر تعداد مقاومت سری، جریان مدار با استفاده از قانون اهم و به صورت زیر تعیین می‌شود:

$$\large I = \frac { E } { R _ T } \;\;\;\;\;\;\;\;\;\; (1)$$

برای دو مقاومت شکل ۱، مقاومت کل برابر است با:

$$\large R _ T = R _ 1 + R _ 2$$

با اعمال قانون اهم، افت ولتاژ دو سر هر مقاومت را می‌توان به صورت زیر محاسبه کرد:

$$\large V _ x = I R _ x$$

با قرار دادن رابطه (۱) در رابطه اخیر، قانون تقسیم ولتاژ برای دو مقاومت با معادله ساده زیر به دست می‌آید:‌

$$\large V _ x = \frac { R _ x } { R _ T } E = \frac {R _ x } { R _ 1 + R _ 2 } E$$

در حالت کلی، برای هر تعداد دلخواه مقاومت، افت ولتاژ هر کدام از مقاومت‌ها را می‌توان با استفاده از فرمول ساده زیر به دست آورد:

$$\large V _ x = \frac { R _ x } { R _ T } E \;\;\;\;\;\;\;\;\;\; (2 )$$

رابطه (۲)، همان فرمول کلی تقسیم ولتاژ‌ است که در تحلیل سریع مدار بسیار مفید خواهد بود.

مثال‌ها

در ادامه، دو مثال از کاربرد رابطه تقسیم ولتاژ را بیان می‌کنیم.

فیلم آموزش مدارهای الکتریکی ۱ – جامع و کاربردی در فرادرس

کلیک کنید

مثال 1

با استفاده از قانون تقسیم ولتاژ، ولتاژ دو سر هر یک از مقاومت‌های مدار شکل زیر را تعیین کنید.

حل:

$$\large \begin {align*} R _ T & = 6 \, \Omega + 12 \, \Omega + 7 \, \Omega = 25\, \Omega \\ V _ 1 & = \left ( \frac { 6 \, \Omega } { 25\, \Omega } \right ) ( 18\, \text{V} ) = 4.32 \, \text {V} \\ V _ 2 & = \left ( \frac { 12 \, \Omega } { 25\, \Omega } \right ) ( 18\, \text{V} ) = 8.64 \, \text {V} \\ V _ 3 & = \left ( \frac { 7 \, \Omega } { 25\, \Omega } \right ) ( 18\, \text{V} ) = 5.04 \, \text {V} \end {align*}$$

افت ولتاژ کل نیز برابر است با:

$$\large V _ T = 4.32 \, \text {V} + 8.64 \, \text {V} + 5.04 \, \text {V} = 18.0 \, \text{V} = 18\, \text{V} = E$$

مثال ۲

با استفاده از قانون تقسیم ولتاژ، ولتاژ‌ هریک از مقاومت‌های مدار شکل زیر را محاسبه کنید.

حل:

$$\large \begin {align*} R _ T & = 2 \, \Omega + 1,000,000 \, \Omega = 1, 000 , 002 \, \Omega \\ V _ 1 & = \left ( \frac { 2 \, \Omega } { 1,000,002 \, \Omega } \right ) ( 20 \, \text {V} ) \approx 40\, \mu \text {V} \\ V _ 2 & = \left ( \frac { 1 \, \text{M}\Omega } { 1,000,002 \, \Omega } \right ) ( 20 \, \text {V} ) =19.9986 \, \text{V} \approx 20\, \text {V} \end {align*}$$

مثال اخیر دو نکته مهم دارد که معمولاً در مدارهای الکترونیکی با آن مواجه می‌شویم. اگر اندازه یک مقاومت سریِ تنها نسبت به اندازه سایر مقاومت‌های سری بسیار بزرگ باشد، آن‌گاه افت ولتاژ‌ آن مقاومت عملاً برابر با کل ولتاژ اعمالی خواهد بود. از سوی دیگر، اگر اندازه یک مقاومت از مقاومت‌های سری بسیار کوچک باشد، آن‌گاه افت ولتاژ آن مقاومت عملاً برابر با صفر است.

به عنوان یک قاعده کلی، اگر اندازه یک مقاومت سری بیش از ۱۰۰ برابر بزرگتر از اندازه سایر مقاومت‌(های) سری با خود باشد، آن‌گاه می‌توان از اثر مقاومت‌(های) کوچکتر صرف‌نظر کرد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مدار سه فاز — از صفر تا صد
• منبع تغذیه سوئیچینگ — به زبان ساده
• ال ای دی (LED) چیست؟ — به زبان ساده
• پتانسیومتر — از صفر تا صد

^^